弹簧储能式发电系统涡卷弹簧的设计与分析

杨俊茹,任保飞,孙绍帅,赵 姗

（山东科技大学机械电子工程学院,山东 青岛266590）

1 引言

当前的能源危机和环境污染已经逐渐影响到人类的生存和社会的发展。电动自行车的出现不但缓解了道路交通和自然环境的压力，而且降低了能源的消耗。但电动自行车还存在着一系列亟待解决的问题，例如续航里程短、电池寿命短、废弃的蓄电池对水和土壤污染严重等。利用涡卷弹簧受载收紧时将机械能转变为变形能储存，卸载时又能够将储存的变形能转变为机械能或动能的特点，将其与发电机结合直接发电取代蓄电池充放电来给电动自行车提供动力，这可以极大程度地摆脱废弃蓄电池对环境的危害。相较于其他储能方式，弹簧储能具有无污染、结构简单、成本低廉、转换效率高并且可控性好等优点。目前，将储能弹簧应用于电动自行车的发电机上的技术以及针对涡卷弹簧受力问题研究的文献比较少。文献［1］利用ANSYS分析了涡卷弹簧的最大等效应力，并进行了疲劳分析；文献［2］利用圆渐开线作为弹簧的型线，利用有限元法分析其刚度的变化；文献［3］利用ANSYS Workbench对微电机电刷用涡卷弹簧进行了优化设计；文献［4］对张力补偿装置中的涡卷弹簧进行了失效分析，并利用ABAQUS对其进行了模拟仿真；文献［5］利用workbench模拟出涡卷弹簧旋转一定角度时的应力分布，拟合出旋转165°时旋转角度与末端受力的关系曲线；文献［6］将涡卷弹簧应用到双足机器人的腿部来提供前进动力，同时实现了腿部关节单向旋转；文献［7］在机动车辆动能回收系统中提出了在制动过程中使用弹簧收集能量的方法。目前研究涡卷弹簧的文献大多集中在了对二维模型进行仿真分析，并且涡卷弹簧的旋转角度大多局限在1圈之内；分析过程中设置的接触对很多，稍有遗漏就很容易出现计算不收敛的情况；对涡卷弹簧受到转矩的驱动完全收紧时，各层弹簧表面上应力分布情况以及涡卷弹簧整体应力变化规律的研究较少。

基于弹簧能量存储和转换特点，设计了一种应用于电动自行车上的涡卷弹簧储能式发电系统，对该发电系统上的涡卷弹簧进行参数设计与三维建模，并对涡卷弹簧的收紧过程进行有限元分析，得到其在收紧过程中的簧片位移与应力分布规律以及在完全收紧时各层弹簧上最大应力的变化规律，确定了涡卷弹簧储能时的危险截面，对提高涡卷弹簧储能式发电系统的可靠性具有重要的理论与实际意义。

2 弹簧储能式发电系统方案设计

弹簧储能式发电系统的工作原理图如图1所示。工作时，在启动电源1的作用下加能电机2工作，带动加能锤3旋转，反复击打加能杠杆4，与加能杠杆另一端相连的弹簧随之发生变形，棘轮6抑制弹簧反旋，从而完成能量的储存。弹簧释放能量时，在三级增速齿轮的传递下，发电机产生电能。这其中一部分电能用来驱动电动机从而可以取代外部启动电源的位置，另一部分电能用来给电动自行车供电。

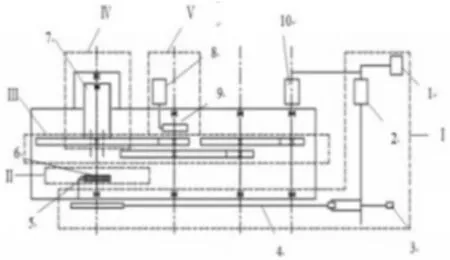
图1 系统工作原理图Fig.1 Working Principle Diagram of the System

在本方案中，储能机构是该发电系统的核心部分。其中储能弹簧是储能机构的核心元件，其设计质量直接影响到了整个系统的可靠性与安全性。由于涡卷弹簧具有变形角大、储能密度高、在较小体积内可以储存较多的能量的特点，因此选择它作为弹簧储能式发电系统的储能元件。

3 涡卷弹簧参数设计与建模

以经过三级齿轮增速驱动输出功率为300W，输出电压24V，额定转速750r/min的发电机为目标，对涡卷弹簧进行设计。涡卷弹簧厚度h为1mm，宽度b为200mm。材料选用60Si2CrVA，其弹性模量E为206GPa，抗拉强度σb为1862 MPa。涡卷弹簧最大理论转矩［8］Tmax为：

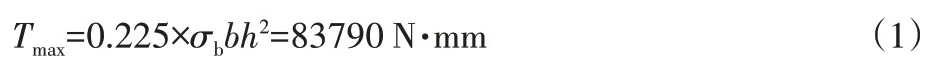
涡卷弹簧最大输出转矩Tsmax为：

式中：K—修正系数，与弹簧外端的固定方式有关。采用衬片固定，取K=0.93，得：Tsmax=77924.7 N·mm

涡卷弹簧最小输出转矩Tsmin为：

取系数为0.6，得：Tsmin=46754.82 N·mm

涡卷弹簧轴半径r为：

式中：m—弹簧的强度系数。取m=13，得弹簧轴半径r和直径d分别为：r=13 mm，d=26 mm。

已知弹簧盒内半径R和弹簧轴半径r的比值为3时，弹簧的有用能量最大［9］，得弹簧盒内半径为：R=39 mm。

弹簧放入弹簧盒中放松时的圈数nmax为：

弹簧的空圈数n0取1～3.5圈，为了便于计算取n0=1.14。弹簧的工作圈数ng为：

涡卷弹簧的工作长度Lg为：

涡卷弹簧自由状态时圈数nz为：

经计算，涡卷弹簧的设计参数如表1所示。

表1 涡卷弹簧设计参数Tab.1 Design Parameters of the Scroll Spring

涡卷弹簧内端面通过螺钉固定在轴上，外端通过螺栓固定在套筒上。利用SolidWorks建立装配体模型。基于结构和载荷的对称性，只建立1/2模型进行分析，并对阶梯轴进行了简化。这样不仅可以大大缩短计算时间，而且接触面上节点减少一半，接触分析更容易收敛。其1/2模型如图2所示。

图2 涡卷弹簧的1/2模型Fig.2 1/2 Model of the Scroll Spring

4 有限元分析

涡卷弹簧旋转收紧的过程中，弹簧自身发生大变形，接触关系复杂而且不易确定，属于复杂的非线性问题。在进行有限元分析时，如果单元的插值函数以节点位移为基本未知量，在采用有限单元法求解时，最终会归结为求解下列形式的平衡方程［10］：

式中：{}u—节点位移矢量；{}R—节点载荷矢量；[]K—刚度矩阵。

对于非线性问题，[]K与节点位移有关。ABAQUS/Explicit适于求解复杂的非线性动力学问题和准静态问题，对接触条件变化的高度非线性问题非常有效。针对涡卷弹簧旋转收紧过程中复杂的接触问题，可以直接建立通用接触面，操作简单且结果容易收敛。将1/2模型导入ABAQUS/Explicit中，对涡卷弹簧的旋转收紧过程进行显式动态分析。

4.1 定义材料属性

在ABAQUS中分别对涡卷弹簧和轴赋予60Si2CrVA和45钢材料属性，其性能参数如表2所示。定义轴截面类型为solid，涡卷弹簧截面类型为shell。这是因为弹簧的厚度相对于长度而言比较小，并且利用壳单元计算可以节省计算资源。

表2 性能参数Tab.2 Performance Parameters

4.2 划分网格

采用扫略法对涡卷弹簧划分网格，网格形状为Hex-dominated，单元类型为S4R。设置轴为六面体网格，单元类型为C3D8I。划分完网格之后，涡卷弹簧单元个数为49511个，轴的单元个数为9207个，共有节点总数为60865个。

4.3 设置时间步

在Step模块中，时间步类型选择显式动态，同时打开Nlgeom，因为旋转时涡卷弹簧模型存在较大的转动。第一个分析步Initial，自动生成涡卷弹簧的外界条件；第二个分析步，对参考点施加一个微小转矩，使各接触关系平稳地建立起来；第三个分析步，对参考点施加真实转矩，涡卷弹簧内端开始随轴旋转。

4.4 设置约束和接触

设置约束和接触时先建立三个表面：轴的外表面、轴的外端面、涡卷弹簧与轴接触部分的内表面。涡卷弹簧与轴之间的接触类型为绑定约束。建立一个参考点，将参考点与轴建立运动耦合关系，限制轴端面X、Y、Z三个方向的平动和转动自由度。

采用通用接触算法、Surface to surface接触方法和库伦摩擦计算公式，设置摩擦系数为0.05。这是涡卷弹簧自接触时有润滑油的状态下的自摩擦系数。接触压力和间隙采用默认的“硬接触”。

4.5 设置边界条件和施加载荷

分别对弹簧外端面、参考点以及弹簧与轴的对称面建立集合set1、set2、set3。限制set1沿X、Y、Z方向的平动和转动自由度，set2沿X、Y、Z方向的平动自由度和Y、Z方向的转动自由度，set3沿X方向的平动自由度以及Y、Z方向的转动自由度。设置好的边界条件如图3所示。对set2施加转矩时，在第一个分析步中，分别对初始转矩为1 N·mm、3 N·mm……45 N·mm，初始时长为0.01s、0.02s……0.06s的情况进行组合并进行有限元计算。通过对比多次有限元分析的结果，最终确定出在第一个分析步中初始转矩为1 N·mm、初始时长为0.01s时，各接触关系的建立更平稳，整个分析过程更高效。在第二个分析步中，由于所建立的是1/2模型，施加转矩大小为41895 N·mm。

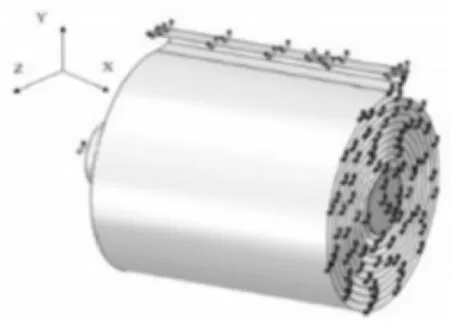
图3 施加边界条件与载荷Fig.3 Apply Boundary Conditions and Loads

5 结果分析与讨论

5.1 旋转过程簧片位移分析

利用ABAQUS/Explicit对涡卷弹簧的旋转收紧过程进行分析，得到其绕X轴旋转过程中簧片的位置分布情况。图4是在YZ平面内观察到的簧片位移图。

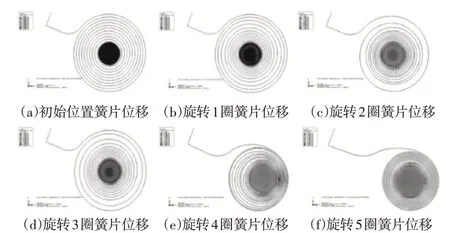
图4 簧片位移图Fig.4 Reed Displacement Diagrams

通过分析图4可以得出，涡卷弹簧在转矩驱动下收紧过程中，首先从涡卷弹簧与轴表面的连接处开始旋转，且前3圈旋转时相邻簧片间隙均匀。旋转到第4圈时，远离固定端的一侧簧片间隙率先发生变化，并且远离固定端一侧的簧片间隙减少量要大于靠近固定端侧的簧片间隙减少量。其第5圈旋转结束时，各簧片间隙又趋于均匀。整个收紧过程中簧片间隙呈现出先均匀减小，然后远离固定端的一侧急剧减小，最终又均匀减小的变化趋势。

取涡卷弹簧最内端边上的节点13286，建立时间t与节点Y方向位移Uy之间的曲线图，如图5所示。其达到Y方向位移峰值的次数即为弹簧内端转过的圈数。观察曲线图可以发现，在前0.01s节点位移没有发生变化，这段时间所施加的转矩只是为了让接触关系平稳地建立起来，涡卷弹簧并未旋转。旋转第1-5圈所用时间分别为0.033s、0.008s、0.008s、0.006s、0.005s。每圈的时长不同，且逐渐减小。这是因为利用ABAQUS求解非线性问题时，如果两个连续的增量步在5次迭代之内就获得了收敛解，下一个增量步自动增加，因此每圈所用时长逐渐减小。

图5 节点t—Uy曲线图（N=13286）Fig.5 Node t—Uy graph(N=13286)

从图5中可以看出，每圈旋转结束时，波谷处的Y方向位移值不同，波峰波谷差值逐渐减小，这意味着节点Y方向整体位移减小。这是因为在开始旋转时，节点13286并未紧贴在轴表面，随着旋转圈数的增加，外层弹簧逐渐向轴上收紧，各层弹簧对最内端弹簧的挤压力增加。在挤压力的作用下，最内端边上的节点13286逐渐向轴表面靠近，节点Y方向的整体位移更接近26 mm。节点先后5次到达峰值，第5次没有完全回到起始点，而是停留在了16 mm（4.75圈左右）的位置。这是因为在对涡卷弹簧进行设计时，并未考虑相邻簧片之间摩擦力的影响，算得驱动涡卷弹簧1/2模型旋转5圈需要的转矩为41895 N·mm。在模拟时，考虑了润滑状态下相邻簧片之间摩擦力，涡卷弹簧最终并未旋转到5圈。

5.2 应力分布分析

施加转矩后，获得涡卷弹簧绕X轴旋转不同圈数时的Mises等效应力分布情况，其等轴测视图，如图6所示。

图6 应力分布云图Fig.6 Stress Distribution Nephograms

分析图6可得，涡卷弹簧上的应力首先在弹簧内端与轴绑定的位置产生。并且随着涡卷弹簧的旋转圈数增加，应力从最内端开始产生并逐渐向外端延伸，应力值由内向外逐渐减少。涡卷弹簧的固定端与活动部分的拐角处应力较大，在弹簧反复收紧和释放的过程中可能发生断裂，属于危险截面。实际产品中应采用较为圆滑的方式连接固定端与活动部分。

分析旋转不同圈数时的应力分布云图可以发现，当弹簧旋转第3圈时，在靠近弹簧内端与轴绑定的位置开始出现应力集中现象。当涡卷弹簧旋转到第5圈时，在靠近与轴绑定的位置处应力值最大，应力集中现象最为明显。这是因为弹簧自身厚度为1 mm，弹簧内端与轴绑定位置相比于圆滑的轴表面凸起了1 mm。在弹簧收紧时，外面的多层弹簧紧压在绑定位置的凸起处上，出现了应力集中现象。由于有限元模型中网格单元的棱角比实际产品的要尖锐许多，所以并不一定导致产品失效。在实际应用中，将涡卷弹簧固定在轴上之前，要将弹簧内端加工成渐增型并且打磨光滑，使其厚度逐渐过渡到1 mm，从而减小应力集中的发生。

5.3 应力集中现象分析

分析应力分布云图中得出，当旋转到第5圈时，在涡卷弹簧内端与轴绑定位置有应力集中现象。绘制出此时该区域上应力集中现象最明显的各层弹簧上的节点Mises等效应力变化曲线，如图7所示。

图7 节点应力变化曲线图Fig.7 Graphs of node stress change

提取出旋转5圈后，各层弹簧上应力最大处节点Mises等效应力值，如表3所示。

表3 旋转至第5圈时，各层最大应力Tab.3 Maximum Stress at Each Layer when Rotated to the 5th Lap

综合分析图7，并结合表3中的数据发现，随着弹簧旋转圈数的增加，节点上的应力值逐渐增大；旋转到第3圈时，靠近涡卷弹簧内端与轴绑定区域开始出现应力集中现象；旋转到第5圈时，在靠近涡卷弹簧内端与轴绑定区域的应力集中现象最为明显。此时最大应力发生在该区域第4层弹簧处，大小为2314 MPa。在完全收紧时，应力集中区域处各层弹簧上的最大应力呈现出沿径向先增大后减小的变化趋势。

6 结论

设计了一种应用于电动自行车上的涡卷弹簧储能式发电系统，对涡卷弹簧进行了参数设计与三维建模，并对涡卷弹簧在收紧过程中的簧片位移、应力分布情况进行了动态分析，得到如下结论：

（1）涡卷弹簧在旋转收紧的过程中，首先从弹簧与轴表面的连接处开始旋转。整个收紧过程中簧片间隙呈现出先均匀减小，然后远离固定端的一侧急剧减小，最终又均匀减小的变化趋势。

（2）涡卷弹簧的固定端与活动部分的拐角处应力较大，在弹簧反复收紧和释放的过程中容易发生断裂，属于危险截面。实际产品中应该采用圆滑过渡的方式连接固定端与活动部分。

（3）旋转收紧过程中，涡卷弹簧上的应力首先在弹簧内端与轴绑定的位置产生。随着涡卷弹簧的旋转圈数增加，应力从最内端开始产生并逐渐向外端延伸，应力值由内端向外端逐渐减少。在靠近弹簧内端与轴绑定的位置存在应力集中现象。原因是在弹簧内端与轴绑定位置，由于自身厚度的影响，弹簧相比于圆滑的轴表面凸起了1 mm。在实际应用中，将涡卷弹簧固定在轴上之前，要将弹簧内端加工成渐增型并且打磨光滑，使其厚度逐渐过渡，从而减小应力集中的发生。

（4）涡卷弹簧在完全收紧时，应力集中区域处各层弹簧上的最大应力呈现出沿径向先增大后减小的变化趋势。