基于动力学分析的差速驱动AGV原地转向稳定性研究

张 瑞，卢林芳，王婷婷

（郑州大学机械工程学院，河南 郑州450001）

1 引言

自动导引运车是一种以电池为动力，装有电磁导引设备或光学导引设备，能够自动沿着预定轨道行驶的自动化车辆［1］，应用于仓储物流中，极大地提高自动化水平、降低人工成本，但其安全性与稳定性仍需做深入分析与研究［2］。某型前轮差速驱动式偏心货叉AGV可实现在仓储物流运输中零半径原地转向，但在转向过程中其稳定性较差，出现AGV侧滑，驱动轮滑转/滑移等现象。目前，国内外有许多针对AGV差速转向的研究。其中，文献［3］通过静力学分析，研究差速转向的可行性，并根据仿真，验证了差速转向的可行性。文献［4］对AGV小车静力学模型进行分析，验证了一个驱动轮静止，另一个驱动轮运动这种转向方式的可行性。文献［5］分析了轮式车辆速差转向过程中轮胎工作状态，并参考履带车辆转向理论，得出速差转向轮式车辆的转向阻力系数模型。但针对这种偏心式AGV原地转向稳定性的理论研究较为缺乏。

针对差速驱动式AGV原地偏心转向模型，进行动力学分析，推导AGV转向稳定性的理论公式，获得车体结构参数与运动参数对AGV转向稳定性影响，并通过仿真实验，验证了理论推导的正确性。最后，依据理论推导以及仿真，对相关参数进行优化，改善了AGV转向的稳定性。

2 AGV模型及参数

货叉式前轮差速驱动偏心AGV如图1所示，AGV前侧为货叉，后侧布置电池、电机、配重块等，车身为框架结构，两前轮为差速驱动轮可实现原地零半径转向，后轮为万向轮起支撑作用，转向时能够满足阿克曼几何学原理［6］。该AGV用于仓储物流，水平路面运行，速度不超过1.5 m/s，属于平面低速运动［7］。AGV通过二维码引导直线行驶，到指定位置后前轴左右两轮执行反方向同转速运动，带动AGV绕旋转中心O（如图2所示），实现匀加速-匀速-匀减速运动使车体转向90°。

图1 AGV实车模型Fig.1 AGV Model

图2 AGV简化模型Fig.2 Structure Sketch of AGV

AGV总质量为m，两驱动轮的轮距为B，前后轴距为L，车体质心位于C点，偏心距为e，质心高度H，驱动轮与地面之间的静摩擦系数根据AGV运行路面及车轮材料确定为μs=0.6，滚动摩阻系数fR。

3 AGV转向稳定性分析

针对AGV原地加速度转向过程分析，AGV受力如图3所示，两驱动轮y方向上受地面对其作用力Fy1、Fy2，x方向上受静摩擦力Fxs1、Fxs2；万向轮上受滚动阻力FR3和FR4，分解得FxR3、FxR4、FyR3和FyR4；惯性力在x、y方向的分解，得

图3 AGV受力分析Fig.3 Force Analysis of AGV

到F′x和F′y。采用动静法［8］，列出平衡方程：

两侧驱动轮垂向载荷相等，则式（1）为：

代入公式（2）-（4）中：

3.1 AGV出现侧滑导致转向不稳定

根据公式（1），在x方向上，当驱动轮的最大静摩擦力合力小于AGV所受其它合力时，AGV将出现侧向的滑动，为避免此发生，则：

将AGV相关尺寸、系数代入（7）中，即：

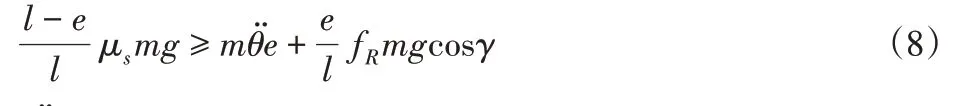
式中：—AGV在转向过程中的角加速度，γ—万向轮滚动阻力与其x方向上分力的夹角。

3.2 驱动轮出现滑转/滑移导致转向不稳定

AGV加速转弯过程中，当地面给驱动轮提供的力形成的力矩无法达到小车圆周运动的惯性力矩时，驱动轮将出现滑转，为避免该情况的发生：

图2中，惯性力会对车体载荷转移造成影响。Fx′造成左右轮子载荷转移，Fy′造成前后轮载荷转移。分别以右侧轮、后轮与地面接触点为支点，列力矩平衡方程：

式中：N1—轮1、3所受支持力，N1′—轮1、2所受支持力，以左侧驱动轮1为对象，由公式（9）、（10）、（11）得：

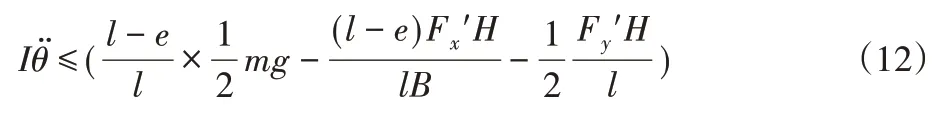
公式（12）为考虑载荷转移后，驱动轮避免出现滑转/滑移的条件，对比公式（9），可以看出，实际情况相对于不考虑载荷转移时驱动轮更易发生滑转/滑移。

3.3 两驱动轮加速度值差异导致转向不稳定

左侧驱动轮的受力分析如图4所示，轮半径为r，质量为m1，车身对轮的作用力为FP，驱动力偶矩Me，地面对驱动轮的支撑力N，以及驱动轮做平面运动的惯性力FQ=m1a和惯性力偶MQC′=IC′α，AGV转向时产生的惯性力F′y在左边驱动轮上的分力Fy1′，Fy1′为公式（5）、（6）中的最后一项驱动轮作纯滚动时：

图4 驱动轮受力Fig.4 Force Analysis of Driving Wheel

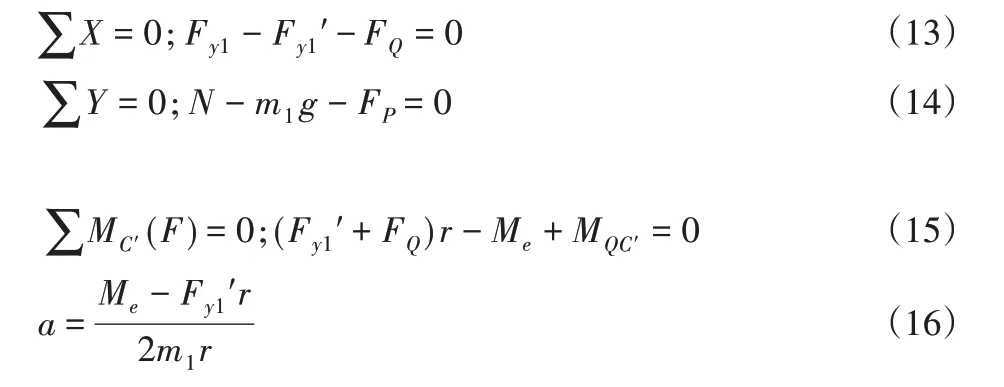
同理，对右侧驱动轮进行分析，可得：

两驱动轮轮心位移速度实时相等才能保证AGV实现零半径的 原 地 转 向，而 公 式（16）与 公 式（17）中，由 于Fy1′≠0导致左右驱动轮的加速度不相等，因此产生AGV转向不稳定。

由公式（8）、（12）、（16）、（17）可知：AGV原地转向的稳定性涉及AGV车体转向角速度、角加速度、质心位置以及车体尺寸因素。为进一步分析各参数对AGV原地转向稳定性的影响，后文通过仿真分别进行分析，而上述推导为后文的仿真研究提供理论依据。

4 AGV原地转向仿真分析

通过上述理论推导，得出影响AGV原地转向稳定性的相关参数。采用ADAMS软件对AGV原地转向进行仿真，分别针对所推导公式中的角速度θ˙、角加速度θ¨、偏心距e以及车体尺寸等参数进行仿真实验，仿真模型，如图5所示［9］。

图5 AGV仿真模型Fig.5 AGV Simulation Model

4.1 速度对AGV转向稳定性的影响

由于车体转向角速度取决于驱动轮角速度，为方便设置，对AGV驱动轮不同转速下驱动轮轮心位移速度进行仿真，得到旋转中心的最大偏移量曲线以及驱动轮角速度为1445 deg/s的轮心位移速度曲线，如图6～图7所示。

图6 最大偏移量曲线Fig.6 Maximum Offset Curve of Rotation Center

图7 驱动轮轮心位移速度曲线Fig.7 Driving Wheel Displacement Velocity Curve

由仿真结果可知，AGV低速时，旋转中心的最大偏移量（转向过程中，理论上旋转中心点位置与实际上该点的最大差值）不到1.5 mm。当速度较大时，如图7所示，两驱动轮加速度的差值较大，随着速度的增大，这种差值增大，旋转中心的偏移量变大，验证了公式（16）、（17），随着速度的增大，两驱动轮的加速度值差异增大，导致旋转中心在水平面上的偏移量增大。

4.2 加速度对AGV转向稳定性的影响

针对不同加速度进行仿真，结果如图8，以及在0.1 s的加速时间下驱动轮轮心位移速度曲线，如图9所示。

图8 最大偏移量曲线Fig.8 Maximum Offset Curve of Rotation Center

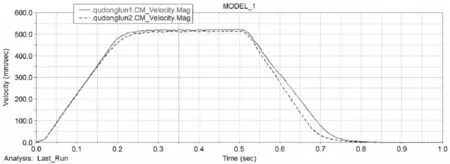
图9 驱动轮轮心位移速度Fig.9 Driving Wheel Displacement Velocity Curve

从图8看，加速度对两驱动轮的速度差异影响并不大，符合之前动力学平衡方程：加速度只对AGV的x方向上的受力起影响。在加速度时间小于0.3 s，旋转中心最大偏移量的变化明显要大于加速时间大于0.3 s，符合公式（8）所分析：加速度达到一定时，x方向上的惯性力大于车轮的最大静摩擦力，AGV会出现滑动；图9中，加速时间为0.1 s，AGV在设置的停止转动时继续运动，驱动轮出现了明显的运动迟滞，随着加速度的增大，这种现象更加明显。

4.3 质心位置对AGV转向稳定性的影响

质心位置包括水平方向的位置，即偏心距e和质心高度H。对不同偏心距的AGV转向进行仿真实验，得到相应的仿真结果，以及偏心距为20 cm时驱动轮轮心位移速度曲线。

从图10看，旋转中心的偏移量随偏心距的增大而增大。如图11，偏心距较大时，两驱动轮的速度差异相当明显，对应的旋转中心的偏移量也非常大。偏心距在公式（8）、（9）、（11）以及公式（12）中均有涉及，偏心距对稳定性很重要，它会使转向过程中出现驱动轮侧滑，滑转/滑移以及驱动轮加速度不一致。

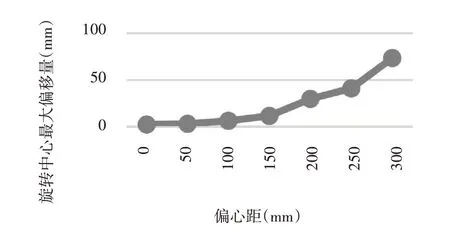
图10 最大偏移量曲线Fig.10 Maximum Offset Curve of Rotation Center

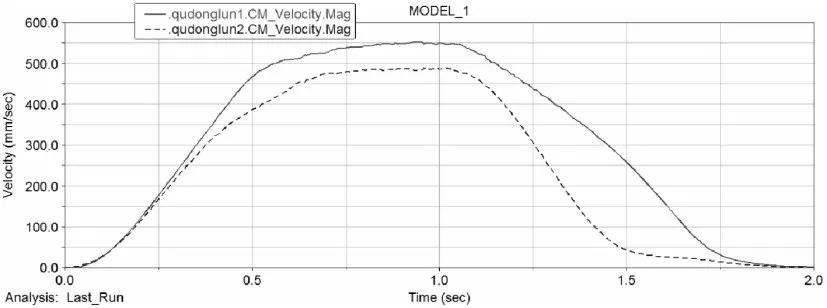
图11 驱动轮轮心位移速度曲线Fig.11 Driving Wheel Displacement Velocity Curve

固定偏心距，对不同的质心高度进行仿真，其对稳定性的影响，如图12所示。

图12 各质心高度下旋转中心最大偏移量情况Fig.12 Maximum Offset Curve of Rotation Center in Different Centroid Height

由图12可知：质心高度对AGV转向稳定性影响很小，质心高度从10 cm到55 cm，其旋转中心最大偏移量的变化范围仅在6～12 mm之间。质心高度H对转向时驱动轮出现滑转/滑移现象有较小影响。

4.4 车体尺寸对AGV转向稳定性的影响

车体尺寸包括车体长度、宽度，分别对车体长度、宽度进行仿真实验，得到以下仿真结果。

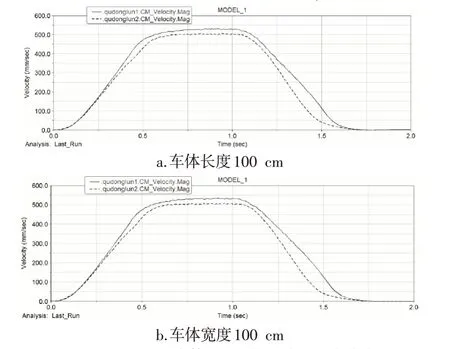
图14 不同长、宽车体驱动轮轮心位移速度曲线Fig.14 Displacement Velocity Curve of Driving Wheel in Different Length and Width of Vehicle Body

从图13、14看，车体长度、宽度对AGV转向影响较小，且长度与宽度对AGV转向的影响在量上近乎一致，与理论分析一致。从驱动轮速度曲线来看，车体长宽不同时，两驱动轮达最大速度时的速度差异并不大，而车体长宽偏大，运动迟滞现象更明显，验证了公式（9）中车体长宽的增大引起AGV转向过程中惯性力矩过大，造成驱动轮出现滑转/滑移。

图13 不同车体尺寸下旋转中心偏移情况Fig.13 Maximum Offset Curve of Rotation Center inDifferent Size of Vehicle Body

5 AGV结构优化

通过上述分析与仿真可知，AGV转向速度、加速度、偏心距以及车体尺寸对其转向稳定性影响比较大。对这些参数进行优化，以提高AGV原地转向稳定性。

偏心距过大导致AGV转向出现滑转、两驱动轮加速度值差异过大以及驱动轮出现滑转/滑移，而偏心距过小又会导致AGV在减速过程中出现前倾。对前轮与地面接触为支点，列力矩平衡方程：

式中：N2′—地面对后轮的法向载荷，当N2′为0时，AGV有前倾的危险，a′—AGV直线行驶时的最大减速度，发生在AGV紧急停车时，需要在100 mm内从速度1 m/s减到0，可得a′—5m/s2。H取原设计的30cm，N2′为0时，得e=15.3cm。

对车体尺寸进行基于稳定性的轻量化设计，建立车体结构优化模型。

min：AGV车体框架体积

设计变量：框架边长以及型材截面边长

约束：材料许用强度

优化后的结果，如表1所示。

表1 优化前后各参数值Tab.1 Parameter Values before and after Optimization

AGV结构优化后，再次仿真，优化前后仿真结果如图15、16所示，相同速度、加速度下，优化前两驱动线速度一致性较差，优化后两驱动轮线速度曲线几乎保持一致；优化前，驱动轮加速和减速结束时都出现较为明显的滑转/滑移，而优化后，车体在驱动轮停止加速、减速时车体停止运动，即没有滑转/滑移；优化后的AGV旋转中心偏移量大幅度减小，从最大偏移量接近12.5 mm降至仅4.6 mm。综合分析，AGV原地转向的稳定性在结构以及尺寸优化后得到很大的改善。

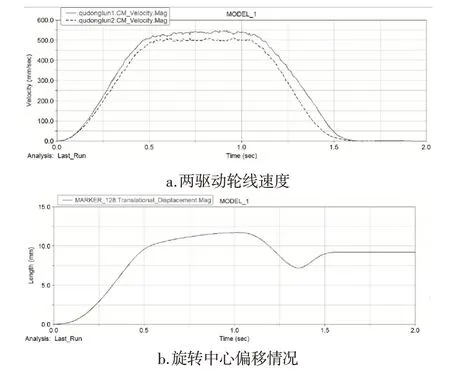
图15 结构以及尺寸优化前的稳定性情况Fig.15 Stability of Vehicle Structure and Size before Optimization

图16 结构以及尺寸优化后的稳定性情况Fig.16 Stability of Vehicle Structure and Size after Optimization

将优化结构参数代入公式（8）、（9），为了使转向过程时间最短，求得AGV驱动轮线加速度amax=2.34m/s2。

AGV转向速度的增大造成转向过程中两驱动轮加速度差异增大，而为了快速完成转向，AGV的速度不应过低。通过不同速度下的仿真实验，寻求AGV能够稳定转向，又能以较快速度完成转向的最优速度值。仿真结果如图17所示，由于该AGV采用二维码导航的方式，根据相机识别的范围（12 cm×15 cm），以及二维码的边长（2 cm×2 cm），可以算出允许最大偏差距离为4.586 cm，则驱动轮角速度为1341 deg/s既符合要求，又保证最快速度转向。

图17 各速度下旋转中心最大偏移Fig.17 Maximum Offset Curve of Rotation Center in Different Speed

6 结论

（1）对AGV偏心原地转向过程进行动力学分析，获得相应的理论公式，得出AGV结构参数与运动参数同原地转向的稳定性的定性关系；

（2）采用ADAMS对AGV原地转向过程进行仿真，分别针对速度、加速度、偏心距、车体尺寸等参数进行仿真实验，通过各参数对AGV转向稳定性的影响规律分析，验证了理论推导的可靠性；

（3）最后，对AGV结构优化，获得新的AGV结构参数与运动参数，结合仿真分析，AGV原地转向的稳定性得到了改善。