单参数平底刀底刃加工叶片进排气边刀位优化算法
2021-09-23李珊珊甘植旺陈志同
李珊珊,甘植旺,陈志同
(1.北京航空航天大学机械工程及自动化学院,北京100191;2.北京航空航天大学先进航空发动机协同创新中心,北京100191;3.中国电子科技集团公司信息科学研究院,北京100086)
1 引言
刀位优化算法是数控加工的必要构成技术,是提升零件加工效率与质量的有效途径[1]-[6]。叶片进排气边的加工存在加工效率低,易产生颤振的问题[6]-[11]。进排气边与叶身的面积之比小于,但加工时间之比大于提高进排气边区域加工效率,是实现航空发动机叶片高效制造的必要技术途径。进排气边为凸曲面,因此从几何匹配角度考虑,该类曲面可以使用凸型母线刀具、凹型母线刀具以及平型母线刀具进行加工。与凸型母线刀具相比,凹型母线刀具及平型母线刀具能够更加高效地完成叶片进排气边的加工[7],[9]-[11]。
黄魏等使用圆弧半径为1mm的凹型母线刀具,对圆角半径为0.35mm~0.9mm的进排气边进行加工,相比于圆角立铣刀其加工效率提高了5倍[9]。贺英等使用半径为8mm及0.3mm的凹型母线刀具,分别对圆角半径在6.2mm~6.9mm及0.16mm~0.22mm的进排气边进行加工,相比于圆角立铣刀其加工效率至少提高了4倍[10]。但使用凹型母线刀具加工进排气边存在接刀问题,进排气边尺寸小,接刀痕对其质量评定的影响十分显著。该问题涉及精确对刀,铣削振动,铣削力控制等多个复杂问题。
平型母线刀具加工进排气边包括直刃刀侧铣及平底刀端铣两种实现方式。由于刀柄及辅助结构的存在,使用直刃侧铣会出现干涉。叶身使用平底刀加工,因此使用平底刀底刃加工进排气边,不仅能够提升加工效率,而且能够避免接刀问题。张春等定义了平底刀具加工进排气边的刀具位姿确定方法,定性地分析了刀具定位点及偏航角对行宽的影响,以行宽最优为目标进行刀位求解[11]。但现有的平底刀底刃加工进排气边算法所生成的刀轨的光顺性不能满足加工要求,颤振严重,不能够应用于进排气边的加工。
本文将构建能够满足刀轨光顺性要求的平底刀具底刃加工进排气边的刀位优化算法。现有刀位优化算法具有两个优化参数:偏航角及刀具定位点参数。本文将平底刀底刃加工进排气边的刀位优化过程转化为平面上直线与圆的问题,进而论证了偏航角的冗余性,同时将刀位优化过程转化为单参数优化过程。在此基础上,分析了刀具定位点参数一致性的利弊,最终确定了统一刀具定位点的刀位优化策略,最大程度上减少了因刀具位姿参数变动带来的刀轨波动。此外,相比于同类刀位优化算法,该方法能够获得更大的行宽。
2 基础知识
2.1 坐标系与姿态角
回转刀具的数控加工过程,存在四个坐标系即:绝对坐标系(Absolute Coordinate System,ACS),刀具坐标系(Tool Coordinate System,TCS),局部工件坐标系(Local Workpiece Coordinate System,LWCS),和局部刀具坐标系(Local Tool Coordinate System,LTCS),如图1所示。若无特别说明,本文所提到的坐标系均为右手坐标系。

图1 坐标系与姿态角Fig.1 Coordinate Systems and Orientation Angles
ACS是一个确定的坐标系。该坐标系由原点O和轴构成。所有的运算与表达最终都要转化到ACS上。TCS是与刀具固连的右手坐标系。该坐标系为获得刀具上点的相对位置关系提供了方便,因为在该坐标系下可以不考虑刀具的运动和位置。该坐标系以刀具中心OT为原点,以刀轴为zT轴,以通过刀轴的某一平面为其xT zT平面。
LWCS与LTCS是实现刀具定位的坐标系。若P为当前驱动点为P点单位法矢为P点进给方向,ρ为抬刀量,r为刀具圆角半径,oT为刀具圆角中心,OT为刀心点,Q为刀具上选定点,为Q点 单 位 法 矢为Q点 沿 刀 具 母 线 单 位 切 矢。定 义为其(xt,yt,zt)坐标轴的单位矢量。定义LWCS以为原点,且代表其(x,y,z)坐标轴单位矢量。对于刀具圆角非零的刀具,LTCS原点为刀具圆角圆心。且当以调整姿态角方式优化刀具位姿时,Q点选定为即刀具上法矢平行于刀轴矢量的点。
常用的刀具初定位方法为:匹配LTCS与LWCS。LTCS与LWCS匹配意味着Q与P相切触,且同向。本文的刀位求解过程基于该刀具初定位方法。由该方法确定的刀心点径矢t→C及刀轴矢量t→A分别为:

刀具初定位后,其刀具位姿通过调整其绕LTCS的各个坐标轴的转动来实现。如图1所示,刀具绕LTCS的x轴转动的角定义为滚摆角,记为ψ;绕LTCS的y轴转动的角为俯仰角,记为θ;绕LTCS的z轴转动的角为偏航角,记为φ。文献[12]已证明,若(θ,φ,ψ)为上述转动后获得的刀具位姿,则该刀具位姿可由刀具依次绕LWCS的x轴转动ψ,y轴转动θ,z轴转动φ获得。本文中借助绕LTCS的转动描述刀具位姿。
2.2 多参数平底刀底刃刀位优化算法
定义刀具定位点与刀心点的距离为刀具定位点参数,记为ℎ。选择刀具底刃上的点作为刀具定位点,在刀具与工件切触后,为保证位姿优化过程中无干涉,只有偏航角φ能够继续优化。本文中的多参数平底刀底刃刀位优化算法是指张春等定义的以平底刀具加工进排气边的刀具位姿确定方法,该刀位优化过程以φ及ℎ作为刀位优化变量,以最优行宽作为优化目标[11]。本文以{a,b}的形式定义ℎ=a,φ=b的刀具位姿。
分析{ℎ,φ}参数下刀具位姿的计算过程。选定刀具上Q点作为刀具定位点,且LTCS、LWCS与2.1中定义一致。匹配LTCS与LWCS初定位刀具,如图2所示,刀具在初始姿态时同向,ACS下的刀具初始位姿为:

图2 平底刀底刃加工进排气边Fig.2 Flat-end Cutter Bottom Machining the Leading Exhaust Blade Edge
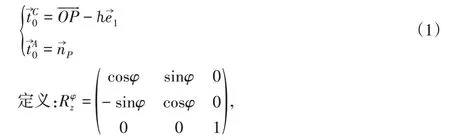
式中:—绕坐标系z轴旋转φ的旋转矩阵。偏航角φ对于刀具位姿的调整是刀具沿LWCS的原点绕其z轴旋转φ,旋转后与x轴负半轴夹角为φ。结合(1)式,以{ℎ,φ}为参数的刀具位姿为:
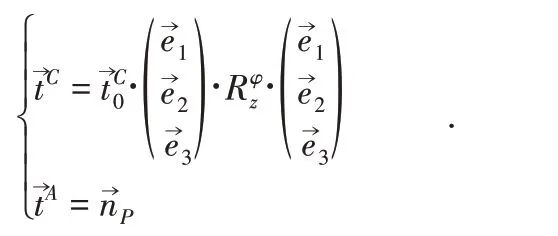
文献[11]给出了刀具定位点参数为ℎ,偏航角为0的行宽W(ℎ,0)的估算公式
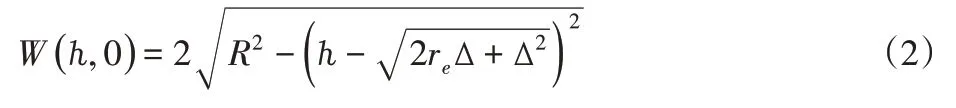
式中:re—加工位置点沿叶宽方向的曲率半径,Δ—公差
3 单参数平底刀底刃加工进排气边方法
3.1 刀具定位点参数与偏航角对行宽影响的等效性
在局部区域内,进排气边沿叶长方向平坦,且沿叶宽方向具有较为一致的曲率半径。进排气边的局部几何属性类似于圆柱面或锥面,以圆柱面或锥面近似进排气边,定性地分析刀具定位点参数与偏航角对行宽影响的等效性。图3为平底刀底刃加工进排气边刀具位姿由{h,0}调整至{h,φ}及{hcosφ,0}的过程,及其简化模型在z视角下的视图。图3(a)描述了位姿调整过程,其中P为驱动点,沿叶宽方向红色曲线为驱动线,蓝色刀具的刀位优化参数为{h,φ},粉色刀具的刀位优化参数为{hcosφ,0}。坐标系P-xyz为LWCS,其构成元素为:P点为其原点,P点法矢为其z轴,P点沿驱动线切矢为其x轴。记Re为P点沿叶宽方向的曲率半径,进排气边在P点的几何属性使用半径为Re的圆柱面及锥面近似。图3(b)为简化模型在LWCS的z轴视角下的示意图,即为在P点切平面上刀具底面圆调整示意图。在图3(b)中建立坐标系P-x′y′,且其以P为原点,以-y方向为x′方向,以x方向为y′方向。OT1、OT2、OT3分别为刀具在{h,0}、{h,φ}及{hcosφ,0}参数下的的刀心点。

图3 位姿调整过程及其在z视角下简化视图Fig.3 Tool Orientation Adjustment Process and its Z-direction View
因在偏航角优化过程中刀轴矢量不变,故刀心位置可作为区分刀具位姿的指标。将进排气边简化为圆柱面或者锥面后,刀位优化过程变为圆相对于平面内直线的位置变化过程;这是因为平底刀底刃上点的法矢与刀轴矢量平行,刀具初定位后,刀具底刃位于驱动点切平面内。在优化偏航角时,是将刀具绕驱动点法矢旋转,刀具底面在优化过程中始终处于驱动点切平面内。对于柱面锥面而言,其切平面内直线是与刀具吻合程度最好的直线,因为和刀具底面处于同一个平面。该直线位于刀具底面圆内部分与行宽关联。所以刀位优化过程可以视为圆和直线的位置变化关系。在xy平面内分析该问题。
参照图3(b),在P-x′y′坐标系下,计算{ℎ,φ}与{ℎcosφ,0}参数下刀具底面圆与直线的交点距离均为不同参数下刀具底面圆与直线的交点距离相同,该距离与行宽相关,因此两组参数求得的行宽相同。即偏航角对行宽的作用可以转化为刀具定位点参数对行宽的作用。刀具定位点参数与偏航角对行宽的影响具有等效性。
3.2 刀具定位点参数一致性分析
(2)式为偏航角为0的行宽计算公式,由该式可知:在确定加工位置行宽W与ℎ负相关。即由其他约束条件所计算出的最小ℎ,是实现行宽最优的ℎ。同一刀轨行设置统一的ℎ能够最大程度的降低刀轨波动程度。由于各加工位置点rs具有差异,因此对于统一的ℎ,各位置行宽存在差别。进而造成过搭接,即同一位置被多次加工,浪费加工资源。但零件质量要求的优先级高于资源的优化配置。因此设置统一的ℎ是一种可取的刀位优化策略。
3.3 刀具位姿优化求解
结合3.2节及3.3节的分析,平底刀加工进排气边的刀位优化过程,可简化为单参数优化过程,ℎ作为刀具位姿优化参数,且同一刀轨行设定统一的ℎ。本文所考虑的约束为切削线速度约束。定义转速为N,线速度约束为Vr。由切削线速度计算公式可知刀具定位点切削线速度为2πℎN,切削线速度与ℎ成正比。因此根据线速度约束可求解出最小刀具定位点参数:

由(1)式可得出以P作为加工位置在{ℎmin,0}参数下的刀具位姿为:

4 实验
以某航空发动机薄厚可调叶片为验证对象,验证本文所提算法在刀轨光顺上的有效性。该叶片曲面尺寸及曲率分析结果如图4(a)所示,叶片长度约370 mm,榫头宽度范围约55mm~100mm,叶片曲面的曲率变化较小,且大部分区域较为一致,排气边沿叶宽方向半径范围为3.35mm~3.85mm。刀具选定为直径16mm,圆角半径为1mm的平底刀,刀具母线如图4(b)所示。编程公差为0.01mm。

图4 叶片尺寸曲率分析及所使用平底刀母线示意图Fig.4 The Size and Curvature Analysis of the Blade Surface
4.1 刀具定位点参数与偏航角对行宽影响的等效性验证
由3.1节分析可知,{ℎ,φ}对行宽的影响等效于{ℎcosφ,0}。现对表1中的4组参数进行刀轨仿真,以仿真结果验证3.1节的分析结果。表1中的4组参数具有如下对照关系:第1组和第2组为对照组,第3组和第4组为对照组,对照组间ℎ和φ满足:

表1 对照组实验参数Tab.1 The Experimental Parameters of Control Groups

式中:n—实验序号,ℎn—第n组的ℎ参数,φn—第n组的φ参数,n=2,4。刀轨数均为20,刀轨方向沿u向,行宽取定为等参数行宽即(0.9-0.1)20。
图5为对照仿真结果,其中图5(a)为第1组参数和第2组参数的刀轨仿真结果。图5(b)为第3组参数和第4组参数的刀轨仿真结果。图5(a)由三部分组成,从左向右分别为:第1组参数所生成刀轨的仿真结果,第2组参数所生成刀轨的仿真结果,仿真数据中余量与颜色的对应关系。观察图5(a)可知,两组参数所生成刀轨的仿真图像的形状、位置、颜色均相同。因此,由第1组参数和第2组参数所生成的刀轨的仿真结果是一致的,即该对照组参数的加工效果一致。观察图5(b)可知第3组参数和第4组参数所生成的刀轨仿真结果也是一致的。刀轨仿真结果与3.1节分析结果一致,即刀具定位点参数与偏航角对行宽的影响具有等效性。

图5 对照仿真结果Fig.5 The Simulation Results about the Parameters
4.3 刀轨波动对比
本节以各轴加速度为指标,对比本文所提算法与现有算法所生成刀轨的波动性。所选加工参数位置为v=0.5,u∈[0.96,1](该区域被排气边所包含)。如表2所示为原有算法所生成的刀轨的各轴加速度变化幅度与本文算法的对比结果。由表可知多参数算法x,y,z轴加速度变化幅度最大为40 mm/s2,本文加速度变化幅度最大为4.5 mm/s2,其加速度波动幅度降低至多参数算法的12%。多参数算法A,B轴加速度变化幅度最大为500 rad/s2,本文算法A,B轴加速度变化幅度最大为13 rad/s2,降至多参数算法的3%。

表2 原有算法与本文算法加速度对比结果Tab.2 The Contrast Results of the Proposed Method and Multi-Parameter Method
4.4 试切实验
以铝合金作为实验材料对本文所提算法进行试切验证,刀具材料选择高速钢。对于该叶片曲面,(u,v)∈[0.93,1]*[0,1]区域覆盖其排气边,且u方向为叶宽方向。以u参数线作为刀轨驱动线。
切削材料为铝合金,刀具材料为高速钢,切削线速度至少为150 m/min[13]。其他加工参数设置如下:主轴转速设定为4000r/min,进给速度设定为600mm/min,切深0.2mm。将线速度约束带入(3)式,可计算出刀具定位点参数为5.972mm,选定刀具定位点参数为6mm,并由(4)式求解各刀具位姿。刀轨如图6(a)所示,共60行。如图6(b)所示为刀轨仿真结果,由该图可知使用本文算法所生成刀轨无过切,且残留量小于0.012mm,符合编程公差要求。使用该算法在铝件上的加工验证结果,由图可知零件表面光洁且无颤振刀纹,如图7所示。

图6 刀轨与仿真结果Fig.6 Tool Paths and the Simulation Results

图7 叶片试切结果Fig.7 The Machined Blade Surface
5 结论
针对平底刀具底刃加工进排气边刀位优化算法所生成刀轨光顺性不能满足加工要求的问题,本文提出了单参数刀位优化算法,有效提高了刀轨光顺性,且不降低行宽。该方法的构建基于对刀位优化过程的有效简化,具体工作如下:
论证了刀位优化过程中偏航角与刀具定位点对行宽作用的一致性,并分析了设定一致的刀具定位点参数的必要性,进而简化了平底刀底刃加工具有柱面或圆锥面特征的进排气边的刀位优化过程,确定了单参数的优化策略。
在某型号发动机薄厚可调叶片模型上完成了试切验证。加工后的零件表面光洁,表面无颤振刀纹,满足加工要求。与原有算法相比,本文算法所生成刀轨的各轴加速度变化幅度降低至对比算法的12%。
