柔性多关节移动机器人末端残余振动控制研究
2021-09-23李林峻党旭丹
李林峻,党旭丹,刘 洋
(1.河南工程学院工程训练中心,河南 郑州451191;2.河南工程学院机械工程学院,河南 郑州451191;3.河南财经政法大学现代教育技术中心,河南 郑州450000)
1 引言
柔性关节机械臂能够高度仿真人体手臂的性能,并采用位置、抵制和阻抗等多种控制方法,在一定应用领域可替代人类操作。但在实际应用中,机器人末端残余的震动可能未引起多关节机械臂的性能,因此需对其振动进行控制。传统机器人末端残余震动控制方法存在操作困难、功能不全面等问题。文献[1]提出了一种基于状态观测器的鲁棒反步控制方法,通过引入状态观测器来实现控制;文献[2]提出了一种基于干扰观测器的控制方法,设置循环系统,增强控制过程的稳定性;文献[3]提出了一种基于模型控制的控制方法,通过估算机器人末端负载端的转速,来实现抑制振动控制。本文深入研究柔性多关节移动机器人末端残余振动控制,通过构建柔性多关节移动机器人末端动力学模型和运动误差模型,以最小姿态为基础设计柔性多关节移动机器人的运动学参数,应用相关算法对其末端残余振动进行控制。
2 柔性多关节移动机器人末端动力学模型
在设计柔性多关节移动机器人末端动力学模型时可以将柔性多关节移动机器人的机械臂杆假设为刚性杆,而只需要考虑柔性关节对移动机器人末端残余振动的影响[4-5]。
将关节柔性模型简化为一种存在于电机转子和下一连杆之间的线性弹簧,忽略机械臂杆和关节之间的摩擦,可列出具体的数学模型公式1如下:

式中:Qi、&i—电机端与连杆端的移动位移;Xi、Mi—电机端与连杆端有效转动惯量;Miz—电机端的转动力度大小;Ti—与柔性关节连接的臂杆所承受的被动力度大小;K—刚度系数。将以上各数据代入到公式(2)中即可得到柔性关机所受到的弹性势能大小,该数据为建立柔性多关节移动机器人末端动力学模型的主要数据[6-7]。
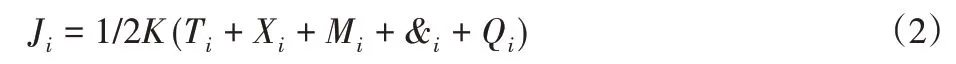
在算出柔性关节所受到的弹性势能后,本文还需要算出柔性多关节移动机器人末端动力学模型的整体电机能源大小与整体机械动力大小,在计算这两大数据时则需要应用具体的数学模型公式(3)来计算,具体的公式3如下:

式中:W、P—柔性多关节移动机器人末端动力学模型的整体电机能源与整体机械动力。对机器臂杆与柔性关节之间的轨迹进行计算,计算公式如下:

式中:G—机器臂杆与柔性关节之间的概念轨迹;g—机器臂杆与柔性关节之间的实际轨迹。只有柔性多关节移动机器人末端机器臂杆与柔性关节的参数G与g彼此之间的轨迹差异介于1~100之间时,才说明本文所建立的柔性多关节移动机器人末端动力学模型符合标准[8]。机器人末端的运动在方向力度上存在一定的误差,会直接影响机器人的运动体验[9-10]。本文通过建立机器人末端运动误差模型,降低机器人末端运动出现错误事件的发生[11]。信号对机器人关节点之间角度的影响线形图,如图1所示。
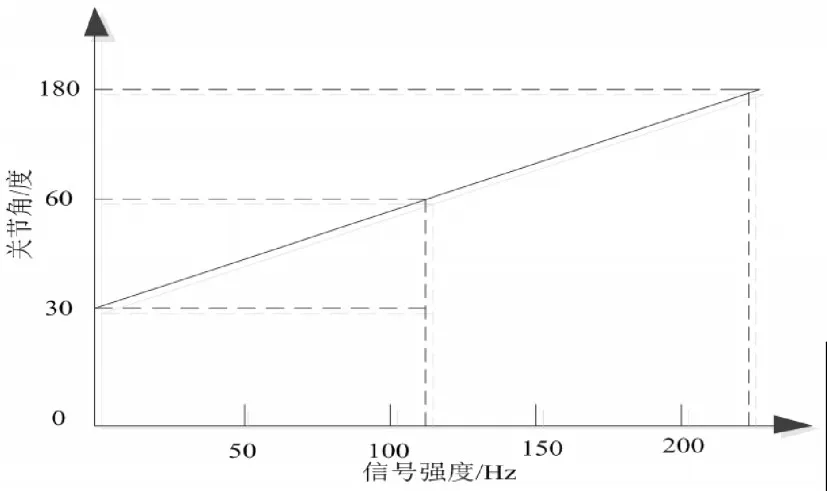
图1 信号与关节点之间角度线形图Fig.1 Angular Line Diagram Between Signal and Joint Point
根据图1的线形图确定本文通过H-D参数法对机器人末端运动关节间位姿误差进行计算,根据位姿误差推导出机器人末端运动的误差模型。H-D参数法是在机器人各个末端关节点上设置虚拟坐标系,然后用多阶矩阵表示没两个相连接的末端关节的空间关系。设置一个末端关节点,周围关节点参数为a1、b1、c1、d1,具体参数公式如下所示:
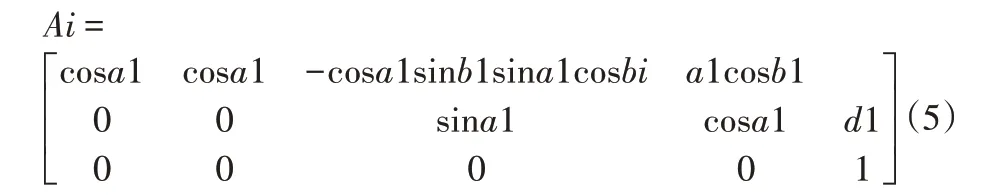
式中:d1—末端关节点变量;其余三个参数为可变几何参数,a1—机器人末端的长度;b1—机器人末端方向偏置角;c1—末端运动的运动角,具体参数坐标系示意图,如图2所示。

图2 机器人末端运动关节点虚拟示意图Fig.2 Virtual Representation of Moving Joint Points at the End of Robot
分别带入一个机器人末端运动的各个参数,如果Ai的值与设定的指标值相对误差在0.05以内,都认定此时的机器人末端运动不存在误差;如果超出指标就认为存在位姿误差[12]。根据机器人运动末端关节点位姿误差,将D-H参数算法中各个参数值进行单一替换,分别联立四个方程,计算出最终的柔性多关节移动机器人末端运动误差模型[13-14]。
3 柔性多关节移动机器人末端残余振动控制
DETMAX算法的优势在于能够辨识尺寸较大雅比克矩阵,根据测量姿态设计相应的行块促进形成新的矩阵,且计算结果稳定而又准确,以DETMAX算法为基础,选择末端的测量姿态,根据末端测量姿态判定结果实现振动控制。本文采用可观性计算方法,计算姿态组中各姿态的客观性指数,其选取步骤如下所示:
(1)从姿态组T1中随机抽取若干个测量姿态最为初始测量姿态,并采用DETMAX算法筛选。
(2)向初始姿态中逐一增加测量姿态,计算出最大化姿态。
(3)剔除最大化姿态保留最小化姿态。
(4)计算姿态的可观性指数,当数值到达一定数值时终止。
(5)最后选取最小化姿态并画出其变化规律。
在定义变量时,分别计算候选测量姿态、候选测量姿态数量、最小姿态的数量。当机器人处于增加姿态时,从测量姿态集合中随机抽出n个姿态,逐一增加测量姿态在算法中加入比较模块,从中找出最大化姿态;当机器人处于剔除姿态时,将抽取出的姿态剔除最大化姿态,形成新的姿态组T3,使姿态满足最小化姿态。若最终剔除后的最小测试姿态集合的可惯性指数满足数值大于1,则表示姿态可选取,若不满足将返回上一级重新剔除[15]。同时匹配内部操作参数,不断查找内部处理数据并构建内部数据关联结构。
利用优化界面调节实验优化数值,将各类参数数值提升至系统临界值中,判断不同数值间的差异,并将差异信息记录。时刻监管记录的信息状态,当产生异常状态时及时作出数据反应[16-17]。分配目标操作敏感度数据,在产生数据敏感信息时及时作出数据管理操作。将机器人运行速度数据记录在控制系统平台中,并时刻检验平台中的信息内容[18]。标记信息内容数据,按照数据空间的内部信息挑选对比检验参数。简化对比步骤。
设置中心调控空间整合检验参数,优化空间信息,主导外部实验环境空间调配装置,根据机器人运行速度信息获取其均匀性控制状况,实现控制[19-20]。
4 实验研究
为了验证柔性多关节移动机器人末端残余振动控制的有效性,设计对比实验。选用的实验对象为第二代五自由度柔性关节轻型机械臂,机械臂结构如图3所示:

图3 第二代五自由度柔性关节轻型机械臂结构Fig.3 Light Manipulator Structure of the Second Generation Flexible Joint with Five Degrees of Freedom
令五自由度柔性关节机器人在笛卡尔空间下自由运动,沿X方向和Y方向的行驶轨迹为正弦曲线,在Z方向静止不动,分别选用基于状态观测器的鲁棒反步控制方法、基于干扰观测器的控制方法以及本文提出的基于参数分析的控制方法对机器人末端残余振动进行控制。基于干扰观测器的控制方法内部控制器参数如表1所示:

表1 干扰观测器的控制方法内部控制器参数Tab.1 Internal Controller Parameters of The Control Method of the Disturbance Observer

分别记录三种方法跟踪下的控制误差,记录位置跟踪结果,记录结果,如图4所示。

图4 笛卡尔坐标系上的X方向与Y方向位置跟踪结果Fig.4 X Direction and Y Direction Tracking Results on the Cartesian Coordinate System
根据上图得到位置跟踪误差,如图5所示。

图5 跟踪误差实验结果Fig.5 Experimental Results of Tracking Error
从上图可以看出,本文提出的基于参数分析的控制方法对于控制误差的改善效果优于传统的两种控制方法。本文提出的控制方法使用一节积分滤波器对虚拟控制输入导数进行估计,分析传感器内部的噪声和输入信号,通过滤波处理改善动态性能。能够综合跟踪精度和阻抗控制性能两种要素,在确保跟踪精度的前提下,提高阻抗性能。而传统方法很难综合上述两种因素,因此导致的跟踪效果较差。
在研究跟踪误差后,探究机器人在不同控制方法下的柔顺性,操作器末端机械的空之轨迹为圆形轨迹,设置一个圆柱形的障碍物,障碍物示意图,如图6所示。
观察图6可知,机器人的运行轨迹为X-Y平面的圆弧运动,圆弧直径为300mm,由于加入了障碍物,计算机器人在切线运动下的期望接触力和期望保持力,探讨在受到障碍物阻力后,机器人的柔顺性。机器人在受到障碍物阻力后的控制参数,如表2所示。

表2 机器人控制参数Tab.2 Robot Control Parameters

图6 障碍物示意图Fig.6 Diagram of Obstacles
根据上述控制参数进行实验,得到不同控制方法下机器人的运行轨迹,如图7所示。
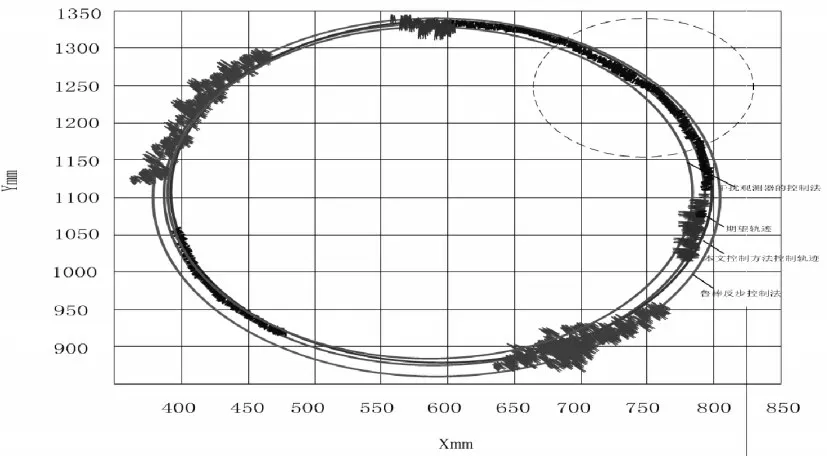
图7 控制轨迹示意图Fig.7 Diagram of the Control Trajectory
根据上图可知,本文研究的控制方法在接触各个不同的关节时,过渡状态十分平稳,不会出现抖动现象,而传统的控制方法在接触不同的关节时,过渡状态不稳定,且会出现抖动。
5 结束语
本文在传统控制技术的基础上,设计一种新的柔性关节机器人末端残余振动控制方法,结合模型建造技术与内部方程式管理操作,提升控制设计的有效性,并强化收集数据的科学性,便于后续实验研究的开展。实验结果表明,本文研究的控制方法能够有效控制机器人运行轨迹,确保机器人运行的柔顺性,适用于机器人实际控制操作。
