孤岛微电网下并联逆变器的二次控制研究

葛家宁， 董学育， 朱建忠

(南京工程学院 电力工程学院，江苏 南京 211167)

0 引 言

随着可再生能源不断被开发和各种传统能源资源紧张问题的日益严峻[1]，将清洁能源安全、方便和稳定地输送到用户侧，已成为国内外研究的焦点。逆变器是电力转换的一个重要器件[2]，能将直流电能转换成定频定压或调频调压交流电。在电网中，多个逆变器共同作用，造成了逆变器并联的局面。因此，对逆变器并联运行的研究一直是倍受关注的[3]。

逆变器的控制方法如集中控制、主从控制和分散逻辑控制，需要通信线进行信息的交换。虽然其控制方式简单，控制效果较好，但同样也增加了系统的成本，降低了系统的可靠性和稳定性。而下垂控制则不需要通信线，且冗余度好、可靠性高、动态性能好，已成为目前研究的重点。

传统的下垂控制也有一定的缺陷，比如逆变器的总输出阻抗难以和其额定容量匹配，传统的下垂控制策略就很难实现各个并联逆变器输出功率的准确分配[4]。因此，有学者提出在控制环节中加入虚拟阻抗，来平衡各个逆变器输出的阻抗，这个方法起到了很好的效果。

但是，在下垂控制中加入虚拟阻抗，使电压和频率的降落增大，加之下垂控制本身对电压和频率的“下垂”作用，使得电压和频率偏离允许的电压范围。为了改善这一情况，本文介绍了一种二次控制的方法，并通过MATLAB/Simulink搭建的仿真模型验证了新型控制方法的有效性和可行性。

1 下垂控制的基本原理

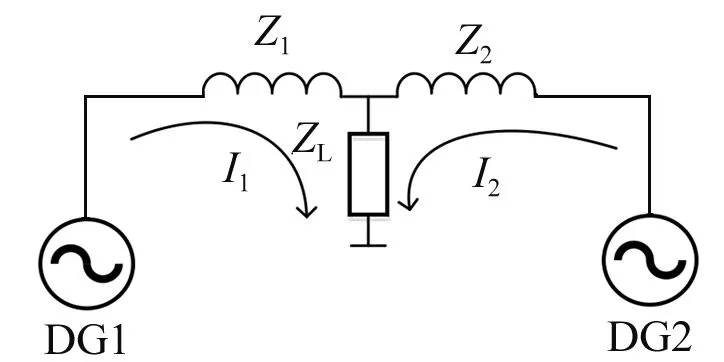
图1 两个逆变器并联运行的结构图

图2 逆变器单相功率图

图1是两个逆变器并联运行的结构图。图1中：Z1和Z2分别为线路的阻抗；ZL为公共负载；I1、I2为两支路上的电流，由DG 1和DG 2共同为负载提供功率。

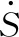
可求出图2中A点注入的复功率为：

(1)

(2)

(3)

式中:P和Q分别为逆变器输出的有功功率和无功功率；θ和δ分别为线路阻抗角和功率角。

根据式(1)～式(3)可以得出有功功率和无功功率的表达式为：

(4)

(5)

再令线路阻抗Zejθ=R+jX,式(4)和式(5)可以进一步改写成：

(6)

(7)

进一步地，可将其写成：

(8)

(9)

由于线路阻抗中X≫R，因此R可以忽略。同样，由于功率角δ很小，因此，sinδ≈δ,cosδ=1[6]。由式(8)和式(9)可以求出：

(10)

(11)

从式(10)和式(11)可以看出,功率角δ主要取决于有功功率P，电压差U1-U2主要取决于无功功率Q[7]。也就是说，通过对有功功率和无功功率的调整，频率和电压的幅值就能得到控制[8]。因此，有功/无功功率下垂控制可以写成：

f-f0=m(P-P0)

(12)

U1-U0=n(Q-Q0)

(13)

式中:f0、U0分别为参考频率和参考电压；P0、Q0分别为有功功率和无功功率的参考值；m、n分别为有功和无功的下垂系数。

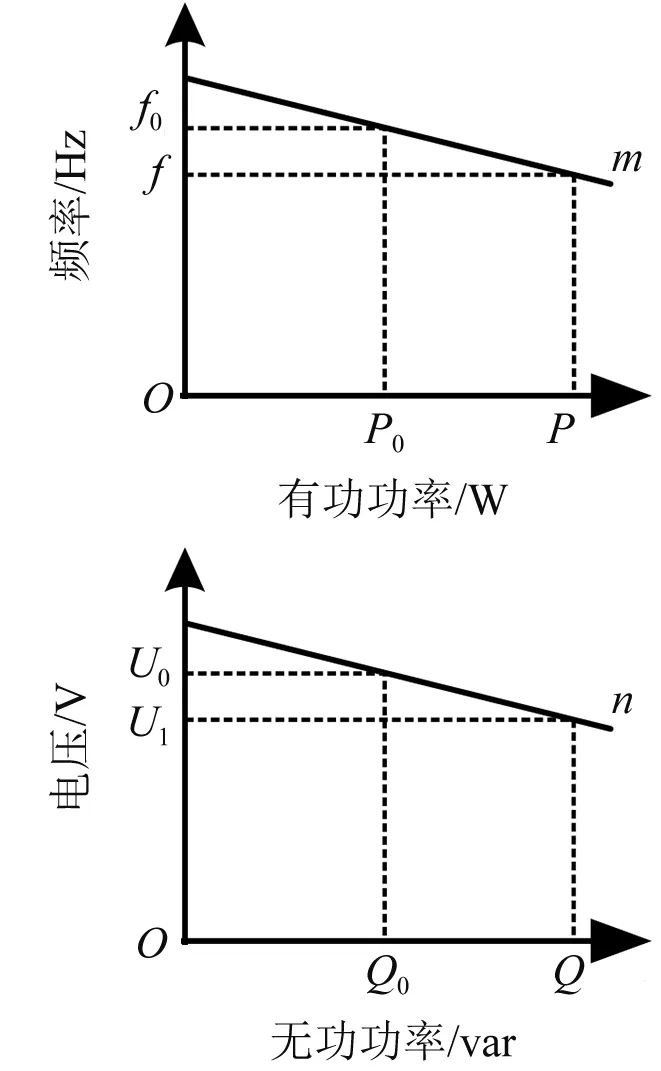
图3 频率-电压下垂控制特性曲线

频率和电压的下垂控制特性曲线如图3所示。从图3中可以看到，有功功率的调节会带来频率的升高或下降；无功功率的调节会影响电压的幅值，有功功率和频率与无功功率和电压之间存在着耦合的现象。除此以外，当线路呈感性时，有功功率和无功功率之间也会存在较强的耦合。虽然在理论分析中可以忽略，但是实际上是客观存在的。

因此，可以对以上的下垂控制做出改进。特别是在低压电力网络中，线路阻抗R是比较大的，约为感抗X的7.7倍，可以被忽略的不是R而是X。这时，调整有功影响的是电压的幅值，调整无功影响的是频率。

2 虚拟阻抗

在线路阻抗不匹配的情况下，传统的下垂控制不能实现并联逆变器之间无功功率的合理分配[9]，通常的做法是加入虚拟阻抗，使逆变器输出的阻抗近似相等。图4是加入虚拟阻抗后，系统的控制框图，其中ZD(s)是加入的虚拟阻抗的传递函数，输出电压可以表示为：

(14)

图4 虚拟阻抗控制框图

图5 逆变器输出阻抗等效图

图5是逆变器输出阻抗的等效图。通常情况下，ZD设计得比Z0大，因此总的输出阻抗取决于ZD。一般情况下，ZD取感性阻抗，虚拟阻抗的加入不会对功率的损耗产生影响，从而虚拟阻抗的选择比较灵活多变，能够改善逆变器的控制性能。系统中加入了虚拟阻抗后，逆变器的输出阻抗成为了一个新的变量，阻抗角θ=tan-1X/R,X和R是总阻抗的虚部和实部。

3 二次控制

虚拟阻抗的加入解决了阻抗不匹配的问题，使功率能合理地被分配，但是虚拟阻抗的加入也同样带来一些问题，比如对电压和频率的降落作用[10]，电压和频率的稳定对整个电力网络来说是至关重要的。因此，维持电压和频率的稳定是很有必要的。为了弥补电压和频率的偏差，本文在控制系统中加入二次控制，以保证电压和频率的偏差值接近于0。保证在负载变动时和逆变器投切过程中电压和频率的稳定性[11]。

图6是系统整体控制框图，整体的控制部分可以分为一次控制部分和二次控制部分。一次控制部分主体为下垂控制，一次控制基于对逆变器输出电压和电流的测量来计算有功功率和无功功率，为下垂控制和虚拟阻抗控制提供基础。而二次控制将利用外部的控制器来储存一次控制中产生的偏差。同时，为了使多个逆变器连接组成一个微电网，微电网的电压和频率需要被测量，并将其设定为二次控制的参考值[12]。

图6中的二次控制，其控制表达式可以写成：

(15)

(16)

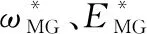
图6 系统整体控制框图

二次控制是为了确保微电网中的各项参数稳定在要求的范围内。除此以外，二次控制也包含了一个同步控制环，以确保多个分布式系统之间投切的平顺性[13]。二次控制是在一次控制的基础上，对一次控制产生的偏差进行修正，使系统的电压和频率的跌落降低到最接近0的状态。加入二次控制后，对电压和频率会有一个明显的抬升作用。

4 仿真分析

为了验证二次控制的效果，搭建Simulink逆变器并联模型，以两台逆变器为例，选取两台容量相同的逆变器，直流侧用800 V的直流电源等效。逆变器1的下垂系数是逆变器2的两倍，同样的，虚拟阻抗也是两倍的关系。设置运行动作，0～0.15 s,两逆变器并联运行，但只带本地负载运行。0.15 s时，合上开关，公共端接上负载，逆变器1和逆变器2共同为负载提供能量。逆变器1和逆变器2的本地负载都为5 kW+5 kvar，开关闭合后，公共端接上的负载为20 kW+20 kvar。模型的各项参数如表1所示。

表1 模型的各项参数

图7和图8分别是未加入二次控制时逆变器1的输出电压曲线和两个逆变器的频率曲线。从图7可以看到：电压在0.15 s后电压的幅值只能达到290 V，低于参考值311 V，降幅较为明显。图8中的频率在0.15 s后降到了49.82 Hz，降低的幅度也较明显。从图7和图8可以看到，开关未动作时，电压和频率都保持在一定的范围内，但是当开关闭合后，随着负载的增加，电压和频率的幅值也随之降低了。

图9和图10为加入二次控制后逆变器1的输出电压曲线和两个逆变器的频率曲线。从图9可以看到，加入二次控制后，虽然增加了负载，但电压曲线有一个快速的抬升过程，使电压的偏差降到了最小，相较于未加入二次控制时电压的偏差小了很多。而图10中，频率在0时刻开始就不断在修正，可以看到，在0.15 s时，频率有一个明显的降落，随后便不断被抬升，直到0.18 s时，超过50 Hz并上升到50.02 Hz，从0.19 s时开始，频率被降低至49.96 Hz，随后又被抬升。总体来看，频率被不断抬升或降低，但是不断接近50 Hz的基准频率，偏差越来越小。

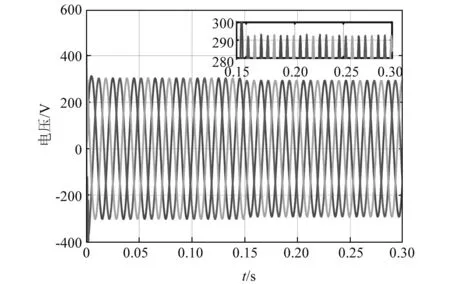
图7 未加入二次控制时逆变器1的输出电压曲线

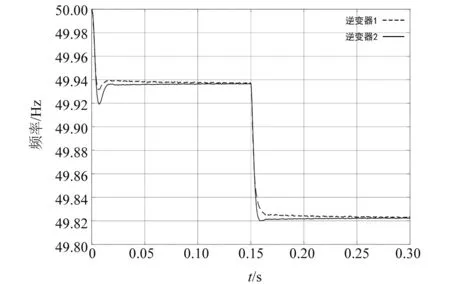
图8 未加入二次控制时两个逆变器的频率曲线

从以上仿真试验可以看到，二次控制的加入对于电压和频率的改善作用是明显的，对于整体系统的稳定性起了一定作用，仿真结果证明了二次控制是有效可行的控制算法。

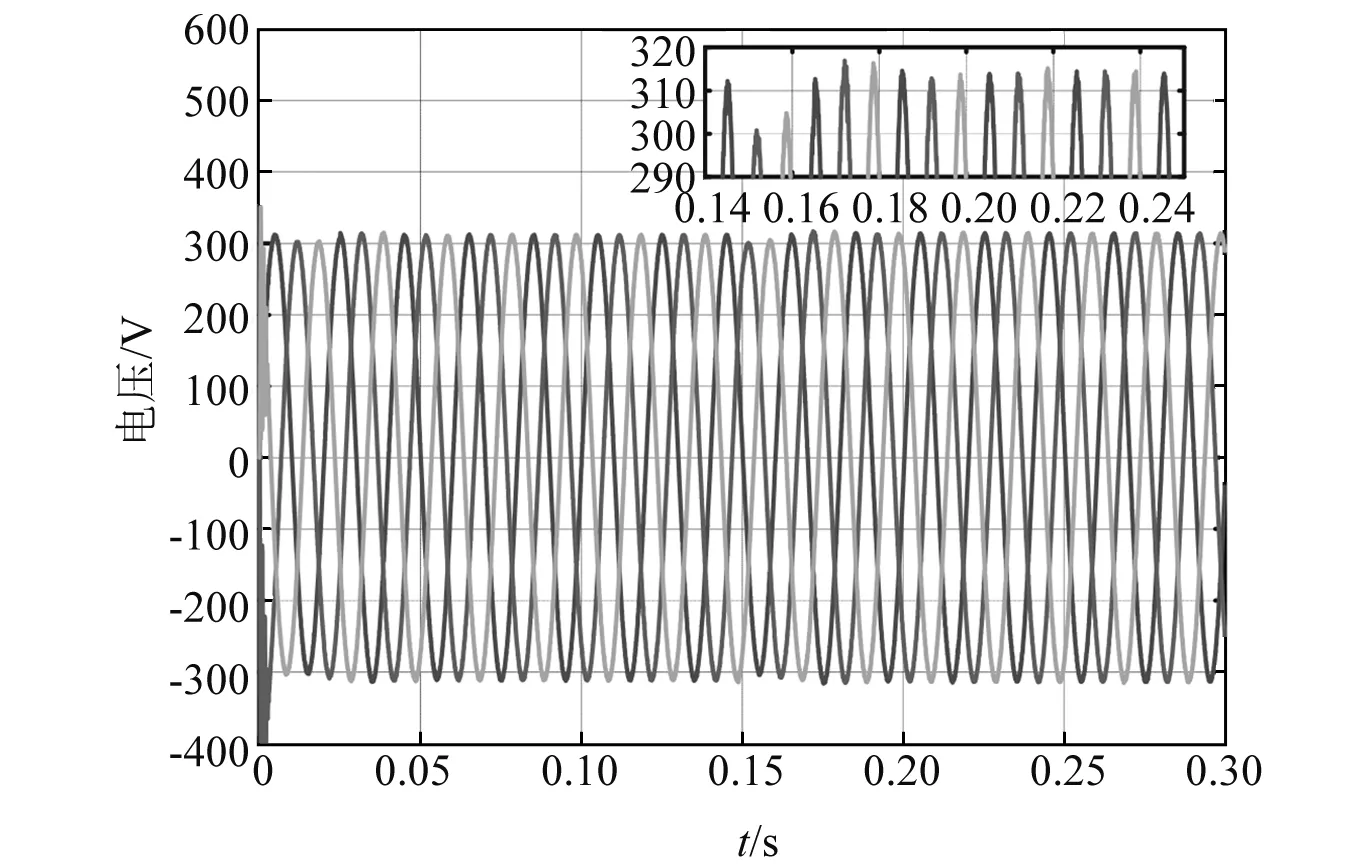
图9 加入二次控制后逆变器1的输出电压曲线

图10 加入二次控制后两个逆变器的频率曲线

5 结束语

下垂控制因其本身的固有缺陷，造成电压和频率的降落。并联逆变器在加入虚拟阻抗后，能够使得功率均分，但是电压和频率的降落更加严重。本文提出一种二次控制的算法，对电压和频率实现二次控制，使电压和频率恢复到理想状态。一次控制是在下垂控制基础上构建的环节，其包含了一个输出虚拟阻抗环。二次控制是对一次控制中产生的电压和频率偏差进行修正的过程，能使电压和频率恢复到最佳状态。本文搭建基于MATLAB/Simulink的并联逆变器模型，对加入二次控制前和加入二次控制后的电压和频率曲线进行对比分析。结果表明，加入二次控制后，基于下垂控制的并联逆变器在暂态时有更小的电压和频率跌落，稳态时能够接近额定值运行，仿真结果证明了二次控制的有效性和可行性。