基于适应度地形分析的进化计算研究综述

李亚欣，梁 静，岳彩通，李 珂

(郑州大学 电气工程学院，河南 郑州 450001)

随着大数据时代的到来，数据挖掘和机器学习成为研究热点。具有多模态、含约束、多目标等性质的复杂优化问题因其具有更高的理论和实际应用价值被人们持续研究。为了解决这些优化问题，早先搜索策略的设计通常需要依赖算法设计者的经验、待优化问题的先验知识或调参确定。虽然研究人员设计了多种基准测试函数集以尽可能涵盖优化问题的更多属性，但是并没有从根本上解决这个问题。根据“无免费午餐”定理[1]，一种算法不可能在所有问题上都表现优异，不同的算法可能在不同类型的问题上有特定优势。因此，需发展基于学习的方法来自适应地根据优化问题的多方面需求和性质指导算法选择和种群进化。

问题的适应度空间地形能直接反映问题的特性，因此提取地形信息有助于问题的特性分析。适应度地形的概念源于理论生物学[2]，它是指一个三元组L=(S,V,F)，其中S是所有解的集合，V：S→2s是一个特定的邻域函数，对于每一个s∈S，V(s)是其邻域解集，F：S→R是适应度方程。适应度地形的作用是与优化问题的真实地形对比，以便我们了解算法的工作原理，更好地解决实际问题[3]。适应度地形分析(fitness landscape analysis，FLA)是指数据驱动技术的集合，用于提取与适应度地形特性有关的描述性或数值度量[4]。因此，FLA的目的是获得有关给定优化问题的知识，并深入了解对于算法性能至关重要的优化问题的特征[5]。

进化计算(evolutionary computing，EC)通过模拟自然界生物进化机制，在一些可行解组成的种群中，通过迭代进化寻求最优解。EC技术因其强大的全局搜索能力和并行计算能力备受关注，最近更是广泛应用于适应度地形的研究。然而，现有文献对近些年EC在适应度地形上的研究缺乏全面而系统的讨论。基于此，本文对EC在适应度地形分析方面的相关文献进行分析和总结，为相关研究人员提供参考。

1 进化计算

1.1 进化计算的主要特点和分类

进化计算是模拟生物进化理论而形成的一种全局优化自适应概率搜索的算法理论，它是计算智能的子域之一，是一类具有启发式或随机优化特点的求解器。它受生物进化中适者生存、优胜劣汰自然选择机制和遗传信息传递规律的启发，通过程序迭代模拟这一过程，在一些可能的解组成的种群中，通过自然演化寻求最优解[6]。进化计算一般包括种群初始化、个体适应度值评价、种群繁殖与进化等，其基本的计算流程框架如图1所示。

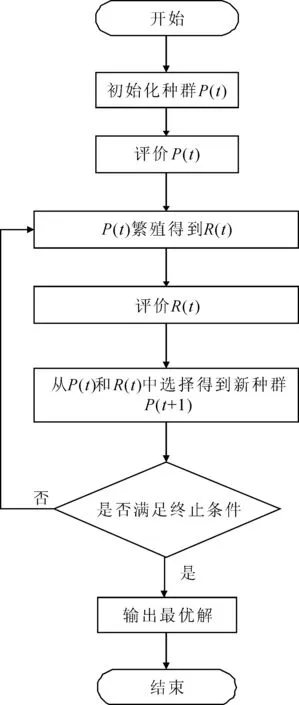
图1 进化计算的基本流程框架

与普通搜索算法一样，进化计算也是一种迭代算法。不同的是，在最优解的搜索过程中，普通搜索算法是从某一个单一的初始点开始搜索，而进化计算是从原问题的一组解出发改进到另一组更好的解，再对这组改进的解进一步改进。而且，进化计算还适用于没有解析目标函数和无法得到目标函数梯度信息的优化问题，以及在解决同时有整数和连续变量的混合优化问题方面具有显著优势。

进化算法是一种理想的全局搜索方法，它有以下几个特点：(1)有指导搜索，搜索中利用个体目标函数值的信息，而不必用目标函数的导数信息或与具体问题有关的特殊知识来指导种群进化；(2)自适应搜索，通过进化算子进化操作来改进群体性能；(3)渐进式寻优，逐代进化；(4)并行式搜索，对每一代群体中的个体同时进行搜索，也适合于并行计算；(5)黑箱式结构，只需要研究输入和输出而不需考虑过程；(6)全局最优解，在整个搜索区域的各个部分同时进行搜索行为；(7)鲁棒性强，处理不确定性有优势，因为进化算子中多包含随机因素，与确定性算法相比，其具有较好的鲁棒性。

常用的进化计算方法主要包含以下几种：(1)遗传算法[7](genetic algorithm, GA)。GA是一种自适应优化概率搜索算法,它通过借助遗传学原理，经过自然选择、遗传、变异等作用机制进而筛选出具有适应性更高的个体；(2)遗传规划[8-9](genetic programming, GP)。GP是一种用于求解最优解结构的优化算法，而这种解的结构一般用树状图来表示；(3)进化规划[10](evolution programming, EP)。EP是一种模拟生物进化过程与机制求解问题的自适应进化算法,它通过繁殖、变异、竞争、选择4种操作来产生新一代种群；(4)进化策略[10](evolution strategies, ES)。ES是一种模拟自然进化原理以求解参数优化问题的优化算法,它利用遗传信息每一代的传承变异，通过适者生存的理论，保存适应性强的个体，得到最优解；(5)粒子群算法[11](particle swarm optimization, PSO)。PSO算法是受鸟类群体觅食行为的启发而提出的一种仿生优化算法,它利用种群粒子间合作与竞争来指导优化搜索[11]；(6)差分进化算法[12](differential evolution, DE)。DE算法是一种具有保优思想的贪婪遗传算法，它通过随机生成初始种群，利用变异与交叉操作来选择最佳个体进行繁殖；(7)蚁群算法[13](ant colony optimization algorithm, ACO)。ACO算法是受蚂蚁觅食行为的启发而提出的一种启发式搜索算法,它模拟蚂蚁寻找食物的规律，在运动过程中以信息素为牵引，控制蚂蚁寻找最优路径。

1.2 进化计算的理论基础研究

一般来说，进化算法的求解包括以下几个步骤：给定一组初始解，评价当前这组解的性能；从当前这组解中选择一定数量的解作为迭代后的解的基础；再对其进行操作，得到迭代后的解；若这些解满足进化要求则停止，否则将这些迭代后的解作为当前解重新操作。目前，有关进化计算的理论基础研究主要包括以下几个方面：

第一，进化计算在算法的复杂度、收敛性和收敛速度分析等方面的数学建模和理论研究。例如，Huang等[14]针对连续型进化算法，提出了一种基于平均增益模型的时间复杂度上界的估算方法，建立了理论基础与实际应用的沟通桥梁。覃俊等[15]基于有限马尔可夫链理论，提出了一种多目标进化算法(multi-objective evolutionary algorithm，MOEA)的收敛性分析框架。案例研究的结果表明，搜索算子和选择算子不仅对提高MOEA的效率有重要作用，而且对算法的收敛性也有很大的影响。Zhang等[16]进行有关算法行为和收敛性的理论分析，并证明稀疏性促进算法如何快速逼近一个局部最小值。Wu等[17]利用离散时间动态系统理论对粒子群算法进行了收敛性分析和参数选择，该研究为一般性随机算法的参数选择提供了定性指导。

第二，从理论和实际效果两方面比较进化算法与其他优化方法的不同。例如，Del等[18]结合稳态和经济标准，将增强型粒子群算法(enhanced particle swarm optimization algorithm，enhanced-PSO)的性能与经典优化方法进行了比较以说明进化算法的有效性。Piotrowsk等[19]将多种进化算法训练注入噪声的多层感知器神经网络，用于估计河流中的纵向弥散系数。实验结果显示，与之前最常用的基于梯度的优化方法相比，进化算法不仅能够应对不可微问题，并且能快速收敛到局部最优。另外，Zhang等[20]也充分利用进化算法的全局搜索特性和反向传播算法的局部搜索功能，提出了一种三层前馈神经网络的两阶段训练算法。通过对比传统的剪枝优化等方法，该算法可以以较低的计算成本获得更好的泛化能力。

第三，从生物进化或自然界各种现象中获得新启发，提出新方法，或对现有的进化计算方法进行改进。例如，Schaffer[21]首次提出多目标遗传算法，随后多种多目标遗传算法NSGA[22]、NSGAII[23]等被相继提出。自从多目标粒子群优化算法被首次提出后[24]，后期也出现了多种多目标粒子群优化算法，代表性算法包括NSPSO[25]、MOCLPSO[26]、MO_ring_PSO_SCD[27]等。此外，针对多模态多目标优化问题需要优化算法来定位多个帕累托解集的情况，Liang等[28]提出了一种基于聚类技术和精英选择机制的差分进化算法来获得决策空间和目标空间中均匀分布的解集。针对全局解决方案不可行的问题，Yue等[29]提出了一种利用小生境方法的多模态多目标遗传算法来查找全局和局部帕累托解，使种群可以在局部范围内快速进化。

第四，研究如何通过学习提高进化算法自适应求解能力。例如，Peng等[30]提出了基于种群的算法组合方案(population-based algorithm portfolios，PAP)，通过将总种群划分为多个子种群以及为每种算法分配一个子种群，多个种群之间信息交互来实现时间预算的分配，并在文献[31]中进行了相关拓展与改进。为了实现利用合适的策略和控制参数来解决不同类型优化问题或适应不同演化阶段的目标，Fan等[32]提出了一种基于知识的策略自适应和控制参数的环境优化算法。该算法利用学习遗忘机制实现了对变异和交叉策略的自适应调整，在所有比较算法中具有很强的竞争性。针对多目标问题搜索空间中搜索冗余的情况，Huang等[33]提出了一种结合适应度地形崎岖度和强化学习策略的多目标差分进化算法。实验结果表明，该算法可以缓解搜索冗余和搜索空间映射不平衡的问题，有效提高了算法在优化过程中的收敛性。另外，尽管目前已经提出了多种DE算法来解决各种优化问题，但是并没有发现任何一种DE算法在多种类型的问题上都表现最佳。于是，Shao等[34]提出了一种基于适应度模态检测(landscape modal detection, LMD)技术的自适应地形模态检测(DE-LMD)算法。针对不同地形的问题，采用了包含DE/current-to-best/1和邻域引导变异的混合变异策略。实验结果表明，该算法在不同类型的优化问题上都具有良好的性能。

通过大量的文献调研发现：国内外将进化算法用于研究优化问题本身特性的研究相对较少，而将适应度地形应用于进化算法受到了大量学者的广泛关注。图2给出了Engineering Village数据库中2000—2020年适应度地形相关文章数的变化趋势及相关文章中中国占世界文章数目的比例。由图可见，相关文章数总体趋势逐渐增长，2008—2015年整体有所下降，但2016年开始回升并达到历史最高，可见适应度地形分析目前是研究的热点。

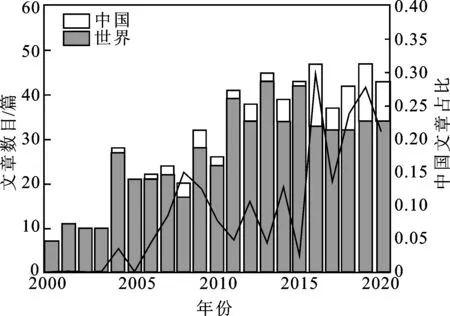
图2 2000—2020年基于适应度地形分析的进化计算研究的相关文章数目趋势图

2 适应度地形分析

2.1 适应度地形的定义

令X为适应度函数f的候选解，使得Y=f(X)。候选解的子集为输入样本x，其成本值为输出样本y。对于未知特性的优化问题，只能通过对决策空间进行采样获取问题的特征信息。搜索算法保持了候选解与计算代价关系的简化模型，该模型假定问题具有可利用的结构，因此进化算法可以通过在运行期间收集信息来推断有关问题结构的详细信息，这种结构被称为函数的适应度地形[35]。

图3显示了一个维数为2的函数适应度地形图，其中图3a说明该地形是由山脊、山谷、高原和盆地组成的三维表面。局部和全局最优值均位于此曲面的最低点[36];图3b显示了适应度地形的等高线图,颜色条显示的是高度值。在这种情况下，搜索算法的目标是找到最优解，并在表面更新模型时存储有关表面结构的信息，而这种利用模型推断适应度地形情况的方式直接影响算法的搜索性能。

图3 D=2的函数适应度地形图

2.2 适应度地形的基本特性

2.2.1 模态性与平滑度 可以使用全局最优个数xg和局部最优个数xl来描述适应度地形的某些特征。单模态函数被定义为|xg|=|xl|=1的地形(如图4a)，而多模态函数可定义为|xg|=|xl|>1的地形(如图4b)。

与模态性紧密相关的特性是平滑度[37]，它是根据在邻域范围内代价函数适应度值变化的幅度，将适应度地形正式分为崎岖、平滑或中立。崎岖的地形[38]是指在一定的邻域范围内候选解的适应度值有很大的波动，呈现多个局部最优值，以及地形呈现陡峭的上升和下降(如图4c)。中性的地形[39]具有较大的平坦区域，其中输入变量的变化无法产生输出的显著变化(如图4d)。由于崎岖和中性地形的特性，因此很难断定地形的某些区域是否值得探索。全局结构是指由聚类的局部最优值xl组成的整体盆地形状，可用于指导对全局最优点xg的搜索。如果该结构是平滑的(如图4e)，则将为算法提供潜在的可利用信息。如果这种模式是崎岖的或不存在的，那么找到一个全局最优值是具有挑战性的或者是找不到的。另外，也有可能发现表现出欺骗性的问题，即全局结构和梯度信息使算法偏离最优值(如图4f)，从而使优化算法的效率不如随机搜索或穷尽枚举[40-41]。

图4 描述特定地形特征的6个一维函数适应度地形图

2.2.2 吸引盆地 除了局部最优个体的数目外，盆地大小的分布和深度是确定地形难度更为重要的因素[42-43]。其中，具有相对较小吸引力盆地的局部最优区域被称为孤立的地形。盆地的大小和深度不仅会增加分析优化算法适应度地形的复杂度，而且会对种群个体的更新产生重要影响。Whitley等[44]研究了模态性对遗传算法性能的影响，发现尽管局部最优值的数目并不总是会影响遗传算法的行为，但高度合适的局部最优值(尤其是具有大吸引力的盆地)确实为遗传算法搜索带来了问题。另外，Kinnear等[45]也发现，在使用遗传规划算法解决问题时，地形盆地的深度与一系列问题的难度呈现良好的相关性。

2.2.3 对称性 适应度函数或地形中的对称性会产生多个具有相同适应度值的点，因此有多种方式能将搜索空间划分为较大的等价类。例如，如果适应度地形相对于其中一个轴对称，则称为轴向偏置。如果在设定距离值上，某些点与最佳点的适应度值相同，则无论点的方向如何，适应度地形都相对于最佳点对称。对称性对算法搜索的性能存在相互矛盾的研究结果:Whitley等[46]在研究中发现函数对称性的存在会导致某些遗传算法的失败；Naudts等[47]的研究也表明，对称性的存在会对简单遗传算法的收敛能力产生负面影响，这可能是由于两个互不相同的良好(对称)解相互交叉导致了不好(不对称)的子代。但是，其他研究表明，遗传算法确实在具有轴向偏差的适应度地形上表现出更好的性能[48]，并且对于此类问题，坐标系的旋转会导致严重的算法性能损失[49]。

2.2.4 进化性/搜索性 进化性可粗略地定义为进化能力[50]。Altenberg[51]将进化能力描述为种群产生比其父代更好的子代的能力。尽管可进化性的概念与算法种群进化的能力有关，但就特定的搜索算子或策略而言，它也可被视为适应度地形的特征。本文将这种可进化性定义为给定搜索过程中采样点向适应度更好的地形中某个位置移动的能力，即可搜索性。该定义扩大了可进化性的范围，超出了基于进化算法的范围，以涵盖任何搜索过程。可搜索性是问题的特征，仅对特定搜索策略有意义。另外，对某一种算法而言，具有高搜索性的问题，相对于另一种算法可能表现出低搜索性。近年来，关注于可搜索性的适应度地形分析技术包括适应度进化描述[52]、适应度云[53-54]、适应度概率云[53,55]、负斜率系数[54]、累计逃逸概率[55]等。

2.2.5 上位性 在遗传学中，上位性是指染色体中基因之间表达的依赖性程度。如果基因独立地影响染色体的整体适应性，那么该系统的上位性就很低。如果基因的适应性贡献取决于其他基因的值，则该系统就具有较高的上位性。通常，对于优化问题，此特性可以称为变量之间的相互依存度(也可称为非线性可分离性)。当优化问题中的变量相互依赖时，这意味着不可能做到通过调整一个独立于其他变量的变量来找到最优值[48]。例如，如果适应度函数的数学表达式中不同变量可以通过加法分开，则可以认为变量是独立地对适应度值做贡献。但是，如果在函数表达式中是通过乘法将不同的变量组合在一起时，这些变量就必须配合才能有助于提高适应度；如果任一变量的值较低，那么即使另一个变量的值较高，乘积也可能比较低。研究表明，对遗传算法而言，线性可分离函数比非线性可分离函数更容易求解[47]。

2.3 基于适应度地形分析的进化计算研究

2.3.1 地形特征的设计与改进 尽管许多适应度地形分析技术最初被定义为精确测度，但实际上它们被用作近似度量[3]。由于我们的目标不是将技术划分为各种类别，而是为了了解实际使用的技术，因此为了更具描述性地区分特征，表1对代表性适应度地形技术进行了描述和说明。其中，与模态性和全局结构相关的技术包括适应度距离相关[6,56]、色散度量[57]；与崎岖性和中立性相关的技术包括自相关函数[58]、相关长度[59]、随机游走[60]、熵测度[61-62]、盆地规模比[63]等。近年来，关注可搜索性的适应度地形分析技术包括适应度进化描述[52]、适应度云[53-54]、适应度概率云[53,55]、负斜率系数[54]、累计逃逸概率[55]等。并且，量化上位性与欺骗性的技术有按位上位性[64]、上位性差异[65]和信息地形[40-41]等。

表1 代表性适应度地形分析技术

在进化计算领域，许多研究人员基于这些代表性的适应度地形特征，进行了针对性的改进。例如，Lunacek等[66]研究了色散度量的性质。为了改善色散度量的缺陷，作者对3个基本方法提出了3个独立的修改，分别是色散边界的标准化、分数p的LP范数和固定步长的随机游走。实验结果表明，这些改进可以促进收敛并增加问题的可分离性。此外，Ochoa等[67]提出了一种将组合优化问题的基本地形特征压缩为局部最优网络图形的技术，而这种基于图的模型可用于表征地形结构和局部最优值的分布。Vanneschi等[68]也指出负斜率系数原始定义的限制，于是为负斜率系数提供了一个新的相关定义和提出了一种划分适应度云的新方法，并从经验上证明了此新定义作为问题硬度度量的适用性。

2.3.2 利用地形特征对优化问题分类 适应度地形分析是一个涵盖理论和实践技术的术语，用于分析与问题难度相关的特征，不同的搜索运算符如何影响适应度地形拓扑等。利用地形特征对优化问题分类可以帮助选择适合于解决待优化问题的良好算法。近年来，针对优化问题的分类，学者们做了许多工作。Cicirello等[70]研究了可用于排列的距离度量，并使用主成分分析对现有特征分类，从而识别与优化问题最相关的搜索算子。Kerschke等[71]通过引入检测优化问题漏斗结构的特征，将其与现有相关特征组合在一起，以便于对有关漏斗属性的优化问题进行分类，并在文献[72]中进行了拓展和改进。Merz等[73]对二次分配问题的多个实例进行了适应度地形分析，并根据问题实例的硬度特征对优化问题的实例进行分类。基于此，可以找到重组和/或变异操作算子的有利选择以更好地解决待优化问题。

2.3.3 利用地形特征指导算法设计 随着进化算法的不断发展，适应度地形可以在适应度方面提供更丰富的特征信息，从而更好地指导研究人员设计有效算法。这些地形特征分别从不同角度反映了优化问题最优解的分布、数量以及全局拓扑。例如，对于每种算法仅适用于某个适应度地形的情况，Li等[74]提出了一种新的自反馈差分进化算法，通过提取各代种群中局部适应度地形特征，并结合各个局部适应度地形中单峰和多峰的概率分布，选择最优的变异策略以此来自适应地解决某些类型的优化问题。Sallam等[75]在差分进化算法选择机制的设计中也使用了优化问题的地形信息，针对组合约束优化问题，提出了一个具有适应距离相关性的多算子DE框架，该框架用于在进化过程中动态地将更多权重分配给性能最佳的DE算子。实验结果表明，与现有算法相比，该算法能够产生高质量的解决方案。另外，Kuk等[76]提出了将适应度地形分析技术和自适应算子选择机制相结合的多目标算法框架，该方案扩展了适应度地形分析收集的可搜索性和多模态信息，是将适应度地形应用于多模态多目标问题的初步研究。

2.3.4 利用地形特征评估算法相对性能 群集智能的研究重点主要在算法方面，目前对于优化问题以及与问题相关的算法行为的研究相对较少。并且，当文献中提出新算法或现有算法的变体时，很少讨论或分析算法弱点以及算法失败的原因。适应度地形分析是一种可用于分析优化问题的方法，根据适应度地形特征来表征问题，可以研究问题类型与算法性能之间的联系。例如，了解和研究算法性能的边界对于良好的实践研究至关重要，并且可以提供对算法优缺点更为准确、更强大的描述。于是，Smith等[77]设计了一种能够评估各种优化算法相对能力的新方法，即将一组不同实例表示为高维特征空间中的点，而且，投影到低维空间以可视化。定义了评估算法好坏的性能指标，并提出了一种用于测量算法占用空间大小的方法。另外，Malan等[78]研究了多种地形特征用来分析算法进化过程，并表明最初针对离散优化问题提出的许多现有的适应度地形分析技术同样适用于某些连续优化问题。实验表明，没有任何一种度量能够单独用作PSO算法的预测指标，但是可以结合多种适应度地形特征来预测PSO算法的失败。Tavares等[79]也研究了启发式算子和遗传算子之间的相互作用如何影响解决多维背包问题的进化算法的搜索性能，并且对启发式算法和局部搜索技术如何提高进化算法的性能进行了对比分析。

续表1

2.3.5 利用地形特征指导算法选择 近年来，不同类型的进化算法层出不穷，并且在不同类型优化问题上的表现截然不同。因此，工程师们很难选择合适的方法来有效地解决目标问题[80]。对于待优化问题来说，最直接的一种方法是分别执行所有可能的算法，然后选择表现最佳的算法。尽管这对于某些实际应用而言是一种合理的离线优化方法，但是为每个待研究问题找到最佳参数的代价十分昂贵。在这种情况下，算法推荐系统应运而生。Kerschke等[81]构建了一组具有代表性的高性能互补求解器，并提出了一种算法选择模型。与单个最佳求解器相比，该算法选择模型仅需要不到一半的资源就可以解决给定的问题。除此之外，Abell等[82]也基于公认属性及适应度地形特征提出了一个算法选择模型，并将BBOB问题集用于特定实例的算法配置模型中。实验证明，该模型能够在特征计算过程中为未知实例选择最快的求解器。另外，Bisichl等[83]将算法选择任务视为基于探索性景观分析的成本敏感的分类任务，通过对可行集上的函数进行系统采样获得的低级特征来预测给定组合中性能良好的算法。

3 问题与展望

3.1 问题

虽然进化计算在适应度地形特征分析方面取得了很多成果，但是由于待优化问题的复杂性，目前现有的算法及方法在实例生成问题、高维问题、特征提取、算法配置、知识运用等方面仍存在不足，距离广泛的工业应用存在明显的差距，尚有许多研究工作有待深入开展。

3.1.1 演化生成问题及实例 与可以自动综合数据集的组合优化问题不同[84-85]，连续优化问题通常由难以任意生成的复杂函数表示，这些函数的适应度值易于获得并且可以直接反映问题的特征。由于实验中缺少现实世界中的连续优化问题，因此为了提供一种更系统的方法来对基于采样的优化启发式方法进行测试，研究者们将多种基准测试函数集合在一起，例如，BBOB问题集[86]、COCO问题集[87]、WFG问题集[88]、CEC竞赛问题集[89-90]等。但是，对于算法推荐与分类任务来说，这些函数集不足以评估元启发式方法的性能，因此难以基于如此少量的样本来训练有效的分类器。更重要的是，现有的基准测试问题由数量有限的映射函数组成，这些函数无法为不同的元启发法提供足够多样的困难度，从而产生效果不均衡的数据集，这对推荐模型的训练有害。

3.1.2 适应度地形特征的维数灾难 形式上，函数f的适应度可表示为一个三元数组L= (X,f,d)，其中X是适应度函数f的候选解集，d是用于量化候选解之间相似度的距离度量。在连续优化问题中，d通常是欧氏距离。这些元素构成一个邻域结构Nr(x)∈X，其定义如下:

Xi∈Nr(x)↔d(x,xi)≤r,

(1)

其中r是以xi为中心的超球面半径。实验研究表明，Nr的值与搜索算法的性能相关。此外，随着维数D的增加，X的大小和Nr的体积也会增加，从而导致算法性能下降，这被称为维数灾难。

由于连续优化问题中函数的复杂性，大多数现有方法将它们视为黑盒问题并提取特征以表示适应度地形特性。具体来说，许多决策向量是通过在问题的决策空间中进行抽样，并计算其目标值，然后基于这些目标值来计算各种特征。人们认为算法的性能高度依赖于问题的情况[91]，因此这些与情况有关的特征可以在算法性能和问题难度之间架起桥梁。这个想法简单明了且合理，但是它遭受了维数诅咒，由于实际问题仅允许进行少量函数评估，因此对于复杂问题，计算的地形表征很可能不准确。

3.1.3 特征提取方法与算法配置 随着引入的复杂优化算法的数量增加，从给定的算法组合中为待优化问题选择最佳算法已成为巨大的挑战。事实上，没有一个万能的进化算法适用于所有任务，为不同任务选择最佳算法往往需要经历漫长而令人沮丧的练习[92]。基于适应度地形的特征提取方法为此打开了一个新思路。例如，Sallam等[93]设计了一种基于适应度地形的自适应算子选择的DE算法，该算法同时使用了适应度地形信息和种群历史性能的度量，能够从5个算子的集合中选择最佳DE变异策略。此外，他们还提出了一个基于改进的信息地形负向搜索特征的多目标含约束差分进化算法来分析目标函数和约束地形，以便在进化过程中更好地选择算法的最佳进化算子[94]。但是，单个特征只能提供有用地形描述的一部分信息，因此特征的提取与选择在算法配置上的应用具有很大的局限性。

3.2 展望

针对适应度地形分析技术中存在的问题，我们拟从以下5个方面对未来进化计算的发展方向及其在适应度地形分析上的应用进行展望。

3.2.1 基于适应度空间地形的测试函数集优化设计 针对现存基准函数集无法涵盖优化问题基本特性的缺陷，充分利用适应度地形分析技术，进行补充和优化，建立更加完备的基准测试函数集。近年来，带有数据分析功能的墨尔本算法测试实例库已提出了包含多种用于分析和可视化优化问题(或问题集合)的实例空间的技术[95-97]。另外，Tian等[98]也设计了一种树结构来描述多元连续函数，利用树结构随机生成海量函数的技术已取得初步成果。目前，对无约束静态单目标、多目标测试函数集的设计比较成熟，而动态或约束条件下的函数生成还处于发展阶段。因此，通过将复杂环境因素考虑在内，针对测试问题中的高维、多目标、强约束、多模态、动态等特点[99]，分析和验证及改进其合理性，进一步补充设计基准测试问题以及更加科学合理地优化基准测试问题集是一个值得深入研究的方向。

3.2.2 基于适应度地形的高维特征选择方法研究 适应度地形特征选择问题本质上是组合优化问题，随着特征维数的增加会导致“维数灾难”。传统的穷举法容易陷入局部最优，而进化算法作为一种强大的全局搜索技术，已在数百个特征选择问题上显示出了较好的性能。例如，Sherrah等[100]首次将遗传规划算法用于特征选择问题，采用广义线性模型作为分类器来评价所选特征的适应度。Hong等[101]使用一种二进制向量表示每个个体，利用二进制位将预先定义的小数转换为整数来表明对应的特征是否被选择。这些算法都有效降低了高维数据集上搜索空间的维度。另外，对于高维特征，快速最近邻搜索库(fast library for approximate nearest neighbors，FLANN)也可以较好地解决这些问题[102]。它是一个对大数据集和高维特征进行最近邻搜索的算法集合，不但实现了一系列查找算法，还包含了一种自动选取最快算法的机制，通过进化算法的作用实现了特征从高维到低维的有效映射。但是，算法的稳定性不仅与适应度值的差异相关，所选特征的一致性也会产生影响。因此，提出新的稳定性强的搜索算法也是一项重要任务。

3.2.3 基于特征学习的自适应智能优化算法设计 当将进化算法应用于优化问题时，算法选择和参数设置是两个关键问题。如何训练基于适应度地形特征的良好性能算法的选择或模型配置是亟待解决的问题。虽然,目前已有不少研究人员设计了自适应进化算法。例如，郭一楠等[103-104]提出了基于进化算子历史信息的自适应调整选择机制和自适应混合变异文化算法，来同时提高算法解决问题的收敛速度。Sallam等[93]通过在差分进化算法的自适应算子选择机制中同时考虑适应度地形信息和进化算子的历史性能，提出了一种新算法(LSAOS-DE)，以便在进化过程中动态选择最合适的差分进化算子。但是，以上成果都没有从根本上改变进化算法的机理和设计具有本质区别的新算法。另外，生产生活中的实际优化问题，其最优解和适应度地形很难预先获得，如何快速可靠地感知其适应度地形的主要属性特征来指导算法设计，具有重大需求和理论价值。因此，从问题性质和种群数据入手，利用与进化搜索紧密相关的地形特征(比如搜索性、对称性)，建立基于学习的自适应选择机制，使得求解过程中能够根据提取的问题特性来自动调节最佳的搜索算法和策略，并根据问题特征对算法进行在线自适应调整，完成针对实际优化问题特性的优化策略自主选择和优化算法的自动构建，实现更加智能的新一代优化算法是一个极具潜力的发展方向。

3.2.4 基于适应度地形的多目标方法研究 目前，单、多模态优化中对单目标的适应度地形分析的研究很多，但是对多目标的优化还没有引起重视。决策空间存在多个帕累托解集(Pareto set, PS)对应目标空间同一个帕累托前沿(Pareto front, PF)的问题被称为多模态多目标优化问题。在该问题中，多个目标之间经常存在复杂的冲突性，某目标性能的改善可能会引起其他多个目标性能的降低，从而使多目标Pareto最优解集分析的难度随目标个数的增加而激增，因此急需对多目标Pareto最优解集寻求有效的技术手段。针对现有多模态多目标研究的不足，Verel等[105]分析了多目标组合搜索空间的属性和目标函数间的相关性，总结了基于主要适应度地形特征的多目标局部搜索算法设计指南。另外，Kerschke等[106]设计了一个基于特征的用于连续和约束优化问题的R语言包(an R package for feature-based landscape analysis of continuous and constrained optimization problems，FLACCO)。通过这种方式，将来可以在相同条件下进行地形分析以及自动算法选择技术的研究。以上工作构成了适应度地形在多模态多目标优化研究的基础。但是，基于适应度地形的多目标方法研究仍处于发展阶段，而利用决策空间与目标空间的结合可能从中获得新的见解。比如，构建可视化的寻优过程可以辅助算法有效策略的设计及学习过程的开发[107]，检测多目标地形有意义的属性[105]，以及利用适应度地形分析技术设计更高效的多目标进化算法。

3.2.5 适应度地形分析技术在约束问题上的应用 现实中很多优化问题都含有众多的约束条件，使用传统的确定性方法很难求解。近年来，已经提出了许多进化算法来解决约束优化问题，但是在此类设计中尚未充分探索适应度地形信息。适应度地形分析是一项关键技术，这引起了人们对于解空间的极大关注。Malan等[108]提出了一个约束违反地形特征来分析受约束的连续搜索空间的性质。Poursoltan等[109]设计了一种熵特征来量化约束问题适应度地形的崎岖性。但是，并没有对不可行区域的适应度空间地形进行表征。因此，对约束问题可行区域的特征设计和不可行区域难度表征的研究是一个新方向。

4 结语

优化问题包括待优化的目标函数，影响函数数值的变量，以及未知变量的一组约束。尽管优化问题表述起来很简单，但是考虑到现实世界中的诸多因素，优化问题就变得复杂。适应度地形分析技术可以使研究人员避开耗时的反复实验方法来解决优化问题，而将注意力集中在优化问题本身。它不仅为我们提供了有用的指标来指示优化问题是否具有某些特性，还可以使研究人员提前确定哪些类别的优化算法在当前问题上表现更好，甚至可以预知特定算法的哪些参数配置将表现最佳。因此，适应度地形分析技术拥有巨大的发展潜力，并有可能推动人工智能行业在学术界及产业界的进一步发展。另外，优化算法的目的是找到目标函数最大或最小化的未知数的可行解，这对帮助适应度地形分析技术解决优化问题具有天然的优势。

因此，本文对进化计算在适应度地形中的研究做了较为全面的回顾，并对进化计算的主要特点、分类、理论基础和适应度地形的定义、特性、现状这两大方面进行了详述。针对适应度地形分析技术中演化生成问题及实例、特征维数灾难、特征提取方法及算法配置等突出问题，本文从测试函数集优化设计、高维特征选择方法研究、自适应智能优化算法设计、多目标方法研究和适应度地形分析技术在约束问题上的应用这5个方面进行了总结与展望。