深度学习网络用于贝多芬钢琴奏鸣曲创作时期分类的研究

夏一婷，江怡维，李天然，叶 涛

(1.南方科技大学 电子与电气工程系，广东 深圳 518055；2.星海音乐学院 作曲系，广东 广州 510006)

1 介 绍

路德维希·凡·贝多芬(Ludwig van Beethoven，1770—1827)是欧洲古典音乐的著名代表人物之一.作为一名伟大的作曲家，贝多芬的创作题材广泛、个人风格鲜明，其作品对古典音乐的发展有不可磨灭的贡献.其中，1795—1822年间的32首钢琴奏鸣曲的创作几乎贯穿了他的一生，反映了他在不同时期下对社会现实及个人命运的思考.随着社会环境和生活经历的变化，他的音乐创作风格也在发生改变.音乐学界通常按时间将贝多芬钢琴奏鸣曲的创作时期分为早、中、晚3个时期[1].我们利用mLSTM(multiplicative Long Short Term Memory)深度神经网络模型对贝多芬的32首钢琴奏鸣曲进行了学习，并对钢琴奏鸣曲的创作时期进行了自动分类.据我们了解，这是第一个把神经网络用于贝多芬钢琴奏鸣曲的创作时期分类的研究.我们希望通过训练能使神经网络学习到贝多芬不同创作时期的音乐的艺术特征，从而使其有不错的分类表现.在此工作中，我们创建了BPS MIDI数据库(Beethoven Piano Sonata MIDI Dataset)，可用于与贝多芬钢琴奏鸣曲有关的其他研究.

2 相关工作

音乐学界对贝多芬钢琴奏鸣曲分类的方法为按作品的创作时间及对应时期分类[2].贝多芬的创作早期为1792—1802年，创作了钢琴奏鸣曲No.1—15以及No.19、No.20共17首作品.这期间贝多芬的创作受古典主义时期莫扎特、海顿等的影响，作品的结构相对工整，音高方面多利用四五度调性关系进行展开，材料上常在一个乐章中使用多个主题音调.贝多芬的创作中期为1803—1814年，创作了钢琴奏鸣曲No.16—18，No.21—27共10首作品.这一时期贝多芬的写作技法更加娴熟老练，个人风格也更加鲜明，展现出极强的个人英雄主义色彩.具有展开性的长大尾声是这一时期所创作的奏鸣曲的重要结构特点.音高方面多使用三度关系的调性进行循环与展开，旋律主题往往共有同一个音高逻辑.贝多芬的创作晚期为1815—1827年，创作了钢琴奏鸣曲No.28—32共5首作品.与其他晚期作品相同，这一时期，贝多芬创作的钢琴奏鸣曲音乐语言也更加个人化、内省化(具体的分类情况见表1(见 第354页)).在《贝多芬：音乐的哲学》(Beethoven：The Philosophy of Music)一书中，社会学家Adorno[3]认为贝多芬的作品随时代的变化有深刻的哲学意义.郭舒淳[4]阐释了在套曲结构形式、观念驱动下的音乐内涵方面，不同创作时期的贝多芬钢琴奏鸣曲呈现出不同特点.Churgin[5]分析了贝多芬奏鸣曲的主题随不同时期的变化情况，并列出了部分不同时期作品的分类情况.这说明贝多芬钢琴奏鸣曲的特征随创作时期的不同而有所区别，使用神经网络对这些钢琴奏鸣曲按创作时期进行分类是可行的.

表1 贝多芬钢琴奏鸣曲的创作时期分类情况Tab.1 Chronological classification of Beethoven’s piano sonatas

随着深度学习的发展，神经网络在各式各样的音乐分类任务上也能有良好的表现.Choi等[6]把音频的Log-amplitude(振幅对数)和Mel-spectrogram(频率非线性变换后的声谱)作为输入，设计了卷积循环神经网络(Convolutional Recurrent Neural Network,CRNN)分别用于音乐的流派、情绪、乐器、年代分类，该模型的AUC(Area Under Curve)几乎都高于0.7，最好的略高于0.9.Gallardo[7]使用支持向量机(Support Vector Machine,SVM)模型对音乐的各个时期进行分类：巴洛克、古典、浪漫主义、现代音乐等，把音频转换为Humdrum格式或MusicXML格式后，再进行特征提取，不同特征下的分类准确率大都在70%～90%之间.特征提取分类法用于奏鸣曲和回旋曲的曲式分类任务，准确率约为80%[8].神经网络还可用于音乐作品的作者分类，如Micchi[9]使用短时傅里叶变换分析(Short Time Fourier Transform Analysis)在6个作曲家中确定某一作品的归属，准确率可达70%.在音乐分类中最为常见的流派分类问题上，Costa[10]等把音频信号转换为声谱图，从这些时频图像中提取纹理特征，然后在分类系统中用于音乐类型的建模，最终流派分类的准确率可达80%左右.Oramas等[11]分别使用音频文件、评论文字、歌曲封面对同一音乐进行多标签流派分类，结果显示使用文本信息分类的效果最好，使用音频的效果次之.

3 模 型

音乐和语句都是与时间顺序有关的序列，音乐中各个音符的先后顺序、语句中各个字的前后关系都具有一定的意义.由文献[12-13]可知，把自然语言模型运用在音乐样本上也能得到类似的效果.出于以上考虑，我们把音乐样本转化为自然语言序列再进行分类，从而能有效地保留音乐信息.

3.1 数据表示

采用文献[12]中的方法，按时间先后顺序把音乐片段中的信息转化为自然语言序列.这些信息包括：

(1)“n_[音高]”：音高为0到127之间的整数(包含0和127).即音高=1,2,3,…,127.

(2)“d_[时值]_[附点数]”：时值为二全音符(Breve)、全音符(Whole)、二分音符(Half)、四分音符(Quarter)、八分音符(Eighth)、十六分音符(16th)和三十二分音符(32nd).附点数为0，1，2，3.

图1 用我们的数据表示方法编码的示例小节Fig.1 An example bar used to be encoded by our data representation

(3)“v_[力度]”：力度为4到128之间4的倍数.即力度=4,8,12,…,128.

(4)“t_[速度]”：单位bpm(beat per minute).速度为24到160之间4的倍数.即速度=24,28,32,…,160 bpm.

(5)“.”：时间步结束.每个时间步的长度和一个十六分音符的长度相同.

(6)“ ”：音乐片段结束.

例如，图1中的这一小节乐谱(出自Piano Sonata No.9 in E major,Op.14 No.1第二乐章)转化为自然语言序列为：

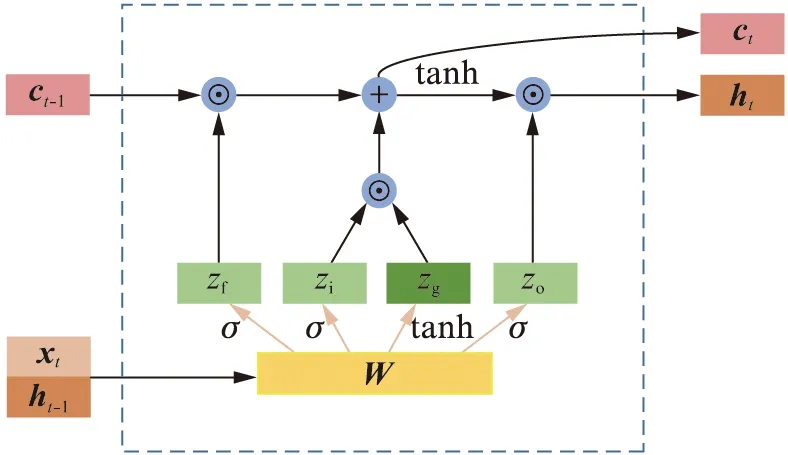
图2 mLSTM单元的结构示意图Fig.2 Structure diagram of mLSTM unit

t_80 v_64 d_quarter_1 n_47 v_64 d_half_1 n_50 v_64 d_half_1 n_54 v_64 d_quarter_1 n_59......v_64 d_eighth_0 n_46 v_64 d_eighth_0 n_58......v_64 d_quarter_0 n_47 v_64 d_quarter_0 n_59......

3.2 mLSTM单元与mLSTM层

mLSTM单元(multiplicative Long Short Term Memory Unit)与LSTM单元结构相似，都能记忆长期和短期的输入数据，对处理与时间顺序有关联的数据十分有效.不同之处在于mLSTM单元的权重矩阵W依赖于每一时刻的输入，对语言进行字符级别的建模时比LSTM单元表现更好[14].一个mLSTM单元的结构示意图如图2所示.

mLSTM单元的运算方式：

m=Wmxxt⊙Wmhht-1，

(1)

W=Wxxt+Whm，

(2)

(3)

ct=zf⊙ct-1+zi⊙zg，

(4)

ht=zo⊙tanh(ct).

(5)

其中：xt，ht-1，ct-1分别为当前时刻的输入数据、上一时刻的mLSTM单元隐状态(Hidden state)和细胞状态(Cell state)，三者输入当前时刻的LSTM单元；Wmx和Wmh分别为在逐元素乘法步骤中，当前输入xt的权重矩阵和上一时刻隐状态ht-1的权重矩阵；m是为了书写美观而引入的变量；W为权重矩阵；Wx和Wh分别为计算W所需的关于当前输入xt的权重矩阵和关于m的权重矩阵；zf，zi，zo，zg分别为遗忘门(Forget gate)、输入门(Input gate)、输出门(Output gate)和门之门(Gate gate)，这4个门控制了当前mLSTM单元对输入数据的遗忘程度、处理程度和输出程度；公式中和图中⊙均表示矩阵的逐元素乘法；σ为sigmoid函数.经过运算，得到的ht和ct分别为当前时刻的mLSTM单元的隐状态和细胞状态.通过更新每一时刻的隐状态和细胞状态，mLSTM单元可学得数据的时间变化规律.

许多个mLSTM单元按时间步骤排列形成一个mLSTM层(mLSTM layer).一个mLSTM层中的mLSTM单元数也称为该mLSTM层中神经元的个数.

3.3 音乐特征提取模型(mLSTM模型)

音乐特征提取模型由一个编码层和一个mLSTM层构成，其结构如图3所示，其中：xt-1为上一时刻输入，x′t为所预测的当前时刻输出.

使用3.1节中的方法处理音乐样本，得到其对应的自然语言序列.取该序列某时刻的值输入mLSTM模型，预测下一时刻的值.mLSTM模型的Embedding层神经元个数为64，mLSTM层神经元个数为4 096，其目标函数为下一时刻的预测值与真实值的交叉熵损失(Cross entropy loss).反向传播时更新两个层的权重，让预测值尽可能接近真实值.因为自然语言序列由音乐片段转化而来，可认为训练好的mLSTM模型可以根据当前时刻的音乐信息，较为准确地预测下一时刻的音乐信息.

3.4 分类模型

分类模型由3.3节中已训练好的mLSTM模型和softmax回归层构成，结构如图4所示，其中：x为奏鸣曲对应的自然语言序列；y为所预测的创作时期类别.

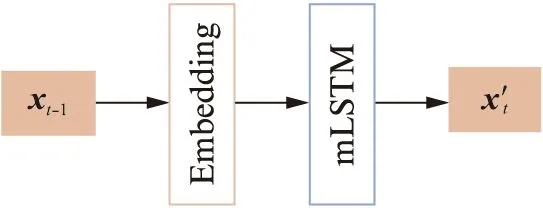
图3 音乐特征提取模型的结构Fig.3 Structure of music feature extraction model

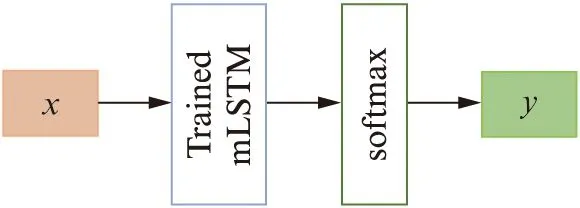
图4 分类模型的结构Fig.4 Structure of classification model

同样使用3.1节中的方法处理贝多芬钢琴奏鸣曲音乐样本，得到对应的自然语言序列.把序列输入训练好的mLSTM模型，取最终的隐状态(一个4 096维的向量)作为包含音乐样本信息的向量样本.softmax回归使用极大似然估计法，最大化每个样本被正确分类的概率.softmax回归把输入数据xi归为类别j的概率为

(6)

其中：yi为类别标签；θ为softmax的参数；k为类别个数.使用带L2正则化的softmax回归对这些向量进行分类，预测该音乐样本所属的时期.损失函数为

(7)

其中：m为样本个数；n为每个样本的维度个数；λ为正则化参数；1{·}为示性函数，当括号内命题为真时函数值为1，反之为0.

4 BPS MIDI数据库

我们建立了一套贝多芬钢琴奏鸣曲的BPS MIDI数据库作为本研究的训练以及测试样本库.我们从网上搜集了全套贝多芬钢琴奏鸣曲的音乐资料，一共包含103个MIDI文件，每个文件的时长从1到13 min不等.其中早期、中期、晚期(按奏鸣曲的创作时期分)分别包含58，29，16个MIDI文件.每个乐章均取前1 min的片段作为样本，并按每个乐章的不同时长，每3 min截取后1 min的片段作为样本，由此一共得到早期样本132个，中期样本67个，晚期样本43个，即一共242个不同时期时长均为1 min的音乐样本.由此构成了我们的BPS MIDI数据库.

5 模型训练与评估

5.1 训练音乐特征提取模型(mLSTM模型)

采用文献[12]中的方法，混合Video Game MIDI数据库与BPS MIDI数据库中的音乐片段作为样本训练mLSTM模型.Video Game MIDI数据库中含823个游戏背景音乐的MIDI文件，时长从26 s到3 min不等.为了使训练样本多样化，对这些音乐片段进行一系列变换，包括时间变换(加速、减速)，音高变换(每个音都升高或降低一个大三度).然后采用3.1节中的方法对样本进行编码，得到对应的自然语言序列.把这些序列拼接在一起，按9∶1的比例随机分为训练集和测试集.再把训练集平均分为3个子集以便后续处理.每个训练子集中大约包括18 600个音乐样本，测试集中大约包括5 800个样本.

依次使用3个训练子集对mLSTM模型进行训练并在测试集上测试.在每次训练前ht和ct均初始化为0.训练3轮，采用Adam方法进行优化，得到在测试集上的平均交叉熵损失为0.65.

5.2 训练分类器

表2 10折交叉验证结果Tab.2 Results for 10-fold cross validation

经过上一步训练的mLSTM模型可当做一种特殊的编码器.为了使样本有较好的训练效果，对BPS MIDI数据库中各时期的典型作品[15](即早期作品No.1—6，中期作品No.21、No.26，晚期作品No.28—32)的样本进行时间变换(加快、减慢)和音高变换(所有音上移、下移大三度)，得到早期样本244个，中期样本231个，晚期样本387个，全部样本共862个.为了使各时期样本数量平衡，在晚期样本中随机取240个，最终一共得到715个音乐样本.把这些音乐样本输入mLSTM模型，取模型中mLSTM层的最终隐状态(4 096维的向量)作为编码结果，使用softmax回归进行分类.使用10折交叉验证(10-fold cross validation)评估模型的效果，结果如表2所示.

最高准确率所对应的测试集混淆矩阵(Confusion matrix)及分类报告(Classification report)如表3，表4所示.

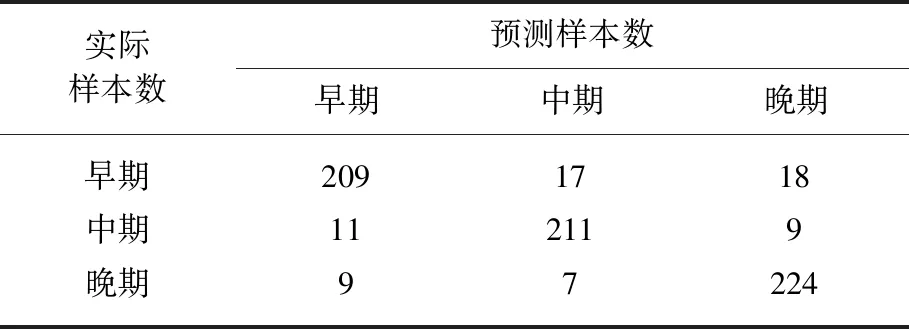
表3 所有测试样本的混淆矩阵Tab.3 Confusion matrix of all test samples

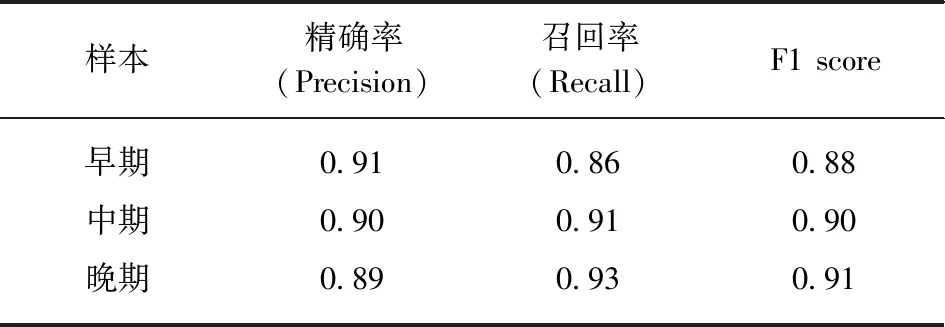
表4 所有测试样本的分类报告Tab.4 Classification report of all test samples

由表3和表4可知，mLSTM模型+softmax回归的平均准确率为90.06%，最低约为80%，最高可达97%.精确率、召回率和F1 score在0.90左右.说明mLSTM是一种有效的特征提取器，可通过一个4 096维的向量囊括一个音乐样本的大致信息.mLSTM模型+softmax回归在贝多芬钢琴奏鸣曲创作时期分类任务上有出色的表现.

5.3 模型评估

mLSTM模型+softmax回归有以下几个优点：(1)使用外部数据库进行训练数据扩充，解决了原训练数据数量较少的问题，同时也能得到理想的分类效果；(2)mLSTM模型能有效提取符号音乐的特征，所提取的特征向量能够有效地被机器学习算法分辨；(3)由于mLSTM模型的本来目的是用于提高预测序列中后一时刻字符的准确程度，故还可用于完成音乐生成的任务.

6 结 语

mLSTM模型+softmax回归在对贝多芬钢琴奏鸣曲创作时期分类这一任务上有出色的表现，准确率大都在90%左右，最高可达97%.精确率、召回率和F1 score在0.90左右.通过把符号音乐转化为自然语言序列进行处理，避免了主观特征提取的困难.整个训练过程中使用外部数据进行训练数据扩充，解决了原数据量较少的问题.我们认为这一模型在其他任务上也能有不错的表现，如对多个作曲家创作时期的分类、控制mLSTM模型进行音乐生成等，这些课题有待进一步研究和探索.