一种新型的特征平滑处理的民乐音符起始点检测算法
2021-09-23马连航阮林萍汪万涛
马连航,王 军,阮林萍,汪万涛,文 亮,杨 帆,赵 罡
(1.中电海康集团有限公司,浙江 杭州 311100;2.北京调皮猴科技有限公司,北京 101102)
1 研究背景
音符起始点是音乐特征信息中最基础的特征,其检测任务是基于内容的音乐信息检索(Music Information Retrieval,MIR)领域的关键环节和基础性课题,也是高级音乐分析任务(如基频估计、节奏分析、节拍跟踪等)的前提[1-2].换言之,音符起始点检测的准确度和精度极大程度地决定了后续高级特征检测和处理的准确度上限.目前较为成熟的音符起始点检测算法大多借鉴了语音端点检测方法[3],并在此基础上加以改进,得到适用于音乐信号的检测方法.
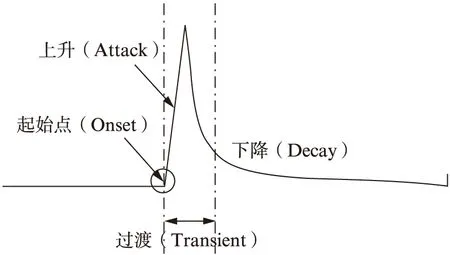
图1 一个音符的时域信息描述:起始点、上升、过渡和衰减[2]Fig.1 Temporal description of a note:onset,attack,transient and decay
从信号处理的角度来看,音符起始点(Onset)是指音乐中某一音符开始的时间,其起始阶段能量突然上升(Attack),经过一段过渡期(Transient)后能量逐渐衰减(Decay),如图1所示[2].传统的音符起始点检测算法直接或间接地以信号谱分析为基础进行设计,需要通过如短时傅里叶变换(Short-Time Fourier Transform,STFT)、常数Q变换(Constant Q Transform,CQT)[4]和小波变换(Wavelet Transform,WT)[5]等信号变换方法实现音频信号从时域到频域的转变;Bello等[6]利用信号变换输出的时谱图,提取幅度谱和相位谱作为声学特征;Böck等[7-8]为了得到更符合人耳听觉特性的声学特征,使用Mel变换及滤波后的能量谱作为声学特征,并有效地提高了检测精度.为了加强算法对音乐信号非平稳部分的自适应能力,Shao等[9]提出了基于匹配追踪的稀疏分解算法,该算法在MIREX 2013数据集上表现效果良好.
近年来,随着机器学习在语音识别方向的应用和普及,神经网络相关算法也被用于音符起始点的检测任务中,通过网络自主学习音乐信号与音符起始点的关系[10-11].实际上,在MIREX大赛上,以神经网络模型为基础的检测算法已经多次蝉联音符起始点检测任务的冠军.Marolt等[12]在2002年就提出,通过结合神经网络和多个听觉滤波器组,可以实现钢琴的起始点检测任务;Huh[13]将概率模型和卷积神经网络(Convolutional Neural Networks,CNN)结合,对Böck数据集进行起始点检测.Stasiak等[14-15]使用自相关函数及卷积神经网络作为音频起始点算法的提取模型;Eyben等[16]利用训练好的循环神经网络对MIREX数据集进行起始点检测,获得同一集合上的最优F1值.该模型经过后续多次迭代和修改,已成为可靠性较高的起始点检测算法之一[17-18].
值得注意的是,尽管目前的音符起始点检测算法日益成熟,在各自的数据集上都能呈现出较高的F1值,但当前国内外关于音乐音符起始点检测的研究大多数以西洋乐为研究对象,针对中国民乐的研究少之又少,主要原因是缺少高质量的带标注的数据集.事实上,民乐的起始点检测更为复杂.究其原因,一方面在于民乐中存在大量时值较短的音符(如十六分音符),其衔接紧密,容易产生能量耦合;另一方面在于民乐强调形散神不散,因此民乐乐器(如古筝、古琴[19]等)通常利用复杂的技法和指法(如摁、滑、揉、颤等)使声音和频率产生波动来呈现情感的表达,但繁杂的技法会影响甚至改变音符的起始点特征,其中又以弦乐类乐器尤为明显.所以现有的西洋乐器起始点检测算法难以直接运用至民乐的起始点检测任务上,其挑战在于设计和构造适用于民乐的检测算法以及提取和凸显民乐的声学检测特征.
针对上述问题,本文选取了中国传统民族乐器的代表——古筝作为研究对象,采集了古筝的部分考级曲目的音频,并在专家的指导下对音符起始点进行标注,率先构建了一个带有详细标签、包含3 529条记录的古筝音符起始点数据集(曲目目前还在不断扩充中),并在此基础上搭建了深度卷积神经网络模型.此外,由于传统的神经网络特征预处理方法无法凸显古筝音符的起始点特征,本文提出了一种新型的特征平滑处理方法——基于极值筛选的包络平滑(Extremum fiLtering based Envelope Smoothing,ELES)方法,首先采用极值筛选的包络平滑方法对训练数据的均值和标准差进行平滑处理,再经过标准化方法强化起始点特征,随后送入网络模型进行训练.结果显示采用ELES标准化后的特征数据能更加凸显音符起始点的能量变化特性,更有利于提高模型的分类准确性.最后通过实验验证了本文方法相比于传统音频信号处理方法在准确度上的优越性,以及对于特殊的古筝技法和连续十六分音符起始点检测的有效性.
2 新型的特征平滑处理的民乐音符起始点检测算法
本节将介绍一种基于新型的特征平滑处理的民乐音符起始点检测算法,首先描述算法的总体流程,然后重点阐述音频的特征选取和标准化处理方法,最后介绍用于音符起始点检测的深度卷积网络模型.
2.1 算法概述
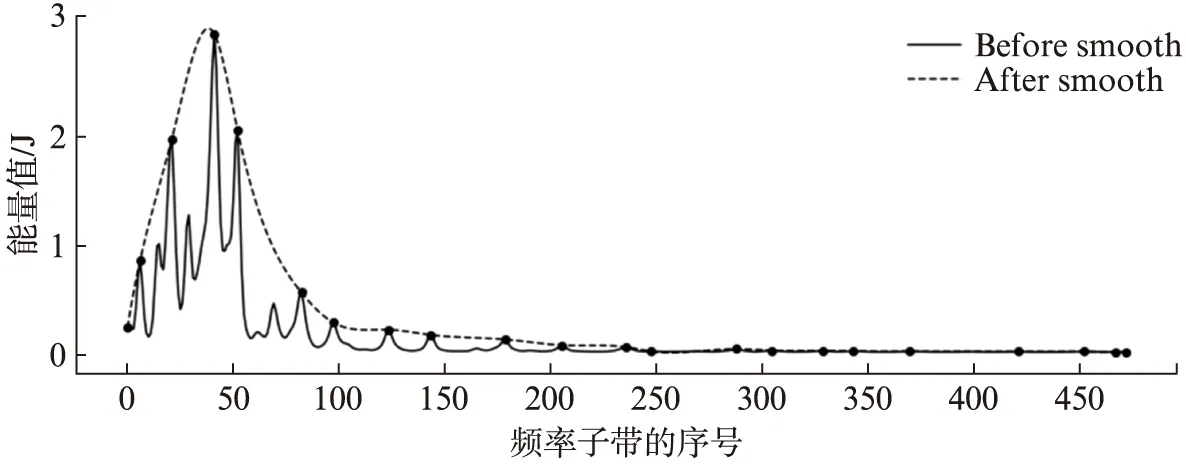
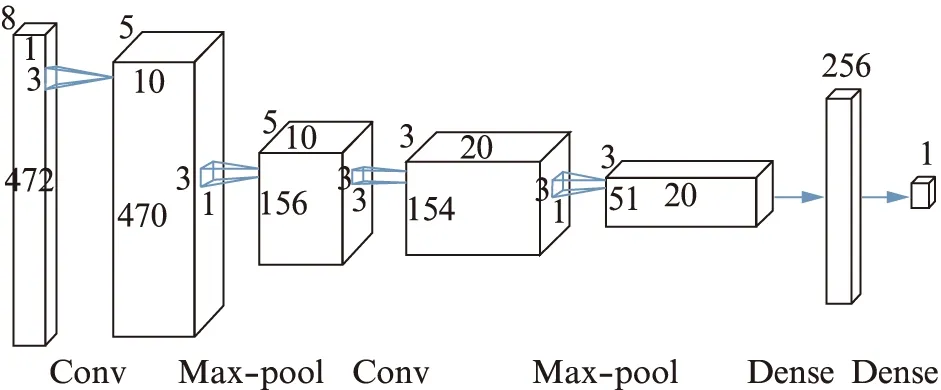
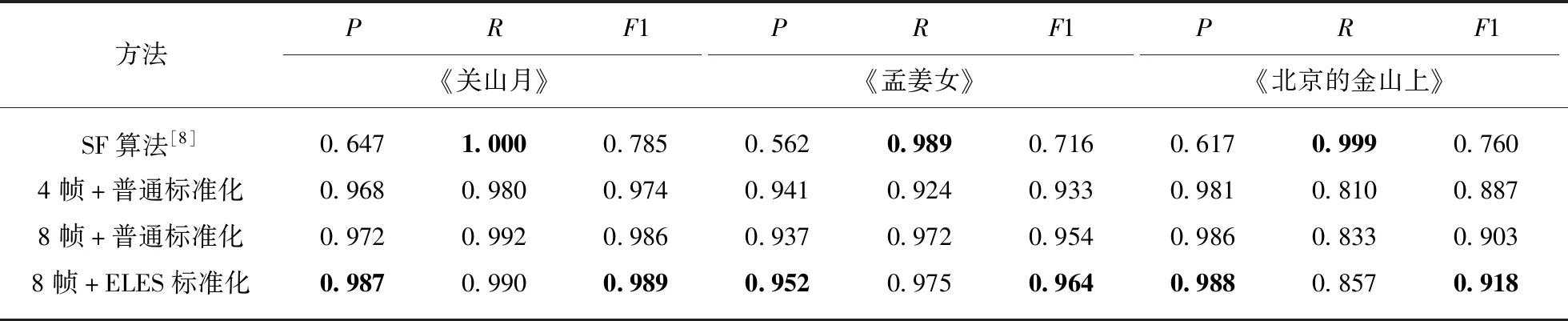
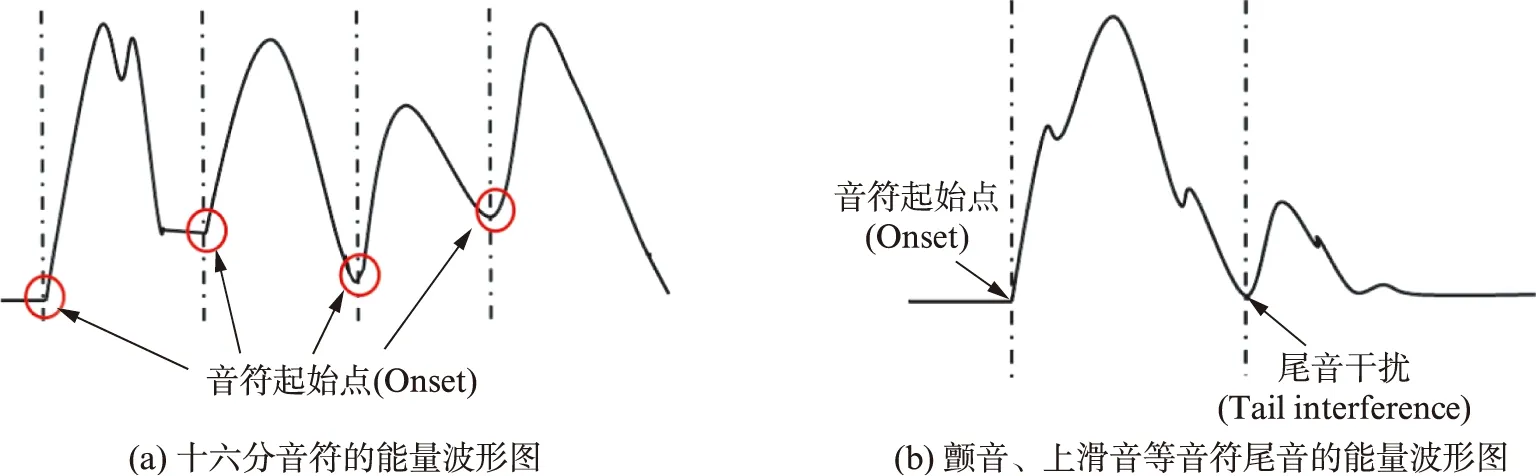
本方法将音符起始点检测任务建模为一个有监督的二分类问题,算法流程如图2所示.首先,给定一段原始音频(wav格式),将其进行时频变换后得到长度为N的音频时谱图(Spectrogram)X={x1,x2,…,xN}∈N×D.然后,对时谱图中的每一帧xt(t=1,2,…,N)着重进行特征选取并采用ELES方法进行标准化.最后将特征数据(x′t,yt)送入神经网络,其中x′t∈D′(D′ 图2 音符起始点检测算法流程图Fig.2 Flow chart of note onset detection algorithm 设计一个合适的音频特征表达方式是众多音频信息检索任务(如翻唱识别、主旋律抽取、音乐流派分类等)最具挑战性的工作,将合适的特征送入分类器中往往会得到更好的分类效果.在音频信号分析过程中,通常将一段音频信号的1维时域表示变换为2维的时域-频域表示,即时谱图.常用的转换方式有STFT、CQT、WT等.本文采用的STFT,因为其更能反应信号低层次的特征信息.STFT后的时谱图记为X={x1,x2,…,xN}∈N×D,每帧的特征数据为xt∈D,t=1,2,…,N. 民乐乐器(如古筝、琵琶等)的大多数音符具有和西洋乐器(如钢琴、吉他、贝斯等)相似的特性,其在起始阶段会出现能量激增的过程.因此对于一个属于音符起始点的帧xt(下文简称为起始帧)来说,起始帧之前的p帧,即xt-p,xt-p+1,…,xt-1,每一帧的能量是极其微弱的,而在其之后的q帧,能量则会呈现突然升高的趋势.为此,在构建起始点检测任务的神经网络模型时,输入除了应包含当前帧xt,还应当包括其上下文帧的特征数据.本文选取的特征数据为当前帧xt及其上下文共8帧(p=4,q=3)的数据,即xt-4,xt-3,xt-2,xt-1,xt,xt+1,xt+2,xt+3. 深度神经网络的初始输入数据通常都需要经过标准化(Standardization)处理.其目的是使每个维度的特征数据取值都在相同的范围内,从而使得网络模型在训练过程中更加容易收敛.常用的标准化方法如下: (1) 其中:xi代表第i个样本(1≤i≤N);μ和σ分别代表样本的均值和标准差.标准化后,样本每个维度都满足均值为0、方差为1的高斯分布. 本文首先按照上述传统的标准化方法对训练数据进行预处理,处理后的起始帧及其上下文帧共8帧的频谱图如图3(a)所示.可以看出频谱能量随时间变化的规律并不凸显起始点的特性,且图中存在较多毛刺和凸起,不利于神经网络的分类.为此,我们提出了ELES方法,对训练数据的均值μ和标准差σ进行平滑化,然后采用平滑后的均值与标准差进行输入数据的标准化处理.经过ELES标准化后的起始帧及其上下文帧共8帧的频谱图如图3(b)所示,可以发现图中的频谱能量较为集中,过滤了大多数的毛刺与凸起,且前4帧能量较低,后4帧能量则逐渐升高,符合音符起始点的能量变化规律. 图3 采用传统标准化方法(a)和经过ELES方法标准化(b)后的频谱图对比Fig.3 Comparison of spectrogram by using traditional standardization (a)and ELES standardization methods (b)横坐标表示时间上连续的8帧,包括起始帧(图中两条虚线之间)和其上下文帧(前4帧和后3帧),纵坐标表示能量值. 图4 训练数据的均值μ采用ELES方法平滑前后的变化图Fig.4 The chart of the mean μ before and after adopting ELES approach on training data 图4(见 第318页)展示了训练数据的均值μ在采用ELES方法前后的变化,如图所示,均值μ沿着能量的包络进行平滑,过滤了多数小的毛刺与凸起.ELES方法的伪代码如下所示: 输入:特征数据的均值矢量μ={μ1,μ2,…,μD}∈D. 输出:平滑后的均值矢量μ′∈D. 1:遍历矢量μ中的每一个点,找出其中的极大值点子序列μmax.极大值点定义为该点是序列中前后共m个点中的最大值点; 2:遍历序列μmax中的每一个点,找到其中的极小值点,并将其从序列中删除.极小值点定义为该值是序列前后共n个点中的最小值. 3:重复2的过程,直到极大值序列μmax中找不到极小值点. 4:采用插值拟合方法,用一条平滑曲线拟合最终的极大值序列μmax中的所有点. 5:输出拟合后的曲线即为平滑后的均值矢量. 算法首先从均值向量μ∈D的序列中找到能量极高点序列μmax(第1行,参数选取为m=5),然后不断迭代删除极高点序列μmax中的能量极小值(第2行,参数选取为n=3).最后通过插值拟合,用一条平滑曲线将μmax中的点连接起来(第4行),该曲线即为平滑后的最终均值矢量μ′(第5行).标准差σ的平滑过程与均值μ相同.最后训练数据时,每一帧特征数据都使用平滑后的均值μ′与标准差σ′,采用式(1)进行标准化. 图5 本文卷积神经网络架构图Fig.5 Architecture of our convolutional neural network 本文所采用的CNN架构借鉴了文献[18]的思路,由2个卷积层、2个池化层和2个全连接层组成,如图5所示.采用CNN的原因是对于整首曲子而言,音符的起始点实际是一个时序上的局部特征,起始帧的能量与上下文帧有密切关系,且起始帧在一首曲子中的多个时间点上发生,因此采用卷积的思想可以很好地捕捉到这种时序上的局部特征,同时减少网络的参数量.为避免低频噪声干扰,过滤了STFT后512个频率子带中的前40个子带,因此网络的输入是2维的时谱图(8帧×472个频率子带,频率覆盖范围约为200~2 800 Hz),通过大小为4×3的卷积核后得到10个5×470大小的特征映射图,再通过窗口大小为1×3的最大池化层后,将每个特征映射图的维度缩减为5×156.第2个卷积层的卷积核大小为3×3,最大池化层窗口大小为1×3,得到20个大小为3×51的特征映射图.最后将其送入包含256个神经元的全连接层,输出层只有一个神经元,以sigmoid函数的输出判断是否为音符起始点. 为了验证基于CNN的音符起始点检测算法的准确性,本节将本文所提算法与基于音频信号处理的音符起始点检测算法进行比较.同时,为了验证基于ELES标准化方法的可靠性,将其与采用不同帧数(4帧上下文)和不同标准化(传统标准化方法)的特征预处理方法进行对比.最后进行了本文算法对于连续的十六分音符以及古筝的特殊技法音符的准确性测试. 实验所釆用的古筝演奏音频的原始数据均釆集于无噪音环境中,共包含10首一至二级的古筝考级曲目.原始音频经过STFT后得到时频特征表达,STFT使用的参数如下:音频釆样率(Sampling rate)=44 100 Hz,窗函数釆用汉宁(Hanning)窗,窗函数大小(window_length)=8 192(约为186 ms),步长(hopsize)=1 024(约为23 ms).经过专家指导后进行人工标注,共得到1 777个音符起始点和1 752个非起始点的数据. 训练卷积神经网络的过程中,使用其中的7首曲目当做训练集(包括1 267个起始点和1 242个非起始点),3首当作测试集(《关山月》包含98个起始点和98个非起始点,《孟姜女》包含193个起始点和193个非起始点,《北京的金山上》包含219个起始点和219个非起始点).网络模型的初始学习率为0.05,每5轮验证损失不下降则学习率除以5,优化方法为动量梯度下降法,初始动量为0.9,批次(Batch)大小为1 024,釆用Early stopping策略和5折交叉验证方法,损失函数为二分类交叉熵损失. 本节首先比较了不同帧数的上下文特征数据以及不同标准化方法的算法性能,其中8帧的上下文特征数据包括需分类的当前帧及其前4帧和后3帧,4帧的上下文特征数据包括需分类的当前帧及其前2帧和后1帧,在3首测试曲目上的结果如表1所示.可以看岀釆用8帧上下文加上ELES标准化方法后的特征数据在测试集的3首曲子中都获得了最高的F1值.原因有二:其一,4帧的上下文数据的时间维度太短,包含的特征信息量可能不够,而8帧上下文的特征数据更能准确地反应音符起始点在时间上的特性;其二,经过ELES方法平滑后的标准化过程能够过滤掉大量能量上较小的毛刺和凸起,使得音符起始点的特征更加明显. 表1 本文方法与基于音频信号处理的方法的对比实验结果Tab.1 Performance comparision between our approach and the methods based on audio signal processing 随后,将本文方法与基于音频信号处理的音符起始点检测算法SF(Spectral Flux)[8]进行了对比,结果见表1.从表1中可以看岀,本文方法的F1值远远高于传统的SF算法的.原因是音符的起始点是一个时序上的局部特征,而CNN的卷积层擅长处理的正是局部特性,通过不断训练优化,模型具有准确抓取局部特征的强大能力,在计算机视觉领域的成功应用也验证了这一特性. 为了验证本文方法在检测连续十六分音符和带有古筝技法的音符起始点的有效性,本节选取连续十六分音符段落(包含125个起始点)、大撮(41个起始点)、颤音或揉音(51个起始点)、上滑音(25个起始点)等技法音符起始点,以及部分技法音符尾音中带有能量包络的非起始点(156个非起始点)进行测试.评价指标为准确率(Accuracy)λA,定义为: 检测连续十六分音符的难点在于其每个音符的持续时间较短,且两个音符连接紧密.前一个十六分音符的能量很可能会影响到后一个十六分音符的能量,导致后一个十六分音符的起始点特性不明显(如图6(a)(见 第320页)所示).颤音、上滑音等技法的音符尾音中常包含小的能量波形包络,其能量变化规律与起始点十分类似(如图6(b)(见 第320页)所示),易被误分类为起始点. 实验结果如表2所示,可见本文方法对连续十六分音符以及特殊技法的音符起始点检测的准确率都高于96%,特别是对于大撮技法检测的准确率能达到100%,对易被误分类的非起始点的检测准确率也达到了96%以上. 图6 (a)十六分音符的起始点波形图和(b)尾音中包含低能量波形包络,易被误分类的非起始点Fig.6 (a)Waveforms of onsets of continuous semiquaver notes and (b)non-onsets of the notes having small energy envelopes in the tail 表2 连续的十六分音符和带有特殊技法的音符起始点和尾音上非起始点检测的准确性Tab.2 Accuracy of our approach on continuous semiquaver notes and notes with special playing techniques,as well as non-onsets of ending notes 针对缺乏高质量的带标注的民乐数据集问题,本文于国内率先构建了一个带标签的包含3 529条记录的古筝音符起始点数据集.同时提岀了一种新型特征平滑处理方法ELES,解决了传统标准化预处理过程无法凸显音符起始点声学特征的问题.实验验证了本文方法相比于传统音频信号处理方法在检测准确度上的优越性,以及对于特殊的古筝技法和连续十六分音符起始点检测的有效性.后续我们将持续采集古筝演奏音频并加以标注,同时不断改进特征选取和标准化处理过程.
2.2 特征选取
2.3 特征预处理

2.4 卷积神经网络架构
3 实 验
3.1 实验设置
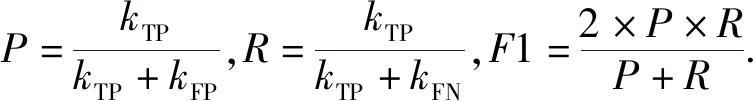
3.2 准确性比较实验
3.3 连续十六分音符和特殊演奏技法实验

4 结 语
