资本利用率、全要素生产率与货币政策

苏 剑,纪 尧

(北京大学 经济学院,北京 100871)

一、问题的提出

技术是经济增长的源泉,技术进步与经济增长高度相关,全要素生产率(Total Factor Productivity,TFP)增长应存在顺周期性。然而,代表性研究[1-5]所测算的中国全要素生产率存在显著的过度顺周期性,本文以Feenstra等[1]的测算结果为例说明该现象,如图1所示。

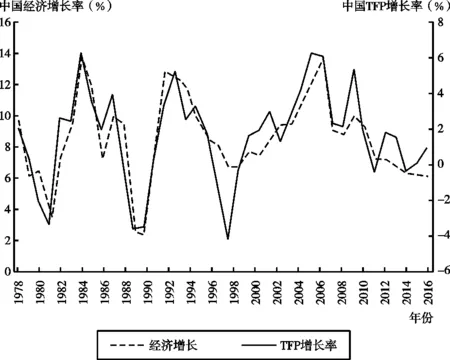
图1 中国经济增长与TFP增长率

已有文献对中国TFP测算结果的不合理之处在于:中国TFP增长率与经济增长率相关性极高,但该现象只有当经济处于平衡增长路径上才会出现。根据已有研究,中国TFP增长率与经济增长的高度相关性在1978—2000年表现得尤为显著,但在该时期,中国经济显然未达到平衡增长。这意味着已有文献关于中国TFP顺周期性的结果存在过度夸大。

产生这一结果的原因是,已有研究存在遗漏投入要素的问题,即遗漏资本要素利用率变量。生产函数中资本服务要素的投入是由资本存量和资本利用率共同构成的。在实际研究中,由于资本利用率的数据不包含在国民经济统计调查体系中,因而,长期以来,相关研究在遗漏资本利用率情况下测算的全要素生产率实际包含高度顺周期的资本利用率,从而导致TFP测算结果的过度顺周期性。

为了说明本文观点,本文首先在控制资本利用率的条件下测算TFP,通过实证说明在测算TFP的过程中遗漏资本利用率将导致TFP的高度顺周期性,而在控制资本利用率后,中国TFP的过度顺周期现象得到改善。与此同时,本文发现未控制资本利用率的中国TFP测算结果高估了中国在1978—2000年的技术进步率,低估了中国自加入WTO以来的技术进步率。控制资本利用率的中国TFP测算结果显示,改革开放在初期对中国技术进步的提升作用远远小于其对资本利用率的作用,并且2000年后中国贸易自由化和投资自由化极大提升了中国的技术进步率。

接着,本文构建了一个带有内生增长特征的水平化创新DSGE模型,从模型脉冲响应角度以货币政策冲击这一典型冲击为例,分析资本利用率在TFP变化中的作用。本文通过模型的脉冲响应函数证实了以下观点:传统忽略资本要素利用率的全要素生产率测算结果会导致全要素生产率的过度顺周期性,并且中国金融市场的不完备性进一步扩大了中国全要素生产率顺周期性。因而,如果在测算生产率时遗漏了相关的投入要素利用率,那么即使生产率本身没有发生变化,生产率的测算结果也可能呈现出顺周期性。

最后,作为延伸,本文进一步探讨了货币政策冲击对TFP的效应,结果显示,货币政策冲击对TFP的影响较小,货币冲击后,TFP迅速收敛至0。已有货币政策的相关研究主要关注货币增速与经济增长的关系[6-8],而本文将视角进一步拓展至货币政策与技术进步,为中国货币政策的研究和执行提供新支持。

二、全要素生产率的测算

资本存量和资本利用率共同构成的资本服务决定了生产函数中的资本服务要素投入。而在现实中,由于资本利用率的数据不包含在国民经济统计调查体系中,长期以来,相关文献在遗漏资本利用率情况下测算的全要素生产率实际包含了高度顺周期的资本利用率一项。因而为了更准确地衡量中国的技术进步率,应在控制资本利用率的情况下,测算中国全要素生产率。本文测算时使用的数据包括Feenstra等[1]测算的不变价下的中国实际GDP、劳动参与人数和平均年度劳动时间。

为了得到中国资本服务变量,本文首先参考杨光[2]的方法得到中国1978—2017年的资本利用率,如图2所示。改革开放提高了中国的资本利用率,从1978年开始,中国的资本利用率经历了一个上升的过程,直到2000年后,资本利用率逐渐下降到1以下,这与中国长期依靠投资拉动经济增长,形成大量的过剩产能有关。

图2 1978—2017年中国资本利用率的测算结果

lnYt/Lt=lnTFP+αlnKt/Lt+εt

OLS回归结果如下:

lnYt/Lt=-0.47+0.74lnKt/Lt

(27.82,0) Adj.R2=0.95

(94.15,0) Adj.R2=0.99

回归结果在1%的显著性水平下显著,在控制资本利用率后,调整后的R2值更高。并且回归结果显示,在控制资本利用率后,中国的资本服务要素产出份额高于普遍认识,达到0.88,这是中国长期依赖投资拉动经济增长的结果。在估计出资本要素和劳动产出弹性后,本文使用国民经济核算恒等式计算得到全要素生产率增长情况(见图3)。测算结果显示,在控制资本利用率后,中国TFP的过度顺周期现象得到改善。

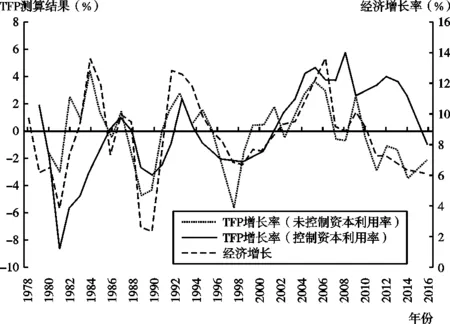
图3 控制资本利用率前后的全要素生产率增长率

通过梳理本文的中国TFP测算结果可以发现,在未控制资本利用率的情况下,1978年以来的全要素生产率呈现下降趋势,而在控制了资本利用率后,1978年以来的全要素生产率呈现上升趋势,这与已有研究结论正好相反。总体来看,1978—2017年间,未控制资本利用率的TFP平均增速为-0.19%,控制资本利用率后的TFP平均增速为0.05%,并且呈现明显的上升趋势。

未控制资本利用率的TFP测算结果严重错估了中国在各个阶段的技术进步率。分阶段来看,1978—1990年的改革开放初期,未控制资本利用率测算的TFP累计毛增长率达到105%,而控制资本利用率后测算的此阶段TFP累计毛增长仅为78%。结合图2资本利用率在改革开放初期迅速上升至1以上的事实,说明由于当时中国处于短缺经济,中国在改革开放初期主要提高了资本利用率,而非技术进步;1990—2000年中国的资本利用率仍然保持在1以上,两个测度结果下的TFP累计增长分别为96%和88%;自2000年中国开启贸易自由化进程后到2010年,两种测度下的TFP累计毛增长分别为114%(未控制资本利用率)和129%(控制资本利用率),表明贸易自由化和投资自由化极大提升了中国的技术进步,并且该效应具有持续性;2010—2017年间两种测度下的TFP累计毛增长分别为88%(未控制资本利用率)和120%(控制资本利用率)。比较两种测度结果,2010—2017年中国的TFP增速实际高于而非低于前期。结合图2显示的中国同期出现的产能过剩、资本利用率大幅下降的问题,测算结果说明已有研究可能低估了加入WTO对中国技术进步的影响,错将资本要素闲置计入技术,从而得出2010—2017间中国TFP增长率低于前期的结论。

根据控制资本利用率后测算的TFP增长率,可以把1978年后中国的TFP发展分为三个周期:1978—1990年作为改革开放第一阶段,1990—2000年作为改革开放第二阶段,2000—2017年作为贸易和投资自由化阶段。由图4可以看出,中国TFP增速在三个阶段呈现递增的状态。2010年后,尽管中国TFP增速仍处在较高水平,但是可以预想到未来将出现下降趋势。一方面,这是由中国研发投入高速增长引起的研发拥挤效应所致。根据世界银行的数据,中国的研发投入强度(研发支出占GDP比例)由2000年的0.89%迅速上升至2018年的2.19%水平,短期内超过了2017年欧盟2.13%的平均研发强度水平,研发投入总量自2016年以来更是连续保持两位数增长。而中国一些地区已经出现了研发投入强度过高的现象,如北京、上海的研发投入强度分别达到了6.17%和4.16%,均已达到世界最高水平。短期内研发投入的高速增长势必会降低研发效率,以至于拉低TFP增速;另一方面,根据前文的测算,中国TFP增长的一个重要推动因素是贸易和投资自由化,因而目前世界范围内兴起的逆全球化进程也将在未来对中国TFP增长造成不利影响。

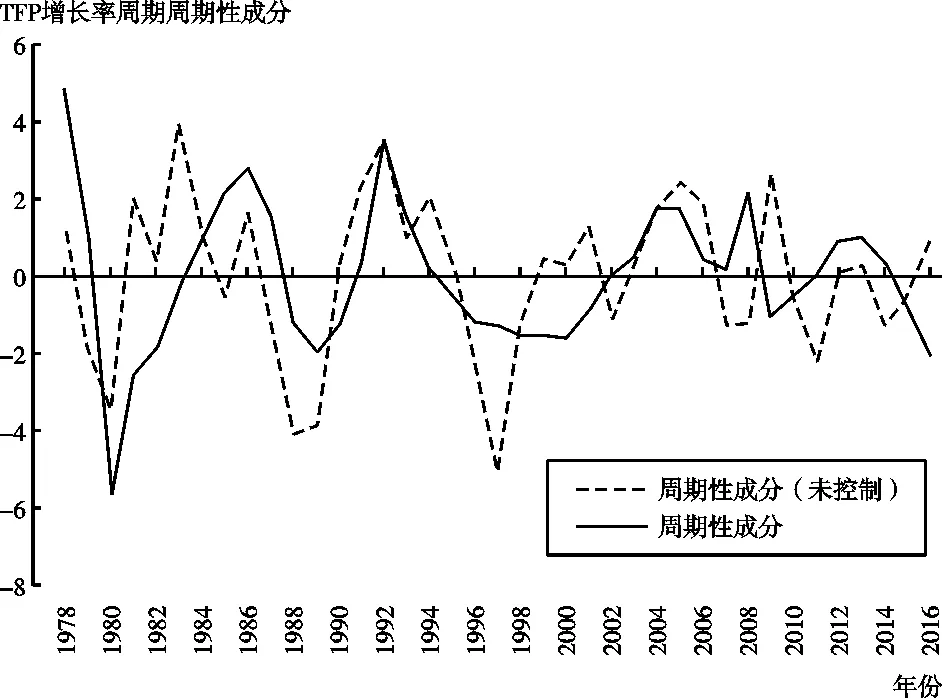
图4 控制资本利用率前后的全要素生产率增长率周期性成分

同时还可以看到,在控制资本利用率后,中国的全要素生产率波动性减小,过度顺周期现象得到改善。使用HP滤波对本文测算的TFP增长率进行去势处理,TFP增长率周期性成分的标准差在控制资本利用率前后分别为2.1和1.7。可见,控制资本利用率显著降低了TFP测算结果的过度顺周期性,TFP增长率的周期性成分波动性降低了20%。

三、模型构建和数值模拟

前文的TFP测算结果显示,在控制资本利用率后,中国TFP的过度顺周期现象得到了改善。本部分通过构建内生增长DSGE模型,从模型脉冲响应角度,以货币政策冲击这一典型冲击为例,分析资本利用率在TFP变化中的作用。作为分析的延伸,这一部分还进一步探讨了货币政策冲击对TFP的影响效应,并进行了相关的稳健性检验。

(一)模型构建

1.家庭部门

考虑一个供给差异化劳动的代表性家庭,假设代表性家庭对消费和劳动的偏好可分:

(1)

家庭的跨期预算约束为:

(2)

Wj,t表示第j种差异化劳动的工资,τL,t表示劳动税平均税率,Tt表示政府的转移支付,Bt、St分别表示本国政府债券以及家庭在金融中介部门的存款,Rt表示无风险名义毛利率。Ct表示家庭的消费量,PC,t表示消费品价格,τc,t表示消费税平均税率。家庭通过选择消费、债券购买量、存款以及差异化劳动工资以及供给量来最大化终身贴现效用。

2.企业家

现实生活中,家庭不负责积累资本,遵循一系列金融摩擦相关研究的设定,如Christensen等[3-4]的研究,本文假设企业家充当资本品生产商和最终产品生产部门的桥梁,负责资本积累。在t期,企业家从金融中介那里以边际外部融资成本ft+1借入资金,从资本品生产商那里购入用于下一期生产的资本Kt+1,并将资本品以资本租赁价格RK,t+1借给最终产品生产商。在现实生活中,生产性资本的积累速度非常缓慢,而产出的变化非常迅速,为了使模型更贴近现实,本文引入资本利用率uK,t+1,则(1-δ[uK,t+1])Kt+1为折旧后的资本品。企业家的成本为ft+1(QtKt+1-Nt),Nt为企业家的净资产,则QtKt+1-Nt为企业家的资金需求。企业家在t期决定资本需求Kt+1、资本使用率uK,t+1,通过选择资本购买最大化收益。

3.资本品生产商

资本品生产商在t期决定第t+1期的资本品供给Kt+1,资本品生产商在t期末从企业家那里购买折旧后的资本品(1-δ[uK,t])Kt,使其与新的投资It相结合,形成Kt+1。参考Greenwood等[5-7]的研究,本文假设资本生产技术为以下形式:

(3)

4.金融中介

遵循Christensen等[3]对金融中介的设定,金融中介从家庭部门以无风险利率获得存款,根据企业家的杠杆率设定对企业家的名义贷款利率(或者边际外部融资成本)。

5.最终产品生产部门

遵循DSGE模型的一般设定,本文假设第i种差异化最终产品生产企业的生产函数取以下形式:

(4)

6.专利中间品生产部门

差异化专利中间品生产部门从研发部门购买无形专利生产有形差异化专利中间品,由于专利品存在差异性且具有垄断势力,因而通过设定价格使得利润最大化。与Kung等[8]的设定一致,本文假设中间差异化专利品使用1单位最终产品产出1单位差异化专利中间品。因而,对第j种国内差异化专利中间品生产商而言,其目标函数为:

Πj,d,t=maxPj,d,tGj,d,t(Pj,d,t)-PtGj,d,t(Pj,d,t)

(5)

其中,Pj,d,t和Gj,d,t(Pj,d,t)分别表示第j种国内差异化专利中间品的价格和需求函数。国内专利的垄断贴现价值为Vj,d,t=Πj,d,t+(1-φd)Et[Mt+1Vj,d,t+1],其中,φd表示国内专利的淘汰率。

7.专利研发部门

本文假设研发者将研发出的专利卖给专利中间品生产部门,获取专利的垄断贴现价值,则国内研发者的生产函数为:

Nd,t+1=νd,t(1+τR)Sd,t+(1-φd)Nd,t

(6)

其中,Sd,t表示国内研发者的投入,τR,t表示政府对国内研发者的资助比例。研发需要满足无套利条件,即研发1单位专利的成本等于收益,因而有:

(7)

8.政府

政府的跨期预算约束为:

Bt+1+(WtLtτL,t+PC,tCtτC,t+RK,tuK,tKtτK,t)+

(τI*,tPZ,tIF,t+τC*,tPZ,tcF,t)=BtRt+τRPtSd,t+

PtgtYt+Tt

(8)

政府在t期的收入由以下几部分构成:政府在t期发行的t+1期到期的1期名义债券,劳动税收、消费税收以及资本税收;支出由以下几部分构成:t期到期的名义债券的本息、对国内研发者的研发资助τRPtSd,t、政府支出PtgtYt,其中,gt表示政府支出的总产出占比,Tt表示转移支付。随着SLF、MLF和LPR等货币工具的常态化运作,中国货币政策调控框架正从数量型逐渐过渡到价格型。为体现经济运行现实,本文考虑三种货币政策:价格型、混合型和数量型。

价格型货币规则假定中央银行采用以下的泰勒规则设定基准利率:

εR,tr～N(0,(ωRr)2)

(9)

数量型规则参考Sargent等[9-10]的研究,设定货币规则为:

εR,tm～N(0,(ωRm)2)

(10)

卞志村等[11]指出,在中国现实的货币政策调控实践中,数量型和价格型货币政策工具并非非此即彼的互斥关系,二者呈现并存并重、协同发力的特征,表现为混合型货币政策规则。本文参考相关研究引入混合型货币规则:

εR,tmix～N(0,(ωRmix)2)

(11)

其中,γR为价格型成分在混合型货币政策规则中的相对权重。x∈{r,m,mix},分别对应货币政策的价格型、数量型和混合型。

国内产品市场出清条件为:

Yt=EXt+CH,t+gtYt+(1+τR)Sd,t+IH,t+

(12)

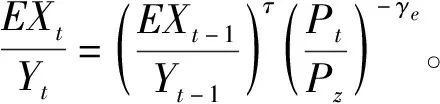
(二)内生全要素生产率

根据定义,全要素生产率是指各要素(如资本和劳动等)投入之外的技术进步和能力实现等导致的产出增加。理论上,资本存量和资本利用率共同构成的资本服务决定了生产函数中的资本要素投入部分,但是由于资本利用率数据不可得,在生产函数的资本要素部分,已有文献只考虑了资本存量部分。未控制资本利用率的全要素生产率与之类似,此处不再赘述,为此本文在控制资本利用率的条件下得到全要素生产率。本文用索洛余量定义全要素生产率,则模型的全要素生产率和产出可以表示为:

TFPt=

(13)

(14)

(三)参数校准与数值模拟

在求解模型前,本文先对模型中的内生增长变量做去势处理,在得到平稳变量后,进行参数校准,求解模型的稳态增长率,以及去除长期增长趋势变量的稳态值。在做脉冲响应分析时,定义去势变量围绕其稳态增长率的波动为短期波动,即定义传统意义上的经济波动为短期波动。本文同时考虑了变量围绕其稳态增长率的短期波动,以及变量含有随机趋势变量的增长率变化。模型在这部分的处理,符合对内生增长DSGE模型的常规处理方式。

1.参数校准

本文将主观贴现率设定为0.99,设定相对风险规避系数为1,将劳动供给弹性的倒数设定为1.2,将差异化劳动的替代弹性定为7[13]。在产品部门,设定参数ε为7,将参数φp设定为237.48;将参数α设定为0.3,将专利投入要素的收入份额γ设定为0.5[8],则由平衡增长路径的存在条件可得εd为0.6。在专利品生产部门,设定国内和国外专利中间品的淘汰率为0.037 5。在研发部门,通过设定参数χd使得模型稳态增长率符合中国2003—2017年的平均季度增长率均值2.35%,因此设定χd为0.033 2;设定专利的产出弹性ηd为0.83[8];使用贝叶斯方法对政府研发资助规则进行参数估计,使用《中国科技统计年鉴》数据,将稳态的资助比例取均值0.04。在资本品生产部门,将稳态时的资本利用率标准化为1,设定δ为0.025,以使稳态下的资本利用率为2.5%,将稳态时资本利用率的一阶条件设定为δ1;将δ2设定为0.01;将投资调整成本的系数κ设定为2[7];外部融资溢价弹性系数u一般设定在0～0.4之间。在政府部门,将稳态时政府名义债券占总产出比重设定为0.136 5,货币规则的参数估计结果见表1;在进口关税部分,根据世界综合贸易解决方案数据库(WITS)公布的中国平均关税率数据,将进口消费品和投资品关税稳态设定为11%和4.7%。在稳态时,消费占总产出比例约34%,国内研发投入占总产出比例为2.1%,贸易顺差占总产出比重约为1.4%,稳态增长率为2.35%,模型的稳态数据基本符合中国现实情况。

表1 不同货币政策调控框架的参数估计

2.数值模拟

本部分以货币政策冲击作为典型冲击,通过模型的脉冲响应函数,检验分析传统研究中因忽略资本要素利用率而导致的全要素生产率的过度顺周期性,以及中国金融市场的不完备性对中国全要素生产率顺周期性的进一步加剧。

假设货币供给增速经历1%的正向冲击,即宽松性货币政策,可以看到经济在短期围绕增长趋势经历了一个扩张的过程,模型的短期经济波动机制与传统的模型类似。货币宽松政策冲击后,无风险利率下降,导致企业家的边际外部融资成本下降,提高了企业家的资本需求;企业家资本需求的提高拉动了资本品价格以及资本品生产商的投资品需求,提高了经济的总需求。

由图5中TFP增长率的脉冲响应结果可以看到,1%的货币供给宽松冲击发生后,控制了资本利用率测算的TFP增长率变化不显著,冲击后迅速收敛至0。而未控制资本利用率测算的TFP增长率变化幅度最高达到了1.8%,这说明未控制资本利用率测算的TFP增长率存在过度顺周期现象。同时还可以看到,由于金融摩擦放大了经济变量围绕增长趋势波动的幅度,金融市场不完备进一步扩大了中国TFP增长率的过度顺周期性。此外,货币供给增速的变化对长期变量,如消费增长率、产出增长率的影响较小,变量在冲击后快速收敛至0。

图5 货币供给增速冲击结果(1%的正向宽松冲击)

当货币政策经历1%的正向冲击后,资本利用率最高上升2%,呈现出高度顺周期性。由于资本利用率被包含在传统的测算方程中,遗漏资本利用率测算的全要素生产率呈现过度顺周期性,遗漏变量测算的TFP增长率下滑幅度与产出增长率下滑幅度类似,而控制资本利用率的全要素生产率,即使在金融摩擦程度较高的情况下,其波动也显著小于产出增长率下滑幅度。

此外,数值模拟结果还发现,金融摩擦不仅放大了经济围绕其随机增长路径的波动幅度,同时也放大了研发投入的短期波动,金融摩擦对经济各变量包含其随机增长率的增长波动也存在放大作用。也就是说,中国金融市场的不完备性扩大了中国全要素生产率顺周期性。已有金融摩擦相关研究仅仅着眼于其对变量的短期波动影响,本文的发现填补了相关研究的空白。

综上,数值模拟结果显示:经济遭受外生冲击引起周期性变化时,由于资本利用率是高度顺周期变量,遗漏资本利用率的索罗余量实际包含了资本利用率一项,因而遗漏资本利用率放大了全要素生产率的周期性,最终导致全要素生产率的测算过度顺周期。与此同时,中国金融市场的不完备性,即金融摩擦机制,放大了全要素生产率的周期性;进一步分析货币政策对技术增长的作用后发现,当控制了资本利用率后,TFP测度不存在显著变动。

3.稳健性检验

随着SLF、MLF和LPR等货币工具的常态化运作,中国货币政策调控框架正从数量型逐渐过渡到价格型。为了体现经济运行现实,使得分析结论更具有稳健性,首先,本文在货币政策调控转型的背景下进行稳健性检验。混合型货币规则和价格型规则1%的扩张性冲击脉冲响应结果(图6)显示,货币政策冲击后,顺周期资本利用率短期迅速上升,带动短期产出的扩张。另外,长期变量(如产出增长)在扩张了0.1%后,迅速收敛。控制了资本利用率之后的TFP增长率对货币政策响应不显著,TFP只出现了1期正响应,且规模不显著。稳健性检验与前文结果一致。

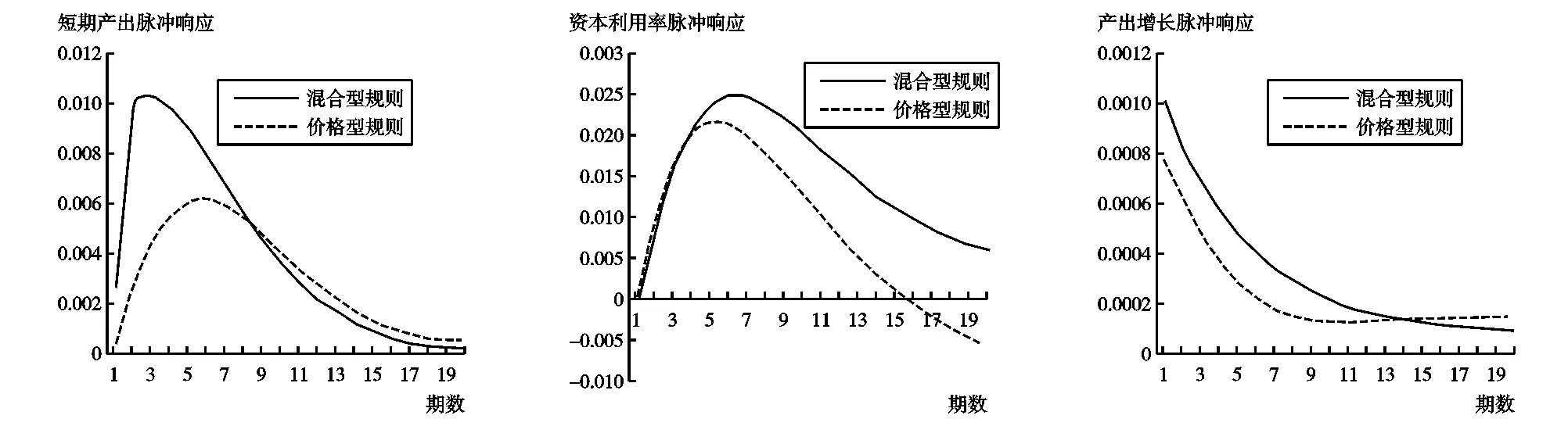
图6 稳健性检验结果(不同货币规则下1%宽松货币政策的脉冲响应)

其次,在基准模型中将生产函数的专利生产要素份额参数γ设定为0.5,α设定为0.3,根据模型的平衡增长路径存在性条件α+γ(1-εd)/(εd(1-γ))=1,确定εd为0.6;在研发的生产函数部分,将专利的产出弹性ηd确定为0.83。同时,对专利生产要素份额参数γ、专利的产出弹性ηd设定更多的赋值情况(γ=0.3,0.6,εd=0.4,0.5)以考察结论的稳健性。为了与前文保持一致,本文考察了货币供给量1%正向冲击。脉冲响应结果(图7)显示,在不同的参数设定下,上文结论具有稳健性,TFP对货币政策的响应快速收敛到0,货币政策对TFP的效应不显著。

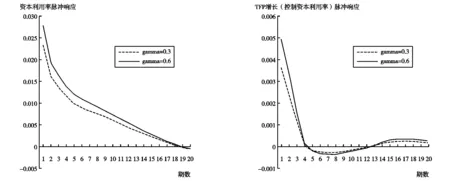
图7 稳健性检验结果(对参数赋值)

四、结论

长期以来,测算中国全要素生产率的研究普遍存在遗漏资本利用率的问题。本文认为,自1978年改革开放以来,中国的资本利用率变化较大,改革开放后经历了先上升后下降的过程,遗漏资本利用率测算的中国TFP存在严重偏误。本文通过基本事实和内生增长DSGE模型证明,遗漏资本利用率将导致TFP过度顺周期,使得TFP测算结果与经济波动高度正相关,并且在经济扩张时夸大技术进步率,而在经济收缩时低估技术进步率。使用模型数值模拟的结果说明,如果在测算生产率时遗漏了相关的投入要素利用率,那么即使生产率本身没有发生变化,生产率的测算结果也可能呈现出顺周期性。本文测算并比较了控制资本利用率前后的中国TFP增长率,结果发现:(1)在控制资本利用率后,中国TFP的过度顺周期现象得到了改善,TFP增长率的周期性成分波动性降低了20%。(2)未控制资本利用率的中国TFP测算结果高估了中国在1978—2000年间的技术进步率,低估了中国自加入WTO以来的技术进步率。控制资本利用率的中国TFP测算结果显示,改革开放在初期对中国技术进步的提升作用远远小于其对资本利用率的作用,并且2000年后中国贸易自由化和投资自由化极大提升了中国的技术进步率。(3)中国自经济体制改革以来全要素生产率增长呈现上升趋势。(4)在目前中国产能过剩的背景下,遗漏资本利用率的TFP测算结果将大大低估中国的实际技术进步。根据本文的以上发现,已有的研究结论需要重新评估。