数学建模教学培养学生核心素养

高杰

数学建模是应用数学知识对现实问题构建数学模型，并应用数学语言对实际问题进行描述、解决的方法。小学生年龄小，认知能力及实践能力有限，在学习抽象复杂的数学知识时感到难度较大，因此需进行小学数学建模教学，培养学生建模意识，提升学生解决实际问题的能力。

学生是参与教学活动的主体，在开展小学数学建模教学时，教师应注意从学生角度出发，结合小学生思维特征及生活经验，促进学生数学建模能力得到进一步发展。学生在学习数学建模的过程中既能够获取相应的数学知识，又能使自身数学观念、意识得到进一步强化。在这一过程中还可提高学生解决数学问题的能力，从而使数学核心素养培养目标得以实现。

开展教学活动时，数学教师需注意结合教材，进行数学思想方法的挖掘，并进行相应教学方案的设计。教师要充分考虑教学方案的科学性及实用性，通过创造实际问题情境的方式，渗透数学模型思想。例如，数学教材中的诸多知识均蕴含了“假设”这一数学思想，在“鸡兔同笼”问题的解决过程中应用假设思想后，计算更为方便。

首先，教师要使学生学会将现实问题转化为直观模型。教师在开展数学教学过程中要结合生活实际问题，应用直观实物给予学生引导，让学生体验和建立数学模型。其次，应用观察联想的方式，使学生更好地体会从直观模型到抽象模型这一过程。在开展数学教学过程中，教师应引导学生注意观察，展开充分联想，为学生建立抽象模型提供帮助，进一步提升学生的数学建模能力。最后，采用检验內化的方式，使学生更好地感悟抽象模型的自主建构过程。小学数学教师应为学生提供丰富的学习材料，为学生丰富感知体验过程提供引导，帮助学生在解决实际问题过程中感悟数学模型，内化后进行数学模型的构建。在这一过程中，教师既可了解学生对数学知识的掌握程度，又有助于学生体会数学模型的应用价值。具体操作过程如下：

一是设计相似问题，使学生数学建模意识得以强化。数学教学过程中，并非每次教学都应用情境教学，但需要教师应用情境导入教学内容，通过创建与实际情况相符的虚拟情境这一方式，来帮助学生在类似情境中感受数学模型。因此，在实际应用数学模型解决问题时，教师为使学生数学建模意识得到进一步强化，可围绕某一数学模型持续进行类似情境的创建，使其形成一个系列问题。

在解决问题过程中，应用这一模式，教师需要给予学生引导，使学生能够发现解决问题的关键点，适时应用建模知识。例如，在开展“分数的认识”（人教版）教学时，教师可采用折纸方式。首先，将一张长方形纸对折，将其平均分为2份，每一部分均为长方形的;其次，将对折的长方形再次对折，可将其平均分为4份，每一部分均为长方形的;再次，对折长方形，可将其平均分为8份，每一部分均为长方形的;最后，教师再引导学生将一盒月饼平均分成若干份、将一条线段平均分成若干段，并应用数学符号进行表示。这些问题均具有一定类似性，针对这部分问题，教师将其串联后进行总结，应用分数数学模型帮助学生更好地了解分数的意义。

二是创建问题情境，拓宽学生数学建模视野。在开展小学数学教学过程中，教师应注意引导学生进行数学模型的构建，帮助学生更好地感知数学模型的意义，让学生掌握数学模型中包含的共同结构，探究发现各个问题之间的共同特征，最终使学生掌握正确辨别、提炼模型的能力。同时，教师要培养学生归纳、解决问题的能力。教师在开展教学时要设计、鉴别、挑选恰当的问题，并应用不同方式呈现，在设计问题时渗透建模意识，使问题能够引起学生的探究欲望，同时也应注意问题的代表性。学生在分析、归纳情境问题的过程中，能够发现解决问题的关键，并主动应用数学模型解决实际问题，拓宽视野。

例如，学生在掌握了路程、速度及时间三者关系后，可进行“速度×时间=路程”这一数学模型的创建。具体来说，可采用变式练习的方式进一步巩固这一数学模型，以下面两题为例：（1）一列火车由甲地开往乙地，两地相距600千米，火车每小时行走75千米，火车需几小时能够到达乙地？（2）张叔叔从县城出发到某村送化肥，去时的速度是40千米/时，去时用了6小时，回县城时用了4小时。县城到该村的路程有多远？返回时速度是多少？

学生能够计算出张叔叔返回时的速度，则证明其已掌握基本数学模型。虽然上述两个问题文字表达方式不同，解决问题方式也具有细微差异，但是二者的解答均需应用同一数学模型。学生在解决问题的过程中进一步锻炼了思维，同时达到了变式练习的学习目标。

三是创建生活情境，进一步丰富学生数学建模体验。教师在开展数学教学时所创造的情境应满足教学需求，因此要求教师具有创新意识，创设问题情境。同时，教师要保证问题情境与某一数学模型相符合，使学生建模能力得到进一步加强，既可进一步加深学生对知识的理解程度，又可提高学生建模意识，对数学模型学习展开进一步深化及升华，强化学生数学建模的应用意识。

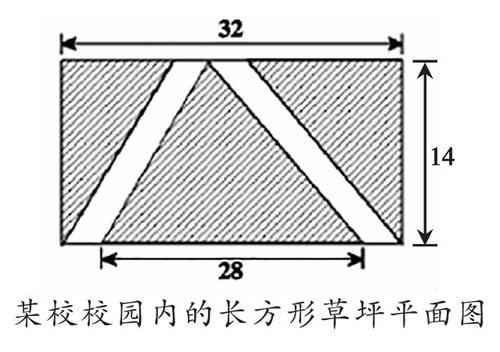
例如，在学习了“多边形面积”后，教师可应用实际问题情境的方式启发学生，围绕“草坪面积是多少？道路面积是多少？”等开放问题构建数学模型并进行数学计算。以下题为例：下图为某校校园内的一块长方形草坪，草坪中间有两条人行道，草坪宽度为14米，求草坪的面积是多少。（单位：米）

在解答例题过程中，学生能够进一步理解建立数学模型的意义，强化数学模型在实际问题中的应用。

数学模型的构建过程需逐渐进行抽象、提炼及概括。教师应对学生数学建模过程给予恰当引导，提高学生数学建模应用能力，提升学生数学思维水平，培养学生数学核心素养。

（责编 桑 涛）