基于射线模型的超声声速层析算法研究进展∗

朱 翔 田 超

(中国科学技术大学工程科学学院 合肥 230027)

0 引言

超声层析成像是一种根据穿透物体声波信号反演物体内部声学特性的成像技术，其可以分为反射型层析成像和透射型层析成像[1−2]。反射型层析成像通过探测被组织反射的声波信号，可以重建组织的阻抗特性。透射型层析成像通过探测穿透组织的声波信号，可以反演出组织的声学特性如声速度和声衰减。1974年，Greenleaf等[3]利用透射型超声层析成像实现了组织声学吸收的定量表征。超声层析成像提供的生物组织声速分布信息可以帮助医生区分正常组织和病灶部位[4−6]，在乳腺癌早期诊断等方面有重要作用[7−8]。

生物组织声速图像的重建通常利用透射超声波信号，如图1所示。环形超声换能器包围待成像生物组织，换能器阵元依次发射超声波信号，对面换能器阵元接收穿过组织的超声信号，并进行数据分析和反演重建[2,9−10]。除利用透射信号外，也有同时结合反射信号和透射信号进行组织声速分布重建的相关研究[11−14]。目前超声层析成像图像重建方法主要分为两类，分别为基于射线模型[15−18]和基于全波模型[19−23]的重建算法。基于射线模型的重建算法利用超声波的高频近似[24]，忽略了超声传播过程中可能的衍射和散射过程，认为声波在组织内近似沿射线传播。基于全波模型的重建算法通过求解波动方程来代替射线模型的高频近似，前向过程考虑到了声波的反射、衍射以及散射等物理现象，可以得到较射线类重建算法更优的图像分辨率。虽然基于射线模型的声速图像分辨率低于全波模型，但由于其数学原理简单，计算速度相对较快，在实际临床应用方面具有重要价值[25−28]。此外，基于射线模型的重建结果可以作为全波重建的初始值[21,29]，可以加快全波重建方法的收敛速度。

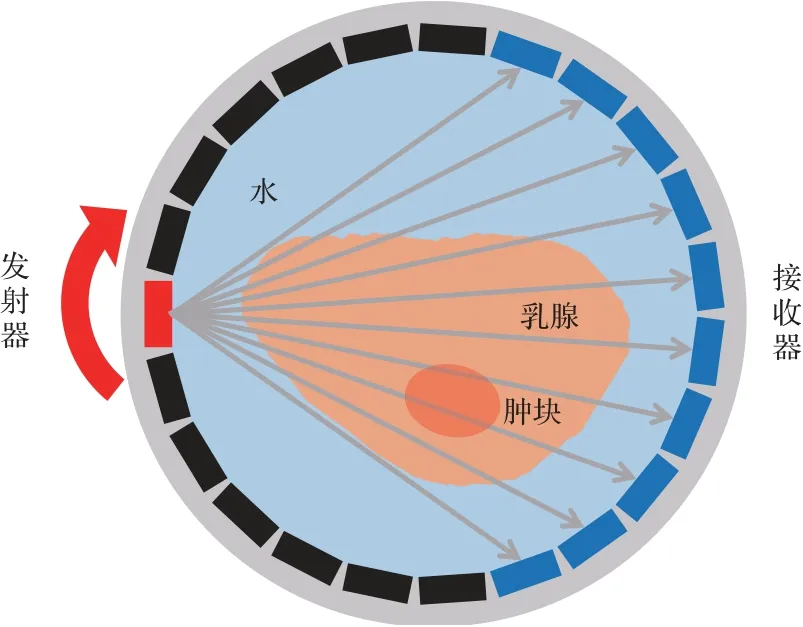
图1 透射超声层析成像原理图Fig.1 Principle of ultrasound transmission tomography

本文将首先介绍基于射线模型的超声层析成像前向过程，然后是基于射线模型的反问题求解方法，主要包括声波第一到达时间提取和图像重建反问题数学模型的建立和求解。

1 射线前向模型

声波传播的射线模型可以分为直线模型和弯曲射线模型两种。直线模型忽略了声波传播过程中的折射行为，认为声波完全沿直线传播。弯曲射线模型考虑了声波在不同界面处的折射过程，模型相对更加精确。本节将分别从直线模型和弯曲射线模型两个方面进行展开讨论。

1.1 直线模型

在直线模型的假设条件下，超声层析成像中的前向过程与计算机断层成像(Computed Tomography,CT)中的前向模型类似，如图2所示。其中，由发射器出射声波在接收器上的投影可以写为雷登变换形式：

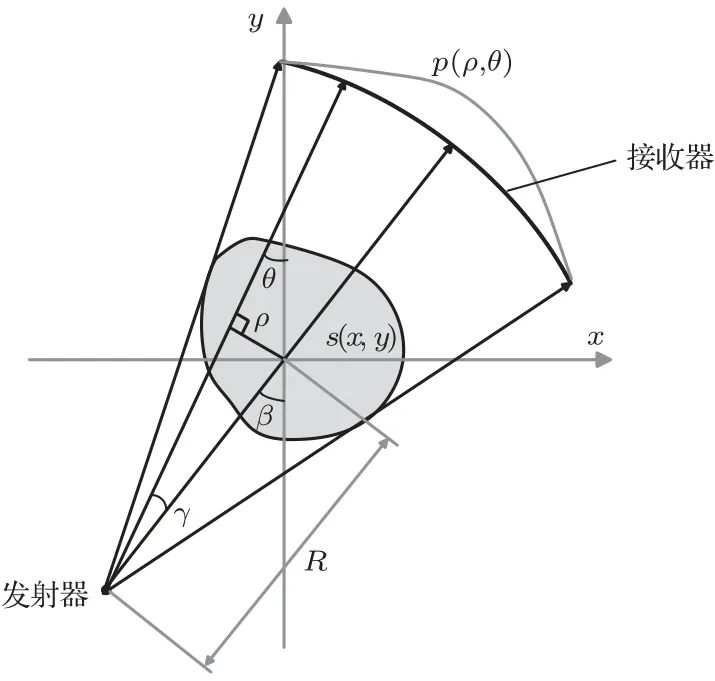
图2 超声层析成像中声波直线投影模型Fig.2 Straight ray projection model in ultrasound transmission tomography

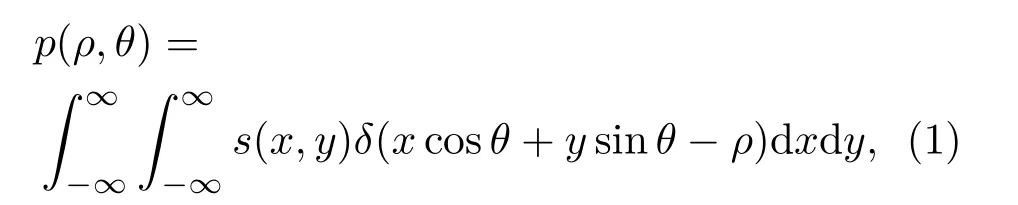
式(1)中，p(ρ,θ)为射线在角度θ情况下的声波第一到达时间，其中ρ表示坐标原点到射线的距离，s(x,y)为待测物体在空间坐标(x,y)下的声慢度(即声速度的倒数)分布，δ(·)为狄拉克冲激函数。实际超声换能器阵元近似以扇形束发射，可以先将射线的扇形束坐标(β,γ)转换成平行束坐标(ρ,θ)，即ρ=Rsin(γ)和θ=β −γ，然后再利用上述雷登变换进行计算。

直线模型可以近似描述声波的前向过程，但最终重建出来的图像在形状和数值上会存在较大误差，主要是因为直线模型忽略了声波在界面处的折射过程，最终导致射线积分路径错误。为此，可以引入弯曲射线模型校正直线模型存在的误差。

1.2 弯曲射线模型

近年来，基于弯曲射线模型的迭代重建算法不断发展，通过追迹声波的折射路径可以较好地校正直线模型引入的误差。相关研究表明弯曲射线追迹算法能够补偿介质中高达20% 的声速变化[30−31]。然而在典型的乳腺癌诊断中，乳腺中不同组织的声速变化大概为8%[32]。因此，可以利用弯曲射线模型较准确地描述组织声速差异引起的声波折射行为。

准确高效地追迹声波在组织中的传播路径，是基于弯曲射线模型图像重建方法要解决的关键问题。目前基于弯曲射线模型的射线追迹方法可以分为两大类，分别为全局法[33]和局部法[34]。全局法是基于程函方程的波前求解方法，而局部法则主要是基于射线方程的两点射线追迹方法，属于边值问题(Boundary value problem)。

1.2.1 基于程函方程的全局射线追迹

全局求解方法的关键在于程函方程的求解，主要为了确定声波的波前位置。其中程函方程可以表示为[35]

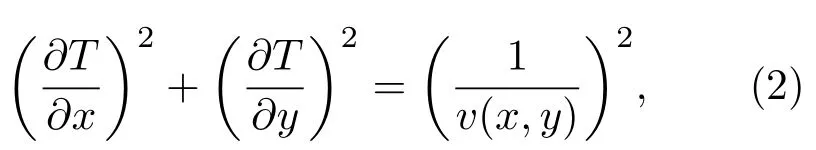
式(2)中，T表示声波到达时间的空间分布，v(x,y)表示声速的空间分布。程函方程的数值解法有很多，Vidale[36−37]将有限差分方法应用至程函方程的求解之中。Klimeš[38]随后在此基础上做了改进，将该方法推广至各网格点处到达时间以及慢度向量的求解，其可以同时计算出网格中心位置的到达时间和慢度向量，网格内其他位置的到达时间和慢度向量值可以利用四阶拉格朗日插值方法求得。该方法后来被美国卡尔马诺斯癌症研究所(Karmanos Cancer Institute)运用至超声层析声速重建的射线前向追迹过程中，用于重建乳腺组织的声速分布[32,39]。

近年来，程函方程的数值求解方法不断发展，快速行进方法(Fast marching method FMM)以其较高的计算精度和计算速度成为求解程函方程的重要手段[40−42]。图3显示了点源发射超声波信号经过圆形高声速区域时的声波传播轨迹。其中黑色虚线为利用FMM 方法计算出的等飞行时间分布曲线，即声波传播波前；黄色曲线为考虑非均匀声速分布时声波的实际传播路径；蓝色直线为不考虑非均匀声速分布时的直线传播路径。由图3可以发现声波经过高声速区域时，其波前会超前于背景声波的波前，产生畸变。

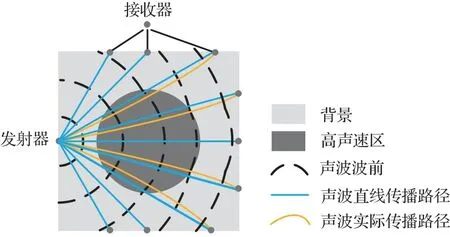
图3 基于程函方程的声波传播路径追迹Fig.3 Ray tracing based on the Eikonal equation

1.2.2 基于射线方程的局部射线追迹

基于程函方程的射线追迹是一种基于全局空间到达时间计算的方法。在三维成像时，该方法的计算量会显著增加并最终影响重建速度。利用基于射线方程的两点位置弯曲射线追迹方法，可以有效减少计算量，提高计算速度。射线方程可以表示为

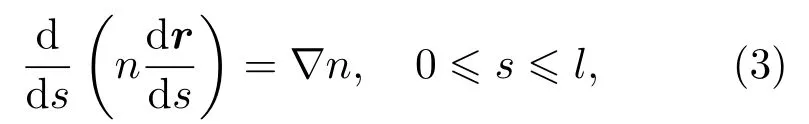
式(3)中，射线的起始点和终点分别为r(0)=a,r(l)=b。式(3)表明射线路径r(s)可以由离声源距离s、射线的起始位置a、终止位置b和介质的折射率n确定。求解二阶常微分方程式(3)的方法主要包括射线弯曲(Ray-bending)和射线链接(Ray-linking)两种方法。

在射线弯曲方法中，上述求解问题可以简化成已知两点位置的边值问题。通过固定射线的两个端点，迭代计算射线的传播路径，直到路径的变化小于一定范围[43−44]。据文献[45]报道，对于声速分布较为简单的组织，射线弯曲比射线链接更有效；但对于复杂的组织，射线弯曲的效率较低，有可能失败。

射线链接方法常用于两点之间的射线追迹问题。当射线的初始位置设置于发射点时，反复地调整射线的初始方向，直到射线的终点在一个很小范围内被接收点接收。将两点位置的边值问题转换成初值问题进行求解。Denis 等最早利用射线链接方法获取二维声波的弯曲射线路径[46]，总结出射线方程的不同求解算法，并用标准数值仿体测试不同追迹算法的性能，最终得出混合步长算法(Mixed-step algorithm)相比其他算法更有优势的结论[47]。后来，Javaherian 等[48]将射线链接方法应用至半球换能器阵列和任意三维换能器阵列中声波路径的追迹，将发射和接收阵元之间的射线追迹问题简化为求解最优起始方向的问题，并构建了相应的目标方程，将问题转化为

式(4)中，γ(e,r)表示发射点e到终点r的方向向量；γ(e,p)[de]表示发射点e在初始方向de的情况下，通过射线追迹得出声波路径到达终点p的方向向量。利用优化方法如高斯–牛顿法等求解目标方程，最终可以获得射线的最优初始方向de。

虽然射线链接方法常用于实际生物组织中的射线追迹，但依然需要不断地调整初始方向，使最终获取的方向和终点方向重合。对此，Qu 等[49]提出了不需要反复优化初始方向的射线链接方法。其基本思想为：首先定义射线的初始方向指向相应的接收阵元，然后根据空间折射率分布以及射线追迹方程，得到下一个步长∆s的空间位置，直至追迹至接收阵元。该接收阵元的位置可能会偏离实际物理接收阵元，此时称其为虚拟接收阵元。其中，射线追迹方程可以表示为

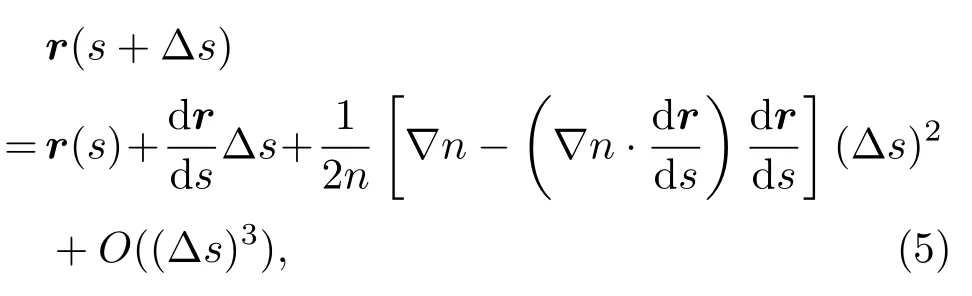
式(5)中，r和s分别表示方向向量和离发射位置的距离，n表示折射率。dr/ds可以用后向差分的形式表示，这样可以根据初始发射位置和初始发射方向，得到虚拟接收阵元的位置，如图4所示。最终可以根据实际接收阵元的空间位置和声波的到达时间信息，通过邻近阵元插值的方法估计出虚拟接收阵元的到达时间，进而反演空间声速分布。该方法避免了射线链接方法需要迭代优化初始方向的问题，可以有效缩短重建时间。

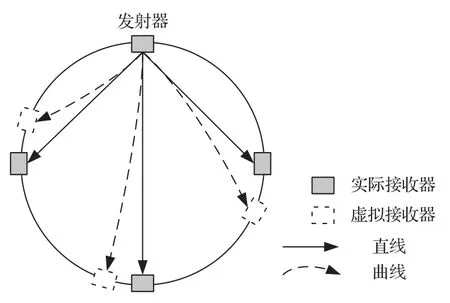
图4 虚拟接收阵元和实际接收阵元位置示意图Fig.4 Schematic diagram showing the distribution of virtual receivers and actual receivers

2 声速重建算法

第1节讨论的基于射线模型的前向过程可以获得理论上声波透过组织后到达换能器的时间。通过比对该理论到达时间与实验到达时间，构建合适的数学模型，可以反演声速的空间分布。

2.1 第一到达时间提取

为了重建声速分布图，需要首先获取声波透过组织到达接收换能器阵元的第一到达时间分布数据，即投影数据。由于超声层析成像中的数据量巨大，手动提取声波第一到达时间的方法是不切实际的，需要可以自动提取声波第一到达时间的算法。声波第一到达时间自动提取的方法最早出现于地球物理学科中的地震波成像[50]，随后被移植到医学超声层析成像中。目前主要可以分为3 种方法，分别是赤池信息量准则(Akaike information criterion AIC)算法[51]、互相关法[52]和能量法[53]。

AIC 算法通过检测第一到达时间前后信号的差异性，可以估计第一到达时间[51]。数学模型可以表示为

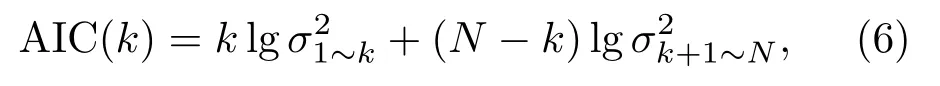
式(6)中，σ21～k和σ2k+1～N分别为声波信号采样点[1,k] 和[k+1,N]两段信号的方差值，N表示感兴趣声波信号区域内的采样点数。AIC取值最小的点可以作为声波的第一到达时间点。为了解决超声层析成像中的问题，Li 等[54]在原有AIC 算法的基础上，提出了改进的到达时间自动提取算法。改进主要体现在两个方面：(1)用权重平均模型代替了AIC 算法中的最优模型，在求解精度上更接近于真实情况；(2)对投影数据进行中值滤波去除异常值，有效抑制了投影噪声引入的图像伪影。互相关法利用互相关运算得到感兴趣信号和参考信号到达时间的偏移量，可以计算出感兴趣信号的绝对到达时间[52]。但是，当感兴趣信号和参考信号之间存在较大波形变化时，互相关方法的有效性会面临严峻挑战。对此，Qu 等[55]在AIC 提取到达时间的基础上，结合相邻换能器接收声波信号的相似性，利用互相关的方法求出相邻阵元接收声波信号的相对时间差，并校正AIC提取数据，可以得到较好的结果。能量法通过计算声波信号能量，将能量最先发生变化的地方，作为声波的第一到达时间[53]。该方法需要设定合适的阈值探测能量最开始波动的位置，在实际应用中易被噪声干扰，较少采用。

2.2 基于直线模型的滤波反投影重建

超声断层成像中最简单的声速重建方法是X射线CT成像中经典的滤波反投影(Filter back projection,FBP)算法。FBP算法基于超声的直线前向模型假设，数学模型可以表示为

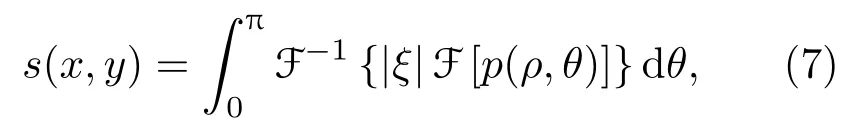
式(7)中，p(ρ,θ)为直线角度为θ时换能器阵元接收声波信号的第一到达时间，|ξ|为滤波函数，F 和F−为一维傅里叶变换和反变换，s(x,y)为最终重建的空间慢度分布。根据扇形束至平行束的转换关系，利用FBP 算法可以重建出生物组织声速度的空间分布。Greenleaf 等[56−58]最早开展基于FBP 的超声层析声速重建，可以得到初步的成像结果。

图5为利用FBP 算法对乳腺数值仿体重建的结果。可以看出，FBP重建结果存在较大误差，这主要是由于FBP 算法中的声波直线模型的假设所致。尽管如此，FBP重建结果可以作为弯曲射线迭代算法和全波反演算法的初始分布值，可以加速其收敛速度。

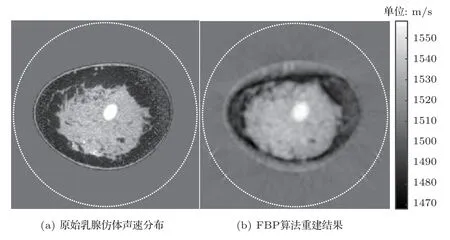
图5 基于直线模型的FBP 图像重建Fig.5 Image reconstruction using the FBP algorithm

2.3 基于弯曲射线模型的迭代重建

利用声波的直线模型假设和FBP 算法可以重建出组织的初始声速分布。但由于实际生物组织的非均匀性，声波在不同组织界面处会发生折射，弯曲射线模型相较于直线模型可以更好地描述该种情况下声波的传播轨迹。如图6所示，基于弯曲射线模型重建结果相对于直线模型重建结果(图5)更加准确。下面将主要介绍基于弯曲射线模型的迭代重建算法。

实践证明，“因材施教、分层培养、工学交替、强化技能”的人才培养模式及课程体系是高职机制专业改革的一条可行之路，较好的解决了高职学生学习积极性不足、技能优势不明显的问题。至于工学交替实训及课程体系中存在的一些瑕疵，有待在实践中予以完善。

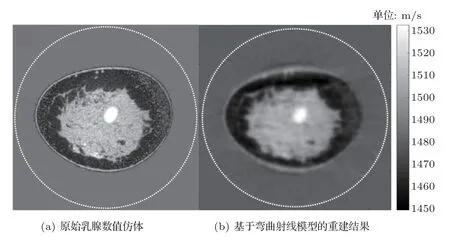
图6 基于弯曲射线模型的重建结果Fig.6 Image reconstruction based on a bent-ray model

2.3.1 数学模型

基于弯曲射线模型的迭代重建算法原理如图7所示。待成像区域被离散成一定大小的网格，环形超声换能器阵列中的一个阵元发射超声信号，超声波在经过不同声速区域时会发生折射，最终到达接收阵元。超声波的折射过程可以利用弯曲射线表征。

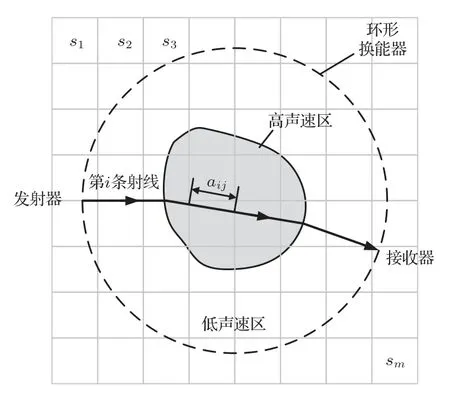
图7 基于弯曲射线模型的迭代重建原理Fig.7 Schematic diagram showing the principle of iterative reconstruction based on bent rays

图7中线段aij表示i条声波射线在第j个网格内的截距，即权重因子。由此，每一个发射接收对之间的声波射线可以用一个线性方程表示，即

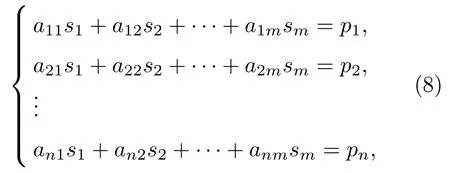
式(8)中，p表示声波射线的第一到达时间，s为待重建生物组织的慢度(声速的倒数)。式(8)也可以写为矩阵形式，即

式(9)中，p为声波的第一到达时间向量；s为待重建组织的慢度向量；A为联系两者的系数矩阵，其包含了声波射线传播的路径信息，和换能器的空间分布以及组织的慢度分布s直接相关。

声速的重建过程需要引入射线轨迹校正步骤，在每次的慢度分布更新之后，需要根据更新后的声速分布重新校正声波的射线轨迹。由此，超声层析成像中声速重建的基本流程如图8所示。

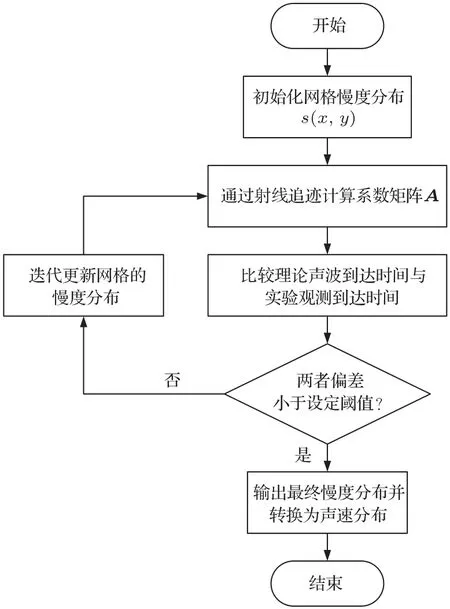
图8 迭代重建算法流程图Fig.8 Flow chart for iterative image reconstruction

在图8中，为了得到稳定的声速分布，需要不断比较基于弯曲射线模型的理论声波到达时间和实验观测到达时间。下面主要讨论目前应用于超声声速层析成像的迭代数学模型。

2.3.2 代数迭代算法

求解式(8)最简单的方法是利用X 射线CT 中代数迭代算法(Algebraic reconstruction technique,ART)对每条声波射线经过的网格慢度进行校正[30]。可以表示为

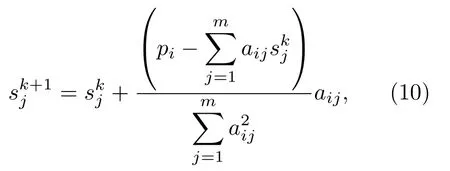
式(10)中，skj为第j个网格在第k次迭代时的慢度，pi为第i条射线的到达时间，aij为射线经过网格的长度信息，m为网格总数目。由于实际超声换能器阵元数目较多，系统中的声波射线数目庞大，式(10)所表示迭代过程相对较慢。Li 等[24]和Denis 等[46]采用联合代数迭代算法(Simultaneous algebraic reconstruction technique,SART)加速传统代数迭代算法，将每一个投影角度下的射线视为一组，可以提高重建速度。

2.3.3 正则化迭代算法

将基于弯曲射线模型的离散矩阵方程式(9)改写为最小二乘形式，可以构建出非线性目标方程：

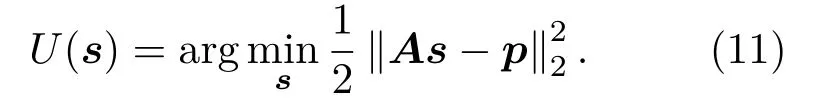
式(11)中，U(s)为关于慢度s的目标方程，寻找合适的慢度分布使得最小二乘目标方程取得最小。最常用的解法是高斯牛顿法[59]，可以不断迭代更新慢度值s。但通常系数矩阵A为稀疏矩阵并且具有很大的条件数，使得原目标方程具有病态性。当噪声增加时，将会引起重建结果的不稳定。针对该问题，可以通过添加正则化约束改善问题的病态，稳定解空间。由此，目标方程可以改写为

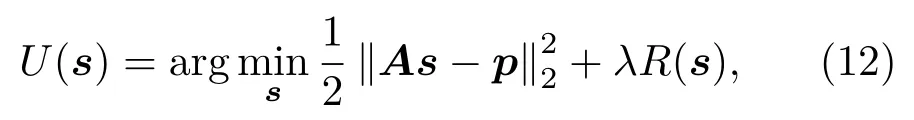
式(12)中，R(s)为正则函数；λ为正则参数，主要用于调节正则项的权重。Hormati 等[60]采用稀疏正则函数来表示R(s)，可以有效降低重建图像的背景噪声。Li 等[32]于2009年将TV 正则约束应用于超声声速层析重建中，并与Tikhonov正则约束重建结果进行了比较，得到TV 正则约束可以保持图像边界信息的结论。Intrator[61]和Huang等[62]针对TV正则和Tikhonov 正则各自的优势，将两者进行融合，可以兼顾Tikhonov 正则的噪声抑制性能和TV正则的图像边界信息保持功能。

2.3.4 统计迭代算法

迭代方法中另一类重建算法是基于统计思想的图像重建方法。将整个超声换能器接收到的声波数据看成满足一定条件的统计分布，可以将重建问题转化为由随机变量到达时间数据估计图像慢度分布的问题。其中极大似然估计(Maximum likelihood,ML)是一种运用比较广泛的算法，通过期望最大化方法(Expectation maximization,EM)求解极大似然模型，再通过迭代过程求解最终解。其中，迭代公式可以表示为[63]

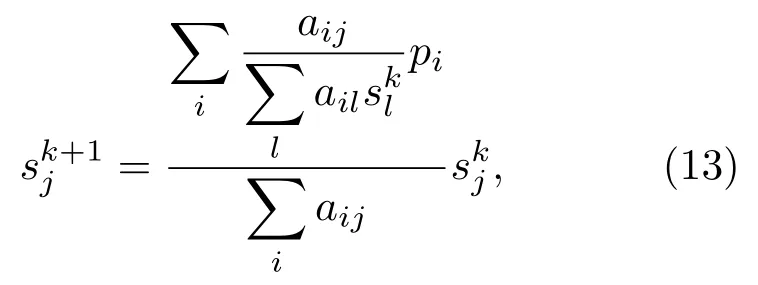
式(13)中，为第j个网格第k+1次迭代的慢度值，pi为第i条声波射线的第一到达时间，aij为射线经过网格的长度信息。Merčep 等[64]和Perez-Liva等[31]基于ML-EM 算法利用每一对发射接收阵元的投影数据校正上一次的慢度分布，可以得到更新的慢度空间分布。在噪声比较大时，ML-EM方法直接迭代求解会出现不稳定性。由此，Merčep 等[64]在ML-EM算法迭代过程中加入了基于中值的先验信息，最后形成后验分布即贝叶斯表达式。该思想类似于在最小二乘方程中添加正则约束。此外，Ali等[65]通过贝叶斯表达式加入了图像的先验信息，最终可以得到慢度的迭代模型，进而求解声速的空间分布。先验信息的引入可以加速重建过程的收敛速度，稳定解空间。

3 结论与展望

本文综述了基于射线模型的超声层析成像中声速重建算法最新研究进展，总结了直线和弯曲射线的前向模型，讨论了声波第一到达时间提取的不同算法。此外，综述了图像重建反问题数学模型的建立和求解方法，主要包括基于直线模型的滤波反投影重建和基于弯曲射线模型的迭代重建。基于弯曲射线模型的迭代重建中主要讨论了代数迭代算法、正则化迭代算法和统计迭代算法。为了解决数学模型中的病态问题，可以在目标方程中加入正则项或先验信息，以稳定解空间，加速解的收敛速度。

通过超声声速重建算法的综述，基于射线模型的声速重建算法预计未来将着重向以下几个方向发展：

(1)目前弯曲射线的追迹算法主要应用于二维超声换能器中，三维换能器中弯曲射线追迹问题尚在研究中，开发出能够在三维超声换能器中快速实现弯曲射线追迹是一个重要的研究方向。基于两点的射线追迹算法可能可以成为三维射线追迹的重要突破口。

(2)从原始声波信号中提取的第一到达时间是声速重建中重要的输入数据，它的精度直接影响最终的图像重建质量。尽管目前现存的第一到达时间提取算法具有较好的性能，但是在处理较大噪声数据时，仍然存在提取到达时间错误的情况。发展更鲁棒的第一到达时间提取算法是未来发展的一个重要方向。

(3)最后是基于射线模型的声速重建数学模型的建立问题。由于实验中超声换能器阵元数量有限，往往会出现待重建区域声波射线密度不足的问题，使得重建结果不稳定，为此需要发展更加鲁棒的数学模型。