基于遗传算法的水电站有效库容优化方法

韩友春,金丛成

(江苏禹衡工程质量检测有限公司,江苏 盐城 224000)

0 前 言

中国南方部分地区深受洪水灾害影响，水电站作为防洪的重要设施，现有水电站有效库容能力不足导致水库水位低、弃水量较多、发电量不足[1-2]。目前依靠传统工程设施已经不能满足水电站库容的优化需求，因此，诸多学者为解决该问题进行可大量研究。付壮[3]通过构建优化调度模型，进行协调计算，得到库容优化的目标函数，利用惩罚函数，计算最优的容水量组解，利用大系统协调法对收敛条件以及分解过程进行深入的推导，该方法在一定程度上提升了水库的容水量，但是没有针对弃水量进行有效优化。马昱斐等[4]基于全微分法联合建立调度增益与时段弃水量,蓄量差的关系模型，采用全微分公式定量分解各水库增益贡献，挖掘水电站水库调度潜力，求解模型的离散性多阶段过程，拓宽模型的约束条件限制，得到水库群的最优调度规则，该方法针对弃水量和水位幅度进行了有效优化，但在水库发电量方面没有进行相关改进，水电站的有效库容优化不全面。

本文基于上述研究存在的问题，利用遗传算法构建水电站有效库容优化模型，提出基于遗传算法的水电站有效库容优化方法，并经实验证明该方法能有效优化水电站库容，提升水电站水库蓄放水能力。

1 利用遗传算法构建水电站有效库容优化模型

1.1 计算水电站有效库容优化的目标函数

采用同步蓄水的调度策略[5-7]，对各水库库容进行均衡分配，使其保持在一个相对平衡的状态，进而提高水电站有效库容。首先获取水电站有效库容优化的目标函数，将水电站的最小超标洪量，作为第一层目标函数。超标洪量Q的数学表达式为：

(1)

式中：η为水电站的防洪水库集合，座;T为水库同步蓄水的调度期时段总数，s;Δt为单位调度时长，s;Ai,t为i水库在t时段的入流量,m3/s。根据同步蓄水策略，把水库之间的库容使用率差值降到最小，并将其作为第二层目标函数。计算各水库的末库容使用率，其公式为：

(2)

式中：Di,t、Dj,t分别为i水库和j水库在t时段的末库容使用率,%;Vi,t、Vj,t分别为i水库和j水库在t时段的末库容,m3;Ei、Ej分别为i水库和j水库的汛限水位对应库容,m3;Fi、Fj分别为i水库和j水库的防洪库容,m3。则库容使用率差别G的数学表达式为：

(3)

式中：γ为水电站水库集合。根据公式(1)和(3)，将有效库容优化。转换为多目标优化调度问题，根据2个目标之间的竞争关系，使用无量纲法和权重法[8-10]，结合处理变量Q、G，合并量级存在差异的2个目标，建立有效库容优化的总目标函数minF，其数学表达式为：

minF=α(Q/Qmax)+β(G/Gmax)

(4)

式中：α、β为目标权重系数，分别取值为0.6、0.4;Qmax为水电站的理论最大超标洪量，m3/s;Gmax为水库库容使用比例之差的理论最大值，至此完成水电站有效库容优化目标函数的计算。

1.2 计算水电站有效库容优化的约束条件

计算有效库容优化的约束条件，对总目标函数minF进行约束。水库水量平衡约束条件的计算公式为：

Hi,t+1=Hi,t+(Mi,t-mi,t)×Ii,t

(5)

式中：Hi,t、Hi,t+1分别为i水库在t时段、和t+1时段的水库库容，m3;Mi,t为i水库在t时段的入流量，m3/s;mi,t为i水库在t时段的断面流量，m3;Ii,t为i水库在t时段的区间流量，m3。水库库容限制约束条件的计算公式为：

Ei≤Vi,t≤Fi

(6)

水库泄洪流量限制约束条件的计算公式为：

(7)

|ki,t+1-ki,t|≤Δkit∈[1,T-1]

(8)

式中：Δki为i水库的超标流量限制;ki,t+1、ki,t分别为i水库，t+1时段和t时段的超标流量，m3/s。水电站过洪能力限制约束条件的计算公式为：

qi,t≤Ji(Ki-Li)

(9)

式中：Ji为i水库保证水位对应的控制流量，m3/s;Ki为i水库的起调库容,，m3;Li为i水库的调度期末库容,m3。防洪安全约束条件的计算公式为：

qi,t≤Ni

(10)

式中：Ni为i水库能够允许的最大泄流量，m3/s。出力约束条件的计算公式为：

(11)

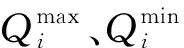
1.3 实现优化有效库容

根据目标函数和约束条件，建立水电站有效库容优化模型，对模型进行求解，得到库容最优分配策略。使用遗传算法对模型进行反复进化迭代，具体流程如图1。

如图1所示，将公式(4)作为遗传算法的目标函数，即种群迭代的适应度函数，采用离散库容的方式[11-14]，编码水电站有效库容，使库容实际值对应个体基因，将水位升降变化时对应的库容，作为基因段变化范围，得到遗传算法的初始种群。库容实际值Hi,t计算公式为：

图1 遗传算法的模型求解流程图

(12)

2 实验论证分析

进行对比实验，将此次设计方法记为实验A组，2种传统径流式中小型水电站有效库容优化方法，分别记为实验B组、C组。当有效库容优化后，利用水库水位提升幅度、弃水总量、发电量3个指标比较水电站水库的蓄水能力。

2.1 实验准备

选取江苏省内的某水电站为例，主要特征参数如表1所示。

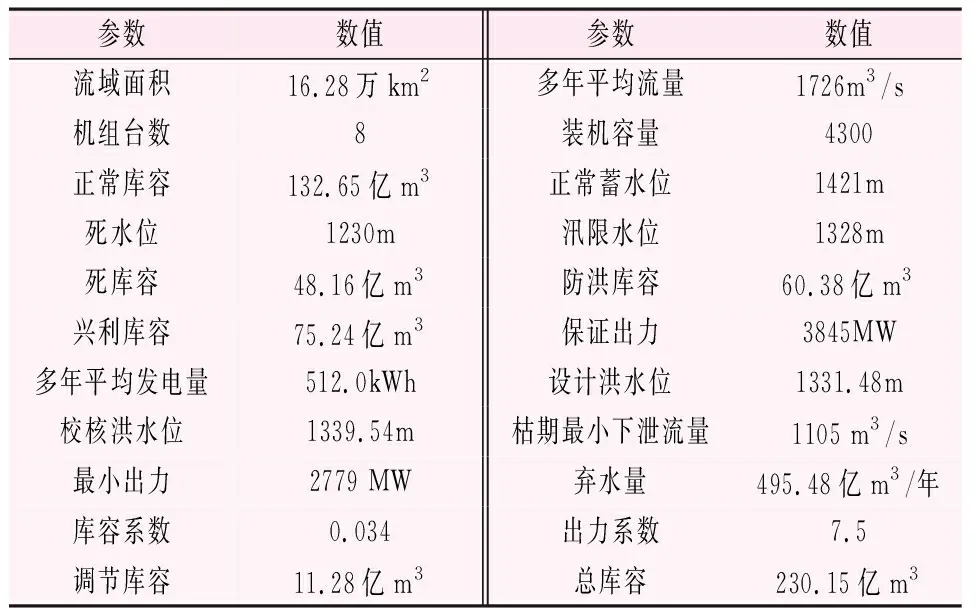
表1 江苏省某水电站特征参数表

某水电站群梯级示意如图2所示。

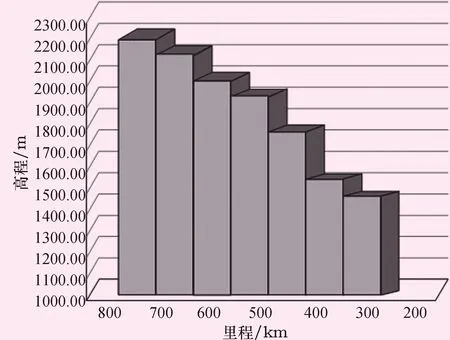
图2 阶梯水电站示意图

该水电站枯水年、平水年、丰水年3种不同的典型来水过程如图3所示。

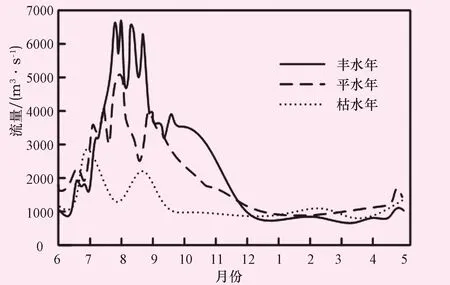
图3 水电站各典型年日径流过程图

根据该水电站2005—2020年相邻15 a的径流资料对水库容量进行优化调度。在3个典型年中，每月取3个典型日，将其流量过程作为需要分析的资料，典型日分别为日均流量与月平均流量最为接近的一天，当月日均流量最小的一天以及当月日均流量最大的一天。实验A组设置遗传算法的迭代次数为1 000，个体基因适应度值为0.9。

2.2 实验结果

2.2.1第1组实验结果

当3组方法优化后，划分水电站有效库容，比较水库水位的提升幅度，实验对比结果如表2所示。

表2 水库水位提升幅度对比结果表

由表2可知，有效库容优化后20 d内，实验A组水库水位平均提升幅度为197.02 m;实验B组、C组的平均提升幅度分别为152.34、130.90 m;A组水库水位相比实验B组、C组，分别提升了44.68、66.12 m。

2.2.2第2组实验结果

有效库容优化后，统计水电站每天的弃水总量，弃水量对比结果如表3所示。

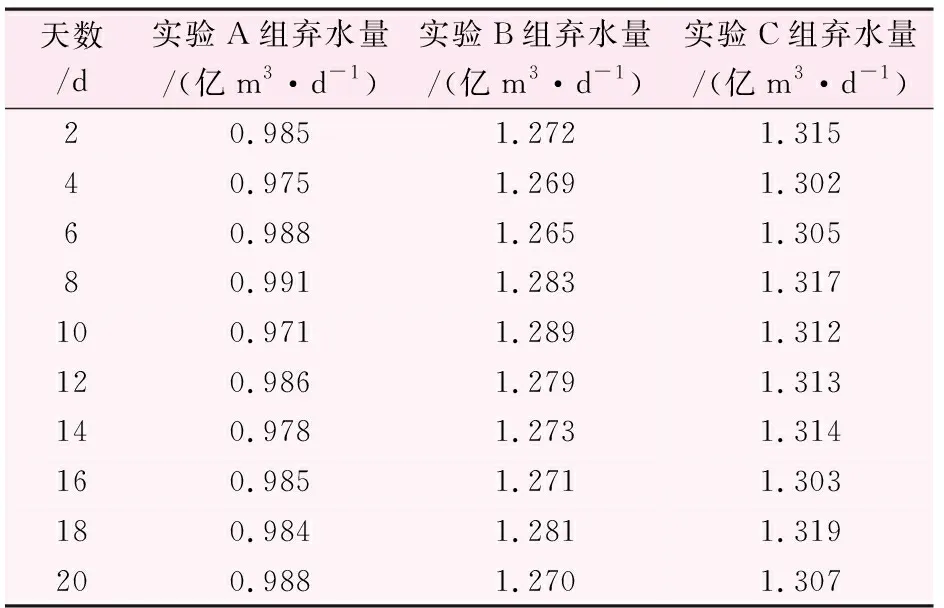
表3 弃水量对比结果表

由表3可知，有效库容优化后20 d内，实验A组平均弃水量为0.983亿m3/d;实验B组和实验C组的平均弃水量分别为1.275亿、1.316亿m3/d;相比实验B组和C组，A组水库弃水量分别减少了0.292亿、0.333亿m3/d。

2.2.3第3组实验结果

有效库容优化后，统计水电站每天的发电量，发电量对比结果如表4所示。

由表4可知，有效库容优化后20 d内，实验A组平均发电量为7.691亿kWh/d;实验B组、C组的平均发电量分别为6.889亿、6.570亿kWh/d;相比实验B组和C组，A组发电量分别增加了0.802亿、1.121亿kWh/d。综上所述，此次设计优化方法下，水库水位有较大幅度提高，减少了弃水量，从而抬高了限洪水线，水库蓄水量充足，保证了运行水位的下泄流量，进一步增加了发电量，水电站水库的蓄放水能力，要优于2种传统有效库容优化方法。

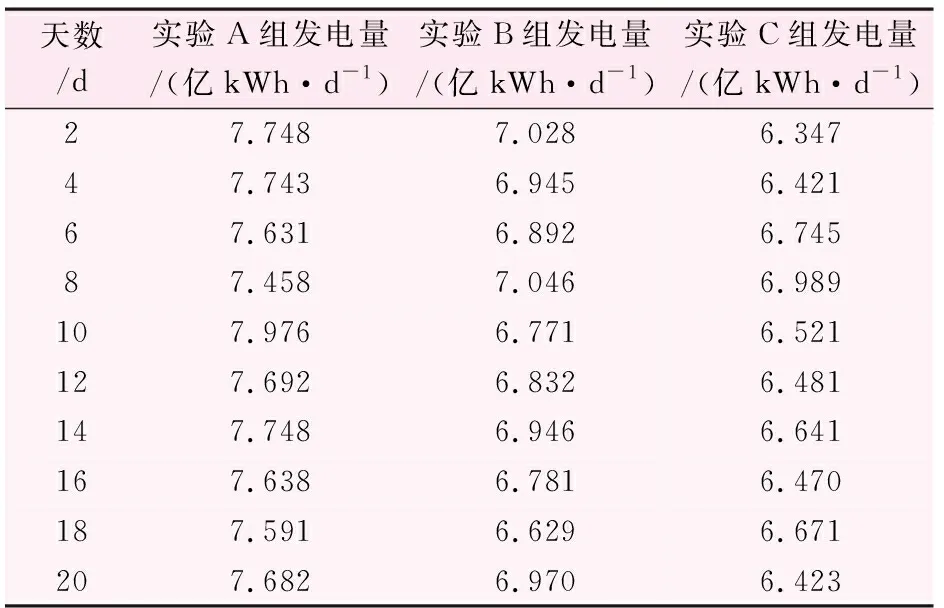
表4 发电量对比结果表

3 结 语

将水电站的最小超标洪量、水库库容使用率的最小差值，作为有效库容优化的目标函数，选取水库水量平衡、水库库容限制、水库泄洪流量限制、安全过洪能力限制等，对目标函数进行约束，建立有效库容优化模型，通过遗传算法求得模型最优解，均衡分配水库库容，得到优化后的库容实际值，实现了水电站有效库容优化，提升了水位量和发电量，减少了弃水量，具有一定的科学性。但此次研究中忽略了水库泥沙淤积的影响因素，在今后的研究中，应结合二维和三维水沙数学模型，对水电站有效容量进行合理划分。