二维函数光子晶体中的类Dirac点及带隙结构

任明丽, 杨涪铨, 刘 晗, 韩 梦, 朱翔久, 姜明奇, 吴向尧

(吉林师范大学 物理学院, 吉林 四平 136000)

近年来, 光子晶体材料在许多领域应用广泛. 如石墨烯被用作润滑剂, 由于其片状结构, 因此大量碳原子在同一平面内紧密结合, 在范德华力的作用下上下薄片间仅微弱附着, 这种弱的层间相互作用使提取原子或几层原子成为可能[1-2]; 二硫化钼(MoS2)已用于设计二维光源、 晶体管、 偏振选择器和光电探测器等光电器件[3-6]. 二维MoS2与块状材料相比, 其单层膜结构的直接带隙使光致发光得到加强[7], 得到了更小的有效激子Bohr半径(1 nm)和较大的激子结合能(0.96 eV), 为实现在室温下的激子器件研发提供了条件[8], 其偶极取向的二维特性使激子发射具有高度的各向异性[9].

与三维光子晶体材料相比, 二维光子晶体材料具有许多独特性能. 首先, 垂直于二维平面方向的量子局域产生了新的电学和光学性质, 这些性质与三维情形明显不同[10]. 其次, 二维材料的表面会自然钝化任何悬垂键, 从而使二维材料易与波导和空腔等光子结构集成. 由于异质结构中晶格常数不同的层与层状体材料的范德华力结合较弱, 因此使用不同的二维材料可构建垂直异质结构而不存在传统的晶格失配问题[11]. 最后, 由于二维材料的原子层较薄, 因此它们与光的相互作用更强[12].

在研究石墨烯的电子能带结构中提出了Dirac点[13-15], Dirac点通常出现在第一个Brillouin区内, 在带隙结构中, 上、 下导带间以线性方式相交, 产生一个Dirac锥, 在该点上, Maxwell方程组可被不含质量的Dirac方程取代[16]. 在光子晶体结构中可模拟石墨烯中的Klein隧道效应和Zitterbewegung效应[17-19]. 此外, Dirac点可研究光子晶体中的局域态模式, 称为Dirac模式[20]. 目前, 已对三角形、 蜂窝形、 阿基米德式和类蜂窝形晶格的光子晶体中Dirac模式进行了研究[21].

在正方形晶格的光子晶体Brillouin区中心存在线性色散关系. 半Dirac点是一类研究特殊电子带隙色散关系的新模式[22], 由能带在Brillouin区中心或边界上相交于一点形成. 在二维(2D)Brillouin区费米面的一个点附近, 色散关系沿对称轴是线性关系, 在垂直方向为二次形式, 研究表明, 该半Dirac点与半金属相和带绝缘体间的拓扑相变有关[23].

由A和B两种介质组成的一维函数光子晶体, 其折射率是关于空间坐标的函数[24-26], 与由介质折射率为常量的A和B两种介质构成常规光子晶体不同. 本文研究二维函数光子晶体横电(TE)和横磁(TM)波模式的带隙结构, 并在二维函数光子晶体中得到绝对带隙和类Dirac点. 当介质柱半径和介电常数的函数形式不同时, 带隙结构发生相应改变. 因此， 利用二维函数光子晶体可设计所需的带隙结构, 从而为光学器件的设计提供一种新方法.

1 二维函数光子晶体介电常数的Fourier变换

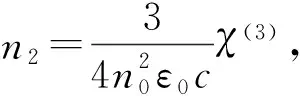
圆柱形介质柱的介电常数为

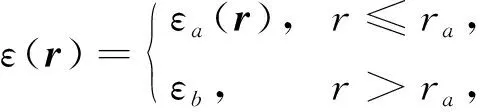
(1)

或表示为

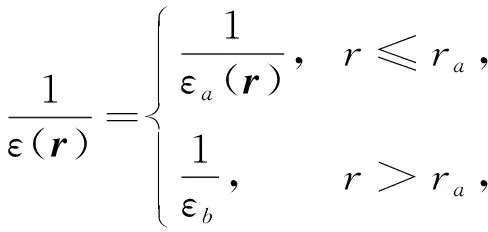
(2)

方程(2)可写为

(3)

(4)

(5)

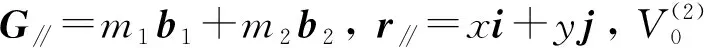
将方程(3)代入式(5)可得

其中

(8)

当|r∥|=r∥=r, |G∥|=G∥, dr∥=ds=rdrdθ时,r∥和G∥的夹角为θ.

由式(8)可得

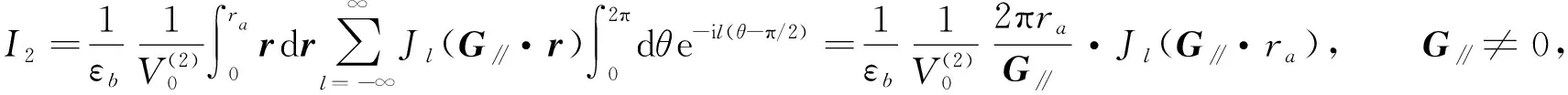
(9)

当G∥→0(m→0,n→0)时,

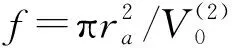
当G∥=0,J0(0)=1时, 由式(11)可得

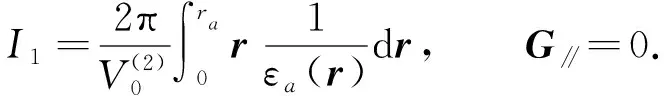
(12)

将I1,I2和I3代入方程(6)可得

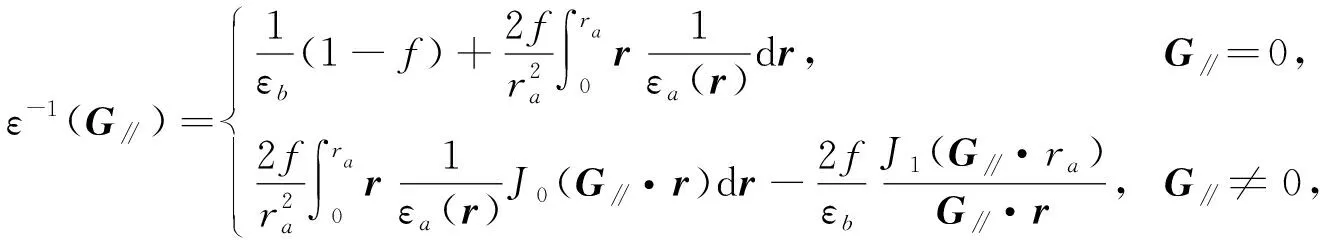
(13)

方程(13)称为二维函数光子晶体介电常数的Fourier变换.当εa(r)=εa时, 若εa为常数, 则方程(13)变为

(14)

方程(14)称为二维常规光子晶体介电常数的Fourier变换. 因此, 二维常规光子晶体是二维函数光子晶体的特殊情况.

用平面波展开法可得TM波和TE波的特征值方程[29-30]分别为

将式(13)代入式(15)和式(16), 可得二维函数光子晶体的带隙结构.

2 数值分析

下面分析二维函数型光子晶体带隙结构的数值结果. 分别用方程(13),(15),(16)计算二维函数光子晶体的带隙结构. 设该光子晶体为三角形晶格, 圆柱形介质柱位于空气背景板中. 研究介电常数是空间坐标的函数形式εa(r)=kr2+b(0≤r≤ra), 其中r为介质柱半径,k为函数系数, 当k=0时, 它是常规型光子晶体, 当k≠0时, 变为函数型光子晶体, 令k=3×1012,b为常数项.研究常数项b对函数光子晶体带隙结构的影响.

介质柱介电常数函数形式为εa(r)=kr2+b和b=8时三角晶格二维函数光子晶体TE模式和TM模式的带隙结构如图1所示, 其中k=3×1012, 介质柱半径r=0.4a.由图1可见, 当ωa/(2πc)=0～1时, TE波有5个带隙, TM波没有带隙. 由于在带隙结构谱中, 两层能带相交, 在一个方向上是线性的, 在另一个方向上是二次型的, 将这种交点定义为类Dirac点. 因此, 在TE波带隙中有A和B两个点为类Dirac点.

图1 介质柱介电常数函数形式为εa(r)=kr2+b和b=8时三角晶格二维函数光子晶体的带隙结构Fig.1 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants εa(r)=kr2+b and b=8

介质柱介电常数函数形式为εa(r)=kr2+b和b=9时三角晶格二维函数光子晶体TE模式和TM模式的带隙结构如图2所示, 其中k=3×1012, 介质柱半径r=0.4a.由图2可见, 当ωa/(2πc)=0～1时, TE波有5个带隙, TM波有1个带隙. 在TE波带隙中有A和B两个点为类Dirac点.

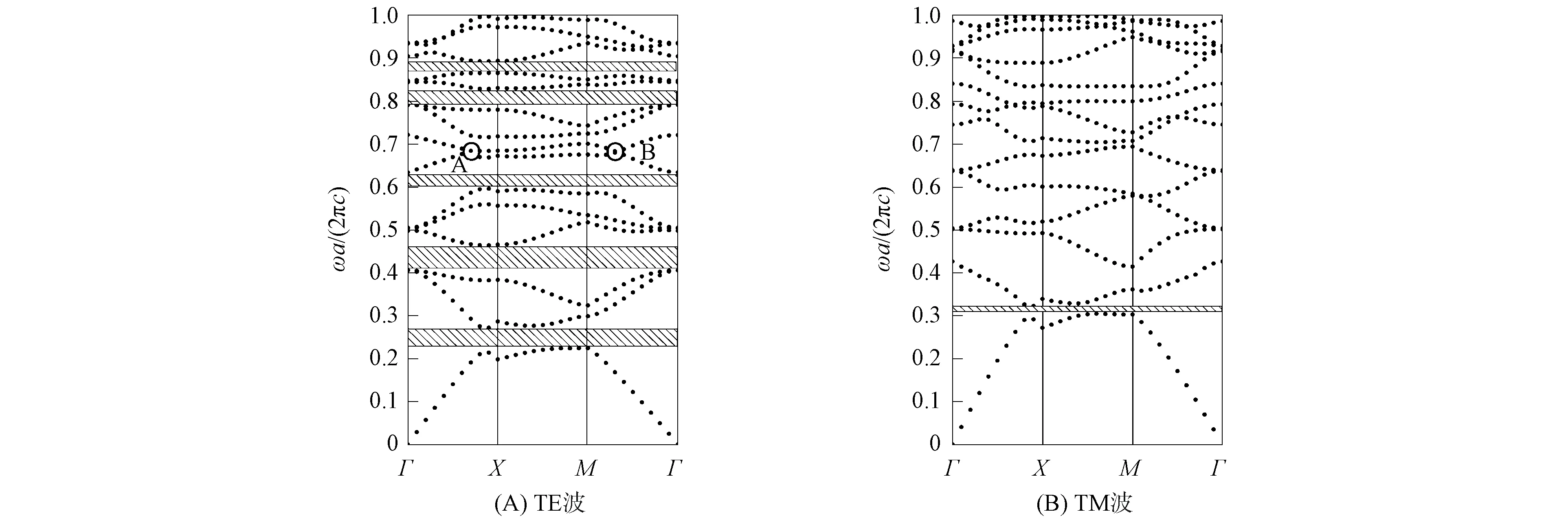
图2 介质柱介电常数函数形式为εa(r)=kr2+b和b=9时三角晶格二维函数光子晶体的带隙结构Fig.2 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants εa(r)=kr2+b and b=9

介质柱介电常数函数形式为εa(r)=kr2+b和b=10时三角晶格二维函数光子晶体TE模式和TM模式的带隙结构如图3所示, 其中k=3×1012, 介质柱半径r=0.4a.由图3可见, 当ωa/(2πc)=0～1时, TE波有5个带隙, TM波有2个带隙. 在频率为0.4附近, TE和TM波的带隙重合, 称为完全禁带. 在TE波带隙中有A和B两个点为类Dirac点.

图3 介质柱介电常数函数形式为εa(r)=kr2+b和b=10时三角晶格二维函数光子晶体的带隙结构Fig.3 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants εa(r)=kr2+b and b=10

由图1～图3可见, 随着折射率函数常数项b的增加, 在TE波中的带隙发生了蓝移, 均出现2个类Dirac点, 并在TM波的带隙中出现了新的禁带, 表明改变常数项b可实现函数光子晶体能隙结构的改变.

介质柱介电常数函数形式为εa(r)=kr2+b和b=9,k=5×1012时三角晶格二维函数光子晶体TE模式和TM模式的带隙结构如图4所示, 其中介质柱半径r=0.4a.由图4可见, 当增加函数系数k时, 在TM模式的带隙中出现了1个类Dirac点C, 两种模式的带隙均向低频率偏移.

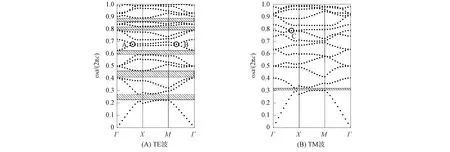
图4 介质柱介电常数函数形式为εa(r)=kr2+b和b=9, k=5×1012时三角晶格二维函数光子晶体的带隙结构Fig.4 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants εa(r)=kr2+b and b=9, k=5×1012

介质柱介电常数函数形式为ε(r)=k/(r+d)+b和r=0.2a时三角晶格二维函数光子晶体的带隙结构如图5所示, 其中k=7×10-6,d=2×10-6,b=11.由图5可见, 当ωa/(2πc)=0～1时, TE波有3个带隙, TM波有2个带隙, 当ωa/(2πc)=0.46～0.57时, TE和TM波的带隙中出现完全禁带.

图5 介质柱介电常数函数形式为ε(r)=k/(r+d)+b和r=0.2a时三角晶格二维函数光子晶体的带隙结构Fig.5 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants ε(r)=k/(r+d)+b and r=0.2a

介质柱介电常数函数形式为ε(r)=k/(r+d)+b和r=0.3a时三角晶格二维函数光子晶体的带隙结构如图6所示, 其中k=7×10-6,d=2×10-6,b=11.由图6可见, 随着介质柱半径r的增加, 在TE波带隙中出现一个带隙, TE波的带隙结构逐渐蓝移, 且完全禁带的宽度逐渐变窄.

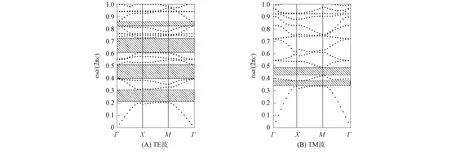
图6 介质柱介电常数函数形式为ε(r)=k/(r+d)+b和r=0.3a时三角晶格二维函数光子晶体的带隙结构Fig.6 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants ε(r)=k/(r+d)+b and r=0.3a

综上, 本文设计了一种二维函数型光子晶体, 并计算了TE和TM波的带隙结构. 结果表明： 在二维函数光子晶体中得到了绝对带隙和类Dirac点； 当介质柱半径和介电常数函数形式不同时, 带隙结构发生改变, 利用二维函数光子晶体可设计所需的带隙结构. 由于二维常规光子晶体的结构固定, 因此其带隙结构不变. 若需一种新的带隙结构, 则需对二维常规光子晶体进行改造. 对于二维函数光子晶体, 通过调节外部光强分布即可改变介质柱介电常数的函数形式, 同时调节介质柱的半径, 可改变函数光子晶体的带隙结构以及类Dirac点的位置.