一种增量式MinMax k-Means聚类算法

胡雅婷, 陈营华, 宝音巴特, 曲福恒, 李卓识

(1. 吉林农业大学 信息技术学院, 长春 130118； 2. 吉林省科学技术工作者服务中心, 长春 130021；3. 长春理工大学 计算机科学技术学院, 长春 130022)

聚类分析[1-4]是数据分析的一种基本方法, 既可作为一种无监督机器学习方法独立发现未标签数据结构, 完成数据分类、 压缩等工作, 也可与其他方法相结合以提高其性能.k-means算法是一种经典的划分聚类算法, 通过最小化类内方差之和获得硬聚类划分, 因其计算简单、 聚类效率高等优点广泛应用于模式识别、 机器学习、 图像处理及故障诊断等领域[5-8]. 但k-means聚类结果对初始聚类中心依赖较大, 导致算法易陷入局部极小值[9]. 为改善该问题, 可通过改进中心初始化方法降低初始化对算法的影响, 以获得目标函数的更优解[10-12].k-means++算法[13]通过随机选择程序实现初始化中心对整个数据空间的全覆盖, 在理论上保证了获得聚类划分可达到近似最优. 该类算法计算效率相对较高, 但对目标函数解的改善程度有待提高. 全局k-means聚类算法[14-17]作为一种增量式k-means聚类算法, 以每次迭代增加一个聚类中心的方式完成聚类数目的递增, 通过在数据中选择使目标函数值减少最多的数据点作为新增的聚类中心. 该算法明显提升了目标函数解的质量, 但计算效率较低.

针对上述改进算法存在的问题, Tzortzis等[18]提出了MinMaxk-means聚类算法. MinMaxk-means 算法以最小化最大的方差为聚类准则确定目标函数, 该准则能改善k-means算法迭代中产生过大方差类的问题, 从而得到目标函数更优的解. 由于直接优化最小化最大的方差准则函数对应一个非连续可微的优化问题, 因此MinMax算法通过优化加权k-means目标函数得到该问题的近似解. 与k-means及其初始化中心改进算法相比, MinMaxk-means算法能显著改善k-means算法目标函数解的质量, 计算效率比全局k-means及其改进算法更高. 但为了避免产生空类或单点类, MinMaxk-means算法采用自适应机制动态地调整参数p, 而参数p的合理取值区间为[0,1), 自适应调整不能保证其取值始终位于该区间内, 使算法存在产生空解的可能性.而且实验结果表明, 初始化中心对MinMaxk-means聚类结果影响较大, 初始化不当可导致迭代次数多、 迭代时间长、 目标函数解的质量差等问题. 为进一步改进MinMaxk-means算法性能, 受全局k-means增量式算法启发, 本文通过引入增量式聚类思想改进MinMaxk-means算法存在的上述问题. 对于给定的聚类数目k, 首先以较小的kmin值作为起始聚类数目, 通过对一个或多个聚类划分进行分裂, 以增加聚类数目直至达到指定的k值.与现有的增量式全局k-means算法每次迭代都需从数据集中筛选出新增的聚类中心不同, 本文算法通过分裂已有聚类划分完成增量式聚类, 并引入均衡化准则确定分裂对象, 其增量式过程计算效率更高, 同时能明显改善MinMaxk-means算法目标函数解的质量.

1 MinMax k-means聚类算法

MinMaxk-means聚类[18]是k-means聚类的一种改进算法, 通过改进k-means算法的目标函数改善其在迭代过程中易陷入局部最小值问题, MinMaxk-means的目标函数建立在最小化最大的类内方差准则上. 假设X是给定的数据集合,k是聚类数目, 则其目标函数为

(1)

其中V={v1,v2,…,vk}为聚类中心集合,Xi(1≤i≤k)为第i个聚类划分, 存储数据X中所有距离中心vi最近的数据点.目标函数等于X中所有距离中心vi最近的数据点与中心vi之间距离的平方和.

由于直接优化目标函数(1)对应一个非连续可微的优化问题, 无法直接利用迭代算法进行求解, 因此, Tzortzis等[18]对目标函数(1)进行了近似处理, 改写后的近似目标函数为

(2)

为了抑制某类方差之和的值过大, 式(2)将参数p的取值范围限定为区间[0,1).在迭代过程中, 为避免空类问题, 采用自适应策略更新迭代过程中的参数p, 设参数p的最大取值pmax并更新步长pstep, 参数p更新过程为

p=pmax-pstep.

(3)

(4)

MinMaxk-means聚类算法流程如下：

步骤1) 初始化参数pstep,pmax,β及聚类数目k、 迭代最大次数tmax和收敛精度δ；

步骤2) 初始化聚类中心V(0)；

步骤3) 利用V(0)与给定的参数, 优化目标函数(2)得到聚类中心V′[18]；

步骤4) 以V′作为k-means聚类的初始化中心, 运行k-means聚类算法直至收敛, 得到聚类中心V.

由于k-means与MinMaxk-means聚类算法的目标函数不同, 因此算法流程中前三步得到的聚类中心是最优化MinMaxk-means目标函数的结果. 而MinMaxk-means聚类的最终目标是优化k-means的目标函数, 因而在其最后一步需要运行k-means算法以获得优化k-means目标函数对应的最终聚类结果. 本文将完整的4个步骤称为“MinMaxk-means”聚类或者简称为“MinMax”聚类, 而文献[18]将前三步称为“MinMax”聚类, 将完整的四步称为“MinMax+k-means”聚类, 本质相同.

在MinMaxk-means算法的迭代过程中, 通过动态调整参数p处理空类与单点类问题. 但参数p的合理取值区间为[0,1), 自适应地调整不能保证其取值始终位于该区间内, 使得算法可能产生空解. 且通过实验发现, 初始化中心对MinMaxk-means聚类结果与效率均有较大影响, 初始化不当可导致迭代次数多、 迭代时间长的问题, 空解的产生也与算法初始化聚类中心的选择有关. 在UCI机器学习典型数据集Iris上分别运行MinMaxk-means和k-means算法. 图1为MinMaxk-means算法在不同聚类数目下的运行结果(算法参数设置与文献[18]一致, 运行50次取平均值). 由图1可见, MinMaxk-means算法存在如下问题： 1) 算法有空解产生, 且随着聚类数目的增加, 空解产生比例呈逐渐增大的趋势； 2) 算法并不能保证在给定的迭代次数内收敛. 图2为不同聚类数目下MinMaxk-means与k-means算法聚类迭代次数与运行时间的比值. 由图2可见, MinMaxk-means算法平均迭代次数明显高于k-means算法, 从而导致MinMaxk-means算法计算效率较低, 运行时间明显比k-means算法长.

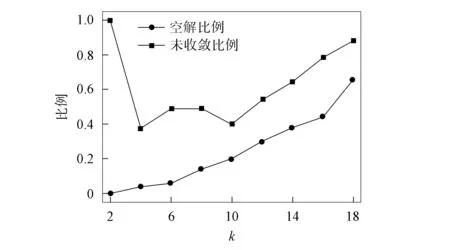
图1 MinMax k-means算法在不同 聚类数目下的运行结果Fig.1 Running results of MinMax k-means algorithms for different clustering numbers

图2 不同聚类数目下MinMax k-means 与k-means算法的比值Fig.2 Ratios of MinMax k-means and k-means algorithms for different clustering numbers

2 增量式MinMax k-means聚类算法设计

2.1 全局k-means算法

为避免k-means算法对初始化中心敏感的问题, Likas等[17]提出了一种全局k-means聚类算法, 该算法通过增量式增加聚类中心获取更优的目标函数解, 降低了k-means算法对初始化的依赖程度. 全局k-means算法流程如下：

步骤1) 初始化聚类数目k*=1, 初始化中心V为所有数据的均值；

步骤3) 以V′作为初始化中心, 运行k-means算法至收敛, 收敛后中心赋值给V；

步骤4) 如果k*=k, 则算法停止； 否则, 转步骤2).

全局k-means聚类算法降低了k-means算法对初始化的依赖程度, 但计算效率较低, 原因如下：

1) 在步骤2)中, 递增式增加一个中心, 全局k-means算法需要遍历所有数据点, 并选择其中对应的目标函数值最小的数据点作为下一个中心, 这一原则基于k-means算法的目标函数最小化; 增量式选择聚类中心时需计算各数据点之间的距离, 其计算量是O(N2s), 其中N为数据个数,s为数据维数, 而k-means每次迭代的计算量为O(Nsk).一般情况下k≪N, 使得全局k-means算法中心选择的计算量过大.

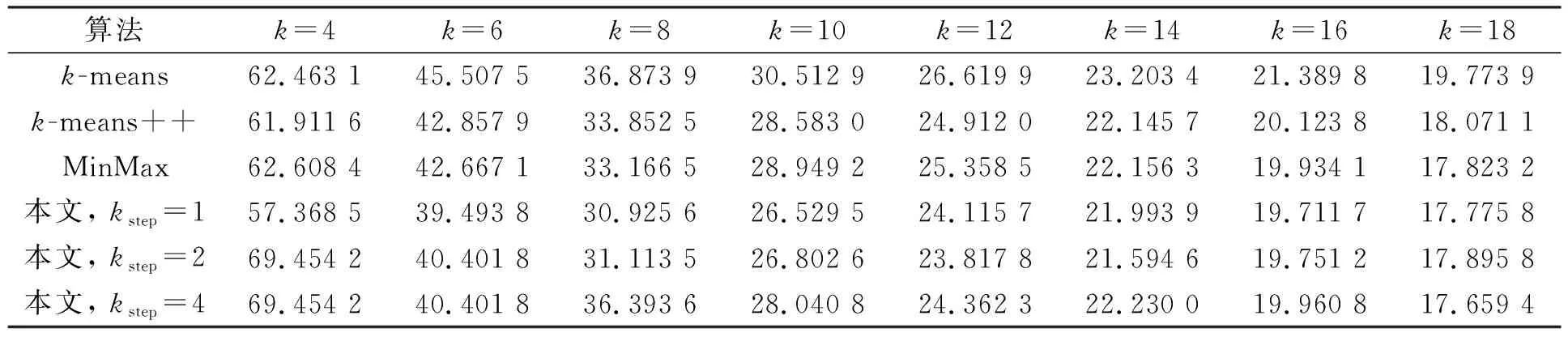
2) 在步骤3)中, 对每个单独的聚类数目k*(1

2.2 改进算法

本文采用全局k-means算法的增量式聚类思想降低MinMaxk-means算法对初始化敏感的问题. 尽管全局k-means算法的增量式聚类改善了聚类结果对初始化的敏感性, 但与原始k-means算法相比, 其增加了计算量, 计算效率非常低. 因此, 不能直接套用全局k-means算法的增量模式. 本文采用完全不同的增量式过程完成聚类数目的递增, 从而提升其计算效率.

针对全局k-means算法选择增量中心的过程计算量过大问题, 本文进行如下改进以提升其计算效率：

1) 针对已有的聚类划分进行操作, 并非针对数据点进行操作, 由于聚类划分数目远小于数据点的个数, 因此从遍历选择的角度具有优势；

2) 对每个划分采用分裂方式完成聚类数目的增加, 分裂可保证目标函数值是下降的, 这与优化k-means算法目标函数一致；

3) 借鉴MinMaxk-means算法的目标函数原则, 并在其基础上进行改进, 以快速确定被分裂的聚类划分.

MinMaxk-means聚类准则是最小化最大的类内方差, 以尽量保证各类内的方差均衡. 但对于不同聚类中数据数目不一致、 具有严重差异的问题, MinMaxk-means聚类准则并未考虑. 此时, 对数据数目过大的划分进行分裂可得到更均衡的类内方差结果. 本文采用各类数据均衡的思想确定被分裂的聚类划分, 避免不同聚类划分之间数据不平衡导致的类内方差差异过大问题, 从而降低算法整体目标函数值. 同时, 由此产生的计算量极低, 几乎可以忽略不计, 只需要记录各聚类划分的数据数目即可.

针对全局k-means算法时间复杂度较高的问题, 本文进行如下改进：

军功爵制是对五等爵制分封体制的一种继承，然而它却与五等爵制有着明显的差异和不同。五等爵制规定，天子、诸侯、大夫、士农工的世袭而定，“天子一位，公一位，侯一位，伯一位，子，男一位，凡五等也”[13]P782统治者内部等级和被统治着的身份地位也是受到五爵制的限定。“天子者，爵称也，爵所以称天下者何？王者父天母地，为天之子也。所以名之为公候者何？公者，通也，公正无私意也。侯者，候也，候逆顺也。伯者，白也。子者，孳也，孳孳无己也，男者，任也。”[14]P2而军功爵制则是春秋时期，诸侯根据当时的政治形势和社会环境对庶民做出的一种妥协。

1) 同时分裂多个划分, 一次性递增多个聚类中心以快速增加聚类数目, 从而不必对所有的聚类数目k*(1

2) 对每个增量过程中限制算法迭代次数不超过某个给定的较小值, 以降低计算量. 由实验结果可知, 降低迭代次数并不会影响该算法获取解的质量. 这是因为本文算法在迭代过程中采用了优化能力更强的MinMaxk-means迭代算法, 其优化能力优于全局k-means所采用的原始k-means聚类算法.

对于一个给定的数据集合X及给定的聚类个数k, 本文算法流程如下：

步骤1) 参数设定.设置最小聚类数目kmin、 聚类数目递增量kstep和最大迭代次数tmax；

步骤2) 计算初始聚类划分.令k*=kmin, 在保证迭代次数不超过tmax的前提下运行MinMaxk-means算法对数据集X进行聚类, 记录聚类结果中各聚类划分内部数据数目；

步骤3) 分裂聚类划分.

① 计算分裂聚类数目ksplit: 若kstep>k*, 则ksplit=k*, 否则,ksplit=kstep; 若k*+ksplit>k, 则令ksplit=k-k*；

② 确定被分裂的聚类划分: 对已有聚类划分按数据数目从大到小排序, 选取前ksplit个划分标记为待分裂划分, 其余聚类划分标记为稳定划分；

③ 确定新的初始化聚类中心Vinit: 令Vinit=Ø, 对每个待分裂划分, 从其数据集合中随机选取两个数据并入到Vinit； 对每个稳定划分直接选取其数据中心加入到Vinit；

④ 计算新聚类数目k*=k*+ksplit；

⑤ 根据初始中心Vinit、 聚类数目k*和最大迭代次数tmax, 运行MinMaxk-means算法得到新的聚类划分, 记录各聚类划分中的数据点个数；

⑥ 若k*

步骤4) 以上述步骤获取的k个聚类中心作为初始化中心, 运行k-means算法直至收敛, 得到最终的聚类结果, 算法结束.

3 实 验

3.1 实验环境与参数设置

为验证本文算法的有效性, 将其与k-means聚类及其改进算法进行比较, 对比算法包括原始k-means聚类算法、 MinMaxk-means聚类算法[18]和目前常用的中心初始化改进算法k-means++算法[13]. 实验数据集为UCI机器学习数据库中的典型数据集Iris(N=150,s=4)和Abalone_new(N=4 177,s=48), 其中N为数据个数,s为数据维数； 所有算法的最大迭代次数为1 000； MinMaxk-means算法中参数采用文献[18]中的推荐设置, 其中pmax=0.5,pstep=0.01,ε= 10-6,β=0.3.本文算法的参数设置为kmin=2, 增量聚类的最大迭代次数tmax=5.本文同时对比了kstep在不同取值下的聚类结果.实验结果取每种算法运行50次的平均值.实验代码以MATLAB编写, 硬件配置为CPU： Intel Core i3, 3.40 GHz; 内存12 GB.

3.2 实验结果与分析

3.2.1 与不同算法的对比结果

图3 不同数据集上MinMax k-means与 k-means算法运行时间的比值Fig.3 Ratios of running time of MinMax k-means and k-means algorithms on different data sets

图3为不同数据集上MinMaxk-means与k-means算法运行时间的比值. 由图3可见, 在不同数据集上MinMaxk-means和k-means算法的运行时间比值在10～90内变动. 图4为本文算法kstep取不同值时与k-means算法运行时间的比值. 由图4可见, 本文算法在参数kstep的不同取值下, 与k-means++算法运行时间的比值均小于7, 有些结果甚至快于k-means++算法. 因此, 本文算法的计算效率显著优于MinMaxk-means算法.

Iris和Abalone_new数据集上各对比算法的目标函数值分别列于表1和表2. 由表1和表2可见, 不同数据集、 不同聚类数目共计16组对比实验结果中, 其中15组实验结果本文算法优于MinMaxk-means算法, 占比达93.75%, 表明本文算法对MinMax的求解精度有明显优化效果. 以Abalone_new数据集在参数设为kstep=1的情况为例, 其函数值的6次优化结果百分数为0.6%～21%, 其他数据集与参数设置下的优化幅度也接近或高于该百分数. 在次于MinMaxk-means算法的一组实验数据上, 本文算法得到的仍是所有对比算法中的次优结果. 这里未列出空解产生的比例以及算法未收敛的比例. 对于所有实验数据集, 本文算法都能正常收敛, 并无空解产生, 表明本文算法可避免MinMaxk-means收敛速度慢、 易产生空解的问题. 对比实验结果表明, 无论在算法的运行时间上, 还是在目标函数值优化上, 本文算法均明显改善了MinMaxk-means算法存在的问题.

在时间效率上, 如图3和图4所示, 在k-means算法的不同改进算法中, 本文算法的计算效率最高, 其次是k-means++算法, MinMaxk-means算法的计算效率最低. 在聚类算法目标函数值上, 如表1和表2所示, 不同数据集、 不同聚类数目共计16组对比实验结果中, 本文算法15次取得了最优值, 12次取得了次优值, 明显优于其他3种对比算法.

图4 本文算法kstep取不同值时与k-means++算法运行时间的比值Fig.4 Ratios of running time of proposed algorithm and k-means++ algorithm when kstep takes different values

表1 Iris数据集上各对比算法的目标函数值

表2 Abalone_new数据集上各对比算法的目标函数值

3.2.2 参数kstep对本文算法的影响

kstep的取值对本文算法的寻优能力有一定影响.由表1和表2可见, 当k值较小(k<12),kstep取值为1,2时算法性能更好； 当k值较大(k≥16),kstep取值为4,8时算法性能更好.由图3和图4可见,kstep值越大, 本文算法的计算效率越高.这是因为随着kstep值的增加, 算法跳过的k值增多, 从而减少了迭代的总次数.

综上可见, 本文算法改善了MinMaxk-means算法易产生空解、 收敛速度慢和计算效率较低的问题, 并进一步提升了MinMaxk-means算法目标函数解的质量. 对比实验结果表明, 本文算法具有较高的计算效率, 得到的目标函数值明显优于其他对比算法.