一种改进型TF-IDF文本聚类方法

张 蕾, 姜 宇, 孙 莉

(1. 吉林大学 发展规划处, 长春 130012； 2. 吉林大学 计算机科学与技术学院, 长春 130012)

随着互联网技术的快速发展, 各种数据呈爆发性增长, 产生了大量文本信息, 因此采用文本分类技术对海量数据进行科学地组织和管理尤为重要. 机器学习技术对文本分类不需要人为干预, 因此被广泛应用[1-3]. 词频-逆文档频率(term frequency-inverse document frequency, TF-IDF)算法具有简单、 可靠性高等特征, 可用于对文本分类, 但也存在不足, 尤其是处理一些特定的分类问题(如学科交叉等问题)时, 存在对与文章内容关系不密切的生僻词给予过高权重的问题[4-5], 且TF-IDF算法未考虑词语在不同分类分布时对其权重的影响, 同一词语在不同论文分类中表示的意义和重要程度不同. 虽然LDA主题模型、 word2vec/doc2vec分布式模型和深度学习模型等经典方法在处理文本分类时都有其各自优势[6-7], 但在处理一些数据量较小无法满足深度学习算法, 也不能满足LDA主题模型、word2vec/doc2vec分布式模型时, TF-IDF算法可以解决这类问题. 因此, 本文采用TF-IDF向量空间模型作为词频向量转化模型. 传统TF-IDF算法在实际应用中当词项存在不同语义时在准确分析上还存在差距, 目前已有一些解决方法[8-9], 其中基于词频差异的特征选取方法被证明有效[10]. 本文提出一种基于改进TF-IDF文本聚类的分类方法, 以提高算法的准确性. 首先采用改进TF-IDF文本聚类方法进行词频向量提取； 然后利用K-mean++算法对TF-IDF算法生成的词频向量结果进行聚类分析; 最后利用词云方法和随机森林方法验证本文方法的有效性.

1 改进TF-IDF词频向量转化算法

1.1 TF-IDF算法

在文本分类中常用TF-IDF算法进行特征提取, TF-IDF算法是一种根据单词在语料库中出现频次判断其重要程度的统计方法, 主要思想是先对词频(term frequency, TF)进行统计, 认为词语出现次数越多, 则文档可能与该词语有越多的正向关联性, 再通过逆文档频率(inverse document frequency, IDF)减少常见词的权重, 计算公式为

TFIDFi,j=TFi,j×IDFi,j,

(1)

其中TFIDF表示词频TF和逆文档频率IDF的乘积, TFIDF值越大对当前文本的重要性越大.

本文使用的数据为离散化的关键词词条, 聚类算法无法直接计算关键词. 因此本文采用TF-IDF方法将关键词转化为词频向量, 聚类算法通过计算词频之间的距离计算样本之间的相似度.

1.2 改进TF-IDF算法

TF-IDF算法在本文应用场景中利用了特征词与其出现的文本数之间的关系, 而忽略了特征词在不同类别间的分布差异情形, 不利于提高分类的准确性. TF-IDF算法目前已有多种改进方法[11], 本文针对特征词在不同学科文献中出现的频率不同, 在不同学科中含义也不同的问题, 提出一种改进的TF-IDF算法, 利用现有学科分类作为参考, 区分特征词在不同学科中的含义, 以提高TF-IDF算法结果的置信度, 计算公式为

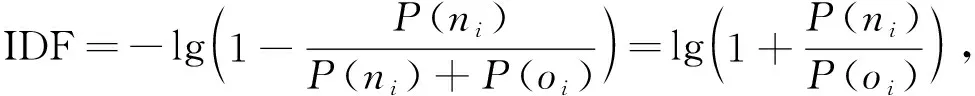
(2)

其中P(ni)表示特征词i在类n中出现的概率,P(oi)表示特征词i在文档中其他分类(文档中删除类n后所得分类)中出现的概率.在传统TF-IDF算法中, 两个特征词在文档中出现的次数相同, 但由于不同特征词的不同分布,P(ni)和P(oi)不同, IDF值也不同, 因此改进的TF-IDF算法可以更好区分不同特征词的分布情况.

算法流程如下, 其中算法的输入为论文文本集D, 输出为词频向量矩阵m.

算法1改进TF-IDF算法.

输入: 论文集D;

输出: 矩阵m;

初始化TF-IDF矩阵m;

在定义任务相关数据时，用户说明包含被挖掘数据的数据库和表(或者数据仓库和数据立方体)、选择数据和分组的条件、挖掘时要考虑的属性(或维)。这实际就是对多边矩阵本身框架的识别和认识，选取合适的框架定义多边矩阵的形式结构。

对论文j中的每个单词i, 循环执行以下过程：

计算单词i在该学科分类的频率P(ni);

计算单词i在其他学科分类的频率P(oi);

计算单词i在所有文献中的频率P(TF);

按

更新矩阵m中的每个值；

结束循环.

2 基于改进TF-IDF文本聚类的交叉学科分类方法

2.1 算法流程

本文实验方法及流程如图1所示. 首先利用WOS(Web of Science)数据平台进行论文索引, 选用数据库中索引的2015—2019年吉林省内各高校、 科研院所发表的所有论文信息, 利用改进TF-IDF算法对论文关键词进行词频向量转化处理, 形成文献的词向量矩阵; 然后利用K-means++算法对TF-IDF矩阵进行聚类分析； 最后采用随机森林算法[12]分别评估改进TF-IDF算法和传统TF-IDF算法的准确性.

图1 实验方法及流程Fig.1 Experimental method and process

2.2 K-means++算法

本文采用K-means++算法对TF-IDF算法生成的词频向量结果进行聚类分析.K-means算法是经典的聚类算法之一[13], 假设K-means算法的输入样本集为D={x1,x2,…,xm}, 聚类的簇数为k, 经过N次迭代后算法停止,K-means算法的运行步骤如下.

1) 从数据集D中随机选择k个样本作为初始的k个质心向量{c1,c2,…,ck};

2) 对于n=1,2,…,N, 进行如下操作：

① 将簇划分C初始化为Ct={ct}(t=1,2,…,k);

② 对于i=1,2…,m, 分别计算样本xi和各质心向量cj(j=1,2,…,k)的距离di,j=‖xi-cj‖, 将最小的xi标记为dij所对应的类别j, 然后更新Cj=Cj∪{xi};

④ 如果k个质心的位置都未发生变化, 则结束算法, 转步骤3);

3) 输出结果簇划分C={C1,C2,…,Ck}.

在K-means算法中, 质心位置的选择对最后的聚类结果和运行时间都有较大影响, 因此需选择合适的质心.K-means算法默认采用随机选择质心, 有可能导致算法收敛较慢, 时间开销较大[14].K-means++算法对K-means算法随机初始化质心的方法进行了优化.K-means++算法假设已经选取了n个初始聚类中心(0

3 实 验

3.1 数据集

本文实验的数据采用WOS数据库中的论文进行数据检索, 并按照ESI学科分类进行整理, 形成实验数据集. 实验数据集包含了2015—2019年吉林省全部科研机构发表以及合作发表论文的数据信息, 共筛选出53 346篇论文, 论文信息包含领域、 出版年、 被引频次、 学科领域百分位、 期刊影响因子、 关键词等, 并按基本科学指标数据库(essential science indicators, ESI)的22个学科领域进行分类, 包括计算机科学、 工程科学、 材料科学、 生物与生化、 环境/生态学、 微生物学、 分子生物与遗传学、 一般社会科学、 经济与商学、 化学、 地球科学、 数学、 物理学、 空间科学、 农业科学、 植物与动物科学、 临床医学、 免疫学、 神经科学与行为学、 药理学与毒物学、 精神病学/心理学、 多学科.

3.2 实验结果

图2 聚类8交叉学科词频分布Fig.2 Term frequency distribution of interdisciplinary in cluster 8

先分别利用传统TF-IDF算法和改进TF-IDF算法将论文关键词转换为词频向量矩阵； 然后用K-means++算法利用每篇论文关键词的词频向量进行聚类, 确定每篇论文所属的学科分类； 最后按ESI论文库标准的22种分类(ESI按论文所在出版刊物的所属学科进行划分), 与本文采用的单篇论文关键词聚类产生的结果进行学科交叉分析, 分析结果表明, 交叉学科对学科发展具有重要的指导作用[15-16]. 按轮廓系数标准确定K值, 当K=10时, 样本到同簇其他样本的平均距离最小, 聚类结果最好, 共产生10个聚类结果, 见表1. 本文以聚类词汇数量最集中的聚类8为例进行交叉学科群分析, 如图2所示.

表1 K-means++算法聚类结果

由表1可见： 聚类8形成的交叉学科群中化学学科类的关键词出现词频1 796次, 占化学学科关键词总词频的38.5%； 材料科学学科类的关键词出现词频847次, 占材料科学学科关键词总词频的33.8%； 物理学科类的关键词出现词频737次, 占物理学科关键词总词频的47.4%； 工程学科类的关键词出现词频782次, 占工程学科关键词总词频的57.1%. 聚类8中包括主要学科分类为化学、 材料科学、 物理学、 工程学交叉学科群, 该结果符合查询到的学科交叉规律[17].

图3 聚类交叉学科关键词分布Fig.3 Distribution of clustering interdisciplinary keywords

图3为聚类交叉学科关键词分布. 由图3可见, 聚类8中高频词汇也多为化学学科、 材料科学学科、 物理学科、 工程学科相关词汇, 如纳米颗粒(nanoparticles)、 合成(synthesis)、 碳(carbon)、 石墨烯(graphene)等, 说明在论文中出现的高频词汇也是学科交叉相对集中的科研热点.

随机森林算法是一种有效的分类预测方法, 分类精度较高[18], 本文用随机森林算法评估聚类结果的准确性. 随机森林算法包含16个随机树、 16个子集, 选取论文的学科分类、 发表年、 当前应用数量、 期刊名称、 影响因子、 学科百分数作为训练特征参数, 交叉学科分类作为目标参数. 用随机森林算法分别对传统TD-IDF算法与改进TD-IDF算法进行评估, 其精确率、 召回率、F1值和词频向量转化时间结果列于表2.

表2 传统TD-IDF算法与改进TD-IDF算法的评估结果

由表2可见, 改进TD-IDF算法能区分不同特征词在全部文档的分布情况, 提高了算法的精确率,F1值是综合评价精确率和召回率的指标, 虽然改进TD-IDF算法的召回率略有降低, 但改进TD-IDF算法的F1值更高, 表明改进TD-IDF算法在解决交叉学科聚类问题时具有的更高的置信度. 同时, 改进TD-IDF算法的词频向量转化时间略高于原始TD-IDF算法, 表明其在提高聚类置信度的同时, 并不会增加太多的时间开销.

综上所述, 本文提出了一种混合聚类的方法对WOS数据库中的论文信息进行分类, 分析了各学科间交叉研究的热点和发展趋势. 首先使用改进TF-IDF算法统计论文中的关键词词频, 然后采用K-means++算法进行聚类, 并对聚类结果进行词云分析, 最后通过随机森林算法评估改进TF-IDF算法和TF-IDF算法的准确性, 实验结果表明, 改进TF-IDF算法能更有效地解决交叉学科的分类任务, 从而为吉林大学双一流学科建设可持续发展提供决策依据.