基于改进蚁群算法的无人机集群任务分配和路径规划联合优化
2021-09-22苏梅梅程咏梅胡劲文赵春晖贾彩娟张剑锋
苏梅梅,程咏梅,胡劲文,赵春晖,贾彩娟,徐 钊,张剑锋
(1.西北工业大学,西安 710000;2.西安爱生技术集团公司,西安 710065)
1 引 言
随着无人机飞行环境日益复杂和无人机性能等要求的提高,无人机编队任务分配的安全性、资源分配均匀等需求也变得越来越高。之所以要进行任务分配,是因为多无人机在执行任务时,无人机的油耗等资源受限,无人机的突发故障以及无人机任务之间的优先级逻辑关系等都会影响无人机如何分配任务和执行任务。根据各种约束信息下得出任务规划指令,无人机才能在高保障、高效率、低消耗的需求下完成任务。目前,常用求解任务规划的算法主要有基于集中式的线性规划法、基于分布式市场机制的方法以及基于启发式的算法等。
基于线性规划的方法:该类方法主要通过建立满足需求的线性目标函数,2015年,Malvankar- Mehta[1]在复杂的有人/无人机器人任务分配系统,该团队针对有人/无人机器人任务分配问题,考虑各类风险因素以及人为因素的性能指标,利用非线性规划算法进行求解,完成无人机任务分配。2016年,Berger 等[2]针对异构飞行器静态目标搜索过程中的计算复杂度高的问题,提出了新的整数线性规划和二次规划公式,以降低计算复杂度和近似最优地解决包含异构智能体的离散静态搜索路径规划问题,在计算代价较小的情形下获得了包含异构飞行器的近似最优解。以同样思维处理异构机器人计算复杂度高问题的还有2017年Bays 等[3],他们解决了异构机器人团队服务代理运输过程中的任务分配问题。该过程是一个机器人根据任务的优先顺序,执行多个任务的过程。该方式可以保证得到解的存在性以及降低计算复杂度,然而通常用来解决单一的任务中,解决方案较单一化,不能处理需要多机器人协作才能完成的任务。另外,随着任务和机器人的增多,计算复杂度将呈指数级增长,这类方法的扩展性和效率较弱。
基于市场机制的方法:该类方法[4]通常基于分布式的框架,是解决多机器人任务分配(Multi Robot Task Allocation,MRTA)问题最流行的方法,如一级价格拍卖、动态角色分配、交易机器人、默多克、德马克夫、M+等。由于其良好的可扩展性,这些方法特别适用于分布式机器人领域。在这些方法中,每个分布式代理都会计算一个完成任务的费用,并广播该任务的出价。拍卖机器人会决定最佳出价,而中标者会尝试执行中标的任务。它们有效地满足了机器人的实际需求团队,同时通过捕获分布式和分布式服务器各自的优势来产生有效的解决方案。但是,在任务分配过程中,如果通信成本太高,机器人的沟通性能会明显下降[5],因此这些方法适用于中小规模的任务分配。2018年,Bays 等[6]针对异构结构的空间约束的优先约束问题,提出了一种带有调度约束的分布式任务分配拍卖法,比使用整数线性规划解决此类问题提高了计算效率。同样,2011年,Chen等[7]研究了考虑资源约束的一组异构移动机器人的多机器人任务分配问题。机器人按照任务执行所需要的资源来划分。由于每个机器人可能没有足够的资源单独完成分配的任务,因此在任务执行中,机器人必须组成联盟,以满足任务强加的资源约束。
基于启发式算法:与上述两种算法不同,启发式算法[8]在处理任务规划问题时,由于其本身的随机性不再是试图搜索全局空间,而是在计算时间和最优性能之间达到某些妥协,使得同时兼顾计算效率和性能之间平衡的一个次优解。2013年,Yuan 等[9]为了解决多机器人系统的任务分配问题,提出了一种基于爆炸进化的免疫遗传算法。Manathara 等[10]针对多无人机作战的最优资源分配问题,针对多种异构无人机设计了任务分配策略,并采用启发式算法进行求解。Marden等[11]针对多智能体系统中的分布式控制问题,考虑了分配效能函数设计问题,并分析了效能函数同纳什平衡之间的关系。2013年,该团队针对多类资源分配问题,采用改进的基于状态的博弈论方法,进一步优化了效能函数,相比传统的博弈论,提高了资源分配求解速度。2014年,Nagarajan等[12]通过最大限度地提高通信效率和处理成本,提出了一种适用于异构多机器人系统任务处理的启发式搜索任务分配算法。针对任务数量大于系统中机器人数量的给定问题,采用对等结构算法找到近似最优分配方案。且其研究了多机器人系统的任务分配过程,为了解决多机器人系统的最优任务分配问题,针对动态环境下多机器人系统的自主任务分配问题,采用了一种改进的蚁群算法,考虑了任务约束和机器人能力。在所有情况下,蚁群算法都比IG 启发式算法得到了更好的结果。2014年,美国珀杜大学Kim 等[13]针对异构无人机的编队区域搜索和任务分配问题,提出了一种基于响应阈值模型的概率决策机制的分布式方法,考虑了环境的不确定性,实现了快速灵活的无人机区域搜索和任务分配。2019年,Zhao 等[14]利用强化学习算法Q-Learning 进行快速任务分配,利用神经网络近似和经验优先重放,将在线计算转移到离线学习过程中,具体就是开发了一个Q 网络编码分配规则,有效地将各种不同的任务分配给无人机。采取同样方式的还有2019年Dai 等[15]为了解决环境探测中的多无人机协同搜索问题,通过采用基于拍卖方法、空缺链方法、基于策略选择的Q-Learning 方法来求解多任务动态勘察与破坏的问题。不同的是,该篇文章考虑的目标具有反打击能力,从而增加了问题的复杂性。2020年,Brown 等[16]研究了具有任务间优先约束的应用中大型机器人团队的顺序任务分配和无碰撞路由问题,提出了一个层次算法来计算问题的最优解。2020年,Gibson 等[17]利用A*算法实现了实时的多智能体路径规划算法。本文通过建立约束下的无人机模型,每个无人机的模型将在每个时间步骤中更新,并确定最终的控制。生成的路径以路径点序列的形式提供给无人机。2018年,Zhou 等[18]以固定翼无人机辅助MCS 系统为研究对象,从能效的角度研究了相应的联合路径规划和任务分配问题。将求解的联合优化问题转化为双边两阶段匹配问题,第一阶段采用动态规划或遗传算法求解路径规划问题,第二阶段采用Gale Shapley算法求解任务分配问题。然而,2019年,Hafez等[19]研究了无人机协同任务分配和协同飞行轨迹规划问题,提出了一种新的层次模糊控制器和粒编队算法。2019年,唐俊林等[20]基于合作型协同进化算法的理念,提出了一种基于竞争型协同进化的多传感器任务规划算法。首先,建立了防空多传感器任务规划数学模型;其次,基于竞争型协同算法建立框架,并设计了新的编码方式,提出了交叉、变异以及冲突消解的策略。2020年,史人赫等[21]综合考虑速度增量和变轨时间等指标,基于双脉冲霍曼转移构建了一种两层任务规划框架。在此基础上,提出了一种新型网格编码差分进化方法。该方法引入序列逐次枚举思想,快速生成满足一对一任务约束的任务指派矩阵,并定制一种面向离散网格编码的差分变异操作,在保证任务规划方案可行性的前提下实现设计空间的高效探索,从而有效求解在轨服务任务规划问题。
另外,还有一些学者采用其他方式实现任务分配的目的。例如,2019年,于晓强等[22]针对大型空间结构的在轨装配任务分配问题,提出了基于扩展一致性算法的拍卖算法,在考虑在轨装配过程中运输、安装等任务的时间先后特性以及某些特定复杂任务需要多航天器协同完成的任务约束条件下,解决将各项任务分配给多个多种类航天器的在轨装配任务分配问题。2019年,朱利等[23]为了在最短时间内降低整个区域的环境不确定度,提高多无人机协同区域搜索效率,提出了一种基于Voronoi 图质心的多无人机协同区域搜索算法。针对不断变化的环境信息,提出了Discrete Combined Partition and Search(DCPS)策略,该策略将Voronoi 图质心用于引导无人机运动,任务区域在每一步搜索时都会被重新进行Voronoi 图划分。2021年,杜越洋等[24]针对无人机载荷选型以及载荷试验过程复杂、试验周期长、试验成本高的问题,设计了一种基于数据分发服务通信技术的无人机任务载荷综合仿真平台。
上文提到的方法都是先进行任务分配,然后将任务分配的结果输入到路径规划模块生成所需要的路径。未考虑任务分配和路径规划的耦合性。然而这一种处理方式在进行任务分配时未考虑无人机本身的运动学约束,仅考虑任务之间的关系,路径规划的输入是任务分配的结果,降低了问题求解的复杂度,但在实际任务中无法满足需求。为了应对以上困惑,很多学者将任务分配与路径规划耦合求解。2015年,Kim 等[25]针对无人机团队在不同目标移动的环境中执行搜索和破坏任务,在此背景下作者将搜索计划和任务分配在一个框架下进行建模,提出了一种基于响应阈值模型的概率决策机制的分布式方法,搜索计划为每架无人机生成一个有效的搜索路径,以方便快速地进行目标检测。Deng 等[26]在考虑了UAV 的弹药数量约束条件下,通过改变遗传算法的基因编码方式,完成了问题的求解。以上文献均是基于集中式架构完成协同任务规划问题的建模与求解,将规划运算过程完全在地面站或某个UAV 上完成。2017年,崔乃刚等[27]以多异构无人机执行侦察、打击以及评估任务为场景,利用分布式规划框架和图论思想对问题进行建模,在考虑了避碰、燃油和任务次序约束条件下,采取遗传算法进行任务规划问题的求解。然而其规划出来的路径存在交叉现象,会增加无人机间的防撞可能性。2019年,Albani 等[28]在多机器人的工作区域中利用分层任务分配与路径规划寻找框架,该框架扩展了仿生多机器人任务分配(MRTA)框架,使用Floyd-Warshall 算法将任务分配问题与路径规划问题耦合求解。该框架主要包括三个步骤,分别是把每个机器人通过感知获得可用的局部知识,以及与其他机器人交互的任务分配,利用其他机器人的知识制定运动规划。
综上所述,启发式算法在耗时和解的最优性能之间进行综合考虑,使得同时兼顾计算效率和和性能之间平衡的一个次优解。其中,蚁群算法由于其分布式求解的方式,在解决多任务场景问题中受到广泛的使用。另外,为了更符合实际应用的需求,将任务分配与路径规划耦合求解是必不可少的。最重要的是,大部分学者在无人机任务规划过程中都考虑了任务的约束和时间的约束,在规划时往往会出现无人机没有被分配到任务,原因是在规划的过程当中没有考虑将所拥有无人机资源进行充分利用的约束条件。
本文主要解决复杂多任务多编队场景中,在考虑任务优先级、航路最短以及耗时最短等约束,建立任务分配和路径规划的联合优化模型,采用改进的蚁群算法实现任务规划。其中,改进的蚁群算法主要是为了避免在任务分配过程当中出现路径交叉、资源分配不均匀的问题。为了解决该问题,本文主要通过引入执行任务的编队数量的约束,且改进信息素更新机制来实现。
2 问题描述
2.1 任务分配和路径规划联合优化模型
任务分配是运筹学中基本的组合优化问题。多无人机任务分配是指在给定无人机种类和数量前提下,充分考虑战场环境、任务要求和载荷能力约束,研究如何将合适的任务在合适的时间分配给合适的无人机。典型的任务分配模型有基于旅行商(Travelling Salesman Problem,TSP)模型、混合整数线性规划(Mixed-Integer Linear Programming, MILP)模型、车辆路径问题(Vehicle Routing Problem, VRP)模型、指派问题模型及运输问题模型。上述模型通常用于单智能体场景中。随着信息技术的发展,无人机的能力和应用领域越来越广泛。为了完成一项复杂的任务,需要多无人机合作和协调。复杂环境下的多无人机系统的协作与分配是研究热点问题。
本文旨在解决复杂环境中,大型固定翼无人机投放小型固定翼无人机群,在经过巡航阶段后,抵近目标区域,进行地毯式搜索侦察、干扰等任务。在整个过程中,无人机编队的任务规划包括任务规划和分配、航路规划。本文研究的是多无人机编队多类型任务分配问题以及航迹规划问题,由大型无人机携带小型无人机群飞往任务执行区,首先通过大飞机抛撒小型无人机群,再通过任务分配指令将小无人机群分成多个任务组进行巡航至任务地点,以不同的任务队形执行任务。每个无人机编队由一个无人机做长机,多个无人机做僚机来实现队形的控制。任务分配准则是整体工作效益最大化、耗时最小化。下面将对含约束情况下的任务分配模型建立展开详细的介绍。本文的任务规划场景示意图如图1 所示。
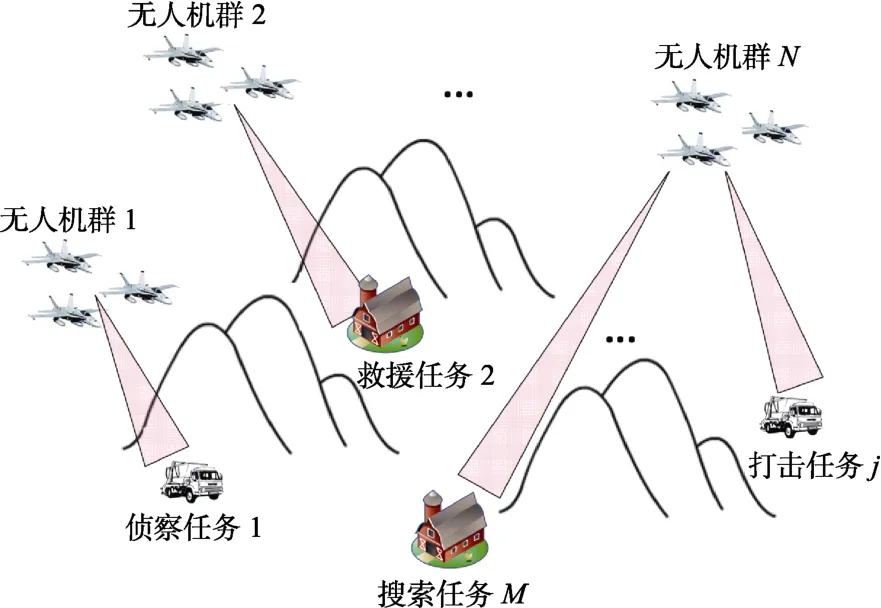
图1 多任务多编队任务规划的示意图Fig.1 Multi-task multi-subgroup task planning
如上述任务场景所示,假设有N个无人机编队组成的固定翼无人机集群集合U=[U1,U2,…,UN],K个任务的集合M=[M1,M2,…,MK],每个固定翼无人机编队均可执行任意任务,每个任务需要的编队数量小于等于1,不同的任务需要无人机编队用不同的队形去完成。例如,侦察任务需要使用“一字队形”才能保证侦察范围的覆盖率。而突防攻击任务需要使用“三角队形”才能保证前方无人机攻击后方无人机掩护的安全性。
与传统任务分配建模不同,本文的固定翼无人机编队在选择执行任务时,会同时兼顾任务的优先级顺序和距离约束进行选择。具体是指,每个固定翼无人机编队在选择任务区域时根据自己的队形优先选择与自己相对应的任务区域,因而每个编队都有自己对应的优先级准则,当排在优先级最前面的任务完成时,再去变换队形完成下一个优先级的任务。要求当任务分配结束后,必须保证所有任务均被执行。因此,对于编队U1来讲,其执行任务的优先级是M1,M2,…,MK,对编队U2来讲, 其执行任务的优先级是M2,M3, …,M K,M1,对于编队Un来讲,其执行任务的优先级是MK,…,M2,M1。另外,通过设计任务评价矩阵来判断该无人机是否已经执行任务,如果无人机已经执行任务,则该无人机的任务评价矩阵为零。本文的目标是将K个任务分配给N个无人机编队,使得在能耗和时间消耗最少的情况下总体收益最大。综上所述,本文设计如下的任务和路径规划模型。
假设:(1)UAV 的燃油限制约束可以等价于UAV 的最长飞行时间;(2)无人机可以正常通信,不受通信干扰,甚至通信中断;(3)UAV 在任务期间不会被破坏。
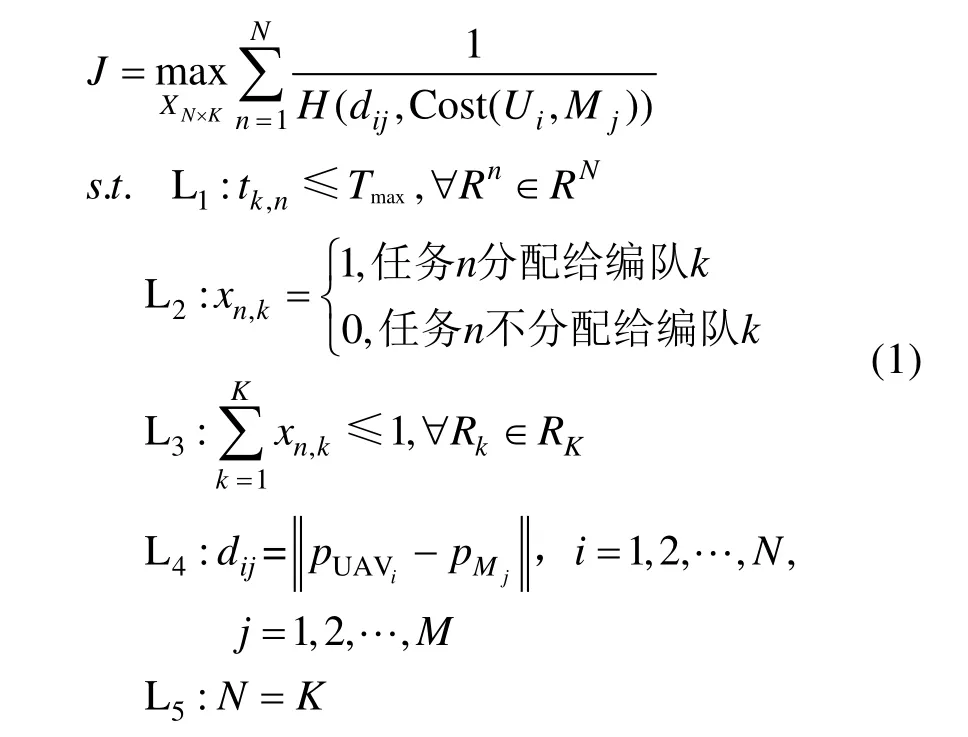
其中,J函数为本文的优化指标;为本文的任务分配和路径规划的综合代价;1L 代表时间的约束;2L 代表任务分配到无人机的值;3L 代表一个任务仅需要一个编队来完成。通常,任务规划是在上述约束条件下进行任务分配。
不同于传统的建模方式,本文为了充分利用所有的编队资源,使得任务完成的时间消耗最少,并兼顾执行任务的优先级别和路径最优的原则。设置了约束条件L4和L5,pUAVi代表i号编队的位置,Mpj代表j号任务的位置。L4代表每个无人机编队在选择任务时仍要考虑就近原则,即假设对于任务M1来讲,编队U1和编队U2均搜索到任务M1,按照任务优先级,此时应该编队U1去执行M1,然而此时编队U2距离M1更近,且若编队U1去执行M1可能会与其他编队的路径出现交叉,会增大编队之间的碰撞的可能性。因此,本文将会安排编队U2去执行M1,编队U1去执行其他任务。L5条件是指执行任务的编队数量和所拥有的编队总数量相等,该约束避免了出现无人机没有被分配到任务的情况。
2.2 无人机集群编队ID 设计
在进行无人机多编队任务分配和路径规划之前,本文首先将散乱的无人机群通过调用ID 的方式实现各编队的集结。ID 表示包括编队编号和各编队各无人机的编号。然而,在编程过程中考虑到变量名的第一个字符不能是数字,所以本文将采用UAV+ID 作为这架飞机的名字。
(1)方法1:十进制数表示法
由于本文的无人机数量为30 架,因此本文通过三位十进制数来设计ID 编号,如图2 所示,其中,百分位的十进制数代表无人机编队的编号,十分位和个位的十进制数的组合代表编队中各无人机的编号。因此,利用十进制数设计的无人机ID 的格式为UAV101,UAV315 等。其分别代表1 号编队中的1 号无人机,3 号编队中的15 号无人机。
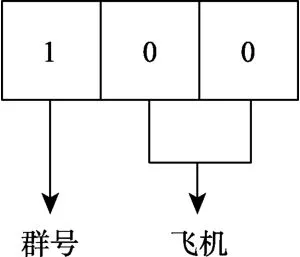
图2 基于十进制编队ID 的设计Fig.2 Design of formation ID based on decimal
(2)方法2:二进制数表示法
另外一种设计无人机ID 的方式是采用二进制的方式。与方法1 类似,编队ID 的设计包含编队编号和编队中各无人机的编号,总共包含8位,前四位是指无人机编队的编号,后四位是指编队中各无人机的编号。如图3 所示,例如,00010010 和00100011 则分别代表1 号编队中的2号无人机和2 号编队中的3 号无人机。
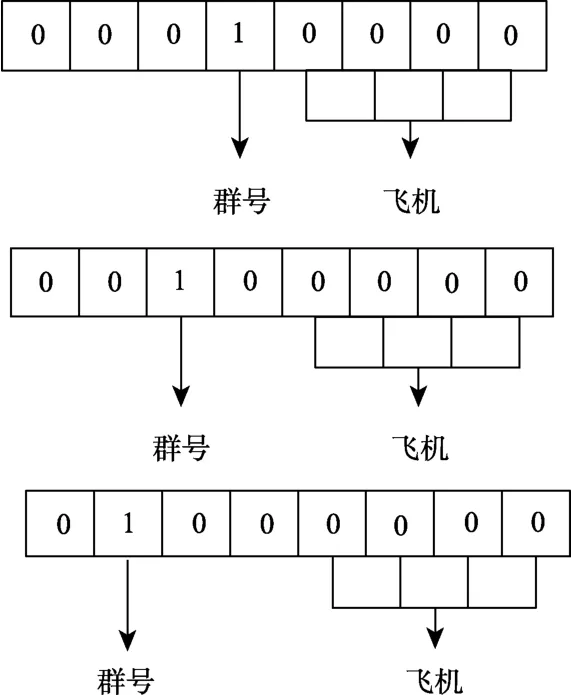
图3 基于二进制编队ID 的设计Fig.3 Design of formation ID based on binary
通过对比分析,为了更加清晰易懂地识别编队编号,本文选用方法1 来设计各无人机的ID编号。由于本文在集中式框架下进行编队,在分配任务时,将各编队视为整体。
3 基于改进的蚁群算法的任务分配和路径规划
与传统的蚁群算法不同的是,本文将任务分配和路径规划耦合讨论。由2.1 节建模分析可知,多无人机多任务规划问题是一个典型的组合优化问题,且在文献[29-30]中已经证明了该问题是一个NP-hard 问题,因此其求解难度很大。正如研究现状分析可知,为了降低求解难度,通常任务分配与路径规划可分为两个子问题来求解,路径规划的输入是任务分配的任务序列,弱化其两者之间的耦合性。然而,这种处理方式往往不考虑模型自身的运动学约束、任务之间的相互影响,以及任务分配取决于路径长度,只有根据分配策略才能获得准确的路径长度等因素。因此,任务分配与路径规划问题必须耦合[31]分析才满足实际要求。
另外,为了考虑任务优先级顺序和充分利用无人机编队资源的约束,本文设计新的信息素更新机制。传统的蚁群算法信息素更新机制,对于蚂蚁来讲,每个任务对应的Q 是在同样的条件下进行更新的。即在同样的信息素浓度增强系数的影响下,蚂蚁搜索任务时不会考虑任务的优先级顺序。然而,这种更新机制在本文的任务背景下会导致无人机编队在执行任务时有可能存在队形不断切换的问题,增加了问题的复杂性。
为了解决上述问题,本文在使用蚁群算法求解多任务分配问题时,将本文所期望的整体收益函数模块加入到概率更新公式中,使得蚁群在搜索的过程中有着更多的启发信息。更有针对性地找到满足本文需求的目标,改善了传统蚁群算法的随机性和解的最优性。为了使得无人机编队在搜索寻找任务时能够兼顾任务的优先级约束,保证无人机在任务分配过程中,能够充分利用资源,使得总体工作时间尽可能较少,本文通过把任务优先级因素考虑到信息素更新机制中。具体是指,通过对无人机编队和任务进行编号,相应的编队对应的与其队形相符合的任务。蚂蚁在搜索任务时,如果无人机编队编号与任务编号对应,则其留下的信息素浓度将会更多,反之,当无人机编队搜索到的任务编号不对应时,其留下的信息素浓度会较少。信息素增强度系数Q的设置如下。
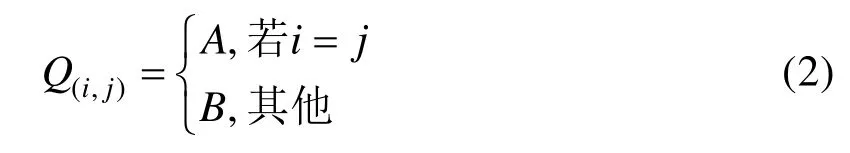
同时,本文在进行任务分配的同时,兼顾路径规划的实际情况。首先,将任务随机分配给某个节点处。然后根据当前蚂蚁编号,临界点矩阵采取不同的分配策略的蚂蚁编号的临界点。其中蚂蚁在公式(2)信息素增强因子启示下,散布信息素浓度,更新信息素浓度。蚂蚁根据信息素规则,每个任务分配好无人机编队后,本文同时进行路径规划的求解,在任务分配过程中,无人机获得无人机任务序列后,路径规划过程为每个无人机生成可飞行安全的路径,以最小化/最大化预定义的目标函数,如寻求最短的飞行路径。
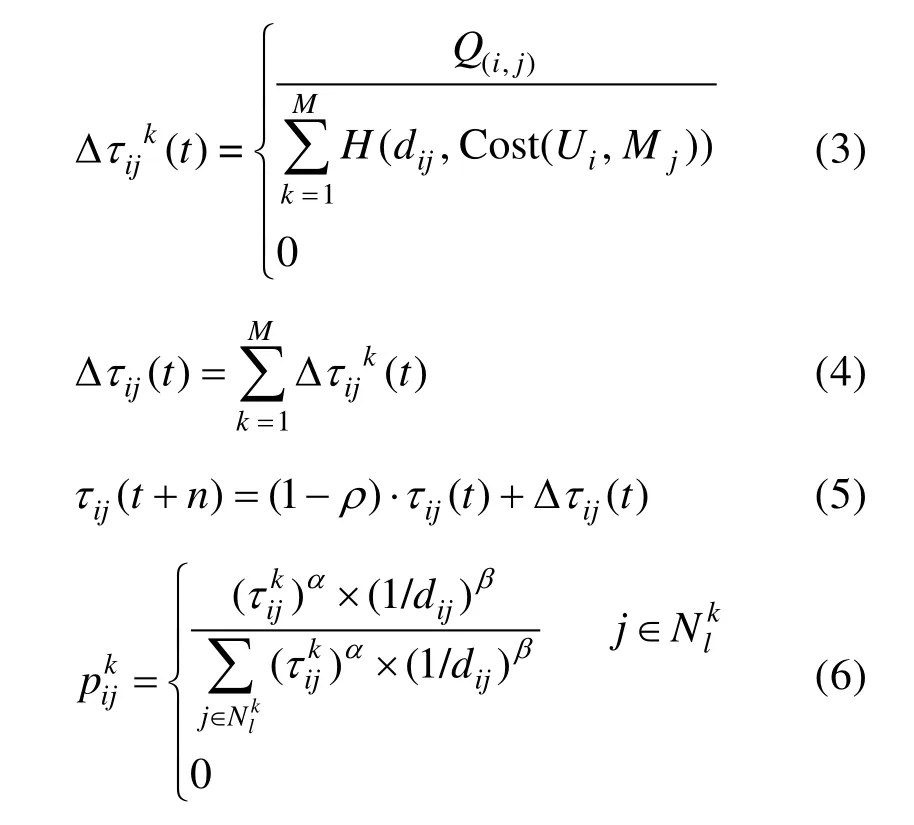
其中,τij(t)为t时刻节点i与节点j之间的信息素浓度;ρ为信息挥发因子;α为信息启发因子;β为期望启发式因子;H(dij,Cost(U i,Mj))为固定翼无人机编队任务分配和路径规划的综合代价;Cost(U i,Mj)为蚁群根据任务执行难易程度选择任务i的代价;dij为无人机编队与任务之间的距离。本文所提算法的流程图如图4 所示。

图4 改进的蚁群算法的流程图Fi g.4 Flow chart of improved ACO
本文所提算法的运算复杂度分析如下:假设每个编队需要执行n个任务,采用改进的蚁群算法的求解运算时间复杂度为O(n4);空间复杂度O(n2)。根据编程过程当中循环迭代机制,其中n是任务数量,m是蚂蚁数量,T是迭代次数,m通常取n的2/3,记m=2n/3;T通常取n的倍数,记T=k·n,则时间复杂度2n(n–1)nTnk/3,当n趋于无穷大时,k会远小于n,故时间复杂度为O(n4)。空间复杂度n·n+n·m,当n趋于无穷大时,空间复杂度约等于n2,故空间复杂度为O(n2)。
4 仿真结果及分析
本文在MATLAB2019b 平台进行仿真验证,将进行多组仿真实验验证本文算法。本文将通过性能指标来分析算法的有效性。为了充分验证本文所提出算法的正确性,设置了三种情形,分别是编队个数小于任务个数、编队个数等于任务个数以及编队个数大于任务个数。并分别采用传统的蚁群算法和本文提出的改进的蚁群算法进行对比,充分展示本文保证资源充分利用以及距离约束条件下的任务规划结果。
4.1 性能指标
为了评价本文算法的有效性,本文设置以下性能指标。
(1)任务完成数量等于K;
(2)执行任务的无人机编队量等于N;
(3)每个编队路径的重合度为0;
(4)资源分配不均匀度(无人机闲置个数)为Y。
4.2 仿真任务场景设置
在实验的过程中,蚁群的数量很重要,因为蚁群数量过大,会导致搜索过的路径上信息素变化趋于平均,这样就不好找出好的路径了;蚁群数量过小时,易使未被搜索到的路径信息素减小到0,这样可能会出现早熟,没找到全局最优解。通常,在时间等资源条件紧迫的情况下,蚂蚁数设定为城市数的1.5 倍较稳妥。本文主要设置了三种任务,分别是抵近侦察、协同干扰和电子对抗。
为了进一步说明本文所提算法的有效性,将分别讨论无人机编队个数和任务个数相等和不等的情形下进行仿真验证。在仿真环境中本文设置了最多五个无人机编队和最多五个任务,并根据优先级顺序依次注明无人机编队标识和任务标识,分别是{U1,U2,U3,U4,U5}和{M1,M2,M3,M4,M5}。通过多次测试,参数A=200、B=50效果最为满意,根据本文的三种任务场景的难易程度,本文设置Cost(U i,Mj)矩阵如下:
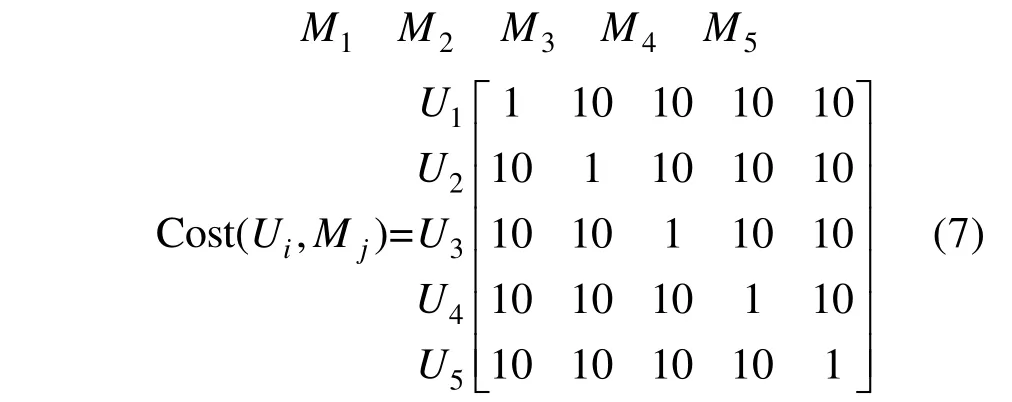
4.3 多任务多编队任务规划仿真验证与分析
本文的子群集结仿真结果如图5 所示,蓝色的“■”代表无人机的起始位置,红色的“▲”代表无人机的目标位置。红色的轨迹代表Leader 的飞行轨迹,其余黑色轨迹代表Follower 的飞行 轨迹。在不碰撞的前提下,30 架任意初始位置的无人机通过对ID 的调用,使用集结控制算法,经过400s 后,实现了三个子群的分群。每个子群集结成各自所指定的队形,分别为一字形、三角形以及圆周队形。
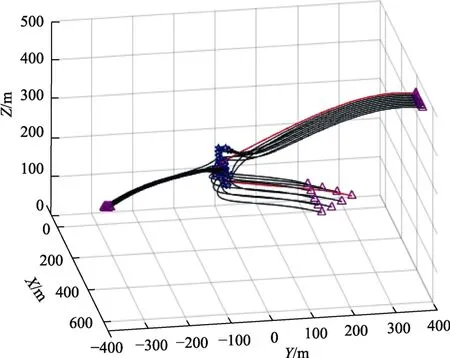
图5 基于ID 的无人机编队集结仿真图Fig.5 UAV subgroup aggregation based ID
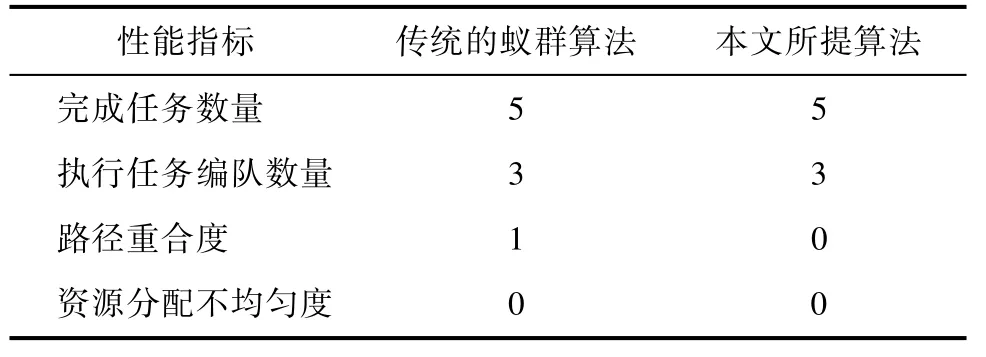
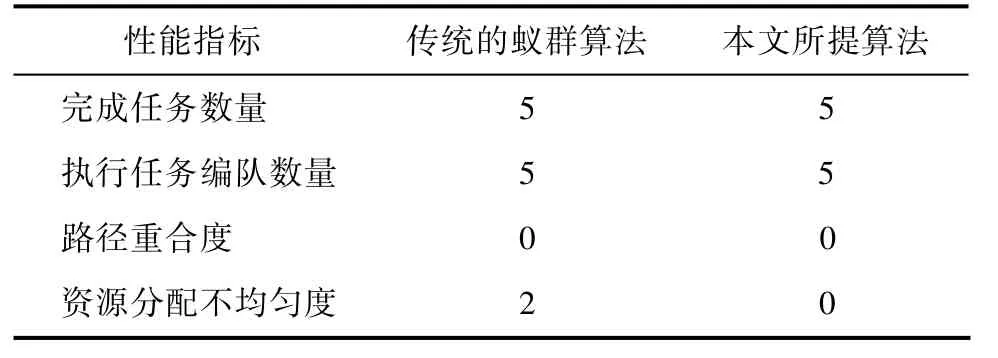
情形1:编队个数小于任务个数(N 根据图6(a)可知,当编队个数小于任务个数时,利用蚁群算法求解任务规划问题时,存在两个无人机编队路径交叉的现象。通过本文所提出的启发式蚁群算法,当编队个数小于任务个数时,充分利用了每个无人机编队资源,并且在兼顾距离约束和编队执行任务的优先顺序约束的条件下,满足本文任务分配和路径规划的性能指标,分配结果如图6(b)所示。表1 对比说明了本文所提算法路径重合度优于传统的蚁群算法,即防撞性能更优。 图6 传统的和改进的蚁群任务分配与路径规划仿真图(N < K)Fig.6 Traditional and improved ACO task assignment and path planning(N < K) 表1 多任务多编队任务分配和路径 规划指标(情形1)Table 1 Index of multi-task, multi-subgroup task allocation and path planning (case 1) 情形2:编队个数等于任务个数(N=K) 根据图7(a)可知,当编队个数等于任务个数时,利用蚁群算法求解任务规划问题时,同样存在两个无人机编队“空闲”的现象。通过本文所提出的启发式蚁群算法,当编队个数等于任务个数时,充分利用每个无人机编队资源,并且在兼顾距离约束和编队执行任务的优先顺序约束的条件下,满足本文任务分配和路径规划的性能指标,分配结果如图7(b)所示。表2 说明本文所提算法在该场景中资源分配更加均匀,不存在无人机空闲的情形。 图7 传统的和改进的蚁群任务分配与路径规划仿真图(N = K)Fig.7 Traditional and improved ACO task assignment and path planning(N = K) 表2 多任务多编队任务分配和路径 规划指标(情形2)Table 2 Index of multi-task, multi-subgroup task allocation and path planning (case 2) 情况3:编队个数大于任务个数(N>K) 根据图8(a)可知,当编队个数大于任务个数时,利用蚁群算法求解任务规划问题时,同样存在三个无人机编队“空闲”的现象。经过本文所提出的启发式蚁群算法,当编队个数大于任务个数时,由于每个任务仅需要一个编队执行,所以仍然存在两个编队闲置,但与传统的蚁群算法相比,本文所提算法充分利用了每个无人机编队资源,并且在兼顾距离约束和编队执行任务的优先顺序约束的条件下,满足本文任务分配和路径规划的性能指标,分配结果如图8(b)所示。同时,表3 表明在该场景中本文所提算法的分配均匀度优于传统的蚁群算法。 表3 多任务多编队任务分配和路径规划指标(情形3) Table 3 Index of multi-task, multi-subgroup task allocation and path planning (case 3) 图8 传统的和改进的蚁群任务分配与路径规划仿真图(N > K)Fig.8 Traditional and improved ACO task assignment and path planning(N > K) 本文主要解决了多任务多编队的任务分配和路径规划问题。通过对现有的任务分配算法进行调研发现,蚁群算法是解决多编队多任务分配和路径规划有效的解决算法,在保证较优解的同时计算效率也可满足需求。同时,指出了任务分配和路径规划过程中没能充分利用资源,使得出现无人机“空闲”的问题,以及路径交叉问题。针对上述问题,本文通过分析多任务多编队的任务分配和路径规划的实际需求,在考虑距离、时间以及任务优先级等约束基础上,建立了任务分配和路径规划耦合的优化模型,且提出了启发式的蚁群算法。最后,通过仿真验证本文算法与传统蚁群算法的效果对比,证明了本文算法的有效性。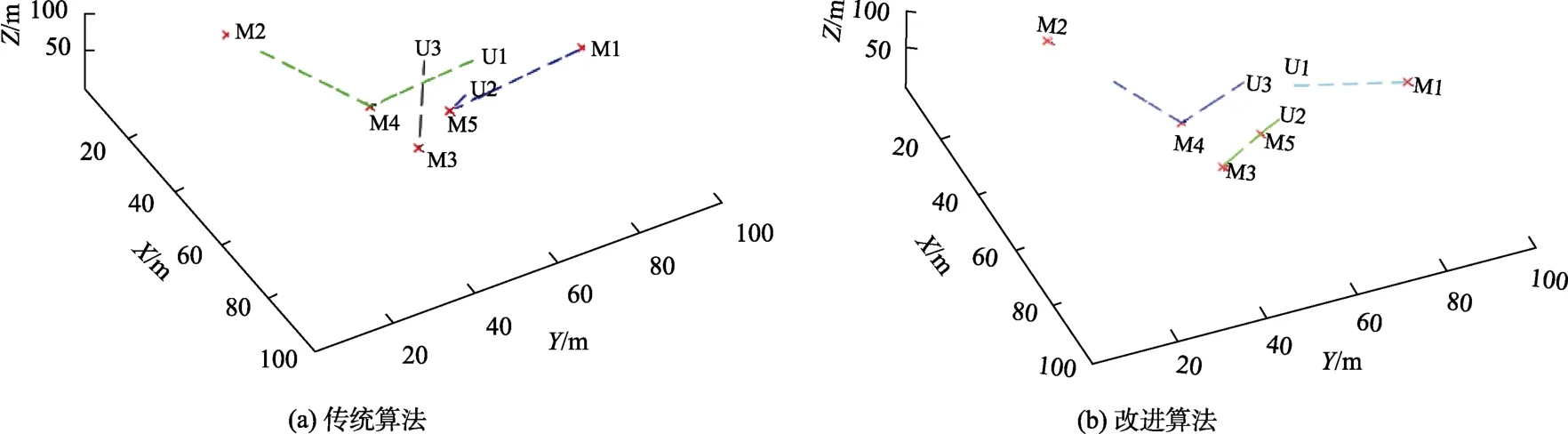


5 结 论
