基于反比佣金率约束的第一价格和第二价格拍卖模型
2021-09-22赵凤荣
赵凤荣,邬 俊
(1.昆明理工大学 a.管理与经济学院; b.国际学院,昆明 650093;2.内蒙古师范大学 计算机科学技术学院,呼和浩特 010022)
提要:通过假定反比佣金率的具体形式,采用贝叶斯-纳什均衡分析,分别得出带有保留价的第一价格和第二价格密封式拍卖中竞拍者的唯一均衡报价策略,并深入分析了反比佣金率的系数与竞拍者的均衡报价及拍卖参与者期望收益之间的关系。研究发现,竞拍者和卖者的期望收益与反比佣金率的系数k呈反向变动,拍卖行的期望收益与k呈同向变动。通过计算第一价格和第二价格拍卖模型中卖者和拍卖行的期望收益,发现获得的期望收益分别相等,说明著名的收益等价定理在基于反比佣金率约束的两种拍卖机制中仍然成立。进一步分析卖者和拍卖行的期望收益,分别构造出最优保留价和最优反比佣金率系数应该满足的条件,与现有研究文献的结论进行对比分析,说明该反比佣金率的设置及其结论的合理性。
自1961年Vickrey[1]对拍卖理论进行开创性研究以来,拍卖理论及应用受到广大学者的关注。在市场经济中,作为一种有效的价格均衡及资源配置机制,拍卖不仅在实践中被广泛使用,如艺术品、烟草、皮革、鱼类、花卉和无线电频谱使用权等拍卖活动[2],其理论也得到了深入研究[3-4]。最具有代表性的成果有Riley和Samuelson[5]及Myerson[6]建立的收益等价定理,为人们研究标准拍卖机制提供了基准。2020年诺贝尔经济学奖获得者Wilson和Milgrom曾分别研究了共同价值拍卖和关联价值拍卖,创造性地设计了非同质多物品的同步多轮拍卖机制,推动了拍卖理论向纵深发展[7]。在应用方面,关于石油、天然气、采矿权和木材采伐权的拍卖实践研究较多[8-9]。随着电子商务的兴起,网上拍卖风靡全球,主要有国外的eBay、Amazon、Yahoo、Sotheby和国内的易趣、阿里、京东等拍卖网站。因此,大量文献对网上拍卖机制进行了深入探究,丰富了拍卖理论研究的内涵,增强了拍卖理论研究的实用价值。
佣金作为一种常见的用于调整竞拍者、卖家和拍卖行之间收益分配的拍卖参数,一些学者对其进行了相关的理论研究。根据经济模型中变量的分类,可以将研究佣金的拍卖文献分为外生佣金率文献和内生佣金率文献两类。
假定佣金率是外生给定的文献主要有,Greenleaf等[10]将流拍罚金引入带有佣金的拍卖模型,发现拍卖行采取流拍罚金与较低佣金的组合比仅使用佣金具有帕累托占优,并且该策略鼓励卖者设置较低的保留价,首次将流拍罚金引入到拍卖机制中,但未涉及佣金率的设置问题。Ginsburgh等[11]研究了第二价格密封式拍卖中拍卖行分别对买家和卖家收取佣金时均衡报价和相关收益及福利的变化情况,发现较高的佣金率使买卖双方的境况都略有恶化,福利变化方向相同。虽然该文将佣金与福利关联起来,但仅分析了一种拍卖机制下的佣金收取情况。王彦等[12]首先研究了在独立私人价值模型和关联价值模型的框架下,第一价格和第二价格拍卖中获胜的竞拍者按成交价的一定比例向拍卖行支付佣金的情况,发现竞拍者的报价与佣金率成反向变动,但其期望收益与佣金率无关,两种机制中卖者的收益相等,收益等价定理仍然成立。毕志伟等[13]在前期研究[12]的基础上进一步研究了关联价值模型下第一价格和第二价格拍卖机制中佣金率对均衡报价和买卖双方收益的影响。虽然这两篇论文将佣金率引入到第一价格和第二价格拍卖机制中,但仅分析了佣金率对拍卖结果的影响,没有将保留价与之结合起来进行分析,也未探讨如何制定一个最佳的佣金率。Wang[14]进一步研究了第一价格和第二价格密封式拍卖中当佣金率是交易价格的线性函数时,风险中性的竞标者的均衡报价策略,并发现第二种拍卖机制的均衡报价策略是主导策略。但在研究第一价格密封式拍卖机制时,只分析了竞拍者的私人估价服从均匀分布这一特殊情况,因此结论具有一定的局限性。基于此,杨卫星等[15-]将Wang对第一价格拍卖中均衡策略的研究推广到一般分布的情形,并研究了卖者、拍卖行和竞拍者之间的期望收益问题,在一定程度上丰富了Wang的研究,但创新性略显不足。王明喜等[16]同时分析了第一价格和第二价格拍卖中佣金率和保留价与均衡报价和拍卖参与者期望收益之间的关系,并推导出最优保留价的表达式。这篇论文将研究扩展到第二价格密封式拍卖模型,但没有深入分析最优佣金率的设置。杨卫星等[17-19]进一步将佣金率具体化,分别研究了佣金率与成交价成反比和线性关系时第一价格和第二价格密封式拍卖模型的报价策略及收益问题,可是均未涉及最优保留价和最优反比佣金率的设置问题。
假定佣金率是内生决定的文献主要有,Rochet等[20]根据竞拍者人数是外生还是内生将拍卖市场分为单边市场和双边市场,分别探讨了两种市场机制中卖方接受的价格与税收(或佣金)之间的关系。Loertscher等[21]从理论上证明了当佣金率是内生变量时拍卖行在实际拍卖中使用卖者定价且收取变化很小的线性佣金的原因,并将Myerson的最优机制进行了一定的推广。刘树林等[22]对传统的第一价格拍卖模型进行了扩展,分析了带有佣金率和保留价时拍卖参与者之间的博弈行为,首次提出最优佣金率及其满足的条件,是国内研究佣金率和保留价的经典之作,为后续研究提供了新思路。冉茂盛等[23-24]运用博弈理论分别研究了网上一口价拍卖模型中最优一口价、最优佣金率和最优定额佣金的设置问题。其将佣金率应用于使用临时一口价的网上拍卖模型,丰富了佣金率的理论和应用场景。江朝力等[25]在广义第一价格拍卖机制下研究了互联网广告实时竞价中最优佣金率的设置问题,分析了保留价有无时需求方期望支出与佣金率的关系,进一步扩展了内生佣金率的适用范围,但仅分析了一种拍卖机制。虽然已有学者[17-18]研究了反比佣金率的存在性及其与拍卖参与者收益之间的关系问题,但对反比佣金率的设置还存在一定的不足,杨卫星[17-18]分别在对卖者和第二价格拍卖中竞拍者期望收益的推导中遗漏了一些特殊情况,并且均没有分析如何设置最优保留价和最优反比佣金率。另外,据2015年修订的《中华人民共和国拍卖法》第四章拍卖程序第四节佣金中的第五十六条和五十七条规定“收取佣金的比例按照同拍卖成交价成反比的原则确定”[26],因此研究拍卖机制中反比佣金率的设置具有一定的现实意义和实用价值。
综上,本文假设拍卖行向获胜的竞拍者收取的反比佣金率为c=k/b,采用贝叶斯-纳什均衡分析方法,通过分析第一价格和第二价格拍卖机制中竞拍者的期望收益,从而得到其均衡报价策略,并深入探讨了反比佣金率的系数对竞拍者的均衡报价策略以及拍卖参与者期望收益的影响,证明了对于竞拍者、卖者和拍卖行来说,两种机制是等价的,最后讨论了最优保留价和最优反比佣金率系数的设置问题。完善了现有文献所提出的拍卖模型中反比佣金率不能为零的缺陷,进一步丰富了收益等价定理并构造出最优保留价和最优反比佣金率系数应该满足的条件等内容,同时将所得结论与现有研究文献进行对比,证明了带有反比佣金率的拍卖模型的可行性,为拍卖行如何设置佣金率提供了有力的参考。
一、模型及符号
(一)模型假设
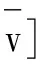
卖者和拍卖行决定选择第一价格或第二价格密封式拍卖模式进行拍卖,每个竞拍者根据自己对拍品的私人价值进行报价,其目标均是实现自身期望收益的最大化。将反比佣金率设置成c=k/b,其中k≥0,b为竞拍者的报价,且b>0。拍卖行采取单边佣金制,只有获胜的竞拍者按成交价的反比佣金率c向拍卖行支付佣金。卖者将保留价设置成r,且向竞拍者公开,因此拍品的最低成交价应为r,即竞拍者的估价应该满足v≥(1+k/b)r,那么竞拍者参与或不参与拍卖的无差异最低估价v*满足b(v*)=r,又因为v*=(1+k/b(v*))r,所以推出v*=r+k。因为估价低于v*的竞拍者不能获得正的收益,所以保留价r的设置将其排除在外,这里规定他们的报价为零,即当v 为了更加清晰地讨论,表1系统总结了文中两种拍卖模型使用的相关符号及其所代表的含义。此外,笔者使用下标F和S来区分第一价格和第二价格拍卖中的符号。在整篇文章中,递减、递增和单调性都是弱意义上的[27]。 表1 符号说明 在带有反比佣金率和保留价的第一价格密封式拍卖中,竞拍者基于期望收益最大化决定他们的报价,其均衡报价策略由定理1给出。 定理1当反比佣金率为c=k/b、保留价为r时,第一价格密封式拍卖中估价为v的竞拍者的对称均衡报价策略可以表示为 (1) 其中,v*=r+k,当v≥v*时,bF(v)是v的增函数,且有bF(v)≤v。 证明:根据第一价格密封式拍卖机制,当某个竞拍者的私人估价为v,而报价为B,其余竞拍者的报价策略为bF(v)时,该竞拍者赢得拍品后获得的期望收益可以表示为 (2) 在对称的贝叶斯-纳什均衡中,当B=bF(v)时,竞拍者获得最大的期望收益,从而竞拍者的最优报价策略满足以下一阶条件: 由于b(v*)=r,对上式简化后求解可得到式(1)。 上面证明了竞拍者选择均衡报价策略的必要条件,充分性的证明方法与王明喜等研究[16]类似,这里不再论证。因此,在第一价格密封式拍卖机制中,式(1)是竞拍者的贝叶斯-纳什均衡报价策略,也是其最优报价。再对式(1)求v的一阶偏导数可知,bF(v)是v的增函数。 推论1在带有反比佣金率c=k/b约束的第一价格拍卖机制中,竞拍者的对称均衡报价与保留价r呈同向变动,而与反比佣金率系数k呈反向变动。 证明:对式(1)分别求r和k的一阶偏导数,可知前者大于零,后者小于零,因此bF(v)关于r递增而关于k递减。 推论2在带有反比佣金率c=k/b约束的第一价格拍卖机制中,竞拍者的期望收益随保留价r和反比佣金率系数k的增大而减小,随r和k的减小而增大,即均呈反向变动。 证明:将式(1)代入式(2)可得竞拍者的期望收益为 其中,v≥v*且v*=r+k。因为在分布函数F给定的情况下,当r或k变大时,使得v*增大,从而使对应的积分区间变小,进而导致πF的值减小,因此竞拍者的期望收益与r和k均呈反向变动。 推论1和2的结论分别与刘树林等[22]论文中定理1的(ii)和(iii)及王明喜等[16]论文中推论1和2的结论一致,可见,在第一价格密封拍卖中,无论是佣金率还是某种形式的反比佣金率都会通过影响竞拍者的报价,从而影响竞拍者的期望收益。因此,竞拍者在参加带有反比佣金率和保留价的第一价格密封式拍卖时,其报价不仅低于他对拍品的私人价值,并且要比没有反比佣金率拍卖时的报价还低,这样才能尽可能减少受到的损失。 在没有佣金率和保留价的标准第二价格密封式拍卖中,竞拍者的报价等于其私人估价是弱占优策略[29]。王彦等[12]研究得出,在第二价格密封式拍卖中,当拍卖行设置了佣金率k时,竞拍者的最佳报价为v/(1+k),其中v为私人估价。王明喜等[16]给出了在佣金率c和保留价r同时存在的第二价格密封式拍卖中竞拍者弱占优均衡报价策略的表达式,该表达式与王彦等[12]论文中的式(11)相同,只不过此时估价v≥v*,其中v*=(1+c)r。本文通过设定反比佣金率的具体表达式,探讨其结果与现有文献的异同。 定理2当反比佣金率为c=k/b、保留价为r时,第二价格密封式拍卖中竞拍者的弱占优对称均衡报价策略为 bS(v)=v-k,v≥v*。 (3) 证明:由于对称性,设某个私人估价为v的竞拍者对应的报价为bS(t),其他竞拍者采用均衡报价策略,y表示其余n-1个竞拍者中的最高估价,则他的期望收益为 (4) 显然,当t=v时期望收益最大,根据包络定理和一阶条件有 解得 bS(v)=v-k 证毕。 经对比,当v*=v,k=0时,退化后的式(3)与McAfee等[28]论文中的结果一致。该结论与王明喜等[16]文中注记2的描述一致,说明本文研究结论的可靠性。 推论3在带有反比佣金率c=k/b约束的第二价格拍卖机制中,竞拍者的对称均衡报价与保留价r和参与竞拍的人数均无关,而与反比佣金率系数k呈反向变动。 证明:由式(3)可知,均衡报价仅由v和k决定,与r和n无关,且k的一阶偏导数小于零,因此,bS(v)关于k递减,而与保留价和竞拍者的人数均无关。 从定理2可知,与不带佣金率和保留价的传统拍卖模型相比,带有反比佣金率c=k/b的拍卖模型中竞拍者的均衡报价降低。这一结论与直觉相符,因为获胜的竞拍者需要向拍卖行支付佣金,所以竞拍者报价更加谨慎。 推论4在带有反比佣金率c=k/b约束的第二价格拍卖机制中,竞拍者的期望收益随保留价r和反比佣金率系数k的增大而减小,随r和k的减小而增大,即均呈反向变动。 证明:将式(3)代入式(4)并化简可得,竞拍者的期望收益为 由于v≥v*,v*=r+k且分布函数F已知,所以当r或k变大时,使得v*增大,从而使积分区间变小,导致πS的值减小,因此竞拍者的期望收益与r和k均呈反向变动。该结论与推论2一致,说明无论第一价格还是第二价格拍卖,当保留价为r、反比佣金率为c=k/b时,竞拍者的期望收益与r和k均呈反向变动。但与王明喜等[16]论文中推论4的结论不同,因为其只考虑了第二高报价大于等于最低估价v*这一种情况,因而所得结论具有一定的局限性。本文全面考虑了第二价格拍卖可能出现各种情况时竞拍者的期望收益。综上,竞拍者在参加带有反比佣金率和保留价的第二价格密封式拍卖时,报价要低于他对拍品的私人价值,否则会导致期望收益下降甚至为负。 根据前面推出的竞拍者均衡报价策略,在带有反比佣金率约束的第一价格和第二价格拍卖机制中,当保留价存在时分别计算卖者和拍卖行获得的期望收益,发现收益等价定理仍然成立。 证明:在第一价格密封式拍卖中,商品流拍后的收益和拍卖成功时的收益共同构成了卖者的期望收益,具体为 (5) 将式(1)代入式(6),对括号中的被积函数应用分部积分并化简得 (6) 在第二价格密封式拍卖中,商品流拍后的收益、仅有一个竞拍者的估价高于v*时的收益和至少有两个竞拍者的估价高于v*时的收益三部分共同构成了卖者的期望收益,具体表示为 (7) 此结论与杨卫星[17]论文中的结论不同,虽然其在计算第一价格和第二价格密封式拍卖中卖者的期望收益时,均忽略了商品流拍的情况,但不影响问题的本质;二者结论不同的关键原因是杨卫星研究中[17]在计算第二价格密封式拍卖中卖者的期望收益时,没有考虑仅有一个竞拍者的估价高于v*的情况,即忽略了式(7)等号右边的第二项。 推论5在带有反比佣金率c=k/b约束的第一价格和第二价格拍卖机制中,当卖者设置的保留价为r,拍品成功售出时卖者的期望收益与反比佣金率系数k呈反向变动。 综上,对于卖者而言,当他一旦确定了商品的保留价,就不必纠结于采用第一价格还是第二价格密封式拍卖,因为基于反比佣金率约束的两种拍卖机制给他带来的期望收益相等,关键是设置一个合理的保留价。 证明:因为只有当商品成功售出时拍卖行才能获得收益,所以在第一价格密封式拍卖中,由式(5)可知,拍卖行的期望收益为等号右侧第二项乘以反比佣金率k/b,即为 (8) 同理,在第二价格密封式拍卖中,拍卖行的期望收益为式(7)等号右侧后两项分别乘以对应的反比佣金率k/r和k/b,即为 (9) 如果仅分析存在保留价的情况,而令反比佣金率为0时,退化后的定理3和定理4就与Riley等[5]论文中命题1的结论一致。 推论6在带有反比佣金率c=k/b约束的第一价格和第二价格拍卖机制中,当卖家设置的保留价为r时,拍卖行的期望收益与反比佣金率系数k呈同向变动。 证明:对式(8)或式(9)求k的一阶偏导数,其结果大于零,所以推论6成立。该结论与直觉相符,因为c=k/b,所以c随k的增加而变大,拍卖行的收益因此而增加,反之亦然。 进一步研究发现: 因此,带有反比佣金率的第一价格密封式拍卖中卖者和拍卖行的收益之和等于不带佣金时卖者的期望收益。同理,带有反比佣金率的第二价格密封式拍卖中卖者和拍卖行的收益之和等于不带佣金时卖者的期望收益。由此可以得出推论7。 推论7在第一价格和第二价格密封式拍卖中,与不带佣金时的收益相比,反比佣金率的设置减少了卖者的期望收益,该部分全部转化为拍卖行的期望收益。 综上所述,定理3和定理4说明,在带有反比佣金率约束且设置了保留价的第一价格和第二价格拍卖规则中,卖者和拍卖行无论选择哪种拍卖机制,获得的期望收益均相等,即著名的收益等价定理仍然成立。因此,对于卖者和拍卖行来说,不必为选择哪种拍卖方式而困扰,关键是设置恰当的保留价和反比佣金率系数,将商品以合适的价格拍出,尽量避免流拍,从而实现二者的期望收益最大化。 卖者如果设置一个较高的保留价可能会使竞拍者产生反感,甚至直接将部分有意向的竞拍者拒之门外;如果设置一个较低的保留价,则对竞拍者的约束性较差,失去了保留价原有的作用,还会给卖者带来一定的损失。因此对于卖者而言,制定一个恰当的保留价显得尤为重要。 定理5基于反比佣金率c=k/b约束的第一价格和第二价格密封式拍卖中,卖者设置的最优保留价r应满足 (10) 证明:根据卖者的期望收益表达式(6),对其求r的一阶偏导数,从而得到最优保留价应满足以下一阶条件: (11) 结合v*=r+k,可以解出式(10)。 上面是最优保留价r存在的必要条件,下面证明r存在的充分条件。对式(11)进一步求r的偏导数,得到 因为当r满足式(10)时该式小于零,所以卖者的期望收益取得极大值,从而说明此时的r是卖者的最优保留价。 推论8最优保留价r随反比佣金率系数k的增大而减小,随k的减小而增大,即呈反向变动。 证明: 对式(10)用隐函数求导方法可得 因此,r与k的变动方向相反。 推论9最优保留价r随商品流拍价值v0的增大而增大,随v0的减小而减小,即呈同向变动。 证明:与推论8的证明类似,对式(10)用隐函数求导方法可得 因此,r与v0的变动方向相同。推论9的结论与实际相符,对于卖者来说,当拍品的私人价值较高时,他自然会制定一个较高的保留价,反之则制定较低的保留价。 通常佣金问题由拍卖行决定,如果拍卖行设置的反比佣金率过高,可能会影响竞拍者和卖者的积极性,甚至导致竞拍者恶意降低报价;如果设置的反比佣金率过低,则对竞拍者的约束性较差,降低拍卖行的期望收益。因此,制定一个恰当的反比佣金率显得尤为重要。 假设卖者的保留价r是外生给定的,根据拍卖行的期望收益可以推出最优反比佣金率系数k应满足的条件,如定理6所示。 定理6基于反比佣金率c=k/b约束的第一价格和第二价格密封式拍卖中,拍卖行设置的最优反比佣金率系数k应同时满足 (12) (13) 证明:根据式(8)或式(9),对其求k的一阶偏导数,从而得到最优反比佣金率系数k应满足以下一阶条件: 于是,可以解出式(12)。 上面是k存在的必要条件,下面证明k存在的充分条件。对上式进一步求k的偏导数,化简后得 显然,当式(13)成立时上式小于零。 因此,当k同时满足定理6中的两个条件时,拍卖行的期望收益取得极大值,从而说明此时的k是拍卖行的最优反比佣金率系数。 为了说明本文设置的反比佣金率的可实施性和所得结论的正确性,下面通过一个数值算例来验证。假设拍卖市场上只有一个卖者、一个拍卖行和两个竞拍者竞拍一件不可分割的拍品,即n=2,商品流拍后的残值v0=0.15,竞拍者对拍品的私人估价v~U[0,1],根据概率论知识可得F(v)=v,对应的概率密度函数为f(v)=1。为了简化所研究的问题,不考虑拍品的生产成本。当给定r=0.3时,根据式(12)可以求出k=0.386,该值满足式(13),可见0.386是最优的反比佣金率系数,因此定理6是可行的。此时带有反比佣金率约束的第一价格和第二价格拍卖机制中均衡报价和期望收益的结果如图1所示。 图1 两种机制下均衡报价和期望收益的比较 由图1可知,当根据给定的保留价确定出最优反比佣金率系数后,除竞拍者的最高估价等于最低估价v*这种特殊情况外,第一价格密封式拍卖模式中获胜的竞拍者的均衡报价明显低于第二价格密封式拍卖时的均衡报价,即bF(v) 结合我国拍卖法律对佣金率的规定,改进现有文献中反比佣金率设置的不足,完善其部分推导缺陷,并给出了最优保留价和最优反比佣金率系数应满足的条件,使带有反比佣金率的拍卖模型更加符合实际。通过对竞拍者、卖者和拍卖行之间的博弈行为进行分析,得到如下结论:(1)竞拍者在两种拍卖模式中均存在贝叶斯-纳什均衡报价策略,且均衡报价都低于获胜者的真实估价,说明由于反比佣金率和保留价的存在,竞拍者的报价更加谨慎。尤其是参加第一种拍卖时,竞拍者的报价要更低,否则会导致收益下降甚至为负。(2)竞拍者的期望收益与保留价r和反比佣金率的系数k均呈反向变动,表明r和k对竞拍者有消极作用,因此卖者和拍卖行应该设置合理的保留价和反比佣金率系数,从而激励竞拍者参与拍卖。(3)经比较分析发现,在具有反比佣金率约束的第一价格和第二价格拍卖模式中卖者和拍卖行获得的期望收益分别相等,说明在同时考虑反比佣金率和保留价时著名的收益等价定理仍然成立。因此,对于卖者和拍卖行来说,不必纠结于采用何种拍卖形式,因为两种拍卖形式给他们带来的期望收益是相等的。(4)通过分别对卖者和拍卖行的期望收益求r和k的偏导数,得到最优保留价和最优反比佣金率系数应该满足的条件;进一步研究还发现最优保留价与反比佣金率的系数呈反向变动,而与商品的流拍价值呈同向变动。因此,卖者一方面应合理估计拍品的私人价值,另一方面应与拍卖行共同协商确定出最优的保留价和反比佣金率,避免商品流拍,从而实现双赢。 本文通过具体算例验证了上述结论的正确性,但研究还存在一定的局限性,以下问题需要深入探讨:进一步丰富反比佣金率的表示形式、优化结论使其在其他拍卖机制中具有可移植性和健壮性以及拓展最优保留价和最优佣金率的研究空间。(二)符号说明

二、均衡报价策略
(一)第一价格密封式拍卖
(二)第二价格密封式拍卖
三、期望收益
(一)卖者的期望收益
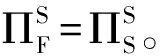

(二)拍卖行的期望收益
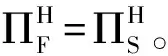


四、最优保留价和最优反比佣金率系数的确定
(一)最优保留价
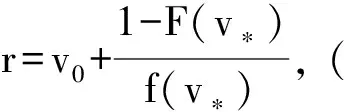
(二)最优反比佣金率系数
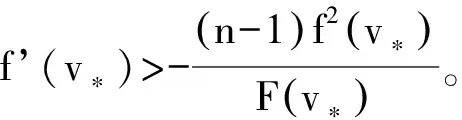
五、算例验证

六、结论与展望
