考虑道路损毁情况的应急物流LRP研究

袁 涛，蔡 佳，郑 磊，户佐安

（1. 中铁二院工程集团有限责任公司 土木建筑设计研究二院，四川 成都 610031；2.西南交通大学交通运输与物流学院，四川 成都 611756)

0 引言

自然灾害造成的重大事故给人们的生命和财产带来了巨大的损失，灾后应急救援物资的快速送达能有效减少人员伤亡，及时为灾后重建提供物资保障。在应急物流定位配送问题(Location Routing Problem，LRP)的研究中，应当考虑在地震、雪灾等自然灾害发生后，道路网受到不同程度的损坏，可能发生车辆运输受阻甚至中断的实际情况。此时选择可靠性高的配送路径，不仅能有效避免应急物资在公路运输过程中发生滞留，也能降低车辆的运输风险。因此，在地震、雪灾、洪水等灾难发生后，结合道路实际状况制定应急物流网络选址及配送方案，以满足应急救援需求和减少应急救援成本，是应急物流网络优化的重要组成部分。

针对考虑道路状况的应急物流配送车辆路径问题(Vehicle Routing Problem，VRP)已有一定研究成果。程光[1]分析了道路状况对运输速度和道路连通可靠度的影响。孙君[2]认为道路受损和断裂不仅会降低其容量和流量，还将导致两端节点功能受损。王晶等[3]考虑了道路连通可靠度约束，以救援总时间最短为目标构建了应急物资配送模型。曹庆奎等[4]考虑了道路修复时间，建立以时间和成本最小为目标的模型求解两层配送网络的物资调度问题。陈森等[5]考虑道路修复的物资消耗，研究路网结构未定条件下路网结构和车辆路径的联合优化。韩会鹏[6]考虑了道路修复状态的更新对物资配送带来的影响并构建物资调度决策模型。李巧茹等[7]以最大化车辆行驶路径可靠度、最小化系统物资未满足度为目标建立模型，以保证运输的安全性和物资分配量的效用性。在应急物资配送中考虑道路状况能有效提高运输方案的可靠性，但其配送方案是基于已知的运输网络而制定的，而在实际救援中，除受灾点以外的应急物流设施在一开始往往是未定的。

应急物流设施定位决定了应急物流网络系统的结构形态，应急物资运输路径研究则进一步对具体配送路径进行安排和优化，因而根据运输需求对两者进行组合优化更适用于实际救援情景。近年来，越来越多的学者对应急物流设施选址和路径优化的联合问题进行研究。Rezaei等[8]考虑易腐物资的存储和配送特点，建立鲁棒模型解决应急设施预定位和物资分配问题。刘长石等[9]考虑震后配送中心失效的情况，以最坏失效情景下的需求点覆盖期望最大、应急物资总配送时间最短为目标建立模型。帅斌等[10]对基于时变网络下应急物流中的有害物品运输建立了多目标LRP模型，并采用改进的蚁群算法求解。李伟利[11]研究考虑受灾点优先级和满意度的单级静态和多级动态应急物流网络优化问题。LRP模型充分体现了运输网络设施定位与路径优化相互影响和相互依赖的关系，但现有研究并未将其与道路状况结合。

总的来看，应急物流VRP和LRP已经有了较多的成果，但将应急物流LRP和道路修复、道路可靠性及多式联运综合考虑的研究较少，且已有研究多考虑道路受损对可靠度的影响，而忽略对通行时间的影响，此时得出的配送或选址方案可能造成应急物资的延迟送达，违背了应急物流及时快速的运输要求。因此，研究针对应急物资供应点、配送中心、受灾需求点构成的多级LRP问题，考虑道路损毁和道路修复对应急救援的影响，建立公路、铁路、直升机联合救援成本最小的应急物流选址、路径优化、道路修复集成优化模型，并利用软件求解。

1 考虑道路损毁的灾后应急物流网络

当灾难发生后，若受灾点近距离范围内有大型救援物资供应点，可以由供应商直接将物资运送至受灾点。但在实际情况中，距离灾区较近的供应点通常自身受灾情影响无法正常运作，且单个供应点同时为多个受灾点提供援助，需要其在满足快速生产、集货的同时还具备完善的物流设备和功能。当供应点距离受灾点较远，或供应点无法同时满足生产和运输要求时，可结合受灾区域交通、地理情况，建设若干个具有储存、装卸搬运、流通加工等基本物流功能的配送中心，用来接收上游供应的应急物资，通过理货、配货后，向下游灾区需求点配送救援物资。由于应急物资配送中心建设周期短、规模小、建设成本低的特点，可在短时间内改建或新建多个配送中心，同时向多个受灾点提供救援。此时的应急物流网络为3级2层网络结构，第一级为供应点，包含各类应急物资和装备的大型制造商及供应商，可通过公路、铁路、直升机等运输方式向应急物资配送中心输送大批量救援物资，再由应急物资配送中心承担中转和配送任务，通过公路和直升机运输方式将救援物资配送至应急物资需求点。三级结构的应急物流网络各级节点分工明确，适应性强，因而仅需重点研究有配送中心的应急物流LRP问题。应急物流多式联运网络示意图如图1所示。

应急物资从供应点运送至配送中心，为应急物流网络的供应层，可选择公路、铁路及直升机3种运输方式，由于供应点距离受灾区域较远，可认为供应层道路不受灾害影响。物资由配送中心运输至需求点，为应急物流网络的配送层，相比供应点，配送中心更加靠近受灾区域，当灾害发生后，配送层公路或铁路可能出现落石堵塞、开裂、变形甚至断裂的情况，公路运输可对道路进行简单清扫或修复后较快恢复通行，而铁路运输对轨道要求高，为避免造成脱轨或设备损坏，需要对轨道进行完善的修理和检查。此外，配送层服务对象为应急物资需求点，运输规模较小，运输距离较短，无法充分体现铁路运输的规模效益，且列车在车站停留时间较长，不利于物资的及时送达。基于以上因素，不考虑配送层的铁路运输。当配送层道路损毁严重导致车辆无法通行时，可选择直升机进行协同运输，即配送层运输方式为公路运输和直升机运输。配送层车辆或直升机完成本线路救援任务后留在最后配送的需求点，需求点接收足量的救援物资后即视为救援结束。

对于应急物资配送层，利用无人机航拍等技术可事先获取应急物资需求点的位置和道路损毁情况，即道路的连通可靠度已知，未受损害的道路可靠性为1。由于道路受到损害的等级越高，道路的连通可靠性越小，运输速度越小[1]，因而道路状况对运输速度的影响可通过可靠度表达，即认为道路的可靠度与运输时间呈正相关关系。为保障车辆的正常运输和提高路段的连通可靠度，可选择对部分道路进行修复，修复后的道路连通可靠度可恢复为1，但会产生由道路受损单元数决定的修复时间和修复成本。在整个应急救援过程中，不考虑运输方式间的中转费用及中转时间。

由以上描述可知，只有合理选择应急物资配送中心，决策道路修复次序，分配车辆和直升机运输量，规划可靠的运输路径，才能使各受灾点应急物资需求在规定时限内得到满足的同时控制救援成本。

2 考虑道路损毁情况的应急物流LRP模型

2.1 模型假设

以运输费用、配送中心固定建设费用、道路修复费用之和最小为目标函数，考虑救援时间限制、配送中心容量限制、网络最低通行可靠度限制等约束条件建立模型，模型假设如下。

（1）任意节点间直升机运输距离为节点间的直线距离，公路运输距离、铁路运输距离为直线距离按一定比例折算。

（2）若两点间无道路直接连接，该两点间的公路运输距离为无穷大。

（3）供应点不可直接向需求点运输救援物资。

2.2 模型构建

救援总成本包括配送中心固定建设费用、供应层与配送层的运输费用及道路修复成本，计算公式为

式中：Z为救援总成本，元；K为应急物资配送中心备选集合；Hk为0-1变量，若在k点建设配送中心，则Hk= 1，否则Hk= 0；C为单个配送中心的建设费用，元；I为应急物资供应点集合；M为运输方式集合，M= {M1，M2} = {{m1h，m1r，m1p}，{m2h，m2p}}，M1为供应层运输方式集合，M2为配送层运输方式集合，m1h，m1r，m1p分别为供应层公路、铁路、直升机运输；m2h，m2p分别为配送层公路、直升机运输；Xikm为0-1变量，若供应点i到配送中心k用方式m运输，则Xikm= 1，否则Xikm= 0；Fikm为供应点i到配送中心k方式m运输的货流量，kg；Dikm为供应层点i到点k运输方式m的运输距离，km；Cm为运输方式m的单位运输费用，元；J为应急物资需求点集合；Ykjm为0-1变量，若配送层点k到点j用方式m运输，Ykjm= 1，否则Ykjm= 0；dkjm为配送层点k到点j运输方式m的运输距离，km；fkjm为配送层点k到需求点j方式m运输的货流量，kg；λ为单元受损道路修复费用，元；Ckj为点k到点j间道路受损单元数；Skj为0-1变量，若修复点k到点j之间道路，Skj= 1，否则Skj= 0。

其中，道路受损单元数Ckj的计算公式为

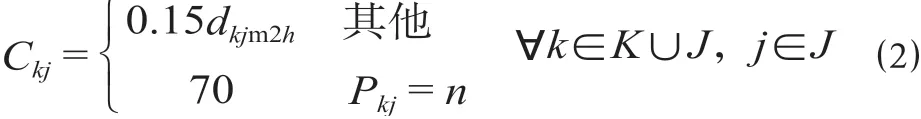
式中：dkjm2h为配送层道路受损后点k到点j公路运输距离，km；Pkj为点k、点j之间路段通行可靠度，n为极小的负数，若点k与点j间道路完全阻断，则Pkj=n。

线路通行可靠度计算方法参考文献[12]，即认为一条完整线路的通行可靠度为路径中各个路段可靠度的最小值。

式中：Pl为路径l通行可靠度；Plij为路径l上点i、点j之间路段的通行可靠度。

采用公路运输时，参考文献[3]中道路通行可靠度与实际通行时间的关系描述，配送层任意点k与点j之间的运输时间计算公式为

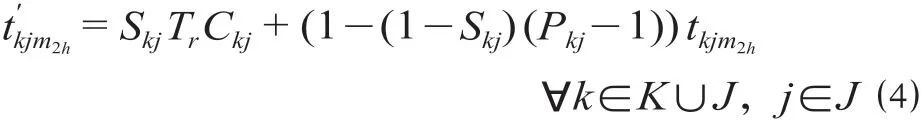
救援过程中需满足配送网络最低通行可靠度约束、供应点存放量约束及配送中心容量约束。

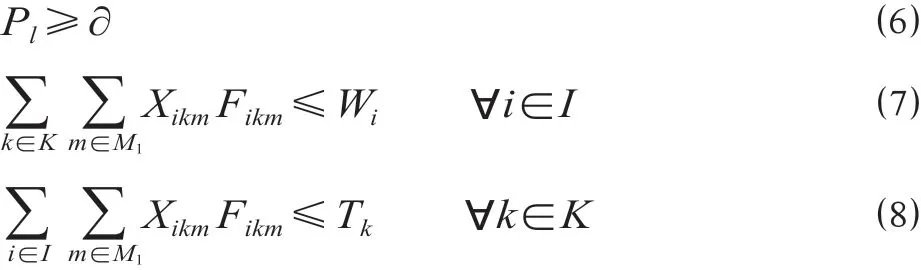
式中：∂为配送网络可接受的最低通行可靠度，∂∈[0，1]；Wi为供应点i物资存放量，kg；Tk为备选配送中心k的容量，kg。

救援结束时，从配送中心至受灾点的运输时间不得超过配送层能接受的最大运输时间，且任意受灾点接受的物资总量应满足其需求量。

式中：TOj为救援物资到达点j的时间，h；TL为配送层能接受的最大运输时间，h；Qj为需求点j对物资的需求量，kg。

在整个运输网络中，某配送中心建设后，供应点即向其提供救援物资，再由该配送中心将物资完全配送至受灾点。各配送中心之间不可进行货物运输，且一个受灾点仅接受一次救援，约束如下。

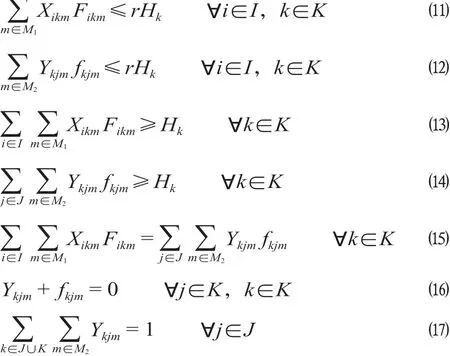
式中：r为极大的正数。

LPR模型还需满足的其他约束条件如下。

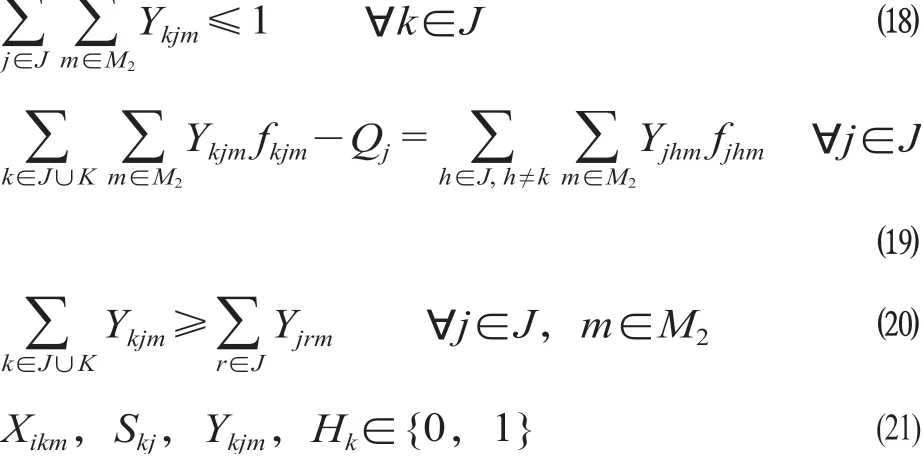
公式 ⒅ 表示接受救援的点可以为该路线的配送中间点或终点，若点k为配送路线终点时，则车辆或直升机留在点k，此时；公式 ⒆表示对任意受灾点而言，运输至该点的货流量减去该点自身需求等于从该点运出的货运量，即节点货流平衡约束；公式 ⒇ 表示路径的连续性；公式(21)为变量的0-1约束。

3 算例及结果

3.1 算例设计

当城市6突发地震后，与之直接相连的4条道路受损严重，城市6与城市2，5，7，10之间的公路通行完全中断，网络中其他道路均有不同程度损坏。现有A，B共计2个物资供应点和7个应急物资需求点，供应点距离需求点较远。对受灾区域附近未受灾的城市进行定性分析，根据交通便利、地形平坦、具备建设条件的原则可确定4个应急物资配送中心备选点，应急物资运输网络如图2所示。

图2 应急物资运输网络图Fig.2 Transportation network of emergency supplies

图2 中，A，B供应点向配送中心运输物资为供应层，运输方式包括铁路、公路及直升机运输，应急物资配送中心向需求点配送物资为配送层，运输方式包括公路和直升机运输。由于直升机可在任意两点间进行运输，故在图2中仅表示公路运输和铁路运输所需通道，即各点之间的连接道路和铁路。图2中两点间相连路径对应的数字分别为铁路运输距离、公路运输距离及公路运输的道路通行可靠度，由于供应层道路未损坏，其道路通行可靠度均为1。供应点物资供应量、配送中心容量及受灾点需求量如表1所示。

表1 供应点物资供应量、配送中心容量及受灾点需求量 kgTab.1 Supply amounts of supply points, distribution center capacities, and demands of disaster-stricken points

供应点至备选配送中心的直线距离如表2所示。配送层直线距离如表3所示。取节点间公路运输距离与直线距离的比值为1.15，铁路运输距离与直线距离的比值为1.3[13]。

表2 供应点至备选配送中心的直线距离 kmTab.2 Straight-line distances from supply points to available distribution centers

各种运输方式的单位运输成本及运输速度如表4所示。

表4 单位运输成本及运输速度Tab.4 Transportation costs per unit and transportation speeds

固定建设费用设为12 000元，单元道路修复费用λ为1 200元，单元道路修复时间Tr为1 h，可接受的最低通行可靠度∂为0.7。

3.2 结果分析

利用软件求解上述模型，当配送层时间限制为12 h时，选择的配送中心数量为3个，即配送中心1，3，4，救援运输费用为8 138 715元。供应层运输方式均为铁路运输，供应点至配送中心货物分配如表5所示。

表 3 配送层直线距离 kmTab.3 Straight-line distances of distribution layer

表5 供应点至配送中心货物分配 kgTab.5 Distribution of goods from supply points to distribution centers

配送层运输方式为直升机和公路运输结合，道路修复方案为不修复任意一条道路，救援路径与运输方式如图3所示。救援物资最晚到达受灾点9，救援持续的时间为8.79 h，3条配送路径的通行可靠度最低为0.8。

图3 救援路径与运输方式Fig.3 Rescue paths and transportation modes

当时间限制逐渐变大，得到的应急救援及道路修复方案如表6所示。

由表6可以看出，当配送层救援时间限制大于36 h时，选择修复道路2—7能够减少救援成本，但同时使得救援时间增加至30.88 h，此时由于道路2—7经过修复通行可靠度提升为1，节点2与节点7之间采用公路运输时能够满足网络最低可靠度约束，故配送中心选址方 案 由1，3，4变 化 为1，2，4。当救援时间限制大于96 h时，选址方案未发生变化，但由于修复了道路2—7与5—6，救援物资均采用了单位费率更低的公路运输，救援成本大幅减少，但道路5—6的修复时间达到了70 h，导致城市8成为最后一个接受救援物资的城市，总的救援时间增加至76.22 h。继续增大救援时间限制后，道路修复和运输方案均不再变化。

表6 应急救援及道路修复方案Tab.6 Emergency rescue and road repair schemes

应急救援通常随着灾情发展分多个阶段进行，若配送初期建立应急物资配送中心1，2，4，为避免资源浪费，应急救援的其他阶段将继续使用已建的配送点。道路修复与救援成本关系如图4所示。

受灾初期，对救援物资的需求紧迫，此时不宜选择修复道路，随着灾情的稳定，配送时间限制逐渐增加，修复道路带来的成本收益开始显现。当时间限制扩大至36 h时，仅修复道路2—7能够在满足救援需求的同时减少运输费用；当救援时间限制进一步扩大到84 h时，仅修复道路5—6或同时修复道路5—6与2—7均能减少救援后期的运输费用，修复道路5—6与2—7相比仅修复道路5—6，会增加道路修复费用34 200元，但使得运输路径2—7—8由直升机运输变为公路运输，减少了运输费用458 350元，从而使得总救援费用大幅减少。同时，由图4可得出，当受到道路修复物资和修复人员等限制而只能选择修复1条道路时，道路5—6的抢修效益明显大于道路2—7，故在道路修复时应首选对救援带来成本节约更大的道路。

图4 道路修复与救援成本关系Fig.4 Relationship between road repair and rescue cost

4 结论

研究构建了由应急物资供应点、配送中心、需求点组成的多级救援网络，考虑灾后道路损毁对通行时间和可靠度的影响，建立了集配送点选址、货流调配、运输方式选择、配送路径优化和道路修复为一体的应急物流网络优化模型，并求解模型得出有效的选址、配送及道路修复方案，对结果进行分析得到以下结论。

（1）在救援的初期选择修复道路不仅会产生修复成本，且不符合应急救援高时效性的要求。

（2）在救援的中后期，救援物资运输的时间约束放宽，此时修复道路虽然会产生一定修复成本，但也能通过改善道路通行状况、减少车辆通行时间，从而改变配送路径的选择，减小运输费用，降低总的救援成本。

（3）在道路修复时，应在保证运输需求的前提下，选择能为救援后期带来最大成本节约的道路有利于救援成本的控制。