一种求解交通网络中最短路径问题的人工蜂群算法

王 玉, 申铉京, 周昱洲， 林鸿斌

(1. 吉林大学 计算机科学与技术学院, 长春 130012； 2. 吉林大学 软件学院， 长春 130012)

随着智能交通系统的应用越来越广泛, 车辆路径规划作为智能交通系统的一项基本功能, 因而得到越来越多的关注. 目前, 对于静态交通网络的车辆路径规划研究已有很多结果： 张波良等[1]对静态路网中的各算法进行了比较; TNR算法[2]用表查找完全替代了Dijkstra搜索, 使其加速比达100多万; 文献[3]进一步将TNR算法与边标记法相结合, 加速比提升至300多万. 但实际交通网络总在不断变化, 而忽视路网环境的变化很可能使车辆陷入交通拥挤的状态中, 因此, 在静态交通网络中获取的最短路径通常不能很好地满足人们出行的需求, 动态网络下的路径规划更具有实际意义. 交通路网中各条道路的通行时间是不断变化的, 即满足网络中弧的行走时间是时间的函数这一特性. 故交通网络是一个时间依赖网络(简称TDN网络). 谭国真等[4]将TDN网络分为先进先出(FIFO)型与非FIFO型, 并证明在FIFO型网络中可采用Dijkstra算法求解, 而非FIFO网络则不可行; 王海梅[5]通过对路网进行分析认为, 当路径寻优的对象为机动车辆时, 道路交通网络具有FIFO网络的特性.

本文针对在TDN网络中求解最短路径问题, 提出一种基于人工蜂群算法的解决方案, 相比于遗传算法[6], 该算法具有控制参数少、 易实现的特点. 同时, 根据FIFO网络的特性对算法中的路径选择策略进行改进, 进一步提升算法的执行效率.

1 问题描述

定义1[7]图G={V,E,F(t)}称为时间依赖网络TDN, 其中V={1,2,…,n}为顶点集合,E={(i,j)|i≠j,i,j∈V}为边集合,F(t)={fi,j|(i,j)∈E}为边权函数的集合,fi,j(t)为时间t的函数,t∈[a,b],b>a≥0.

定义1中的TDN网络是连续的, 而在研究交通网络时, 由于交通网络在连续的一段时间内变化较小, 因此为简化计算, 通常将交通网络离散化处理. 离散时间情形下的TDN网络模型为

G={V×T,E,F},

其中:T为感兴趣的时间闭区间[t0,tm],T={t0,t0+Δ,t0+2Δ,…,t0+(M-1)Δ,…,tm},Δ表示一段较短的连续时间, 本文设Δ=5 min;V×T={(i,tj)|i∈V,tj∈T}表示节点的状态空间, 有序对(i,tj)表示节点的一个状态, 节点i在不同时间段内可能有不同的状态.

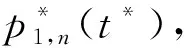
2 人工蜂群算法

人工蜂群(artificial bee colony, ABC)算法[8]是一种基于群智能的全局优化算法, 其通过模仿蜂群寻找食物的过程解决问题. 该算法包括3类核心元素： 食物源、 雇佣蜂和非雇佣蜂; 以及两种基本操作： 招募蜜蜂和放弃食物源. 其中: 食物源表示待解决问题的可能解； 雇佣蜂在食物源附近进行领域搜索, 并通过“8”字舞的方式分享食物源信息; 非雇佣蜂可分为观察蜂和搜索蜂, 观察蜂在获取雇佣蜂的信息后根据食物源的质量选择是否前往, 搜索蜂寻找新的有价值的食物源.

人工蜂群算法是为解决函数优化问题而提出的, 目前在多领域广泛应用, 本文对该算法的编码方式以及种群生成方式进行离散化处理, 以适应最短路径问题.

2.1 编码策略

因为车辆路径规划属于离散问题, 所以本文采用自然数编码的方式, 即采用自然数对路网中的每条边进行编号, 而一条路径是由这些编号组成的队列, 队列中的编号允许重复. 由于实际应用中因为交通规则的限制, 因此最优路径中可能会出现环路.

2.2 路径选择策略

人工蜂群算法的收敛依赖于一个具有多样性的种群, 本文用每条从起始节点至目的节点的可行路径表示种群中的每个个体. 其中路径的搜索过程为： 从起始节点开始, 按照路径选择策略选取一个邻接节点作为下一个节点, 持续此操作, 直至目的节点. 因此, 路径选择策略直接影响路径选择的优劣, 进而影响种群的收敛速度与效果.

文献[9]在蚁群选择路径时加入了方向引导, 该方法可有效缩小搜索空间. 在真实路网中由于地形和交通规则等限制, 并非所有的边都可以到达终点, 所以在有些边上可能会出现无下一条路可选的情形. 为防止下次路径搜索时再进入该边, 本文加入一个禁忌表用于记录该类边. 路径搜索策略(为叙述方便， 记为路径选择策略1)如下：

为方便描述, 设当前路径的终点为j.

步骤1) 搜索所有与当前路径终点相连接的边, 加入边队列;

步骤2) 从候选队列选取一条边ei, 并将其出队;

步骤3) 判断边ei是否可以驶离当前路径终点, 如果可以则转步骤4); 否则转步骤7);

步骤4) 检查边ei是否存在于禁忌表T中, 如果不存在则转步骤5)； 否则转步骤7)；

步骤5) 检查边ei是否违反转弯限制, 如果不违反则转步骤6)； 否则转步骤7)；

步骤6) 做边ei起点到终点的向量vi, 计算vi与vj的夹角, 将边ei加入候选列表, 转步骤7);

步骤7) 判断边队列是否为空, 如果为空则转步骤8)； 否则转步骤2);

步骤8) 判断候选列表是否为空, 如果为空则将边ei加入禁忌表； 否则转步骤9)；

步骤9) 计算候选列表中每条边的选择概率；

步骤10) 采用轮盘赌策略在候选列表中选择一条边加入路径, 并计算加入后的路径成本.

2.3 领域搜索策略

一条路径的领域搜索策略为： 在路径的第2个节点至第(n-1)个节点中随机选择一个节点, 并删除此后全部节点; 从该节点开始, 按照路径选择策略重新搜索一条能到达目的节点的路径.

2.4 人工蜂群算法执行步骤

1) 初始化参数, 产生初始食物源;

2) 进行迭代判断, 若不满足结束条件则转步骤3)； 否则转步骤7)；

3) 雇佣蜂到蜜源附近进行领域搜索发现新的食物源, 若新食物源优于原食物源, 则用新食物源替代原食物源, 否则保持原食物源;

4) 跟随蜂根据雇佣蜂分享的信息按食物源的质量进行概率选择食物源, 并在食物源附近进行领域搜索;

5) 判断雇佣蜂领域搜索次数, 当达到控制参数阈值时, 如仍未找到更优的食物源, 则放弃其对应的食物源, 将雇佣蜂转化为侦查蜂寻找下一个新的食物源；

6) 记录当前最优解；

7) 输出最优解.

3 改进人工蜂群算法

3.1 算法可行性

人工蜂群算法可适用于FIFO网络和非FIFO网络, 图1为采用路径选择策略1生成的一条路径. 由图1可见, 当取路段长度作为路网中边的权值时(即在静态路网中), 在该静态路网中存在若干条更短的路径(图1中红色路段), 在替换原路径中部分子路径后一定可以使原路径的距离更短.

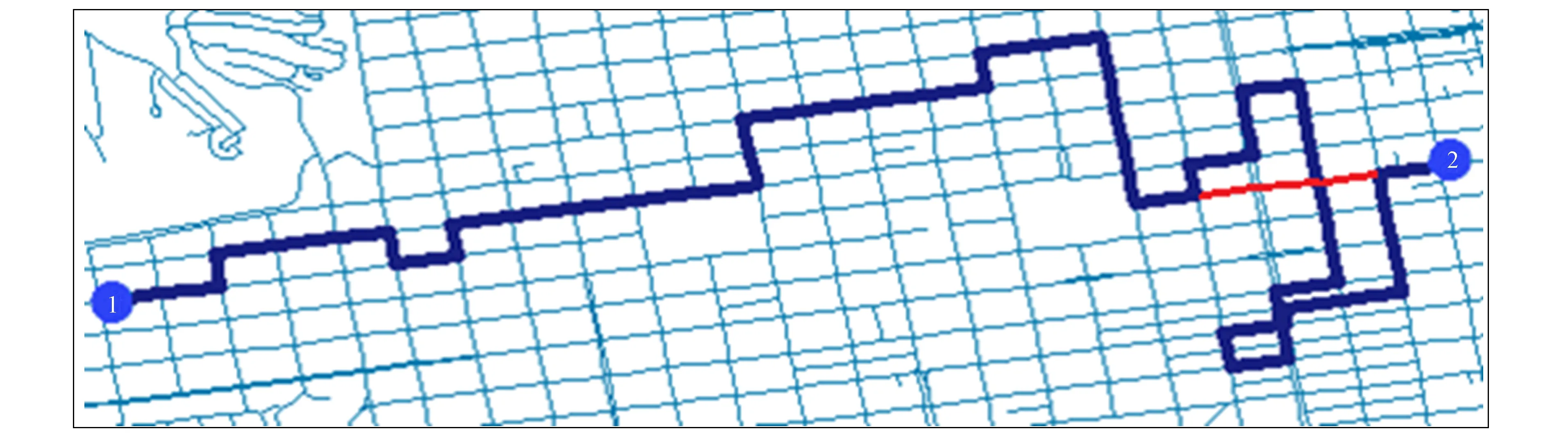
图1 采用路径选择策略1生成的一条路径Fig.1 Path generated by path selection strategy 1

定理1[10]如果网络中每个圈的长度为非负, 则网络中每条路径的长度不小于相应的最短路径长度, 且每条最短路径的子路径也是最短路径.

定理2[10]在时变FIFO网络中, 如果tS时刻从节点nS出发到达节点nD的最短时间路径为

SP(nS,nD,tS)={(nS,tS),(n1,t1),…,(ni,ti),(ni+1,ti+1),…,(nj,tj),(nD,tD)},

则最短路径SP(nS,nD,tS)的子路径{(nS,tS),(n1,t1),…,(ni,ti)}和{(ni,ti),(ni+1,ti+1),…,(nj,tj),(nD,tD)}也一定是最短时间路径, 其中ni是最短时间路径上的任一中间节点.

对于TDN网络, 若使用更短路径替代原路径中部分子路径的方法也成立, 则蜂群算法中食物源的整体质量将会提升, 进而可通过减少食物源的数量以及算法迭代次数提升人工蜂群算法的运行速度. 由定理1和定理2可知, 该方法对于FIFO网络成立, 即在FIFO网络中, 当原路径中某一段被另一段通行时间更短的子路径替代时, 原路径的通行时间也会缩短.

3.2 改进路径选择策略

在路网中能替代原路径的时间更短子路径可以有多种, 但实际上在搜索一条到达目的节点的路径过程中, 每向路径中加入一条路段之前都会遍历到与该路段相邻的路段, 而这些相邻路段中可能存在更短子路径[11-13]. 图2～图4分别为在路径搜索时可能遇到的3种情形. 由图2可见, 当边ab加入路径时记录节点b, 当路径加入边bf时检查节点b是否有过记录, 若存在路径abf能通行, 则用其代替原子路径abcdebf.

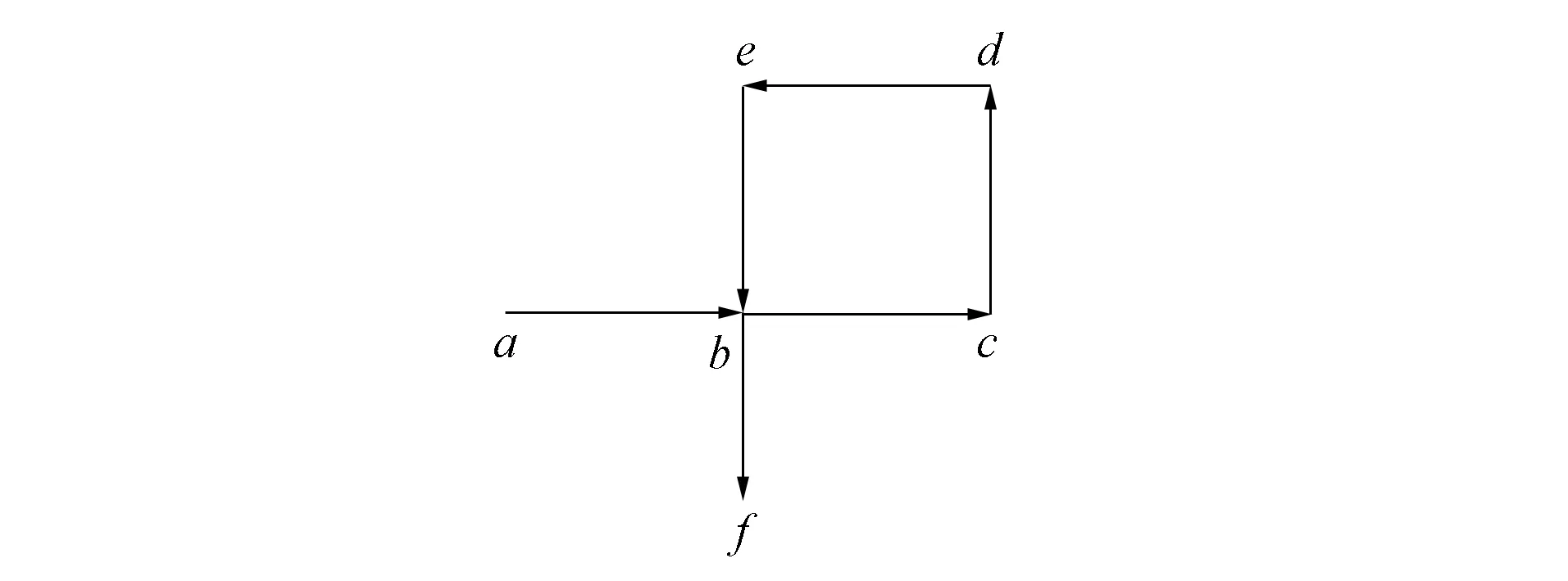
图2 路径中存在环Fig.2 Rings in path

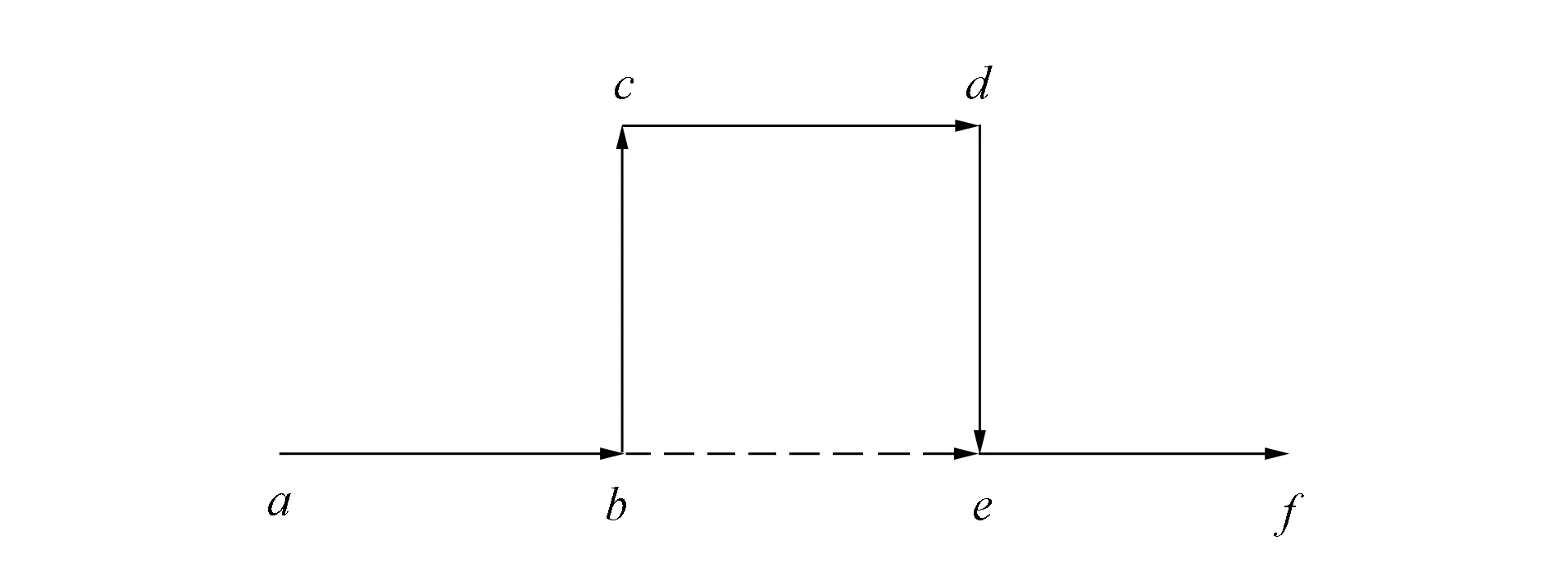
图3 原路径中某子路径可用一条边替换Fig.3 Subpath in original path can be replaced by an edge

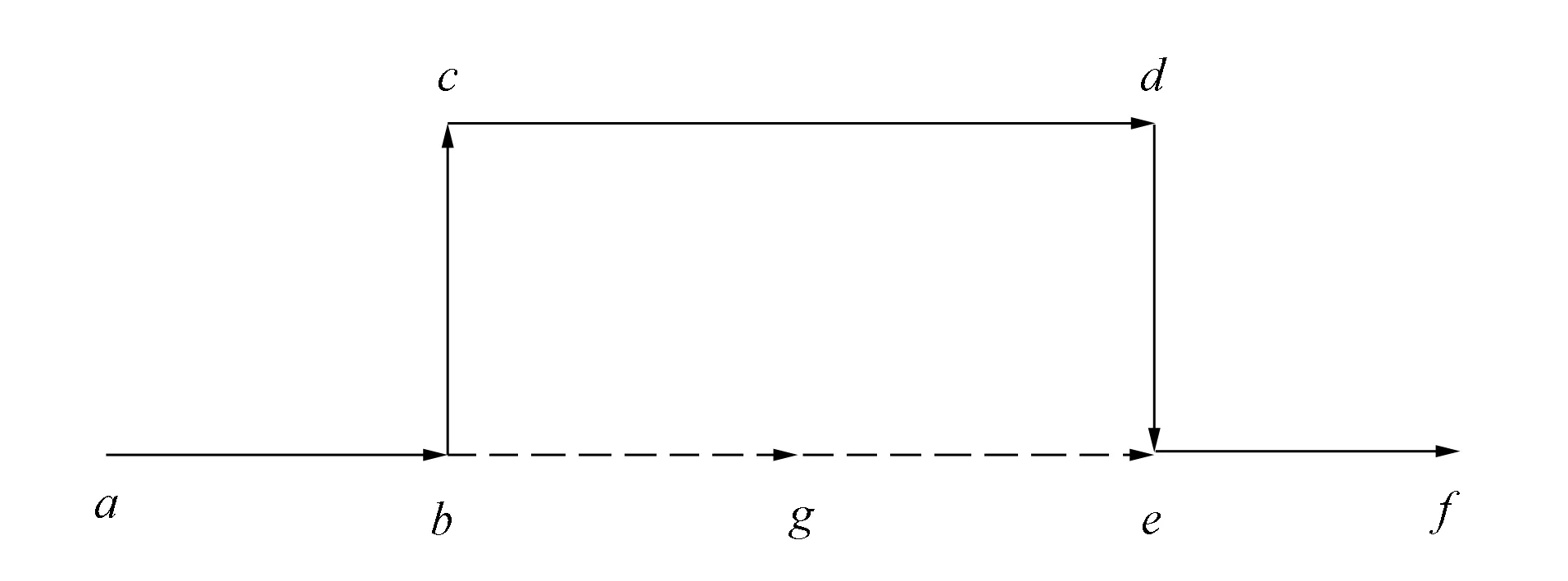
图4 原路径中的子路径可用两条相邻的边替换FIg.4 Subpath in original path can be replaced by two adjacent edges

由图3可见, 当边bc加入路径时记录候选边be和节点e, 当路径加入边ef时检查节点e是否有过记录, 若有根据节点e找到边be, 检查路径abef能否通行, 如果可以, 则可用其替换路径abcdef.由图4可见, 当边bc加入路径时, 记录候选边bg和节点g, 当路径加入边ef时, 遍历驶向节点e的边, 若遍历到边ge是, 则检查节点g是否有过记录, 若有根据节点g找到边bg, 则检查路径abgef能否通行, 如果可以, 则可用其替换路径abcdef.

针对上述3种情形, 对路线选择策略1进行如下改进.从候选列表中选一条将要加入路径的边e, 对当前路径中最后一条边的候选节点j及其候选驶入边做以下判断：

判断1) 候选节点j在路径中是否出现两次以上, 如果是, 则表明该路径存在重复部分, 判断重复部分是否可以删除, 若可以, 则记录删除后的路径通行成本, 并加入候选优化方案中.

判断2) 候选节点j是否在候选边中出现过, 若出现过, 则表明可能存在一条更短子路径, 判断选择该子路径是否违反转弯限制, 如果不违反, 则计算从该子路径通行的成本, 并与原路径通行成本进行比较, 如果优于原路径, 则将其加入候选优化方案中.

判断3) 依次遍历j的候选驶入边, 判断候选驶入边的起始节点是否在候选节点中出现, 若出现, 则表明可能存在一条更短子路路径, 进行与判断2)相同的操作.

当以上判断完成后, 从候选优化方案中选择通行成本最优的方案对路径进行修改, 最后将之前选择的边e加入路径.

3.3 附加数据结构

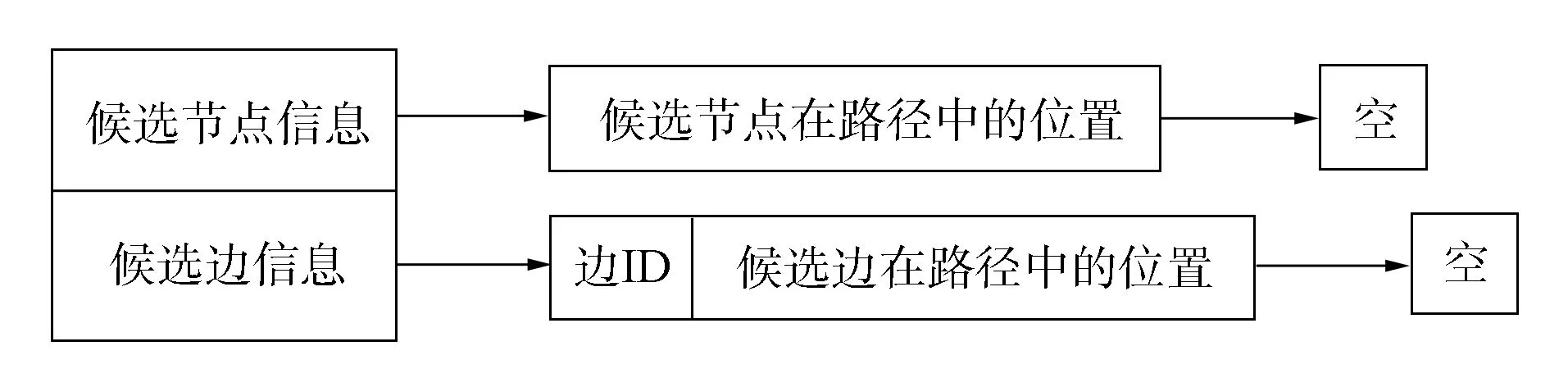
图5 候选节点记录表结构Fig.5 Structure of candidate node record table

为完成上述功能, 本文在原路径基础上添加一张候选节点记录表, 该表采用散列存储结构, 以应对大量的查找需求.为描述方便, 本文将一条边的终点称为候选节点, 例如图2中边ab的候选节点为b, 图3中边be的候选节点为e.而将以某个候选节点为起点, 但未加入路径中的边称为候选边, 例如图3中的边be和图4中的边bg.将驶入某个候选节点但又不属于路径上的边称为候选驶入边.候选节点记录表结构由记录索引和候选节点记录组成, 其中记录表索引为候选节点在路网中的编号.候选节点记录表结构如图5所示.候选节点信息用于记录候选节点是否位于路径上, 由于节点在路径中可能出现多次, 故采用链表结构进行记录.候选边信息用于记录候选节点所在的候选边, 同样由于候选边的个数不唯一, 所以该信息也采用链表记录.

图6为某条搜索到的路径, 其中实线表示路径, 虚线表示候选边.图6中候选节点e和g在候选节点记录表中的记录分别如图7和图8所示.

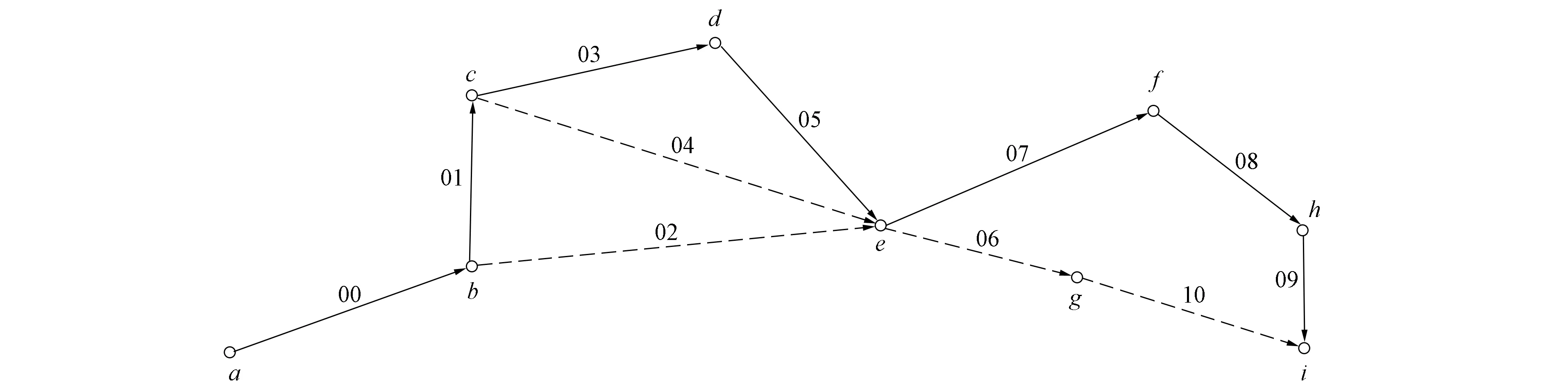
图6 某条搜索到的路径Fig.6 A found path

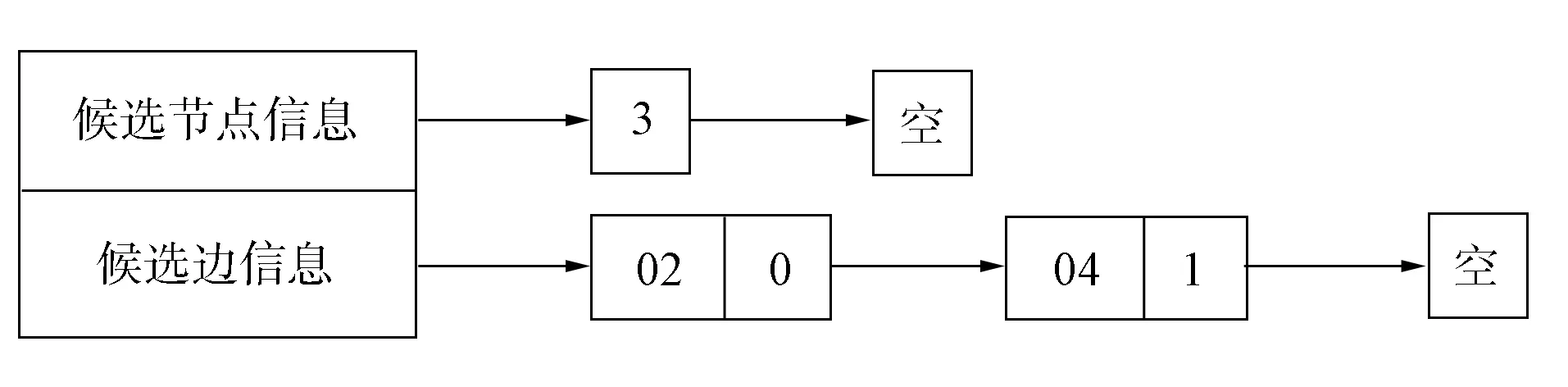
图7 节点e在候选节点记录表中的记录Fig.7 Record of node e in candidate node record table

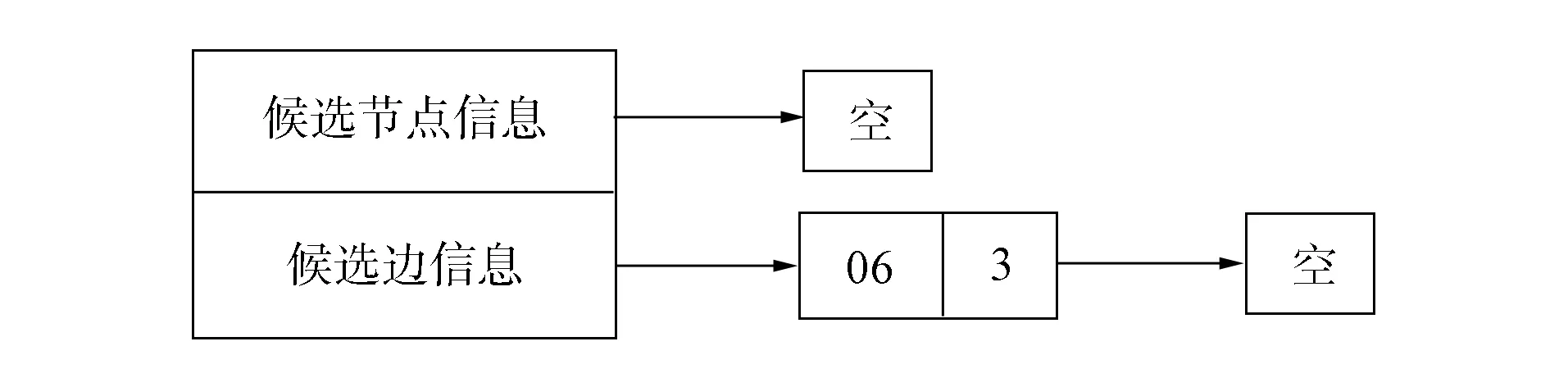
图8 节点g在候选节点记录表中的记录Fig.8 Record of node g in candidate node record table

为方便在删除路径时对记录索引表进行维护, 对路径中的每条边附加一个候选边记录表, 用于存储候选边和候选节点, 如图9所示.图6中边05在候选边记录表中的记录如图10所示.

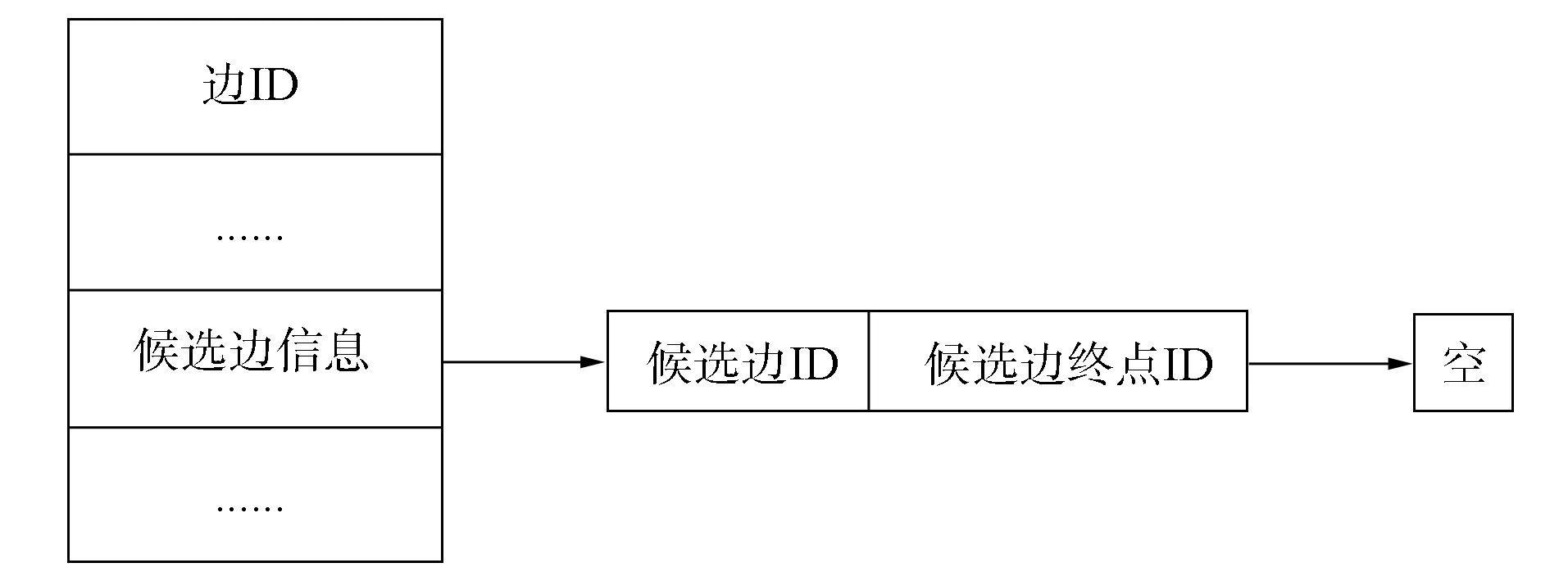
图9 候选边记录表结构Fig.9 Structure of candidate edge record table

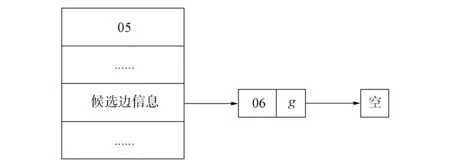
图10 图6中边05在候选边记录表中的记录Fig.10 Record of edge 05 of Fig.6 in candidate edge record table

在增加该数据结构的基础上对原路径选择策略进行如下修改：

步骤1) 初始化最优路径成本为原路径的通行成本;

步骤2) 筛选路径末端的可通行路径, 将满足通行条件的路径加入当前最后一条边的候选边记录表中;

步骤3) 选择一条将要加入路径的边, 并将其从候选边记录表中移除;

步骤4) 筛选路径末端节点的驶入边; 并将驶入边的起始节点ID作为记录索引在候选节点记录表中搜索, 若搜索到记录则表明路径可能存在一条更优子路径;

步骤5) 计算该更优路径的通行成本, 若优于最优路径成本, 则将其替换为该更优路径成本, 同时记录该更短路径;

步骤6) 根据记录的更短路径修改原路径, 同时修改候选节点记录表.

4 实验对比分析

为验证路径选择策略改进方案的有效性, 利用ArcEngine 10.0在JAVA编程环境中进行仿真实现. 实验数据采用ArcGIS提供的美国旧金山交通网络, 该交通网络共有108 226条边, 37 695个节点, 并使用历史流量信息构建了基于行驶时间的成本模型. 实验随机选取一对起始点和终点, 设种群规模为30, 阈值为10, 迭代次数为60, 分别采用两种路径选择策略各计算30次, 两种路径选择策略下算法的收敛性对比如图11所示. 表1列出了一对起始点终止点查找60次的路径平均实验结果.

表1 一对起始点终止点查找60次路径的平均实验结果

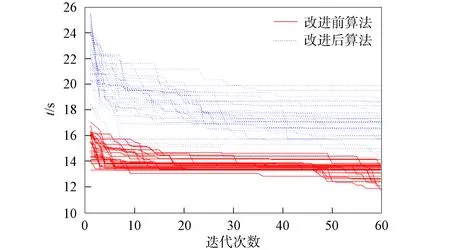
图11 算法改进前后的收敛性对比Fig.11 Convergence comparison of algorithms before and after improvement

由图11和表1可见, 改进后算法的路径选择策略在同等条件下初始化值和最终收敛值均优于改进前算法, 在计算时间上前者略高于后者. 为证明该改进方法具有普遍的适应性, 本文又随机选取了5对起始点和终点进行实验, 结果列于表2.

由表2可见： 1) 在多组实验中, 改进后的路径选择策略表现均优于改进前的策略, 表明该项改进具有普适性； 2) 改进后的路径选择策略使算法在每次迭代的时间花费上比改进前约多50%, 但结果却远优于改进前的策略, 甚至前者初始解的质量已优于后者迭代数十次后得到的解, 因此该项改进可极大减少算法的迭代次数, 从而减少算法的总计算时间.

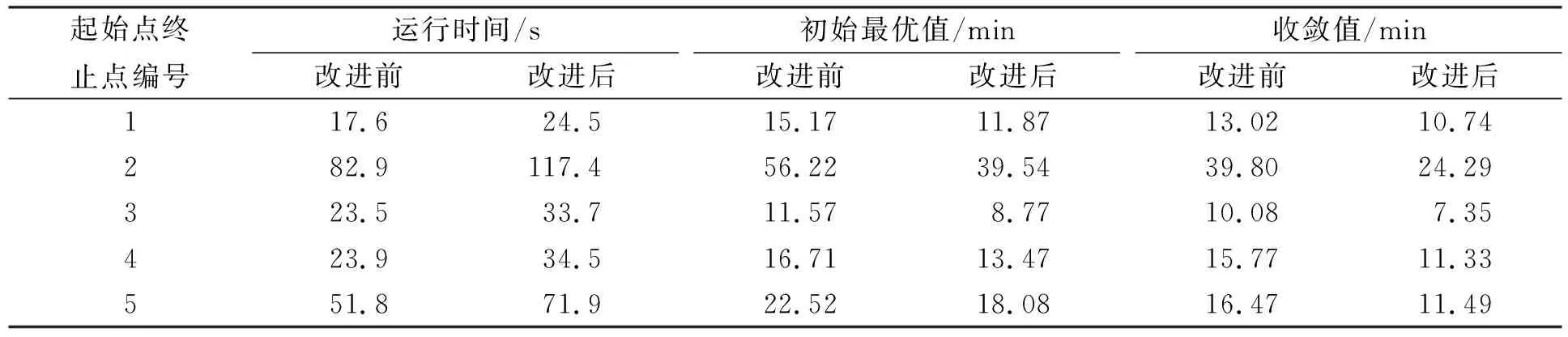
表2 5对起始点终止点分别查找一次路径的实验结果

综上所述, 动态路网是典型的时间依赖网络, 该网络中的最短路径规划问题具有应用价值. 本文利用人工蜂群算法解决时间依赖网络中的最短路径问题, 针对动态路网以出行者为寻优对象时, 可将路网视为FIFO网络这一特性, 对原算法中的个体生成环节进行了改进, 并采用JAVA语言在ArcGIS平台提供的动态路网上进行了仿真实验, 实验结果表明, 该改进策略合理、 有效.