Black-Scholes模型下美式期权定价的神经网络算法

宋海明, 侯 頔

(吉林大学 数学学院, 长春 130012)

0 引 言

期权根据行权时限划分, 可分为欧式期权和美式期权. 欧式期权只能在到期日实施, 美式期权可在到期日前的任意一个交易日实施. 因此关于美式期权定价的研究备受关注. 本文考虑Black-Scholes模型下的美式看跌期权定价问题, 给出一种新的神经网络求解算法. 经典的Black-Scholes模型为

(1)

其中美式看跌期权价格P是依赖于时间t和标定资产价格S的函数,σ,q,r,T和K分别表示标定资产的波动率、 红利、 无风险利率、 到期日和敲定价格,B(t)表示未知的最佳实施边界,Z+=max{0,Z}.

美式期权定价模型(1)是一个自由边界问题, 不存在显式表达式, 因此关于其数值方法的研究备受关注, 目前已取得了许多成果[1-8], 其中最经典的是由Cox等[1]提出的二叉树法, 该方法思路简单、 易实现, 但收敛速度较慢, 且不易推广到高维. Monte Carlo方法[2]因其不依赖维数的优势, 广泛应用于期权定价问题的求解中, 但该方法需要大量的采样才能达到较高的精度, 在实际应用中难以实现.

传统的数值方法通常是针对低维方程设计的, 当维度增加时数值格式设计较困难, 且计算量呈指数增长, 会导致维度灾难.神经网络作为一种机器学习技术, 易实施, 为高维问题的数值求解提供了可能.因此, 本文提出一种新的求解美式期权定价问题的神经网络算法, 并通过与经典的二叉树方法对比说明该算法的优越性.

1 深度神经网络

图1 深度神经网络结构示意图Fig.1 Schematic diagram of architecture of deep neural network

本文针对美式期权定价问题, 设计一种全连接深度神经网络算法(full connected deep neural networks, DNN), 其基本思想是: 利用含有多个未知参数的多层非线性复合函数, 逼近一个映射f:n→m.经典的DNN包含一个输入层、 一个输出层和多个隐藏层, 输入层和输出层的神经元个数由输入和输出值的维度确定.图1为含两个隐藏层的DNN结构, 其中“○”表示神经元, 其将输入向量进行加权求和, 加上偏置项系数后, 再与一个非线性函数复合, 得到输出值.特别地, 给定一个n维向量x作为输入向量, 含有L层隐藏层的DNN可定义为

z(k+1)=σ(W(k)z(k)+b(k)),k=0,1,…,L-1,

(2)

y=W(L)z(L)+b(L),

(3)

其中z(0)=x为输入值,W(k)∈dk+1×dk和b(k)∈dk+1分别为网络的权重和偏置项,dk为第k层的神经元个数,σ表示激活函数.激活函数主要包括Sigmoid函数、 双曲正弦函数和ReLU函数等.定义网络结构后, 基于已知训练集, 可利用优化方法得到未知参数θ={W(k),b(k)}.即根据数据集定义损失函数优化问题为

(4)

通常可采用随机梯度下降法(SGD)和交替方向乘子法(ADMM)等对该优化问题进行求解.

针对期权定价模型(1), 本文将方程组残差函数2-范数的平方和作为损失函数, 通过神经网络求解该优化问题, 得到原方程的近似解.可以证明, 通过该方法求得的解是原方程的唯一解.

定理1若方程组(1)的解在神经网络的逼近空间内, 且足够光滑, 则利用损失优化问题:

(5)

证明： 若P(S,t)是定价模型(1)的解, 且在神经网络逼近空间内, 则对应的损失函数为

2 网络结构

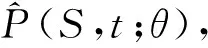
(6)

其中vi(i=1,2,3,4,5)表示相应离散节点的l2范数.

由文献[9]可知, 期权价格在(Kmin{r/q,1},T)处光滑性较差, 故本文利用几何网格提高精度.对任意给定的区间[a,b], 约定其对应n个节点的几何剖分为

(7)

下面给出vi(i=1,2,3,4,5)对应离散点列的取法：

2)v2.在v1搜索过程中, 对于每个固定的tn, 将其停止搜索时对应的后续点列(Sk,tn)(k=m,m+1,…,M)依次加入v2中.

3)v3.固定Smin, 依次选取点(Smin,tn)(n=1,2,…,N).

4)v4.固定T, 依次选取点(Sm,T)(m=1,2,…,M).

5)v5.固定Smax, 依次选取点(Smax,tn)(n=1,2,…,N).

由于v1与v2对应的点列会随每次网络参数的优化更新而变化, 故每次更新网络参数后需都重新选取点列.在对神经网络进行训练时, 先选取N=20,M=40, 当损失函数误差足够小时, 增大M,N为N=50,M=100重新选取训练点进行加细, 并再次进行训练.

3 数值算例

下面对美式看跌期权定价问题(1)进行数值模拟, 以验证神经网络算法的正确性.在方程(1)中, 令σ=0.2,T=1,K=10.r和q按下列3种情形取值:

1)r=0.005,q=0.01; 2)r=0.01,q=0.01; 3)r=0.05,q=0.01.

选取5层全连接神经网络, 单层神经元个数为50.激活函数选取Sigmoid函数.网络的输入变量为(S,t), 输出为期权价格P(S,t).

为验证利用神经网络得到结果的准确性, 本文将其计算初始时刻的期权价格与二叉树方法的结果进行对比, 数值结果如图2所示.由图2可见, 利用神经网络计算的结果与二叉树方法得到的结果吻合, 均大于支付函数, 说明本文提出的算法能较准确地得到美式期权价格.用本文方法得到期权价格的三维图像如图3所示.

图2 不同方法初始时刻美式期权价格的对比Fig.2 Comparison of initial American option price by different methods

图3 期权价格的三维图像Fig.3 Three dimensional images of option price

综上, 本文基于几何网格选点法, 设计了一种针对美式期权定价问题的深度神经网络算法, 并通过与传统的二叉树方法对比, 验证了算法的可靠性.