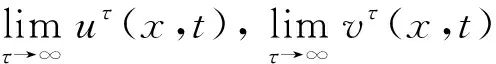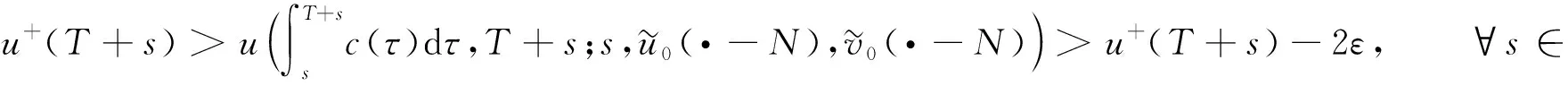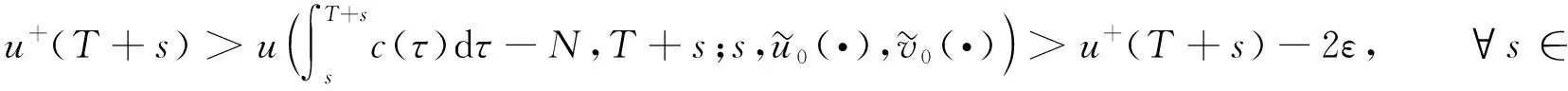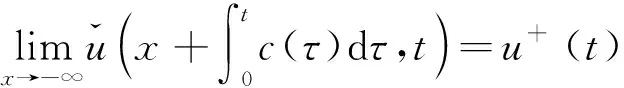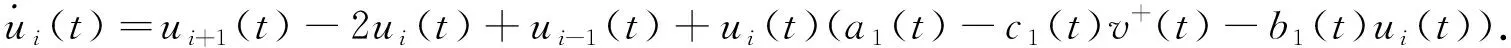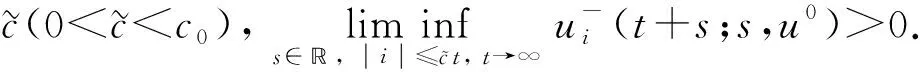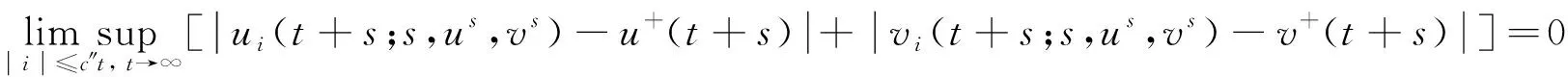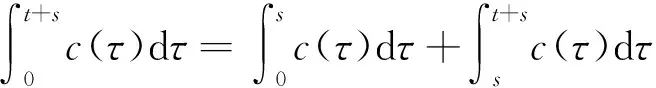时间非均匀介质中两种群竞争格点系统的广义行波
2021-09-22张巧珍
张 巧 珍
(南京航空航天大学 数学系, 南京 210016)
0 引 言
本文考虑下列一般时间非均匀介质中两种群竞争格点系统中广义行波的存在性:

(1)
其中:i∈,t∈; 对任意的t∈,ai(t)∈,bi(t)>0,ci(t)>0, 且ai(t),bi(t),ci(t)(i=1,2)关于t∈是局部Hölder连续的.
系统(1)是下列两种群竞争反应扩散系统的空间离散形式:

(2)
当有机体的运动或内部扩散分别发生在非邻近与邻近的位置之间时, 系统(1)和系统(2)被广泛用于模拟竞争物种的种群动力学[1-4].系统(1)用于竞争物种种群密度进化模型中, 其中有机体内部相互作用或运动发生在非相邻空间位置之间, 用差分算子描述; 系统(2)用于模拟竞争物种种群密度的进化, 其中有机体内部相互作用或运动发生在相邻空间位置之间, 并用微分算子描述.在系统(1)和系统(2)中, 系数a1,a2表示两种群的增长率,b1,c2表示两种群的自我调节能力,b2,c1表示两种群间的竞争能力.空间传播速度和广义行波是系统(1)和系统(2)的中心动力学问题.关于系统(2)在空间和时间齐次介质中[5-14]或者在空间和/或时间周期介质中[15-17]的空间传播速度和广义行波目前已有很多研究成果.文献[18]研究了时间回复下扩散合作/竞争系统的空间传播速度和线性确定性; 文献[19]研究了在一般时间非均匀介质中竞争系统的空间传播速度和广义行波.
关于竞争模型中格点系统的研究目前报道较少: 文献[20-22]研究了时间独立介质中竞争格点系统的空间传播速度和广义行波; 文献[23-27]研究了齐次或周期或时间非均匀介质中KPP(Kolmogorov-Petrovsky-Piskunov)型单一种群格点方程空间的传播速度和广义行波. 本文研究具有一般时间依赖两种群竞争格点系统广义行波的存在性和不存在性, 建立两种群格点系统的比较原理, 并构造系统合适的上下解.
1 基本假设、 概念及主要结果
先给出一些记号及关于系统(1)的假设. 令
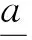
l∞()()={u∈l∞():

对任意给定的(u0,v0)∈l∞()×l∞(), 系统(1)有满足初值条件(u(s;s,u0,v0),v(s;s,u0,v0))=(u0,v0)唯一的(局部)解
(u(t;s,u0,v0),v(t;s,u0,v0))={(ui(t;s,u0,v0),vi(t;s,u0,v0))}i∈.
(3)
注意到, 若u0∈l∞,+(),v0∈l∞,+(), 则(u(t;s,u0,v0),v(t;s,u0,v0))关于所有的t≥s存在, 且u(t;s,u0,v0)∈l∞,+(),v(t;s,u0,v0)∈l∞,+(),t≥s.若系统(1)的一个解(u(t),v(t))={(ui(t),vi(t))}i∈满足对所有的i,j∈, 均有ui(t)=uj(t),vi(t)=vj(t), 则称(u(t),v(t))是空间齐次的.
系统(1)包含以下两个子系统,
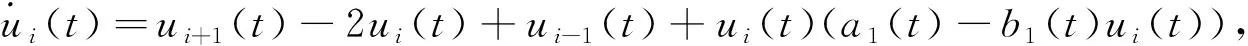
(4)
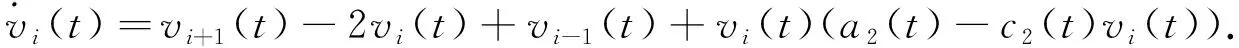
(5)
本文假设:
(H1)表明系统(1)有两个半平凡空间齐次正解(u+(t),0)∈Intl∞,+()×l∞,+() 和(0,v+(t))∈l∞,+()×Intl∞,+(), 其中u+(t)是系统(4)唯一的空间齐次正解,v+(t)是系统(5)唯一的空间齐次正解[23].
(H2) (0,v+(t))在l∞,+()×l∞,+()上是线性不稳定的, 即在l∞,+()×l∞,+()上是线性全局稳定的, 即对任意的(u0,v0)∈l∞,+()×l∞,+()(u0≠0), 当t→∞时,ui(t+s;s,u0,v0)-u+(t+s)→0,vi(t+s;s,u0,v0)→0关于i∈和s∈一致地成立.

在假设(H1)~(H3)下, 一个有趣的中心动力学问题就是研究系统(1)连接(u+(t),0)和(0,v+(t))广义行波的存在性.为解决该问题, 先把系统(1)通过下述变量代换转化为一个合作系统:
进一步将系统(1)转化为
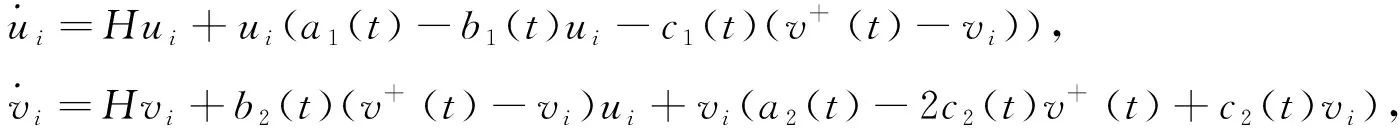
(6)
其中
Hui(t)∶=ui+1(t)-2ui(t)+ui-1(t),i∈,t∈.
显然, 系统(6)在ui(t)≥0和0≤vi(t)≤v+(t)区域内是合作系统, 且系统(1)的平凡解(0,0)转化为(0,v+(t)), 系统(1)的半平凡解(0,v+(t))和(u+(t),0)分别转化为(0,0)和(u+(t),v+(t)).从而研究系统(1)连接(u+(t),0)和(0,v+(t))的广义行波即等价于研究系统(6)连接(u+(t),v+(t))和 (0,0)的广义行波.
将系统(6)满足初值条件(u(s;s,u0,v0),v(s;s,u0,v0))=(u0,v0)∈l∞()×l∞()的解记作(u(t;s,u0,v0),v(t;s,u0,v0))={(ui(t;s,u0,v0),vi(t;s,u0,v0))}i∈.对任意的(u1,u2)∈l∞()×l∞()和(v1,v2)∈l∞()×l∞(), (u1,u2)<(v1,v2)((u1,u2)≤(v1,v2))即为对每一个分量i, 都有ui 定义1(广义行波) 如果存在函数Φ(x,t),Ψ(x,t)(x∈)和c(t), 使得 (7) 假设满足式(7)的(u(t),v(t))={(ui(t),vi(t))}i∈是系统(6)一个广义行波.若对所有的t∈,Φ(x,t)和Ψ(x,t)关于x是非增的, 则称广义行波(u(t),v(t))是单调的.若存在, 使得则称为其下平均速度. 下面给出本文的主要结果: 定理1假设(H1)~(H3)成立, 则有: 2) 当下平均速度小于c0时, 系统(6)不存在广义行波. 首先考虑系统(6)的空间连续形式: (8) 其中u=u(x,t),v=v(x,t),Hu(x,t)∶=u(x+1,t)-2u(x,t)+u(x-1,t),x∈,t∈.令 l∞() 对任意的(u0,v0)∈l∞()×l∞(), (u(t;s,u0,v0),v(t;s,u0,v0))={(ui(t;s,u0,v0),vi(t;s,u0,v0))}i∈是系统(6)满足初值条件(i∈)的解.对任意的(u0,v0)∈l∞()×l∞(), 令(u(x,t;s,u0,v0),v(x,t;s,u0,v0))是系统(8)满足初值条件(u(x,s;s,u0,v0),v(x,s;s,u0,v0))=(u0(x),v0(x))的解.对任意的(u1,u2),(v1,v2)∈l∞()×l∞(), (u1,u2)<(v1,v2)((u1,u2)≤(v1,v2))即为对每个i, 都有ui 令 f(t,u,v)=u(a1(t)-b1(t)u-c1(t)(v+(t)-v)), g(t,u,v)=b2(t)(v+(t)-v)u+v(a2(t)-2c2(t)v+(t)+c2(t)v). 若对任意给定的x∈(x∈),u(x,t)和v(x,t)关于t∈[s,T)是绝对连续的, 且 ut(x,t)≥Hu(x,t)+f(t,u,v),vt(x,t)≥Hv(x,t)+g(t,u,v) 或 ut(x,t)≤Hu(x,t)+f(t,u,v),vt(x,t)≤Hv(x,t)+g(t,u,v) 关于几乎处处的t∈[s,T)成立, 则在×[s,T)上关于t连续的一组函数(u(x,t),v(x,t))称为系统(8)(系统(6))的一个上解或者下解.有限个上(下)解的下确界(上确界), 称为该系统的一个广义上(下)解. 下面建立系统(8)解的比较原理, 关于系统(6)解的比较原理类似可证. 命题1(比较原理) 假设(u2(x,t),v2(x,t))和(u1(x,t),v1(x,t))分别是系统(8)在[s,T)上的有界上解和下解, 且(ui(x,t),vi(x,t))∈[0,u+(t)]×[0,v+(t)](i=1,2)关于x∈,t∈[s,T]成立.若(u1(·,s),v1(·,s))≤(u2(·,s),v2(·,s)), 则(u1(·,t),v1(·,t))≤(u2(·,t),v2(·,t))关于t∈[s,T)成立. 证明: 令 w1(x,t)=ect(u2(x,t)-u1(x,t)),w2(x,t)=ect(v2(x,t)-v1(x,t)), 其中c待定.对任意给定的x∈, [s,T]上存在一个Lebesgue测度为0的可测子集E, 使得 (9) 关于t∈[s,T]E成立, 其中 因为系统(8)在[0,u+(t)]×[0,v+(t)]上是合作的, 则b1(x,t)≥0,a2(x,t)≥0.由ui(x,t)和vi(x,t)(i=1,2)的有界性知, 存在一个c>0, 使得b2(x,t)≥0和a1(x,t)≥0成立. 断言wi(x,t)≥0(i=1,2)关于x∈,t∈[s,T]成立.令下面只需证明关于x∈,t∈[s,T0], 该断言成立即可, 其中,使得或则存在t0∈(s,T0), 使得 因为w1(xn,s)≥0, 从而 令n→∞, 则 矛盾.因此wi(x,t)≥0(i=1,2)关于x∈,t∈[s,T]成立, 从而(u1(x,t),v1(x,t))≤(u2(x,t),v2(x,t))关于x∈,t∈[s,T]成立. 命题2假设(un,vn)∈l∞,+()×l∞,+()(n=1,2,…), (u0,v0)∈l∞,+()×l∞,+(), 且{‖un‖},{‖vn‖}是有界的.若当n→∞时, (un(x),vn(x))→(u0(x),v0(x))关于x在有界集上一致地成立, 则当n→∞时, 对每个t>0, 都有(u(x,t+s;s,un,vn),v(x,t+s;s,un,vn))→(u(x,t+s;s,u0,v0),v(x,t+s;s,u0,v0))关于x在有界集和s∈上一致地成立. 证明: 令 un(x,t+s;s)=u(x,t+s;s,un,vn)-u(x,t+s;s,u0,v0), vn(x,t+s;s)=v(x,t+s;s,un,vn)-v(x,t+s;s,u0,v0), 则 其中 取λ>0, 令 X(λ)={(u,v):→2: (u(·)e-λ|·|,v(·)e-λ|·|)∈l∞()×l∞()}, 进而 由Gronwall不等式, 可得 ‖(un(·,t+s;s),vn(·,t+s;s))‖X(λ)≤e(α+M2)tM‖(un(·,s;s),vn(·,s;s))‖X(λ). 又因为当n→∞ 时, ‖(un(·,s;s),vn(·,s;s))‖X(λ)→0关于s∈一致地成立, 因此当n→∞时, (un(x,t+s;s),vn(x,t+s;s))→(0,0)关于x在有界集和s∈上一致地成立.证毕. 引理1令a(t)∈C(,(0,∞)), 则 引理1的证明可参见文献[28]. 引理2令(u0,v0)∈l∞,+()×l∞,+(), 若存在一个常数使得 (10) 关于s∈一致地成立. (11) |uin(tn+sn;sn,u0,v0)-u+(tn+sn)|+|vin(tn+sn;sn,u0,v0)-v+(tn+sn)|≥ε0 (12) 成立. (13) 关于所有的i∈,s∈,成立; (14) 关于任意的i∈,s∈,成立.注意到当n→∞时,因此存在 (15) 注意到 由比较原理, 可知 关于任意的i∈,t>0和n≥N成立, 其中由的定义可知关于i∈局部一致地成立.因此, 由命题2知, 对每个t>0, 均有 (18) 关于i∈局部一致地成立.由式(13),(16)~(18)可知 关于n≫1成立.由式(14), 有 uin(tn+sn;sn,u0,v0) 关于n≫1成立, 则 |uin(tn+sn;sn,u0,v0)-u+(tn+sn)|+|vin(tn+sn;sn,u0,v0)-v+(tn+sn)|<ε0 关于n≫1成立, 与式(12)矛盾.因此式(10)成立.证毕. 由假设(H3)可知, 下列方程存在一个严格的正解h(t): 记c(t,μ)=(e-μ+eμ-2+a1(t)-c1(t)v+(t))/μ.下面构造系统(8)合适的广义上下解. 关于x∈,t∈成立, 从而有 关于x∈,t∈成立. 令 因此, 令 则可得 关于所有的x∈,t≥s,s∈成立.从而满足引理3中3). 满足 (19) 关于所有的t∈(tk,tk+1),k∈成立. 固定上述δ>0和A(t), 令 其中d>1待定.则有 又由c(t,μ)=(e-μ+eμ-2+a1(t)-c1(t)v+(t))/μ, 可得 关于t∈(tk,tk+1)成立.再注意到 类似证明式(20)的结论, 可得 关于t∈(tk,tk+1)成立.令 定义 关于x∈,t≥s成立. 下面证明定理1. 由引理3可得 uτ2(x,t)≤uτ1(x,t), ∀x∈,t>-τ1, vτ2(x,t)≤vτ1(x,t), ∀x∈,t>-τ1. 断言 (23) 关于t∈一致地成立.事实上, 令由及式(22)和可得 令(u0(x),v0(x))恒为(u0,v0), 其中 关于s∈和x∈一致地成立.因此对任意的ε>0, 存在T∶=T(ε)>0, 使得 u+(T+s)>u(x,T+s;s,u0,v0)>u+(T+s)-ε, ∀s∈,x∈. 从而由c(t)的定义可知 关于所有的s∈和x∈成立.由命题2知, 存在N∶=N(ε)>1, 使得 即 注意到 则可得 则有 关于t∈一致地成立. 2) 令 关于s∈一致地成立, 其中 断言c*=c0.事实上, 考虑 (24) 对任意的u0∈l∞,+(), 令u-(t+s;s,u0)是式(24)满足u-(s;s,u0)=u0的解.由比较原理知, 对任意的(u0,v0)∈l∞,+()×l∞,+(), 有 (25) 关于s∈一致地成立.从而可得c*≥c0. (26) 关于s∈一致地成立. ui(t+s;s,u0,v0)≤ui(t+s;s,us,vs),vi(t+s;s,u0,v0)≤vi(t+s;s,us,vs) 关于i∈,s∈和t≥0成立.联合式(26)可推出 (27) 关于s∈一致地成立.再注意到由定理1中1)可得 则 关于s∈一致地成立.由式(27)和式(28)可得矛盾.因此c*=c0. 假设满足式(7)的(u(t),v(t))={(ui(t),vi(t))}i∈是系统(6)连接(u+(t),v+(t))和(0,0)的广义行波.下面证明其下平均速度注意到关于所有的z∈成立.因此, 可选取(), 使得(u0,v0)≤(Φ(x,s),Ψ(x,s))关于所有的s∈成立.令0<ε≪1, 则由c*=c0和比较原理, 有

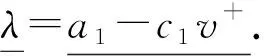

2 比较原理及上下解的构造
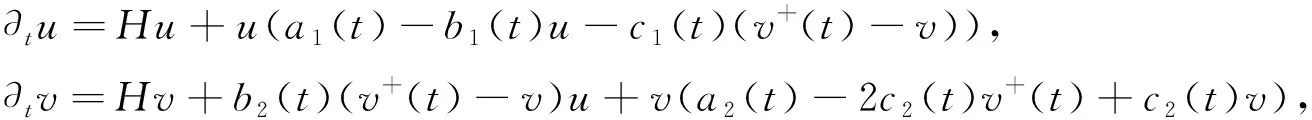
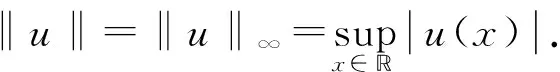
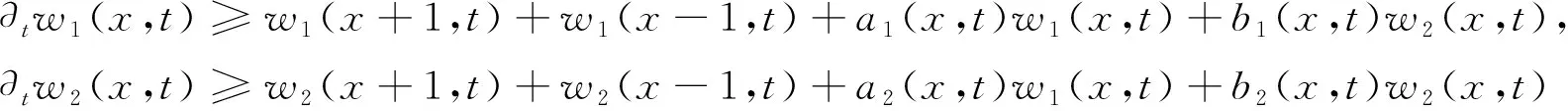
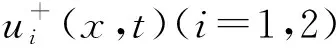
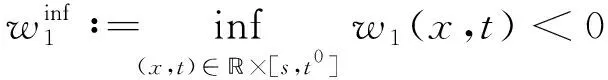
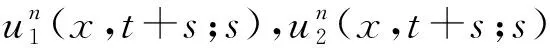


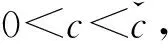
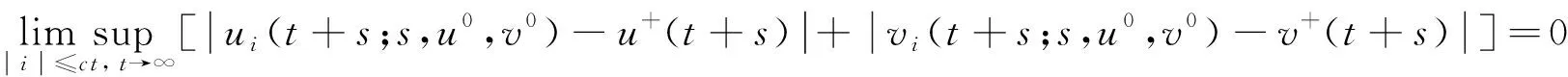

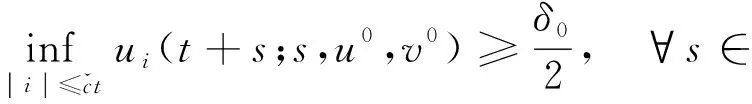

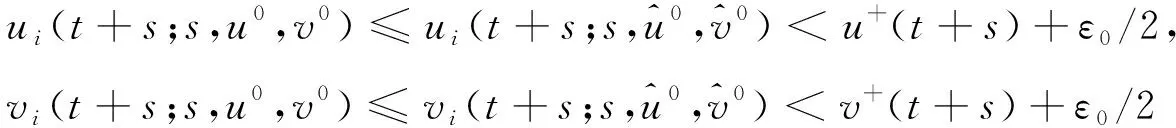
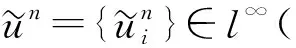

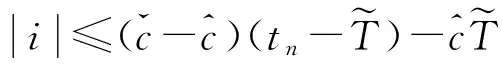


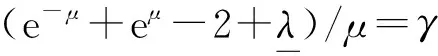
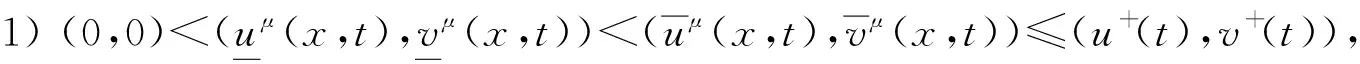
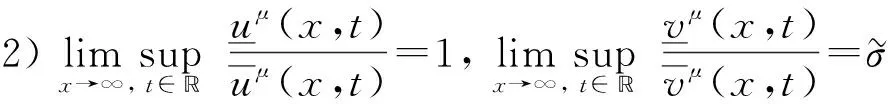
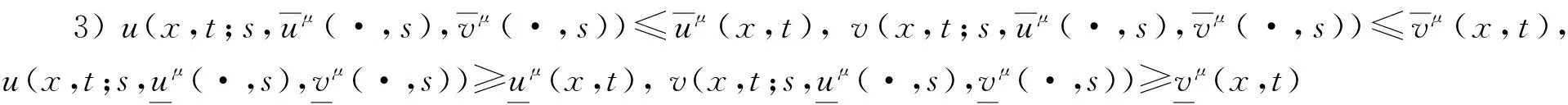
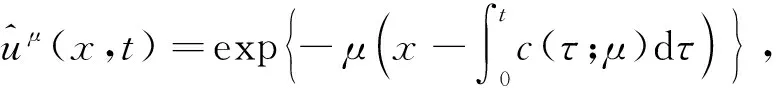



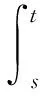

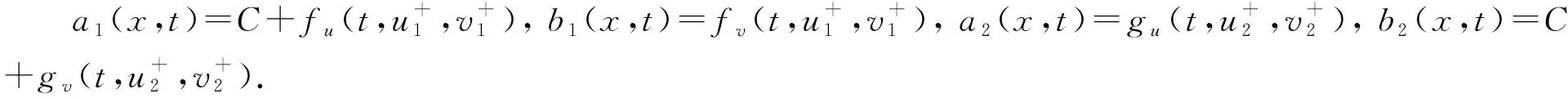
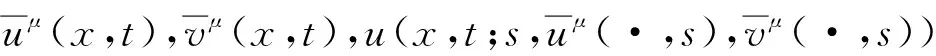
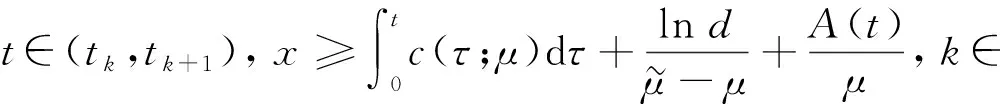

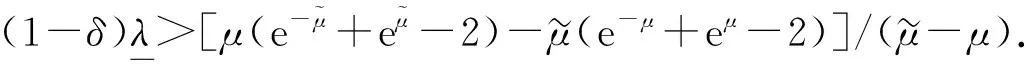





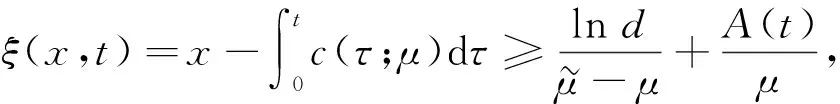
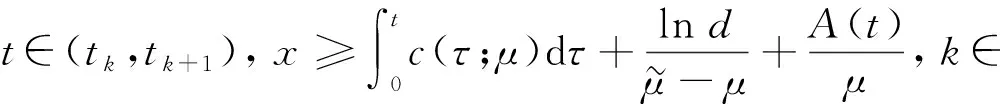


3 广义行波的存在性