强化学习在资源优化领域的应用
2021-09-22王金予魏欣然石文磊张佳
王金予,魏欣然,石文磊,张佳
微软亚洲研究院,北京 100080
1 引言
资源优化关心如何更有效地管理与利用资源以提高整体的收益。资源优化问题无处不在,大到国与国之间的贸易往来,小到每个人的衣食住行,整个人类的经济、生产、生活活动都是围绕着资源运行的。一直以来,传统的运筹学方法,如组合优化、线性规划、非凸优化等技术被广泛地应用于海运优化[1-4]、出租车派单[5-6]、供应链管理[7-9]、货物装箱[10-11]等资源优化场景,并且成果斐然。
虽然基于运筹学的方法对解决上述资源优化问题提供了很大帮助,但实际中仍然存在的很多挑战严重地降低了运筹学方法的求解效果。这些挑战主要来自以下3个方面。
● 求解空间非常巨大。很多实际场景涉及的资源节点众多、依赖关系复杂、待求解周期长,导致构造的运筹学模型动辄几十万变量、上百万约束,使得求解速度缓慢、计算成本高昂,造成运筹学模型很难应用于一些时效性要求高的场景,如出租车派单。
● 不确定性强。资源优化问题通常是针对未来的情况的,例如海运公司需要根据未来的供需情况进行集装箱的平衡调度,出租车派单中需要根据未来的订单情况进行匹配,供应链中需要考虑未来各环节的产能与仓储能力以及最终的客户需求进而决定供给方案。在这种情况下使用基于运筹学的方式进行求解就需要对未来的情况进行显式的预测,并且基于这些预测建立模型。但是预测的精度总是有限的,尤其需要较长时间的预测时,准确度更加难以保证。这就导致求解质量不高、优化效率低,甚至得到的解无法执行。
● 场景逻辑复杂、多变。在实际问题中,由于业务逻辑复杂,存在很多用运筹学中的约束无法有效刻画的逻辑,如跨国贸易中的一些政策、法规要求,供应链中未满足客户需求而产生的名誉、客户流失等潜在成本。在这种情况下,运筹模型的建立需要进行人工设计,近似地刻画这些约束,这不可避免地使模型具备了主观性。与此同时,场景的业务逻辑(如业务模式、法规要求等)会随时间发生改变,一旦发生变化,又需要大量的人力重新调整模型以适应新的变化,导致人工成本高昂,而且模型的稳定性难以保证。
上述挑战超出了传统运筹学方法的范畴,需要引入全新的解决方案。事实上,随着信息技术的不断发展以及存储设备的价格越来越低,各行各业积累了大量的历史数据,如海运领域的航线变化、船舶离港到港事件、供需关系数据,出租车领域的车辆轨迹、订单需求数据,快递领域的包裹尺寸、目的地分布数据等。这些宝贵的数据中包含了业务的复杂变化与各种事件的不确定性,隐式地体现了问题的运行逻辑。如何充分地利用这些数据,从中发现规律、学习策略是解决资源优化问题面临的重要挑战,也是重大机遇。显然,这些数据在传统的运筹学方法中很难发挥出最大价值。
随着强化学习在围棋[12]、游戏[13]等序列化决策领域大放异彩、在多智能体协作等领域取得较好表现[14],它的一些优秀特性也得到了资源优化领域的关注。首先,基于强化学习的解决方案决策非常高效。虽然强化学习策略的训练非常耗时,但是这些训练工作可以离线进行,实际中只需要利用训练好的模型进行推理,因而在绝大部分情况下可以做到近似实时决策。其次,使用强化学习的方法并不需要显式地对未来进行预测,模型可以从交互经验、海量数据中发现规律、学习策略,从而帮助做出合适的决策。最后,在强化学习中,模型不需要对业务逻辑进行建模,可以完全把业务逻辑当成一个黑盒,避免了对复杂业务逻辑的刻画工作和刻画主观性问题。当业务环境发生变化时,智能体能够及时地利用数据中蕴含的变化信号,从而更加迅速和敏锐地通过与业务环境的交互重新找到合适的优化方案。鉴于这些特点,近年来强化学习算法结合行业大数据的解决方案在资源优化领域得到越来越多的应用,并取得了一系列优秀的成果。
基于这种行业趋势,本文针对强化学习算法在资源优化领域的应用展开调研,帮助读者了解该领域最新的进展,学习如何利用数据驱动的方式解决资源优化问题。鉴于资源优化问题场景众多、设定繁杂,划分出3类应用广泛的资源优化问题,即资源平衡问题、资源分配问题、装箱问题,集中进行调研。在每个领域阐述问题的特性,并根据具体的问题特性进行细分,然后以场景为中心进行具体工作的阐述,并重点从问题的建模、特征设计、奖励设计、策略学习等方面展开具体介绍。
2 基本知识
2.1 强化学习的基本概念
强化学习以马尔可夫决策过程(Markov decision process,MDP)为基础构造模型[15]。一个典型的马尔可夫决策过程可以表示为五元组分别表示状态空间、动作空间、状态转换概率函数、奖励方程和衰减因子。状态空间,表示当前环境的全部状态的集合;动作空间,表示当前环境中各个状态下可采取的动作集合,特别地,对于一个给定的状态s,有效的动作空间表示为,且有;状态转换概率函 数描述了在状态s下采取动作a,环境跳转到状态s′的概率;奖励方程R可以定义为表示在状态s下完成动作a后从环境中得到的奖励;衰减因子γ用来对长期奖励进行建模,用于描述每个动作a的作用效果随时间推移的衰减程度,即环境给的单步奖励rt+1对前序动作at的衰减程度,奖励接收时间与动作执行时间离得越远,衰减程度越大。
强化学习中的两大主体分别是智能体和环境。强化学习智能体通过不断地与环境进行交互来收集经验,并从经验中进行学习。对于一个给定的状态s,智能体采取动作a后,环境将跳转到下一个状态s′,并返回一个奖励r,这样就得到了一条经验数据。智能体与环境交互过程中的全部状态、动作序列共同构成了此次交互的一条轨迹。一条轨迹对应的全部奖励值之和被称为这条轨迹对应的回报值,用表示,
2.2 强化学习算法基础
根据智能体在与环境交互过程中具体学习的内容,可以把无须对环境进行建模(即model-free)的强化学习算法分为两大类:直接学习动作执行策略的策略优化算法(如REINFORCE[16])和通过学习一个值函数进而做出动作执行决策的值优化算法(如Q-learning[17])。
在策略优化这类算法中,主要学习对象是动作执行策略πθ,其中,θ表示当前策略的全部参数。策略πθ负责完成从状态s到动作a的映射,具体分为确定性策略和随机性策略。确定性策略将给定的状态s映射到确定的动作a,即;对于给定的状态s,随机性策略将给出动作a的概率 分布,即。朴素 的REINFORCE算法又被称为朴素的策略梯度(vanilla policy gradient,VPG)算法,是一种随机性策略算法,更新的规则是以梯度上升的方式更新参数θ,从而提升与环境交互所获得的轨迹的对应回报值,即策略更新的目标函数为:
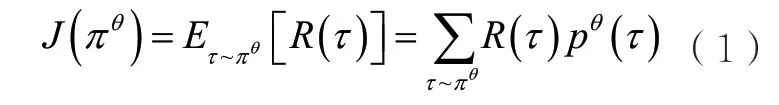
进一步可以得到对应的梯度:
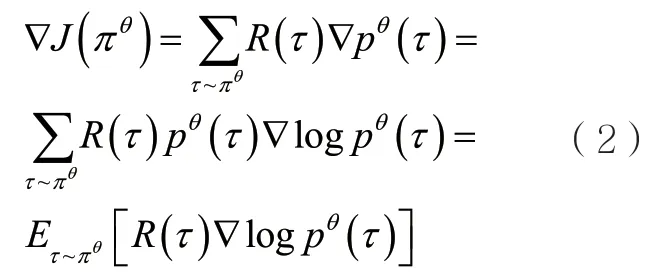
从而可以通过抽取一定量的经验数据实现策略的更新梯度计算,这里把抽取的经验数据的数量定为N:

除了REINFORCE算法,策略优化算法还包括信赖域策略优化(trust region policy optimization,TRPO)算法[18]、近端策略优化(proximal policy optimization,PPO)算法[19-20]、优势动作评价(advanced actor-critic,A2C)算法[21]、异步优势动作评价(asynchronous advantage actorcritic,A3C)算法[21]等。
值优化算法的典型代表是深度Q网络(deep Q network,DQN)[13],DQN主要学习的是一个动作-价值函数类似地,这里的θ指的是当前动作-价值函数的全部参数,而则表示基于参数θ,在状态s下采取动作a对应的价值的估计值,也可以理解为在状态s下采取动作a后仍基于参数θ与环境交互、预计能从环境中获得的所有奖励值的和的期望。最终,依据动作-价值函数,根据值最大化的原则,DQN算法选取的动作是。当智能体与环境进行交互并收集到一定数量的经验数据后,即得到状态s与状态s′之间实际相差的奖励值r后,考虑到Q函数应当具备的自洽性,可以根据最小化与的估计误差的原则来更新动作-价值函数,则损失函数为:
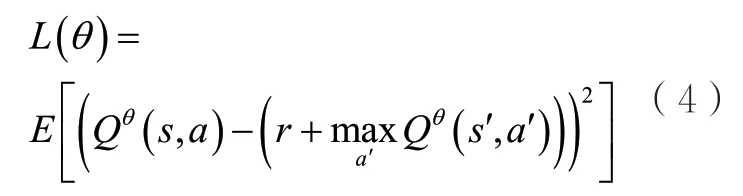
3 资源平衡问题
资源平衡问题指研究资源有限系统中分散资源点间的资源调度策略,以优化资源需求与资源消耗在时空分布上的一致性。根据平衡问题的触发与作用机制的不同,资源平衡问题可以划分为被动平衡问题、主动平衡问题和基于市场机制的平衡问题。
3.1 被动平衡问题
现实场景中的资源平衡问题往往会受到诸多现实因素的制约,如路线、成本等,因此调度策略往往需要遵循现实世界的既定规则,即调度动作只能由现实事件触发。以交通场景为例,触发事件可以是负责运载资源的交通工具抵达资源点。在固定路线的约束下,典型的资源网络可以定义为G=(P,R,V),其中,P、R、V分别表示资源点、交通路线、交通工具的集合。每个端点Pi∈P表示一个资源点,将Pi处的初始库存资源表示为,用和分别表示不同时刻的库存数量、资源需求数量和资源供应数量。每条路线Ri∈R表示物流网络中的一条通路,由一系列连续的资 源点组成,表示这条路线上的资源点总数。每条路线Ri上都有一队固定的车辆,且每一辆运载工具Vj∈VRi都有其固定的运行时刻表及容量上限Cj,同时,不同的路线之间可能在任意资源点相交。当运载工具到达资源点时,它可以从资源点装载资源,也可以向资源点卸载资源。空集装箱重定位就是比较典型的被动平衡场景,下面将对这一场景的相关算法进行介绍。
空集装箱重定位问题:空集装箱是航运中用来装载货物的核心资源,而世界各国和地区之间的进出口贸易存在很大的贸易不对等,这导致空集装箱的供需极度不平衡。空集装箱重定位问题是在运输货物的同时合理运输适量的空集装箱,以达到优化货物运输效率的目标。作为交通网络中的资源平衡问题,这一问题受到了运筹优化领域的广泛关注[1-4]。
1997年,Crainic T G等人[1]总结了在货运运输规划和执行中的主要问题,并以计算机技术为基础,提出了相应的策略模型和方法。随后,Epstein R等人[2]针对空集装箱重定位问题进行了更加细致的研究,设计了物流优化系统来管理资源不平衡的问题,并提出了基于供需预测和库存控制的多商品网络流量模型。参考文献[22]将环境的不确定性引入空集装箱重定位系统中,建立了一个针对随机供需、随机船舶容量的两阶段随机规划模型,得到了良好的效果。Song D P等人[23]对基于运筹学的资源平衡解决方案进行了详细的回顾,这些方法通常是多阶段的,即先预测每个资源点未来的供需情况,再采用组合优化的方法求解每个资源点的最优策略,最后通过裁剪模型输出的原始策略来生成可行解。然而,上述传统的运筹学方法受限于供需的不确定性、复杂的非凸业务约束以及交通网络的高度复杂性,难以在真实场景中得到令人满意的调度策略。
为了解决上述挑战,Li X H等人[24]将这一问题建模为一个由事件驱动的多智能体强化学习问题。具体地,每条船对应一个智能体,当船舶Vi到达港口Pj时,会触发相应的智能体做出决策,且其动作空间表示将部分资源从车上卸下,时则相反。同时,这些操作始终受到船舶的容量Ci的限制。在状态S和奖励函数R的设计上,研究根据各智能体间合作范围的不同,提出自我意识、领土意识和外交意识3种模式。在自我意识中,智能体是自私且短视的,因此状态SI可以仅由当前船只和当前港口的特征来描述,即,而奖励函数rI是只与当前船只的库存与空箱短缺数量相关的函数。领土意识则具有更广阔的视野,它关注当前船只Vi即将路过的多个港口,以及当前港口Pj的后续接驳的多个船只,此时状态可以表示为,这一模式使得智能体可以基于航线的信息做出更全面的决策。进一步地,外交意识在领土意识的状态ST上增加了当前港口Pj所在的所有路线的信息,其奖励函数表示为,其中,α表示自我奖励rI的权重,即外交奖励是自我奖励rI与相邻路线的奖励rc的加权均值,从而实现智能体与交叉航线的合作,使得资源可以在航线间进行再平衡。此外,将船只作为智能体,是考虑到沿着同一路线行驶的多个船只通常共享相似的环境,因此它们可以共享相同的策略,从而显著降低模型的复杂度。同时,船只的航行过程也是其信息视野的自然放大过程,因此将其作为智能体能够获得更好的全局策略。
本质上,合作多智能体系统通过对多个分散智能体求取全局最优解,建模智能体间的合作行为。因此,在实际问题中,要想建模智能体与环境实体之间复杂的协作关系,要充分了解每个智能体及与它相关的智能体和环境实体的状态信息。为此,Jiang J C等人[25]提出了使用交互图对整个环境进行建模的方法。其中,顶点表示智能体或环境实体,当两个顶点相互作用时,便存在边。这一研究方法在多智能体强化学习(multi-agent reinforcement learning,MARL)框架下,利用图神经网络(graph neural network,GNN)在连通的智能体间传递合作信号,并在各种小游戏中取得了不错的表现。但是,现实场景往往要比游戏更复杂。简单的GNN模型通常使用比较简单的池函数作为聚合函数,并在信息传播的过程中始终假设交互图中的所有顶点是同构的。然而,实际问题中的顶点大多是异构的,异构顶点之间不同的特征空间阻碍了有效的信息传递。同时,简单的聚合函数也可能造成信息的丢失或过平滑问题。
因此,Shi W L等人[26]提出了一种新的合作策略学习框架,使用预训练的方法学习异构的表征,并在真实场景上的大量实验中证明了其优越性。该方法将多智能体系统表示为一个异构的交互图,并提出了一种新的多智能体强化学习框架。框架由两部分组成:基于编码器-解码器的图注意模块(EncGAT)和使用actor-critic的预训练流程(PreLAC)。其中,EncGAT模型学习交互图中的信息表示,然后将这些信息输入actor-critic网络中,以帮助它学习到更好的合作策略。然而,在A2C算法中引入EncGAT模型后,这一复杂结构会使得多智能体系统的学习过程变得更加困难。为了提高学习效率和学习策略的有效性,研究人员首先使用局部奖励训练EncGAT模型,得到多个执行自私策略的actor和critic,即它们都只关心自己获得的局部奖励是否最大;然后使用预先训练好的EncGAT网络参数初始化actor和critic;最后使用全局的奖励函数进行微调。
3.2 主动平衡问题
不同于被动平衡问题,在主动平衡问题中,资源调度的动作成本往往不高,且存在专用于资源调度的运输工具可供调配,因此调度动作可以由资源点根据自身情况主动、灵活地触发,不再受限于环境事件。
以基于人工的共享自行车重定位为例进行说明。近年来,作为连接城市“最后一公里”的解决方案,共享自行车系统为人们提供了新式的公共交通工具。同样地,由于自行车使用在空间和时间领域的不平衡,在共享自行车的站点可能出现车辆堆积和车辆不足的情况。由于共享自行车站点往往数量庞大、路线庞杂,对共享自行车系统的研究不仅集中在自行车重定位策略上,同时也涉及系统设计、供需预测、行程建议等多个方面。自行车的重定位方法一般被分为基于人工的重定位方法[27-33]和基于用户的重定位方法[34-38]。
基于人工的重定位方法使用多辆三轮车在车站周围移动,在不同的车站间装卸自行车。与空集装箱重定位不同的是,由于自行车重定位场景的站点较多且分布密集,三轮车不设置固定路线,而是根据车站的调度需求进行随机移动。重定位可以以静态或动态的方式进行,静态重定位指当系统不运行或在夜间时,工作人员将自行车重新按需分配到系统中。这一问题的解决方案大多基于优化模型[23],并将最小化总行程作为优化的目标。动态重定位问题[28-40]也采用优化模型,但模型往往过于复杂,无法建模策略的长期影响并应对真实环境中存在的诸多不确定性。
为了解决这一问题,Li Y X等人[31]提出了一种基于时空注意力的强化学习模型。为了更好地定义这一问题,并降低大规模共享自行车系统内的问题复杂性,他们提出了一种名为IIIB的两步聚类算法。上述聚类算法首先根据某一时段内站点的空间聚集程度和轨迹分布将其划分为不同的区域,再将各个区域聚类成内部平衡且相互独立的簇。簇Ci内部各区域sj间的平衡性可以表示为,Ci和Cj之间的独立性定义为,其中o、r分别表示借、还的车数,f表示区域和间的轨迹。该方法将每个卡车作为一个智能体,为每个区域分配一定数量的卡车,它们在区域内部不断地更新目的地,完成自行车重定位任务。观测状态S由一个2ni+1维的向量表示,包含系统状态(容量、供需等)、其他卡车状态(目的地和卸载量)和当前车站的状态,ni表示当前簇中的区域数量。智能体的动作由一个ni维的one-hot向量和1位表示卸载量的数字表示。基于以上设定,上述研究设计了一个时空强化学习模型,使用深度神经网络估计其值函数,为每个区域训练其重定位策略,并在训练中巧妙地通过剪枝规则进一步降低模型的训练复杂度。
3.3 基于市场机制的平衡问题
基于市场机制的平衡问题指不使用运输工具或调度工具直接在资源点间转移资源,而使用定价、奖惩等机制来影响系统中的供需情况或运行机制,从而间接提高资源需求与资源消耗在时空分布上的一致性。
以基于用户的共享自行车重定位为例进行说明。以人工为基础的定位方法利用多辆卡车或自行车拖车,通过在不同区域装卸自行车实现重新定位。然而,其再平衡效果在很大程度上取决于需求预测的准确性。此外,由于运输工具的行程、维护、人工成本较高,基于人工的方法往往需要大量的预算。相比之下,以用户为基础的方式通过向用户发放折扣、奖励的途径,鼓励用户选择特定的取车或落车地点,是一种更加经济和灵活的重新平衡系统的方式。
Contardo C等人[27]首次提出了动态的公共自行车共享平衡问题,对这一问题进行了详细的定义,从运筹学角度给出了这一问题在中大型系统中的解决方案,并将定价策略作为平衡系统中的一个子问题。随后,Chemla D等人[34]提出了一种定价策略,使得不依赖人工移动自行车的平衡策略成为可能。该方法依据现实经验将空间分为多个独立区域,在真实用户的行为基础上开发了多功能模拟器,并在其上对定价策略进行了实验。进一步地,Singla A等人[37]提出了一种众包机制,通过现金奖励的方式激励用户在特定的区域取车或换车,从而实现自行车的重定位。他们模拟了用户进行自行车租赁的完整过程,并为之设计了一个完整的激励体系,通过用户模型评估是否为用户提供建议路线和相应的奖励,同时采用动态定价机制,在给定的预算约束下,实现自行车使用效率的最大化。他们在模拟器上验证了该方法的性能,并首次将动态激励系统的自行车重定位系统部署在现实世界的自行车共享系统中。
然而,上述基于用户的方法往往没有将空间信息(如自行车和用户的空间分布)和用户的信息(如步行所需时间)作为定价政策的影响因素。Pan L等人[36]将这一问题视为共享自行车服务经营者与环境之间的相互作用,并将其描述为MDP。在这个MDP中,每个地区的状态都由自行车的供应量、需求量、到达量和其他相关信息组成,动作可以表示为当前地区ri在总预 算B限制下的 一 种定价 策略这一策略通过价值为的奖励,激 励用户步行前往距当前地区ri距离为x的附近区域借还第k辆车。使用函数表示用户接受定价动作建议所需代价,当当前区域无车可用且时,会发生流单。这一任务的优化目标即最小化流单率。这一设置产生了一个连续的高维行动空间,且该空间维数随着指数增长。为了解决这一问题,Pan L等人[36]提出了一种名为分层强化定价(hierarchical reinforcement pricing,HRP)的深度强化学习算法。HRP算法建立在深度确定性策略梯度(deep deterministic policy gradient,DDPG)算法[41]的基础上,并使用了层次化的强化学习框架。这一算法的核心思想是将整个目标区域的Q值分解为多个较小区域的子Q值,其中,分别表示子区域rj在时间t的状态和动作,uj表示模型参数。该分解方法解决了高维输入中空间和时间依赖导致的复杂性问题,同时在分解过程中引入了一定误差。因此,HRP算法通过一个本地化模块fj(·)引入空间依赖性,从而纠正由于 子状态 和子动作之间的相互关联和分解而引入的Q函数估计偏差,因此可以表示为,以获得更小的输入空间,减小训练误差。该研究证明了HRP算法对收敛性的改进效果,并在摩拜单车数据集上证明了其性能优于现有算法。
4 资源分配问题
资源分配问题主要研究如何在多种资源与多个使用者之间建立合理、有效的分配,以优化整体的资源使用效率。根据问题中资源与使用者的匹配复杂程度,可以将资源分配问题划分为单段分配问题(如出租车派单、广告分配)和多段分配问题(如供应链管理)。经典的离线分配问题本身并不难以求解,通常可以采用匈牙利算法或网络流的方式获得最优的分配方案。但在实际应用中,由于分配中的一方或双方具有动态性,通常没有办法获取求解所需的所有信息。例如在出租车派单问题中,某个区域的空闲车辆是动态变化的,同时乘客的出现也是具有不确定性的。在这种动态性下,快速地建立高效的匹配来降低司机空载时间及乘客等待时间是非常具有挑战性的。下面分别针对单段分配和多段分配对相关文献进行梳理。
4.1 单段分配问题
在单段分配问题中,资源与使用者之间的匹配关系是一次性的。针对单段分配问题的强化学习研究主要集中在出租车派单、在线广告分配等问题中。下面从这两大类场景出发,介绍相关的典型研究。
(1)出租车派单问题
派单问题主要指如何满足实时出现的乘客需求,使得用户等待时间和司机空载时间尽可能短。一直以来,派单问题在交通优化问题上都有广泛的研究[5-6,42-43]。2009年,Alshamsi A等人[44]开始使用多智能体技术解决派单问题,没有使用强化学习的机制解决这个问题,而是使用事先制定好的规则指导各个智能体的行为,显而易见,这种情况下智能体的适应能力是受限的。
自从网约车兴起,由于场景本身的复杂性,越来越多的工作开始关注如何使用强化学习技术进一步改善派单效果。2018年滴滴出行科技有限公司联合密歇根州立大学的研究人员提出使用强化学习方法对出租车进行调度,平衡各个区域的供需关系[45]。在他们的模型中,整个城市被划分为由面积相等的六边形构成的若干网格,并将一天拆分成144个时间片。在每一个时间片内产生的订单,首先使用网格内的车辆进行匹配,若无法得到满足,再使用邻居网格中的可用车辆进行匹配。在具体建模中,每个车辆被建模成一个智能体,智能体能够观察到的状态为,其中,st表示t时刻的全局信息,gi表示该智能体对应的网格。智能体的动作空间iA包含7个动作,表示下一时刻能够到达的网格,其中,前6个动作表示移动到当前所在网格的6个邻居网格,最后一个表示留在当前网格。每个智能体i都有一个奖励函数Ri,具体来说,设智能体i在t时刻采取动作为该动作获得的奖励是在该智能体所处的网格中包括它自己在内的所有智能体在t+1时刻接收的订单收益的平均值。这样设计奖励函数的好处有两点:一是鼓励车辆自发地从供给多的网格流向供给少的网格;二是避免所有车辆都为了追求利益而集中到热点区域。在策略学习方面,参考文献[45]提出了两种带有上下文信息的学习算法:上下文深度Q网络(contextual DQN,cDQN)算法和上下文多智能体动作-评价算法(contextual multi-agent actorcritic algorithm,cA2C)。在cDQN算法中,作者利用全局信息共享以及每个网格内的奖励平均分配这两个特性,将对每一个智能体每个动作的Q值的计算转化为仅对当前状态下每一个网格的Q值的计算,即仅计算,其中,gd表 示 动作中指定的目的地。基于这一点,所有智能体可以共享一个全局的Q值。而上下文信息主要体现在两个方面:地理上下文信息和协作上下文信息。地理上下文信息主要根据地理位置,对有效的区域进行编码;协作上下文信息主要在可行的动作上进行限制,避免有车辆从A地到B地的同时还有车辆从B地到A地。除此之外的部分就是一个标准的DQN算法。cA2C算法中也有类似的处理,这里不再赘述。在结果方面,通过在滴滴出行提供的数据上进行模拟,可以发现基于cDQN和cA2C的方法在总收益和订单的接受率上都有显著提高。
上述方法主要存在两个问题。首先,作者只使用强化学习的技术平衡了各个网格中的供需关系,但是最终车辆到乘客的匹配是通过规则实现的,因此整体上是一个两段式的解决方案。其次,所有的智能体共享一个全局的Q函数,是一个中心化的解决方案,在扩展性和复杂性上都存在一些瓶颈。2019年,Li M等人[46]提出了一种新的端到端的解决方案。与之前的工作相比,该工作主要有以下几点不同。首先在状态方面,每个智能体i可以基于一个观测函数,从全局信息获取一个自己独有的状态oi。全局状态包括订单分布、司机分布、全局时间信息、交通信息以及天气信息等。这些信息都能帮助智能体更好地进行决策。然后在动作方面,智能体i需要从oi包含的未分配订单中选择并进行匹配。接着在奖励方面,作者综合考虑了每个智能体实际接单的收益和订单目的地的潜在收益,很明显,后者是由环境以及所有智能体的行为决定的。这样做的目的是鼓励智能体之间更好地合作。最后在策略学习方面,作者提出了一种合作派单(cooperative order dispatching,COD)算法。该算法主要的创新是引入了平均场强化学习(meaning field reinforcement learning,MFRL)[47],即在决策的时候每个智能体单独进行决策并获取动作,而在训练的过程中,根据平均动作更新评价网络,进而影响动作网络。具体来讲,针对每一个动作ai,COD算法会为其计算一个平均动作,即完成动作ai后,将所在区域中其他司机的数量除以可接收订单的数量。这个平均动作会作为额外的信息被引入评价网络的更新当中。
关于派单问题,还有很多优秀的工作,例如上海交通大学与滴滴团队提出的一种完全分散化的多智能体强化学习策略[48],以及香港科技大学联合滴滴团队提出的一种组合优化与强化学习相结合的两段式解决方案[49]。限于篇幅,本文不再展开介绍,感兴趣的读者可以阅读原始论文获取更多细节。
(2)在线广告分配问题
同派单问题相比,在线广告分配的问题场景更清晰。对于广告平台,每天有大量的客户访问平台。平台通过向这些用户展示广告,从广告主处获取收益。目前主流的广告展示策略有两种,第一种是传统的合约广告,即平台与广告主签订合约,在一定时间内向一定数量、符合条件的用户展示该广告主的广告。合约达成后,平台会获取收益,反之,平台需要承担违约的惩罚。这种广告方式在在线广告的早期非常流行,但是近些年来,其市场份额逐渐被新兴的实时竞价(real-time bidding,RTB)方式占据。实时竞价最早在搜索广告中出现,当用户查询一个关键词时,广告主针对这个查询发起竞拍并向平台报价,平台根据报价选择广告进行展示。后来这种方式扩展到展示广告中,竞拍的依据也从查询变成用户属性。虽然近些年实时竞价的市场在不断扩大,但是合约广告仍然占据大量的市场份额。
在在线广告领域,一个典型的使用强化学习进行分配的工作是阿里巴巴团队于2018年提出的一种融合合约广告与实时竞价的解决方案[50]。假设有n个用户展示需要分配给m个合约。对于每一个展示,都有一组实时出价价格,对此展示平台可以选择分配给某一个合约广告或分配给出价最高的竞价广告。最终的优化目标是最大化合约广告和实时竞价的整体收益以及整体合约广告的质量。作者提出了一种比较新颖的方式,即为每个合约模拟实时竞价行为,并为每一次竞价展示出一个价格。然后平台像普通的实时竞价系统那样按照第二价格的方式进行广告分配展示。作者在假设所有展示信息和实时出价已知的情况下,建立了最优分配的线性规划,并根据互补松弛定理证明,只要合约对应的出价满足式(5),最终的分配策略就是最优的①具体证明过程参见参考文献[50]。:?
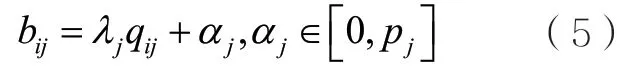
其中,bij、λj、qij、pj分别表示合约j对展示i的出价、合约j的质量权重、展示i相对于合约j的质量,以及违反合约j的惩罚。因此,问题的关键转化为求解合适的αj。但是在在线广告中,展示机会到来的情况和对应的出价难以预测,因此难以利用传统优化方法求解。为了解决这一问题,作者提出了一种多智能体强化学习的方法,即为每个合约分配一个智能体,让智能体动态地决定当前展示的出价。具体来说,智能体j在第t步决策的状态st包括时间信息(用于告诉智能体分配处于什么阶段)、合约当前的满足状态(多少比例已经满足,还有多少没有满足)以及在 1t−~t步之间智能体获取的收益rt−1。动作表示αj的调整因子,满足:

奖励的设计比较关键,作者首先定义原始即时奖励为t到t+1时刻平台整体的广告收益。在此基础上进一步定义:
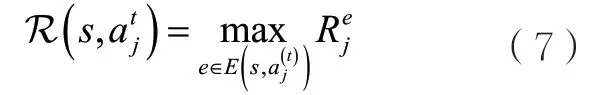
除了上述工作,还有更多的工作研究如何使用机器学习技术解决广告展示以及推荐系统中的问题,如参考文献[51-53],感兴趣的读者可以进一步研究这些工作。
4.2 多段分配问题
在单段分配问题中,只需要建立资源与使用者之间的关系即可,但是在多段分配问题中,面临的情况会更复杂。通常资源的流通会形成一个轨迹,需要优化流通中的每一步从而获得更好的分配效果,其典型的场景就是供应链问题。在供应链问题中,从原材料的生产、加工到销售通常需要多个步骤,而每一步的资源分配都会影响最终的收益,因而更考验分配算法的性能。下面对供应链的一些典型工作进行介绍。
供应链管理是一个传统的优化问题,但是其中供需关系的动态性使得传统的优化方法难以解决。随着强化学习的兴起,出现了大量使用强化学习解决供应链问题的工作,如参考文献[54-55],但是这些工作都使用了非常简单的供应链网络(网络只有两层,或者网络是一条链式的供应链)。Alves J C等人[56]在2020年改进了这些工作,他们将强化学习技术应用于一个更实际的场 景。在这个工作中,作者考虑了一个4层(供应商、工厂、批发商、零售商)的供应链网络,每一层都有两个参与者。供应商提供原材料,工厂加工成产品,然后再依次交给批发商、零售商进行售卖,其中原材料的供应是有一定容量的,链路中的每一个节点都有自己的库存容量,同时零售商还需要负责应对需求不确定性。整个供应链采取统一的控制方案,并且优化目标是在一个时间段内满足用户的商品需求,同时最小化运营成本。这里的运营成本包括4个方面:原材料的生产成本、工厂加工成本、各环节运输成本和仓储成本。
在MDP建模方面,i时刻的状态包括以下部分:(i+1)时刻各个零售商面临的需求数量、每一个节点当前的库存情况和(i+1)时刻的预计供给情况、当前时刻距离本次算法迭代终止剩余可执行动作的步数。智能体需要在每个时刻决定所有的原材料生 产数量和资源流通情况,具体包括两部分。第一部分是每个供应商需要生产的原材料数量。为了便于模型学习,所有动作都用比例表示,例如供给节点j生产原材料的动作aj表示生产cjaj个原料,其中,cj表示节点j的最大产量。第二部分是每个上游节点对下游节点供应的数量。如节点i对节点j的供应动作表 示有的库存需要从节点i运出,其中,,Si表示节点i的库存量。这样设计的目的是保证总输出量不超过库存量,同时剩余量将作为库存继续保留。在奖励设计部分,为了保证最终能够学习到全局最优的策略,作者将所有的成本都考虑到奖励设计中,即整个奖励包括生产、运输、加工、存储、原料废弃以及没有满足客户需求带来的惩罚等部分。考虑到问题的动作空间很大,作者采用一种基于PPO的专用于GPU并行加速的PPO2算法进行策略学习。通过训练并同主流的基于线性规划的算法进行对比,发现PPO2算法能够降低约87.4%的未满足需求,同时成本有约1.3%的下降。
5 装箱问题

装箱问题是一个NP完全问题,早在20世纪70年代中期,Johnson D S等人[57]就证实了对于现有主流的两种近似算法(降序首次适应(first-fit decreasing,FFD)算法和降序最佳适应(best-fit decreasing,BFD)算法)都能在时间复杂度的条件下达 到的近似性能保证。这两种方法都先将待装箱的物件按其大小进行降序排序。不同的是,对于一个给定的物件i,FFD算法将依次遍历箱子序列,并从中选择第一个能装下当前物件i(即剩余空间大于s(i))的箱子;BFD会从所有能装下当前物件i的箱子中选择剩余空间最小的箱子,即剩余空间大于s(i)且最接近s(i)的箱子。
在实际应用领域,产业界真实面对的不是上述最基础的装箱问题,而是装箱问题的多种变体,如二维装箱问题、三维装箱问题,或需要考虑不同装箱表面、箱子重量、箱子高度等信息的更复杂的装箱问题。根据实际情景中是否能提前知悉全部的物件信息,本文将装箱问题分为离线装箱问题和在线装箱问题,前者不仅可以知悉全部的物件信息,甚至可以根据策略决定装箱顺序;后者面对的是未知的物件序列,只能在物件到来时做出实时响应,执行装箱动作。
5.1 离线装箱问题
基础的离线装箱问题一般使用FFD和BFD这样的近似算法或简单的线性规划算法取得不错的结果。当面对的是更加复杂的实际装箱问题时,这些方法往往需要更加复杂的问题建模,耗费更长的计算时间。学术界和产业界都在装箱问题上进行过许多尝试,来自菜鸟物流的Hu H Y等人[58]将强化学习应用到装箱问题上。不同于使用固定大小的箱子的经典装箱问题,考虑到在真实物流问题上可以使用软材料来打包物件,而打包成本又与材料的表面积相关,这份工作针对的是经典装箱问题的一个变体:如何使用最少的包装材料把所有的三维物件打包好。具体来说,他们使用强化学习智能体来决定物件的打包顺序,而打包时物件具体的摆放位置和方向则由一套固定的常规的启发式规则来决定。强化学习智能体面对的状态空间由需要打包的所有物件的大小组成,表示为,其中,li、wi、hi分别表示物件的长、宽、高。他们从指针网络(pointer network)[59]中获得启发,将所有物件的大小信息依次输入一个长短期记忆(long short-term memory,LSTM)编码器中,再由一个LSTM解码器依次输出物件的打包顺序,即将物件的打包顺序作为智能体的动作空间。由LSTM编码器和LSTM解码器构成的神经网络指示的随机策略可以表示为p(o|s),而智能体的动作则用打包物件的表面积进行评估,表示为SA(o|s)。他们使用朴素的REINFORCE算法对策略进行更新。紧接着,Hu H Y等人[60]在上述工作[58]的基础上进一步利用多任务的形式,结合使用强化学习和监督学习,使智能体同时决定物件打包的顺序和摆放的方向。物件的打包顺序仍旧基于指针网络实现,不同的是在策略的更新算法上使用了PPO算法。而物件的摆放方向则由一个分类器决定,该分类器是使用目前所得最佳方案中的摆放方向作为标签训练得到的。该工作在实验部分使用了真实的数据集,实验结果表明,相比于之前广泛使用的启发式规则方法和Hu H Y等人[58]提出的强化学习方案,这样的智能体能取得更好的结果。同时,这一方法在真实生产环境中的应用也展示出,相比原生产线之前使用的贪心算法,该方法更能节省生产线成本。
不同于Hu H Y等人[58,60]采用类似于seq2seq(sequence-to-sequence)的建模方法,来自InstaDeep公司的Laterre A等人[61]把三维装箱问题建模成一个马尔可夫决策过程,并使用基于神经网络的蒙特卡洛树搜索算法来解决三维装箱问题。与前面的工作类似,强化学习智能体的状态空间由待打包物件的大小组成,即。不同的是,智能体的动作空间不只包含选择的物件编号,还包含其左下角的 摆 放位 置 坐标(xi,yi,zi)、物 件 摆放时的旋转方向oi,oi∈ {0 ,1,2,3,4,5}对应长方体的6种旋转结果,即完整的动作可以表 示为(i,xi,yi,zi,oi)。在该工作的解决方 案中,Laterre A等人[61]把三维装箱问题建模成一个单人游戏,为了进一步提升智能体的决策表现,他们还添加了一个奖励排名机制——动作的奖励值通过对最近的装箱操作的相对表现进行重塑得到。具体而言,智能体最近的性能表现会被存入一个缓冲区,对于设定的阈值α∈ ( 0,100%),仅当动作的性能表现超过缓冲区中α的记录时,智能体才能获得一个正向的奖励值。这样的奖励排名机制使得单个智能体在多次探索中得到类似双人游戏中与对手博弈的激励作用。实验采用的数据集由随机将原始箱子切成多个物件创建得来,相比于传统的蒙特卡洛树搜索算法、启发式算法和整数规划算法,该方法显示出更好的性能。
Li D D等人[62]认为使用启发式规则来决定物件的摆放方向和放置位置或通过切割原始箱子的方式来获取物件集合是这些方法的局限性,他们使用注意力机制来决定物件的摆放顺序、摆放方向和摆放位置。在Li D D等人[62]的建模中,状态空间由各个物件的信息组成,即其中表 示当前 物件 是 否已打包的0-1因子,表 示物件的长、宽、高,表示物件i当前的坐标,分别为相对于箱子前端、左端、下端的距离;动作空间的定义与Laterre A等人[61]的类似,由物件编号i、摆放方向oi和摆放位 置共同 构成;动作的奖 励 值 函数则是一个增量函数,奖励值由当前箱子里的物件的体积计算得到。智能体的训练使用了A2C算法,与Hu H Y等人[60]提出的方法和一个遗传算法进行对比,实验结果表明,这一方法具有更小的箱子间隙比率(bin gap ratio),其中,W、L、H分别表示箱子的宽度、长度和高度。
Cai Q P等人[63]提出了一种基于强化学习算法初始化的启发式算法优化框架RLHO(reinforcement learning heuristic optimization),并结合使用PPO算法和模拟退火算法来解决一维装箱问题。在这两种算法的结合中,PPO的输出方案被当作模拟退火算法的初始状态;而模拟退火算法则在有限次的迭代中寻找一个更好的解决方案,并基于最终找到的解决方案给PPO算法提供一个折扣未来奖励(discount future reward),从而指导PPO算法获取更优的初始状态。在智能体的设计方面,状态空间被定义为待装箱物件的一个全排列;动作空间则是这个全排列中任意两个物件的排序交换;并以受当前动作影响,待装箱物件的全排列对应的装箱成本的变化值作为智能体的即时奖励。这一工作的实验结果表明,基于RLHO框架,将PPO算法和模拟退火算法结合的方式能够取得比仅使用PPO算法或仅使用基于随机初始化的模拟退火算法更好的结果。
5.2 在线装箱问题
与离线装箱问题不同的是,在线装箱问题无法得知未来到达物件的信息,因而只能通过动态策略求解,不存在静态装箱解,相比之下,在线装箱问题要取得一个好的全局解更加困难。
与以往把箱子和待装箱物件的大小编码作为输入的方式不同,Kundu O等人[64]结合使用计算机视觉的技术,把箱子的实时状态和待装箱物件都表示为一个W×H的0-1矩阵(被物件占据的位置用0表示,可放置物件的位置用1表示)。这两个W×H的矩阵被拼接在一起,共同组成一个形状为W×2H的输入状态s。在强化学习智能体的动作空间的设计上,Kundu O等人[64]考虑的是待装箱物件的左上角的摆放位置,因而对于一个横截面为W×H的箱子而言,有W×H个可行的动作,再加上一个不将当前物件装入当前箱子的动作,共同够成了大小为W×H+1的动作空间。在奖励值函数的设计上,对于实际无法摆放物件的无效动作,给予一个负反馈;对于有效动作,则将物件摆放后的连通区域大小和摆放紧密度的乘积作为动作的奖励值。这里的连通区域大小指的是紧邻新物件4条边的区域数,可以对那些把新物件紧邻旧物件摆放的动作起到一定正向激励作用;而摆放紧密度则表示连通区域的大小占包含该连通区域的最小长方形的比值,用于鼓励使得连通的物件的形状更接近于长方形的摆放动作。实验结果表明,这种基于计算机视觉和强化学习的在线装箱方法能够取得比现有在线装箱方法更优的性能表现。
Verma R等人[65]在在线装箱问题的状态空间的建模上使用了和Kundu O等人[64]相似的思路——用一个二维矩阵表示箱子自上而下的投影。不同的是,由于研究问题从二维装箱转换到三维装箱,仅用0、1表示投影点的状态远不足够,因而每个投影点又进一步地使用一个值表示当前码垛物件的高度。此外,为了避免动作空间过大带来的探索效率过低的问题,也为了有效利用人为总结出来的有效规律(如把物件紧邻已有物件摆放会更高效),Verma R等人[65]使用一种两阶段决策的模式:首先基于一些基础规则筛选出物件摆放方向和位置的合法可行解,这些可行解主要包含将物件摆放在箱子的四角和紧邻已摆放物件的四角的摆放方式;其次,基于DQN算法的价值函数,从中选择一个摆放方案。在奖励值函数的设定方面,作者认为在三维装箱问题上没有显式的单步奖励,他们通过将装箱序列的最终奖励值定义为整个装箱序列最终的装箱比率,并结合一个指数衰减函数来反推得到每步的单步奖励值的方式,推进这一强化学习智能体的训练学习。
来自国防科学技术大学的Zhao H等人[66]使用了A2C的算法,其利用传感器获取箱子当前的状态信息,得到一个自上而下视角的码垛高度的投影矩阵H,假定大小为L×W。与此同时,待摆放物件i的长li、宽wi、高hi信息也被分别填充进3个L×W的矩阵中,构成形状为L×W×3的待摆放物件i的大小信息Di。而智能体的状态空间则由把H和Di拼接得到的L×W×4的信息输入一层状态卷积网络得到。同样,为了避免探索过程中的无效动作过多(这里的无效动作指的是无法摆放物件的动作),Zhao H等人[66]引入了一个可行动作空间掩码的预测器,而智能体仅在actor的输出中选取未被可行动作掩码预测器筛除的有效动作。掩码预测器的监督学习机制使得智能体的交互学习过程以更快的效率收敛。对于奖励值的设计部分,直接使用每一步动作带来的箱子空间占用率的提升量作为单步奖励,实验结果表明,这种单步奖励的设定方法要优于将最终箱子空间占用率作为最终奖励值的方法。
6 结束语
资源优化问题无处不在,更好的资源优化方案会带来更好的经济、社会效益。本文调研了强化学习在资源优化领域的最新应用,并针对3类重要的优化问题,即资源平衡问题、资源分配问题和装箱问题,就各个问题的特性、各个解决方案的问题建模和算法设计展开了详细介绍,以期能帮助读者更好地理解各领域。
虽然强化学习在解决实际资源优化问题方面取得了很多重要突破,但是目前仍存在一些问题亟待解决。首先,训练强化学习算法需要建立模拟环境或大量的历史数据,这提高了部署强化学习的方案门槛,很多小规模的优化场景很难应用。其次,训练算法需要大量计算资源,同时为了应对实际问题中的动态变化,需要定期地更新模型。这些都代表着巨大的计算成本。最后,大部分强化学习方案不具备普适性,需要根据具体的业务场景进行定制。这就需要大量强化学习专家的参与,难以形成规模效应。鉴于这些问题,研究者期待数据依赖更小、计算成本更低并且具有普适性的强化学习解决方案的出现。
