图的某些特殊性质的谱条件

王 磊，蔡改香，刘 莉

（安庆师范大学数理学院，安徽安庆246133）

设G=(V(G),E(G))是n阶简单图，其顶点集为V=V(G)，边集为E=E(G)。记Gc=(V,Ec)为图G=(V,E)的补图，其中Ec={xy:x,y∈V,x≠y,xy∉E}。顶点v的度d G(v)指G中与v关联的边数，G的最大度与最小度分别记为Δ(G)和δ(G)。图G的邻接矩阵A(G)=[aij]n×n，当vi、vj相邻时，aij=1，否则aij=0，i,j=1,2,3,…,n。A(G)的最大特征值μ(G)称为G的谱半径。设S⊆V，图G[S]表示以S为顶点集，以G中两端点均在S中的边为边集的图，若图G[S]中无边，则称S为G的独立集。G中含点数最多的独立集所含点数称为G的独立数，记为α(G)。如果G中所有顶点的度都相等，则称图G为正则图。如果Δ(G)=δ(G)=n-1，则称G为完全图，记作Kn。如果图的顶点集V可以被划分为互不相交的子集X和Y，使得V=X⋃Y，且任意边uv满足u∈X，v∈Y或u∈Y，v∈X，则称G为二部图，记作GBPT=(X,Y;E)。若对任意u∈X，d GBPT(u)相同，且任意v∈Y，d GBPT(v)也相同，则称GBPT为二部半正则图。设G1=(V1,E1)，G2=(V2,E2)是2个顶点不相交的简单图，它们的并图为G1⋃G2=(V1⋃V2,E1⋃E2)，联图为G1∨G2=((G1)c⋃(G2)c)c。对于非负整数k，若连续连接图G中的度和不小于k的不相邻点对，直到没有这样的点对存在，所得到的图称为图G的k-闭包，记作clk(G)。图G的k-闭包是唯一确定的，与所增加的边的次序无关，并且在clk(G)中任意不相邻点对u，v，有d clk(G)(u)+d clk(G)(v)≤k-1。其余相关概念和术语可参考文献[1]。

如果一条闭路径的起点和内部顶点互不相同，则称它为圈，一条包含图G中所有顶点的路称为哈密尔顿路，一个包含图G中所有顶点的圈称为哈密尔顿圈。若图G包含一个哈密尔顿圈，则称图G是哈密尔顿图。若图G中任意两个顶点都被一条哈密尔顿路连接，则称G是哈密尔顿-连通图。设X是图G的任意顶点集且X⊂V(G)，这里X中顶点数为s，如果图G-X是哈密尔顿-连通图，则称图G是s-哈密尔顿-连通图。设S表示图G中s个顶点的集合，如果对任意正整数i(3≤i≤s)，在图G中均存在圈C，使得|V(C)⋂S|=i，则称图G为S-泛圈图。冯立华等人在文献[2]中提出了给定大的最小度的图是s-哈密尔顿图或s-路-覆盖图的谱充分条件。余桂东等人在文献[3]中根据补图的谱半径提出了给定大的最小度的图是s-连通图、s-路-覆盖图、s-边-连通图的充分条件。受文献[3]的启发，本文主要根据补图的谱半径提出给定大的最小度的图是s-哈密尔顿-连通图、S-泛圈图或α(G)≤s的充分条件。

1 预备知识

下面介绍需要用到的4类特殊图类及引理。

NP1是满足下列条件的n阶图的集合：G1∨G2，其中，G1是n-k+r阶的(n-k-1)-正则图，G2是Kk-r的生成子图。

NP2是满足下列条件的n阶图的集合：Gc1∨G2，其中，G1=(X,Y)是阶为n-s-2+r的二部半正则图，并且对任意顶点u∈X，v∈Y分别有d G1(u)=k-s-1，d G1(v)=n-k-1，G2是Ks+2-r的生成子图。

NP3是满足下列条件的n阶图的集合：Gc1∨G2，其中，G1=(X,Y)是阶为n-s+2+r的二部半正则图，并且对任意顶点u∈X，v∈Y分别有d G1(u)=k-s+3，d G1(v)=n-k-1，G2是Ks-2-r的生成子图。

NP4是满足下列条件的n阶图的集合：G c1∨G2，其中，G1=(X,Y)是阶为2s+r的二部半正则图，并且对任意顶点u∈X，v∈Y分别有d G1(u)=k+2s-n+1，d G1(v)=n-k-1，G2是Kn-2s-r的生成子图。

引理1[4-5]（1）设n，s是正整数且s≤n-4，那么“图G是s-哈密尔顿-连通图”是(n+s+1)-稳定的。

（2）设n，s是正整数且3≤s≤n，那么“图G是S-泛圈图”是(n+s-3)-稳定的。

（3）设n，s是正整数且s≤n，那么“α(G)≤s”是(2n-2s-1)-稳定的。

引理2[4]设P是n阶图G的一个性质，如果P是k-稳定的且clk(G)有性质P，那么图G本身就有性质P。

引理3[6]设G是一个边集非空的图，则如果G是连通图，当且仅当G是正则图或二部半正则图时等号成立。

2 主要结果

定理1设G是n阶简单图且最小度δ(G)≥k≥1，k-s+2≥0，n≥2k+1。如果μ(Gc)≤则G是s-哈密尔顿-连通图，除非G∈NP1或G∈NP2。

证明假设图G不是s-哈密尔顿-连通图，构造闭包H:=cln+s+1(G)。根据引理1（1）及引理2，图H不是s-哈密尔顿-连通图，因此H中任意两个不相邻顶点u，v的度和至多为n+s，对任意边uv∈E(H c)，有

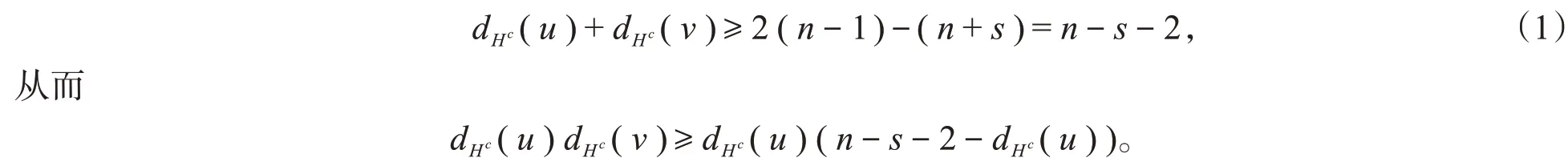
因为d H(u)≥d G(u)≥k且d H(v)≥d G(v)≥k，所以有d Hc(u)≤n-k-1，d Hc(v)≤n-k-1。结合式（1），可得dHc(u)≥n-s-2-dHc(v)≥k-s-1，dHc(v)≥n-s-2-dHc(u)≥k-s-1。

设f(x)=x(n-s-2-x)，其中k-s-1≤x≤n-k-1，这里f(x)是关于x的凹函数，于是f(x)≥f(k-s-1)=f(n-k-1)，自然有f(x)≥(k-s-1)(n-k-1)，当且仅当x=k-s-1或x=n-k-1时等式成立。因此，

3 结论

本文针对图的不同特殊性质，首先找到了相应的稳定性，然后进行了闭包运算，将复杂的原图是否具有某性质问题转化为闭包的补图来考虑，最后结合谱半径的性质及原图与闭包补图之间的微妙关系，巧妙地利用了补图的谱半径判定原图是否具有该性质。这种利用补图谱半径判定原图的某些性质是否存在的方法，为我们提供了一种新颖的思维方式。