一种基于网络模型的任务可靠性预计方法
2021-09-22陆志毅周云王璟玢
陆志毅 周云 王璟玢
(1.中国人民解放军海军装备部驻上海地区军事代表局 上海市 200241 2.中国航空无线电电子研究所 上海市 200241)
网络可靠性概念最先针对通信网络提出,其评估模型基于图论和设备物理失效,研究主要集中于改进算法和降低计算复杂度。20世纪90年代开始网络可靠性研究成为热点,提出了包括连通可靠性在内的很多网络可靠性概念,以及基于二元决策图(Binary Decision Diagram,BDD)等算法的方法论。21世纪后,对无线移动网络可靠性的研究成为热点,同时针对复杂网络的一些研究方法和成果也给复杂系统可靠性研究带来新的启发。
BDD作为一种描述布尔函数的数据结构,最早由AKERS提出,用来操作大数据函数[1]。之后,BRYANT给出了BDD的基本操作及算法[2],BDD得以广泛应用于硬件电路验证、组合优化、规划调度等研究领域中。
可靠性分析方面,COUDERT最早研究将BDD方法用于可靠性分析[3],并且BDD在网络连通可靠性分析领域的应用研究获得了大量的成果,实验证明利用BDD能够有效提升网络可靠性分析的性能。在一般的可靠性分析中,RAUZY等在内的大部分设计研究人员,主要将BDD用作故障树定量分析的工具[4],这虽然体现了BDD技术高效、精确的优势,但是就整个可靠性分析过程而言,仍较为繁琐。
任务可靠性是航电系统的重要指标,主要的分析方法有GO法,Petri网,以及包括可靠性框图、故障树和Markov分析等在内的典型可靠性建模分析方法。GO法依靠操作符和信号流建立GO图,然后按照信号流向和操作符运算规则进行计算。Petri网方法在系统功能性能设计基础上进行系统状态分析,进一步建立表征系统状态转变的Petri网模型,依靠对每次状态转换的定量分析,最终实现全过程的可靠性分析。以上方法建模分析过程较为复杂,部分存在状态爆炸的问题。
本文在BDD的网络连通可靠性分析方法,和传统的任务可靠性分析方法基础上,提出了一种基于网络模型的任务可靠性分析方法。将产品的可靠性特征抽象为网络模型,并利用基于BDD的网络连通可靠性分析方法,来对其进行分析,省略了前级的故障树分析过程,具有建模过程简单、分析高效准确、便于计算机自动化分析等优点。
1 BDD算法
1.1 基本概念
BDD是基于香农分解的有向无环图,是BDP(Binary Decision Program)的图形化表示,是对香农分解的简约化表达,可直观反映函数的逻辑结构。其数据结构空间高效合理,操作方法省时有效。
香农分解定理:令f是基于变量集X(X∈Bn)的布尔表达式,且x为变量集X中的任一变量,则:

其中在fx=1表示x=1时f的值。
香农分解是BDD分析和求解的基础。为简化表达香农分解,引入ite算子,香农分解定义为:
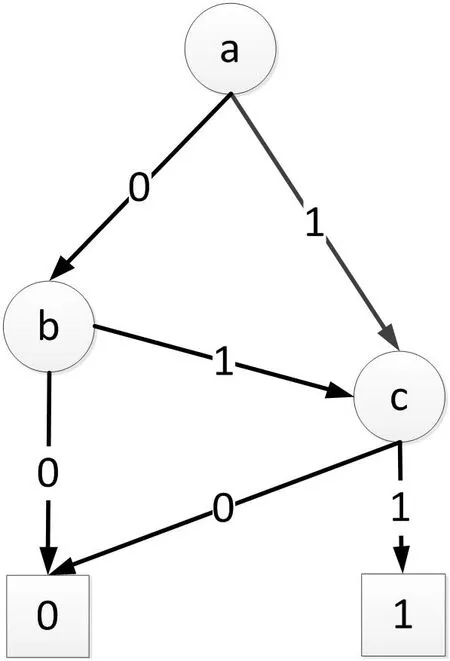
图1:BDD示例

其中F1=fx=1,F2=fx=0
BDD表示为G=
在BDD的基础上,对变量顺序施加约束后生成有序二元决策图(Ordered BDD,OBDD)。对OBDD进行约简,使其不包含同构子图,且节点的两条边指向不同节点,得到约简的OBDD(Reduced and Ordered BDD,ROBDD)。ROBDD对布尔函数的表达更为简洁有效,沿根节点向下索引时,每个节点在每条边上出现不多于1次,且为升序。
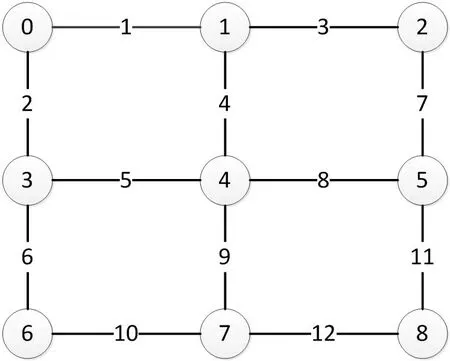
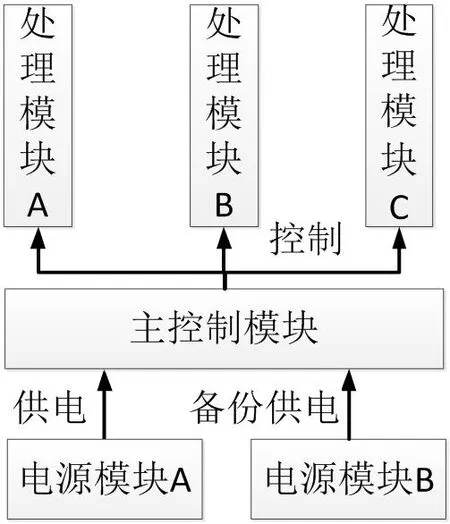
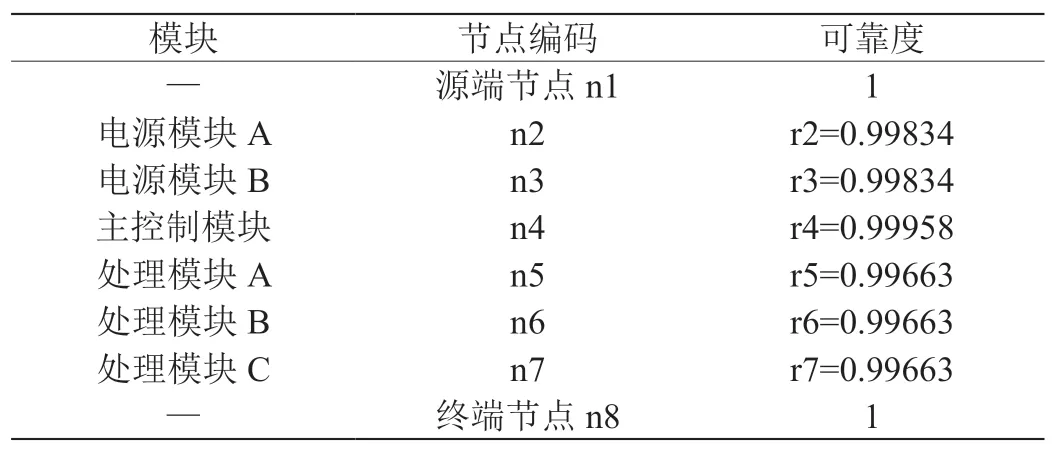
对ROBDD的构造而言,首先需要对变量顺序施加约束,为所有变量分别创建索引,并且保持变量索引顺序在整个构造过程中不发生改变。例如xi BDD规模和计算量依赖于变量排序,不合适的排序会使BDD规模变得很庞大。目前针对BDD排序有很多算法,如精确变量排序算法,动态变量排序算法,启发式变量排序算法,优先排序变量和道路排序分解策略等等。其中,广度优先排序策略(BFS)和优先级排序策略(POS)应用比较广泛。 1.2.1 广度优先排序策略(BFS) 广度优先边排序策略,是基于广度优先原则索引所有网络节点,并在索引过程中对未排序的边实施排序。 图2:BFS排序示例 图3:POS排序示例 图4:某综合处理设备功能原理图 对给定网络G=(V,E),广度优先排序的过程如下: (1)取∀u∈V作为广度优先排序的起点,标记u 状态为已检索,并将u 放入FIFO; (2)若FIFO中存在元素,取元素u,检索与u 关联的边ei=(u,vi)并进行排序,如果vi未标记为已访问则完成标记后放入FIFO; (3)重复步骤ii至FIFO为空,即完成排序。 以3×3晶格网络为例,对各边进行广度优先排序,图2为排序结果。 1.2.2 优先级排序策略(POS) 优先级排序策略的主要过程为:先按节点优先级规则完成节点排序,若关联多条边的两个节点都已排序,则以边优先级规则对这些边排序。优先级排序策略的节点优先级规则如下: (1)关联的节点中已排序节点数量多的优先; (2)关联的节点中已排序节点数量相同时,其关联已排序节点排序靠前的节点优先。 优先级排序策略的边优先级规则如下:与边关联的已排序节点排序靠前的边优先。以3×3晶格网络为例,对各边进行优先级排序,图2为排序结果。 表1:模型信息 1.3 基本运算 为了计算的方便,BDD的运算一般不直接进行香农分解,主要直接采用一些基本运算规则。 令布尔表达式P和H如下: ◇表示任意逻辑运算,则P和Q之间的逻辑运算用 BDD 运算表示如下,: 连通可靠性是最早开始的网络可靠性研究,与传统可靠性一致,以概率统计理论为基础,辅以图论作为网络“拓扑特殊”的支持,是目前网络可靠性中最被认可的部分。 本文探讨的任务可靠性网络模型,主要思想是将与系统任务完成相关的功能流和数据流关系,以有源网络形式进行表达,将任务可靠性分析问题转化为有源网络源端到终端的两端连通可靠性问题。任务可靠性网络模型可表达为: 其中N表示模型的节点集合,L表示模型的边集合,R表示节点可靠度集合。 设N中有m个节点,则任意节点ni(ni∈N,1 从节点np到节点nq的任意边lj=(np,nq),lj∈L,表示为保证任务的完成,节点np到节点nq间的功能或数据流。 任意元素ri∈R,表示节点ni的可靠度,规定几点S和T的可靠度值为1。 在本文的模型中有以下假设: (1)任一节点ni只存在正常(即ni=1)和故障(即ni=0)两种状态; (2)任两个节点间的故障是相互独立的; (3)任一边lj为正常状态; (4)布置表征任务开始的网络源节点S; (5)布置表征任务成功的网络端节点T; (6)对任务可靠性分析层次相应设备进行编号,将已编号设备布置为中间节点; (7)根据任务活动,添加网络的边,使源端节点S连接到终端节点T。 图5:任务可靠性网络模型 图6:任务可靠性网络模型BDD 基于网络模型预计任务可靠性,即为计算网络模型源端节点S到终端节点T的连通可靠性。基于ROBDD的网络模型任务可靠性分析,基本思想为:先由网络的最小路集求得网络的BDD,然后根据BDD求解连通可靠性的不交化积和表达式,最终完成任务可靠性预计。 假设有向网络的节点集为N={ni}(i=1,2,…,s),边集为L={li}(i= 1,2,…,t),若要求n1到nt的可靠度,算法过程如下: (1)从源节点开始,利用BFS或POS等排序策略对任务可靠性网络模型各边进行排序; (2)求出n1到nt的最小路集。设已求出为为网络模型最小路集的逻辑结构函数.其中,m表示最小路集数,fj表示某条最小路集j的所有节点布尔值的与; (3)按照排序结果,作f的BDD; (4)在逻辑结构函数f的BDD上搜索从根节点到叶结点为1的路径,则可获得F的不交化最小路集其中gi表示最小路集经变换后得到的不交和,p表示变换后得到的不交和项的项数。 任务可靠度可用下面的概率和公式直接进行计算: 考虑某综合处理设备,其功能原理如图4所示。 该综合处理设备主要完成数据处理任务,具有双余度电源设计,由主控制模块进行资源调度,由三个处理模块提供数据处理的硬件资源,主控制模块视当前资源占用情况,调用其中一个完成当前数据处理需求。 任务可靠性分析在模块层面进行,对各模块进行编码,并求得时刻t的可靠度,如表1所示。并建立任务可靠性网络模型,利用POS排序策略对模型中各边进行排序,如图5所示。 列出图5所示网络,其逻辑结构函数为: 进一步作出该表达式对应的BDD见图6。 由BDD列出ST连通可靠性的不交化和表达式,即综合处理设备的任务可靠性表达式: 计算得任务可靠度R=0.9995772,与使用可靠性框图模型求解的结果一致。 BDD方法被广泛用于网络连通可靠性求解,对复杂的逻辑关系计算呈现出较高的效率和准确度。本文在网络连通可靠性基础上,提出了一种根据产品功能流和数据流建立的网络模型,并将产品任务可靠性转化为网络连通可靠性进行求解的方法,给出了模型建立和基于BDD进行求解的方法。最后本文介绍了一个示例,说明该方法是可靠的。任务可靠性网络模型BDD如图6。 该方法尚需进行更多的模型转化、模型规范等方面的研究,但是提供了面对复杂系统的任务可靠性预计的一种新思路,有以下两方面可能的优势: (1)模型建立方式简单,便于利用各种语言和建模方式描述的功能性能模型直接转化而来,便于与基于模型的系统工程结合。 (2)计算方式高效,准确,利于计算机进行计算,方便形成计算机辅助分析的工具链。1.2 排序策略


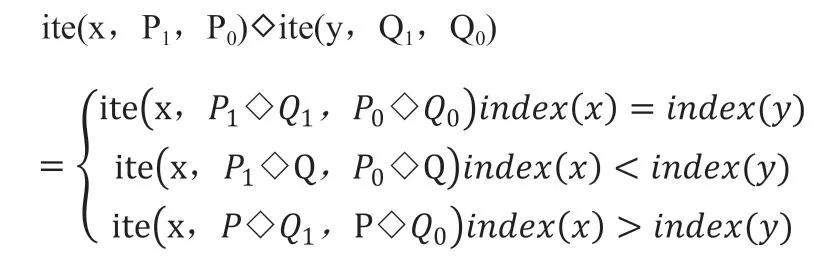
2 任务可靠性预计
2.1 网络结构模型

2.2 任务可靠性预计


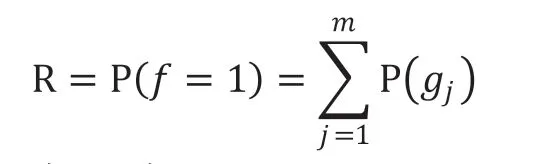
2.3 案例分析
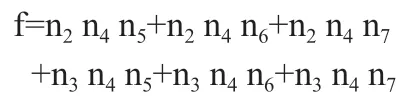
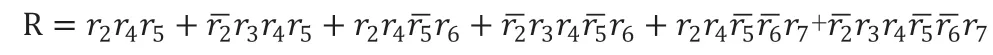
3 总结
