基于扭振信号的齿轮故障诊断方法研究
2021-09-21王伟
王 伟
(山西省煤炭职业中等专业学校,山西 太原 030032)
引言
齿轮系统是机械设备的主要零部件,其应用十分广泛[1],但齿轮故障会影响机械设备的精度和效率,甚至导致严重的机械事故。故齿轮故障的有效诊断具有重要的意义。
目前,齿轮故障的诊断大多是基于振动信号[2]。机械传动系统中的扭矩信号包含整个系统的传递特性,齿轮的啮合特性、负载的变化以及轴承支撑等都会引起轴的扭转振动,因此当齿轮发生故障时,扭振信号的幅值和相位也会发生变化。扭振信号包含更多的系统传动信息[3],正是由于包含更多的信息,使得故障特征的提取变得困难。
国内外针对机械传动系统的扭振问题已经开展了研究。X.Li 利用扭振信号检测汽轮发电机组的故障[4];Charles.P 基于扭转振动提出了柴油机故障的诊断方法[5];Kia 和Zhipeng Feng 等人通过扭转振动信号诊断行星齿轮箱故障[6];Xiang L 等人对机轴扭振信号的时频特性进行了研究[7]。
本文针对齿轮的磨损和断齿故障提出了利用MED 对扭振信号降噪处理,再通过VMD 实现对信号的分解,并对分解的分量进行频域分析,实现故障特征的提取。
1 齿轮啮合时扭矩波动特性
设主动轮和从动轮的基圆半径为rb1、rb2,齿数为Z1、Z2,其他参数如表1 所示。当输入扭矩为T1时,从动轮的输出扭矩T20为:
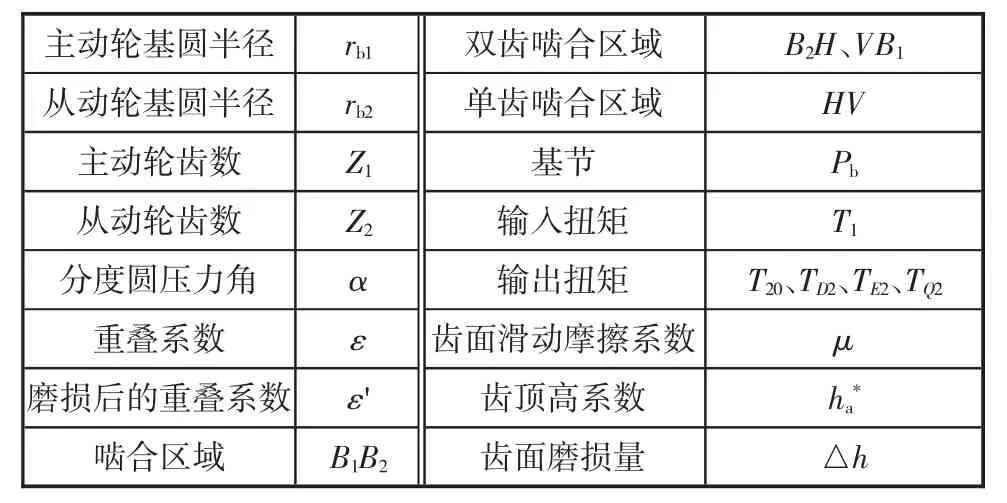
表1 本文所涉及到的参数

分析齿轮传动过程中的扭矩波动,如图1 所示。在渐开线齿轮啮合传动时,齿轮的实际啮合长度为B1B2。齿轮啮合时的重叠系数为ε,齿轮的基节为Pb,啮合线段B1B2=εPb,2(ε-1)Pb长度属于双齿啮合区,(ε-1)Pb长度属于单齿啮合区。
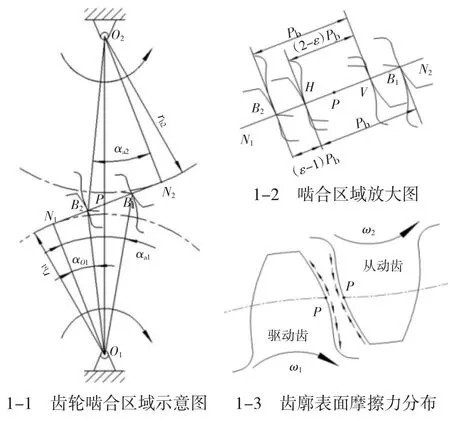
图1 齿轮啮合波动与受力示意图
2 两对齿啮合时扭矩波动特性
当齿轮双齿啮合时,假设法向载荷被完全均匀分配到两对齿上。如下页图2 所示,当从动轮一个齿在B2点啮合而另一个齿在V 点啮合时,它们承受同方向相等的法向载荷Fn2/2 以及反向相等的切向载荷Fn2/2。双齿啮合时齿轮的输入扭矩和所受载荷的关系如式(2)所示:
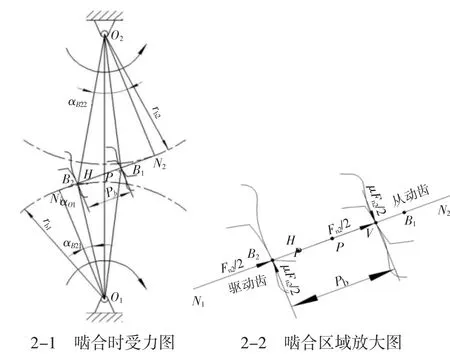
图2 双齿啮合传动图

2.2 单齿啮合时扭矩波动特性
2.2.1 在HP 区域
如图3 所示,当从动轮齿廓在HP 区域任意点E啮合时,所承受的法向载荷为FnE2,切向载荷为μFnE2。单齿在HP 区域啮合时齿轮的输入扭矩和输出扭矩与所受载荷的关系如式(7)(8)所示:
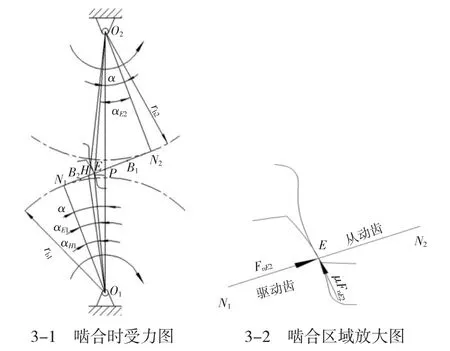
图3 单齿HP 段啮合传动图
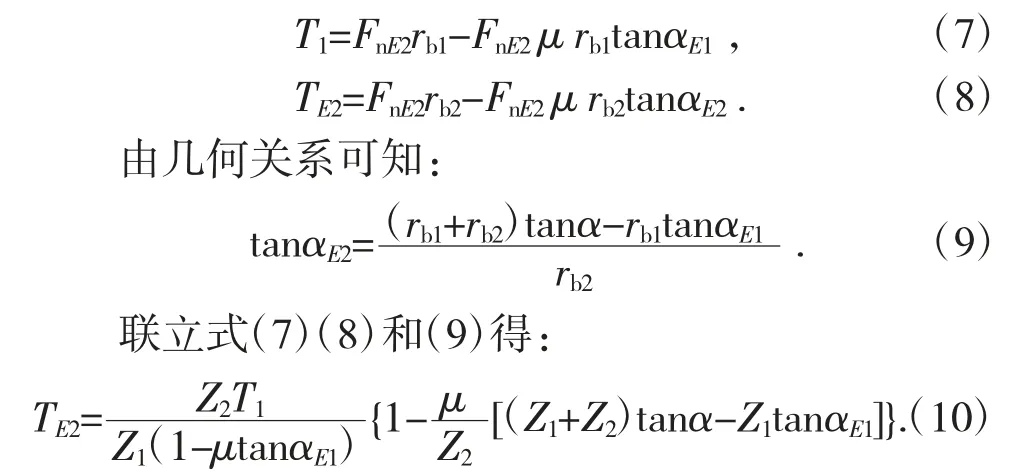
2.2.2 在PV 区域
如图4 所示,当从动轮齿廓在PV 区域中任意点Q 啮合时,所承受的法向载荷为FnQ2,切向载荷为μFnE2。单齿在PV 区域啮合时输入扭矩和输出扭矩与所受载荷的关系如式(11)(12)所示。

图4 单齿PV 段啮合传动图
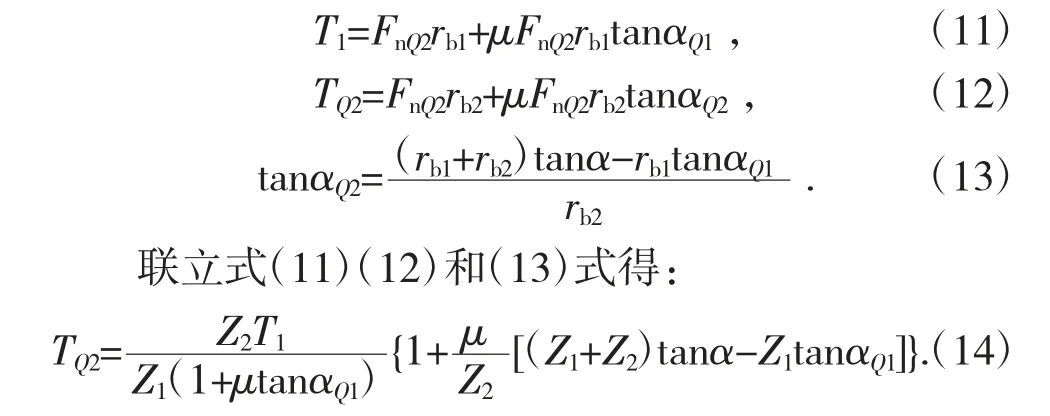
2.3 齿轮磨损后啮合区域的扭矩波动特性
齿轮磨损后,双齿啮合区域变小,单齿啮合区域变大,重叠系数变小。当齿轮表面磨损量为△h 时,齿面的重叠系数ε'为:

将重叠系数带入式(16)计算磨损情况下的压力角,再将磨损后的压力角带入式(6)(10)(14)中可计算得到输出扭矩。
当齿轮发生断齿时,原双齿啮合会变为单齿啮合,单齿啮合区会产生一段非啮合区域,重新啮合时会对齿轮系统产生冲击。
图5 为不同故障下齿轮的扭矩信号图。
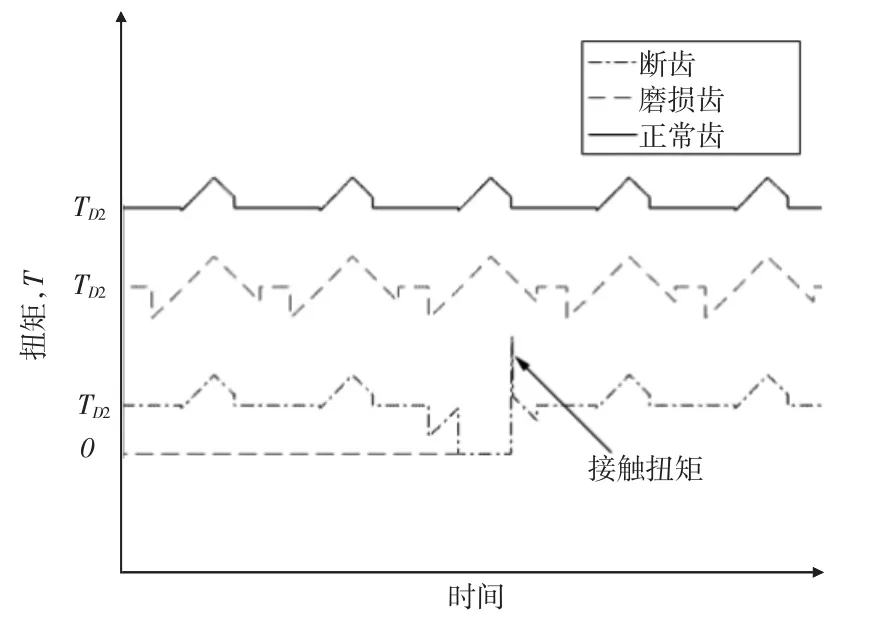
图5 各种状况时齿轮扭矩波动图
3 扭振信号数据处理方法
3.1 最小熵反褶积实验设置
最小熵反褶积(MED)是一种自适应系统的降噪方法,最早被Wiggins 用来提取地震反射数据[8]。目前该方法被应用于故障信号处理中,在轴承故障[9]和齿轮箱故障诊断[10]中有很好的应用效果。MED[11]方法可以用来很好地提取冲击脉冲,对冲击性故障信号的降噪效果较好。
逆滤波是一个求卷积的过程,公式如下:
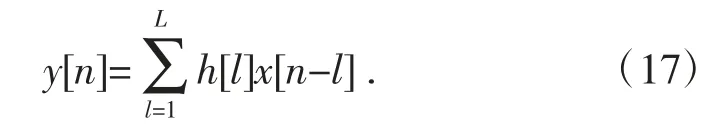
式中:L 是滤波器的长度,h[l]是滤波的卷积公式,x是输入信号,y 是输出信号。输出信号范数为:

图6 为扭矩信号处理前后对比图。
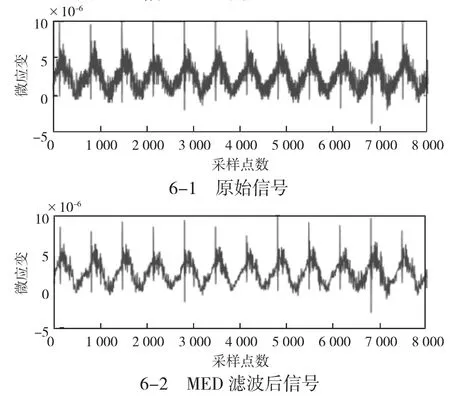
图6 扭矩信号MED 滤波处理前后对比图
3.2 变分模态分解
变分模态分解(VMD)是由K.Dragomiretskiy 等提出的一种多分量信号自适应分解方法[12]。目前该方法已经被用于机械故障的诊断[13]等领域。与EMD和LMD 相比,VMD 方法分解精度高、分解层数少且不存在模态混叠现象。
设VMD 分解得到的分量为uk,则
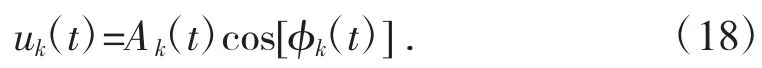
式中:Ak(t)为uk(t)的幅值;φk(t)为uk(t)的瞬时频率。
VMD 具体迭代运算过程如下:
1)初始化角频率、λ1和n;
2)n=n+1,开始计算;
5)根据λn+1(ω)=λn(ω)+τ[f(ω)-]计算模态分量λn+1(ω);
4 实验设置
试验台如图7 所示,用以模拟齿轮的磨损和断齿故障,用电机转速控制齿轮转速。

图7 试验台
模拟齿轮系统的参数如下:齿轮模数为2,压力角为20°,齿宽25 mm,材料45 钢。实验齿轮如图8所示。
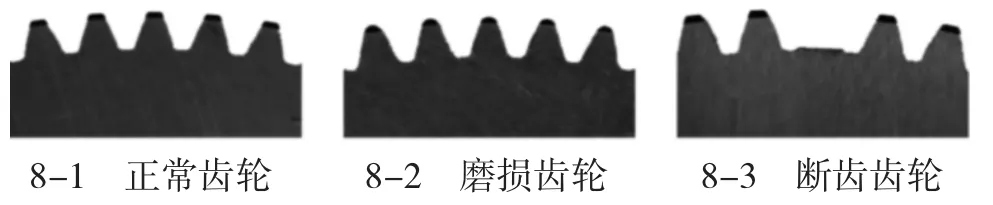
图8 实验所用的齿轮
实验选用无线扭矩采集传感器,将实验数据实时传送到采集系统中。实验台的整体示意图如图9所示。
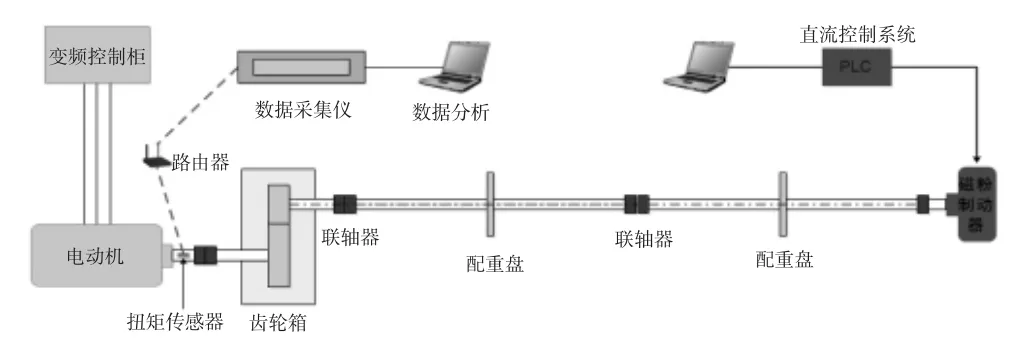
图9 试验台总体示意图
5 实验结果分析
分别模拟空载和2 N·m 两种负载状况,实验参数如表2 所示。
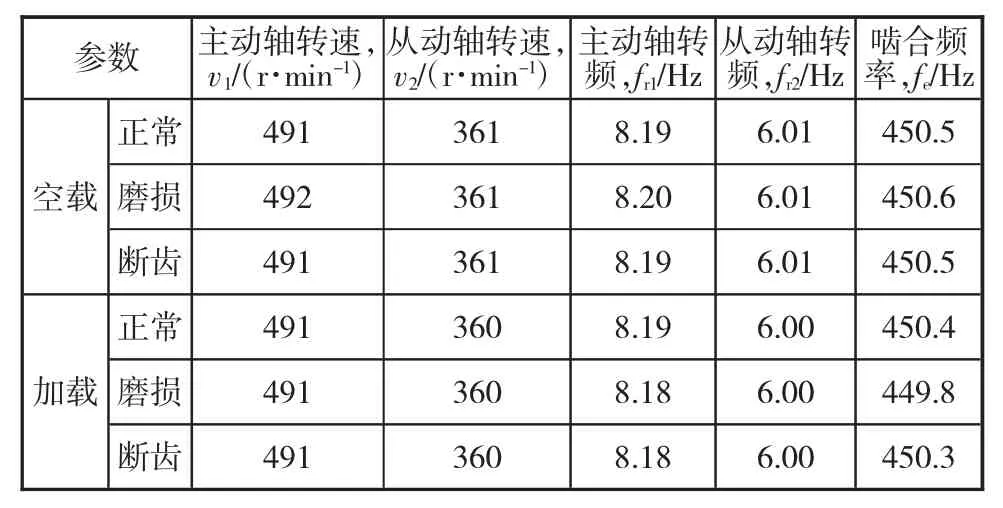
表2 各组实验的转频参数
本实验中利用EDM 和VMD 分解扭振信号,选取包含转频和啮合频率的IMF1 和IMF3 分量做出其频谱图(图10—图15)。
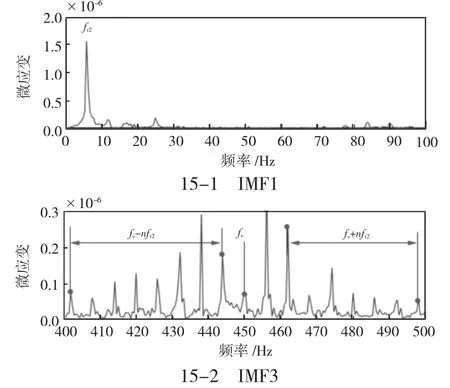
图15 加载齿轮断齿IMF1 和IMF3 频谱图
5.1 空载
从图10 可以看出,正常齿轮在低频段会出现主、从动轴转频及其倍频,在高频段出现啮合频率和边频。这些频率可能是由于轴自身的加工装配误差导致的。
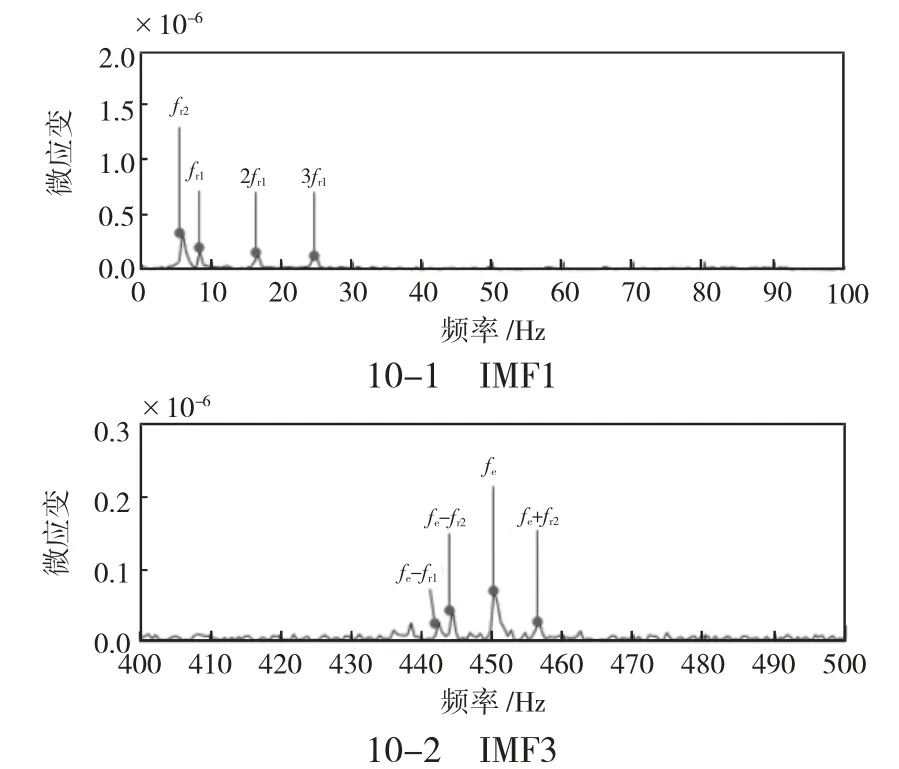
图10 空载正常齿轮IMF1 和IMF3 频谱图
从图11 和图12 可以看出齿轮磨损时,在低频段没有太大变化,但在高频段啮合频率的幅值明显增大。这是因为啮合过程的扭矩波动增大导致的。当齿轮断齿时,从动轴在低频段转频的幅值增大比较明显,这是因为啮合时在断齿区域产生了冲击力矩。

图11 空载磨损齿轮IMF1 和IMF3 频谱图
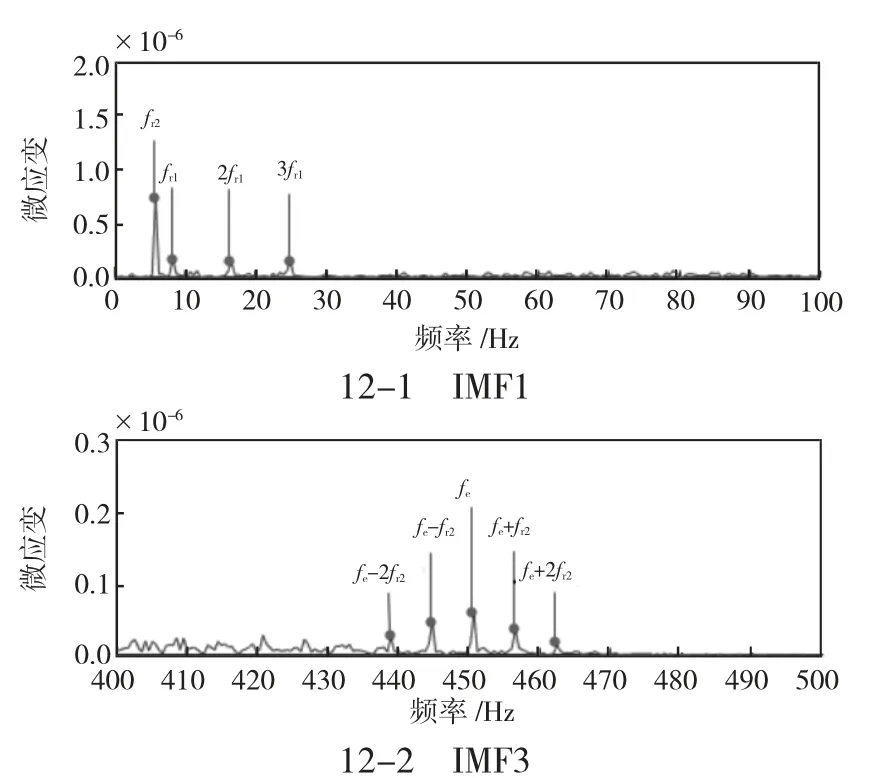
图12 空载齿轮断齿IMF1 和IMF3 频谱图
5.2 加载
在施加负载时,从图13 可以看出,正常齿轮在低频段会出现比较突出的从动轴转频,在高频段出现啮合频率和边频。相对于空载时,从动轴转频有大幅的增长,啮合频率的边频也有一定的增大,这是因为负载增加了振动幅值。
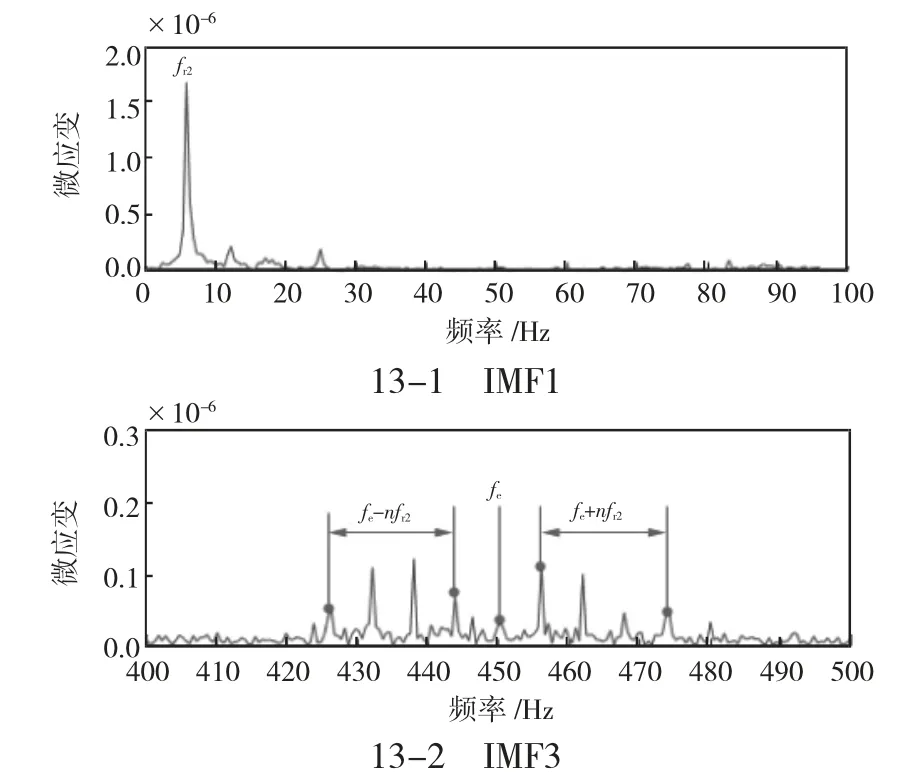
图13 加载正常齿轮IMF1 和IMF3 频谱图
从图14 和图15 可知,齿轮发生磨损时,在低频段没有太大的变化,但是在高频段啮合频率的幅值增大。而当齿轮发生断齿故障时,在低频段从动轴转频的幅值没有明显的变化,但高频段啮合频率的边频变多且幅值增大。这是因为断齿区域在发生啮合时产生的冲击力矩与负载自身的波动相比比较小,同时这个冲击力矩激发了更多的边频。
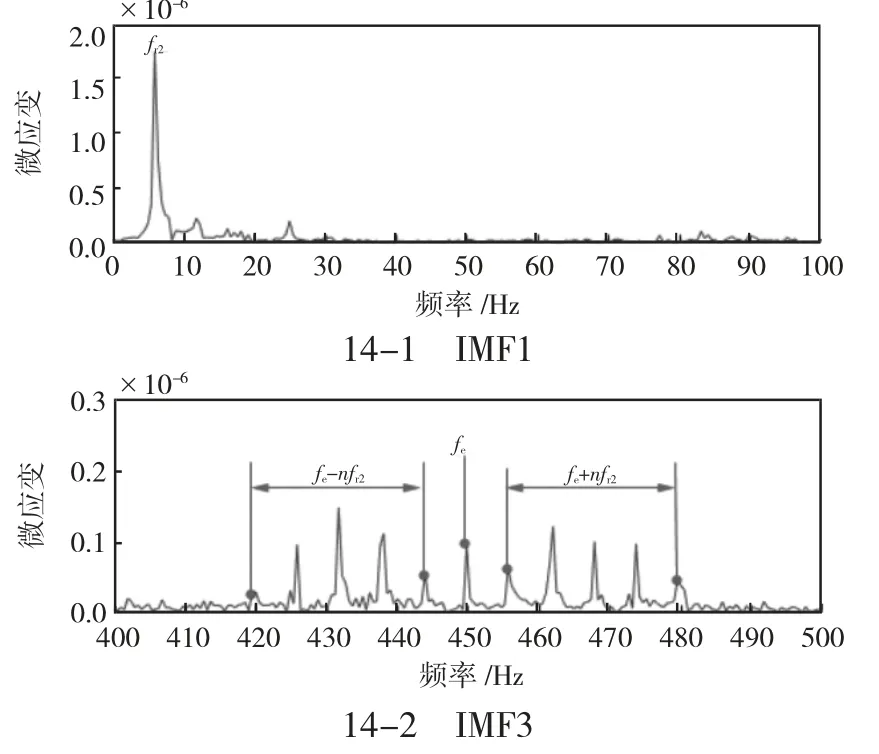
图14 加载齿轮磨损IMF1 和IMF3 频谱图
6 结论
1)扭振信号包含齿轮系统的传动特征信息,且受传递过程的影响较小,因此利用扭矩信号诊断齿轮故障是可行的。
2)本文所提的方法可以对齿轮故障做出有效的诊断。空载时通过从动轮的转频和啮合频率就可以有效识别出齿轮的磨损和断齿故障,而加载时应当注重啮合频率及其边频的变化。
