简支转连续T 梁桥截面优化分析

陶永靖，孙艺恒

（苏交科集团股份有限公司，江苏 南京 211110）

0 引言

在近年来的桥梁建设发展中，预应力简支转连续T 梁桥凭借施工工艺较简单、伸缩缝较少、施工工期较快等优点，逐步在桥型的选择上占据了重要的地位。因此，在满足安全使用的前提下，对其截面进行优化分析，以减小其截面尺寸，对改善T 梁桥的总体经济效益具有极其重要的现实意义。

由于简支转连续梁桥的主要施工造价体现在预应力钢束的数量、普通钢筋的数量、混凝土的体积，以及在施工过程中的人工费和机械台班费上，故若能在满足桥梁整体性能和使用要求的前提下对梁体的尺寸进行优化，就会减少梁体的混凝土用量，并对钢筋、模板等用量带来间接性的下降，则全桥相应的人料机费用均下降，必然能为结构带来一定的经济效益。传统的结构优化设计一般是一些有经验的设计人员先定量后定性，即参照设计要求结合自己的经验先确定结构的某些变量，经过计算分析得出此方案的优劣。如果效果不佳，则改变某一个或多个变量再进行设计验算。如此反复，直至找到一种合适的方案。暂且不说此种方法的烦琐程度，此种方法得出的结果虽然能够满足结构的各种要求，但不一定是最优方案，就会造成一些浪费或者不合理。而ANSYS 的优化模块对结构优化的分析只需要提供参数变量、状态变量和目标函数即可进行，并可以快速产生目标函数的最优值，得到最优方案[1]。

1 有限元模型的建立

根据40 mT 梁的标准截面尺寸，利用ANSYS 软件建立模型。在建模时，选取SOLIDE65 实体单元替代主梁混凝土，选取LINK8 单元替代预应力钢束。采用实际的截面尺寸位置建立节点，通过节点建立梁体混凝土和预应力筋。接着定义材料的属性并定义梁体的边界条件，然后进行映射体网格的划分。最后采用降温法施加预应力，同时通过节点耦合将混凝土和预应力筋结合起来，建立了如图1 所示的一联三跨中梁ANSYS 模型[2]。

图1 ANS YS 模型

通过MIDAS 模型提取其三跨中梁的弯矩包络图，得到其承载能力极限状态下桥梁的最大弯矩出现在第3 跨跨中的位置，如图2 所示[3]。以第3 跨跨中弯矩为控制弯矩，通过等效荷载转换的原则，采用试算法得到加载在第3 跨跨中的集中荷载为700 kN，换算荷载效率达到98.2%，符合换算要求。

图2 承载能力极限状态下的弯矩包络图

2 优化分析

2.1 优化参数的选择

2.1.1 设计变量

参照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(以下简称《公预规》)9.3.2 条规定：T 型或者箱型截面梁在预制时其悬臂厚度应该大于100 mm；若T 型梁用整体横向现浇的方式连接成整体或者箱型梁铺设横向预应力钢束时，两者悬臂端厚度应该大于140 mm。对于T 型和I 型截面梁来说，腹板处的翼缘厚度应大于1/10 梁高，并且若此处有承托存在，承托的加厚厚度可以考虑翼缘厚度；若承托底坡的tan α 大于1/3 ，取1/3。对于T 型、I 型和箱型截面梁来说，其腹板的宽度应该大于160 mm。若腹板内需要布设竖向预应力钢筋，则其上下两承托间的腹板高度一般取腹板宽度的20 倍以内[4]。本文对T 型梁截面尺寸的优化选取的参数如图3 所示的马蹄宽度、腹板厚度和顶板厚度。

图3 截面构造参数

本文依照《公预规》的各项尺寸参数规定，经过对交通部颁08 标准图的比较核定，对T1、T2、T3 的取值采取如下要求：结构尺寸的下限值为能够满足梁体内普通钢筋和预应力钢束横向布置，同时加上梁体混凝土的最小保护层厚度的最小值，上限值就取用08 部颁标准图中的尺寸，同时结合已建桥梁数据取用表1 所示尺寸范围。

表1 结构尺寸范围

2.1.2 状态变量

本文需要将优化后的梁体进行验算，以保证优化后的截面是满足结构设计要求的。结合设计变量的选择，选取三跨跨中截面的最大挠度、使用阶段跨中截面正弯矩区和梁端负弯矩区的正应力进行控制。根据规范规定，排除由于结构本身的自重而产生的挠度值，对于连续桥来说，主梁梁体产生的最大下挠值原则上要小于计算跨径的L/600[5]。对于部分预应力混凝土A 类构件来说，规范规定C50 混凝土的抗拉强度设计值为1.83 MPa，抗压强度设计值为22.4 MPa。

2.1.3 目标函数

此次对T 型梁桥的截面优化分析主要是达到经济效益的最优，排除施工工期等其他间接因素的影响，便是要优化得到T 型梁桥的体积使得造价降低，因此目标函数选为T 型梁桥的体积[6]。

2.2 加载模型的优化步骤

对建立完成的模型进行计算，在后处理模式中输出最后一个荷载步骤的结果，提取各跨中截面底缘和墩顶截面顶缘的挠度和应力值。同时通过事先定义各单元的体积得到梁体的总体积大小，并将此步骤定义成一个宏文件。接着使用ANSYS 的优化分析模块，载入已经定义的宏文件，然后对设计变量的范围加以指定，定义状态变量，并选择相应的优化方法，设置最大的循环次数。此时便完成了所有优化设计的前期准备内容。

2.3 优化结果的分析

此ANSYS 模型采用零阶优化方法进行优化设计后，根据设计变量的不同得到了8 个优化系列，提取各优化序列的变量和优化结果见表2。

由于优化的主要目的是对目标函数的分析，因此在ANSYS 中将这8 个优化系列以图标的形式显示体积变量，如图4 所示。

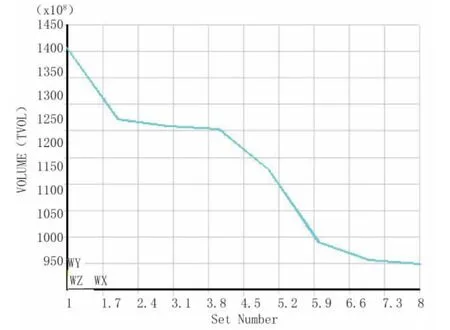
图4 体积变化值（单位：mm3）

由图5 可知，随着优化进程的深入，梁体总体积随着设计变量的变化逐渐减小，最小的体积出现在SET8，此时的优化体积为9.98E+10 mm3。结合表2得出此优化序列中马蹄宽度T1 减小为212.1 mm，腹板厚度T2 为160.4 mm，顶板厚度T3 为200.7 mm。由于在工程设计中一般采用较整的数据以便于施工，故此次T1、T2 和T3 取用220 mm、170 mm 和210 mm。

表2 优化序列的结果

通过在ANSYS 后处理模块中提取各跨跨中截面的挠度值，分析挠度值在各优化序列下的变化，绘制如图5 所示。

图5 各优化序列下跨中挠度值变化

由图5 可以得出，三跨T 梁跨中截面的挠度基本随着优化序列的递进而逐步增大。这是因为梁体在预加力阶段出现了反拱值，在集中荷载的影响下产生下挠值；由于截面优化后的尺寸变小使得截面惯性矩变小，从而产生挠度值一直增大的现象。前两跨的挠度值变化范围均在4 mm 以内，而第三跨的下挠值增幅明显大于前两跨，达到近11 mm。这是由于集中荷载的700 kN 在各优化序列中均加载在第三跨跨中，其截面尺寸相应地减小，挠度值的变化幅度必然大于前两跨。此时跨中最大挠度值出现在第8 序列第三跨跨中，为31.7 mm。而规范规定主梁最大挠度处原则上不大于计算跨径的L/600，即40000/600=66.67 mm，所以在此优化过程中对于挠度值的控制均满足设计要求[7]。

在ANSYS 后处理模块中提取各跨跨中截面底缘和墩顶截面顶缘的应力值，分析应力值在各优化序列下的变化如表3 和图6 所示。

表3 控制断面应力值随优化序列变化

图6 应力变化值

经过表3 和图6 的分析可以得出，各控制断面的应力基本随着优化序列的递进逐步变大，一号墩和二号墩的上缘应力值大于跨中截面底缘的应力，与实际结构的受力相吻合。由于在ANSYS 分析中，应力的负值表示为压应力，根据梁截面弹性变形的原理，此时8 个优化序列中梁体的受力特性均为全截面受压状态，最大压应力产生在第8 序列下一号墩墩顶为21.63 MPa。而规范对于抗压强度的规定为22.4 MPa，所以优化后的截面压应力均满足要求。

同时根据《公预规》5.7 规定，当混凝土构件布置了间接钢筋时，对于锚下局部受压区的尺寸需要符合γ0F1d≤1.3ηsβ fcdAln，其局部抗压承载力满足γ0F1d≤0.9 （ηsβ fcd+kρvβcorfsd）Aln，本文将不一一赘述。对预应力作用下锚下的应力计算得出T 型梁的截面尺寸中的T1 值必须大于270 mm 才能满足规范的要求，因此优化设计完成后的设计参数T1 值由优化后的212.1 mm 转变为270 mm。根据实际工程实践和已建桥梁，给出截面优化完成后施工图设计时T型梁截面尺寸的建议值见表4，中梁跨中与梁端截面尺寸如图7 所示。

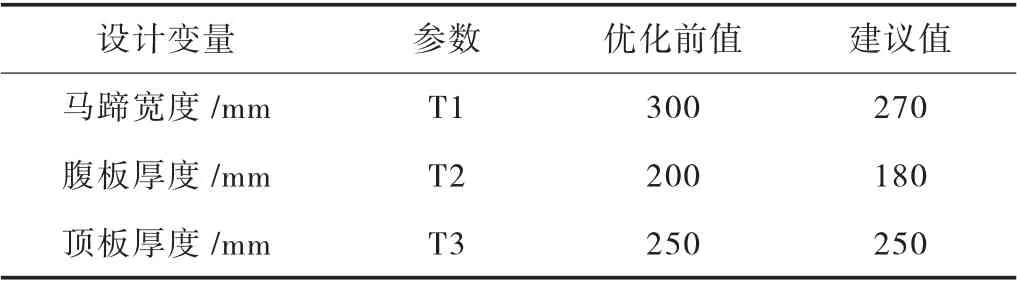
表4 设计变量建议值

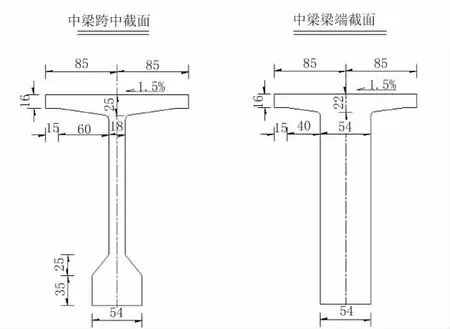
图7 优化后截面尺寸建议值（单位：cm）

3 结语

采用ANSYS 软件建立三跨一联的优化前中梁参数化模型，结合MIDAS 模型以第三跨跨中弯矩为控制条件进行荷载的等效替换，得到需要在第三跨跨中施加700 kN 的集中荷载。根据《公预规》的规定，选取模型的设计变量为马蹄宽度、腹板厚度和顶板厚度，并定义其变化范围，以各跨跨中截面的最大挠度和使用阶段跨中截面正弯矩和梁端负弯矩区的正应力作为状态变量，目标函数为T 型梁桥的体积。经过ANSYS 的优化分析， 得到了最小的体积9.98E+10 mm3出现在序列8。通过对各跨跨中和墩顶的挠度、应力验算，得到各优化序列下的截面尺寸均满足设计要求。但对局部承压截面尺寸和承载力的计算得到截面尺寸中的T1 值必须大于270 mm，在选择锚垫板时需要选择更高级别的锚垫板。因此，根据实际工程实践和已建桥梁，优化设计完成后的40 m T 梁设计参数马蹄宽度T1 变为270 mm，腹板厚度为180 mm，顶板厚度为250 mm。