浅析独柱曲线梁桥稳定性及抗倾覆对策

王紫玉

（北京市市政工程设计研究总院有限公司，北京市 100082）

0 引言

伴随国民经济的发展和综合国力的提升，我国城市建设进入一个新的纪元。为更好适应行车要求、节约建设用地，在市政和公路立交中建设了众多大曲率定向、转向匝道，曲线梁桥结构得到了广泛的应用。设计人员一般更注重构件强度的设计，而忽视支承体系的合理性。因此，本文通过对独柱曲线梁桥受力特点和病害形态的分析，结合具体算例，总结出影响独柱曲线梁桥稳定的因素，并提出相应的解决对策，从而为今后此类桥梁的设计提供一些参考和借鉴。

1 影响曲线梁桥稳定的潜在因素

近年来，桥梁失稳倾覆的现象频发，逐步引发社会的关注。曲线梁桥作为受力较复杂的一类桥梁，其稳定性问题显得更突出。在了解桥梁结构受力特点的前提下，把握结构强度和刚度的同时，还应构建一个良好的运营环境，保证结构整体可以在一个稳定的状态下正常工作。

1.1 结构受力特点存在安全隐患

（1）对于曲线梁桥，其变形表现为弯曲和扭转的叠加。在均布荷载作用下，弯桥在挠度和内力分配上，均是外边缘大于内边缘。这一特征随着曲率半径的减少而更加明显，因此对于小半径曲线桥梁，在结构设计伊始，内外腹板的受力状态便存在较大差异。

（2）曲线梁桥的支承反力也呈现出外梁变大、内梁变小的倾向。尤其是曲率半径小、静荷载比较小时，内侧支座更易“脱空”或出现负反力。此特点在连续曲线梁中越发突出。

（3）曲线梁桥的预应力效应对反力分配影响较大，在计算时不可忽视。

1.2 设计时并未引起足够的重视

部分设计人员更加看重上部结构的自身强度，至多为超载情况预留一定的安全储备，而忽视了结构的稳定性，缺乏对其空间性能的深入了解，在设计阶段就埋下了安全隐患。

1.3 超载的外因突显结构隐患

虽然交通运输业在不断发展，运输的形式也变得多元化，但是车辆陆运仍旧以其“点对点”的特性，占有极高比重和地位。而在经济利益的驱使下，超载现象频发，并成为设计人员的“噩梦”。经分析，大部分的现状桥梁倾覆事件，罪魁祸首基本上是超载车辆，对其进行合理限制，已经成为避免倾覆事故的重中之重。

2 曲线梁桥的失稳病害并究其成因

近些年，曲线梁桥事故频发。究其原因，还是稳定性问题。各种病害发生后，并未真正得到重视，久而久之，导致了结构的失稳破坏。

2.1 “爬移”现象

“爬移” 现象指曲线梁桥在运营过程中会出现纵向及侧向变位，并在长期反复的作用下不断地积累，造成梁体的“爬移”，从而导致支承体系的改变，以及伸缩缝等附属结构的破坏，如图1、图2 所示。造成其位移发生的主要外部因素包括温度荷载、预应力荷载、收缩徐变和汽车荷载（离心力和制动力）等[1]。

图1 纵向“爬移”

图2 侧向“爬移”

2.2 支座“脱空”

其主要表现为在车辆荷载和温度荷载的作用下，内侧支座“脱空”，造成原有的支承体系失效，新形成的支承体系在外荷载的作用下超负荷工作。造成内侧支座“脱空”的主要原因有支承体系的抗扭刚度不足、结构扭矩分布不合理，以及未设置拉力支座等。

2.3 支座“拉裂”

部分建成已久的桥梁，其中墩独柱支承采用橡胶支座，在温度荷载的作用下，梁体结构发生径向变位，橡胶支座在剪切作用下发生环向开裂而失效。

2.4 拉力支座破坏

计算手段的局限性和工况模拟的不周全，导致在桥梁设计时，虽然考虑到了曲线内侧支座的 “脱空”效应而设置了拉力支座，但其拉力设计值与实际值相差较大、选用支座的不合理，最终发生了拉力支座的失效破坏。

2.5 翻转落梁

翻转落梁是整个支承体系超过了抗倾覆的临界点，桥梁发生了失稳的破坏，如图3、图4 所示。其原因多是超载车辆的偏载作用。除此之外，固结墩体系的自身强度不足，也有可能是发生落梁的原因之一。

图3 直线桥落梁

图4 曲线桥落梁

独柱曲线梁桥发生倾覆的主要原因是梁体在外部荷载作用下，超过了梁体自身的抗倾覆力矩。通常其过程可分为以下3 个阶段：

（1）当车辆荷载较小，其产生的倾覆力矩小于结构的抗倾覆力矩。此时各个支座正常工作，均未出现负反力，梁体处于稳定状态。

（2）随着荷载的增大，内侧支座出现了“脱空”等病害现象，支承体系随即发生变化，倾覆力矩与抗倾覆力矩相等。此时处于临界状态。

（3）荷载继续增大，倾覆力矩超过了抗倾覆力矩，此时结构发生失稳落梁。

因此，重视曲线梁桥的病害显现、分析病害诱因，将其遏制在萌芽状态显得尤为重要。配合全寿命周期，为曲线梁桥建立良好的健康档案、定期观测其位移量和反力变化，将大大有利于对桥梁稳定性的把控。

3 曲线梁桥倾覆轴的确定原则

研究结构的稳定性，最重要的一点是要根据支承体系确定结构的倾覆轴，根据自重、预应力和汽车荷载对倾覆轴的力矩大小确定结构的抗倾覆系数。因此，倾覆轴的确定是研究倾覆问题的关键所在。

倾覆轴应为“未脱空”的两支座的连线，其位置与支座的空间布置和箱梁半径有关，并遵循下列原则：

（1）当整个支承体系的全部支座均位于最外侧支座的连线以内时，倾覆轴线为外侧支座连线，如图5 所示。

图5 直线桥倾覆轴线

（2）当跨中的所有支座位于外侧支座连线以外时，倾覆轴线取为一外侧支座与跨中支座的连线或跨中支座之间的连线，如图6 所示。

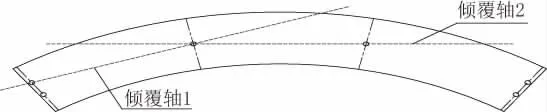
图6 曲线桥倾覆轴线

（3）同一座曲线梁桥的倾覆轴有可能不止一条，在进行抗倾覆分析时，需进行多工况的计算，从而选定最不利的倾覆轴。

4 计算分析

4.1 建立模型

以某工程三跨曲线梁桥为例，采用Midas Civil计算程序建模，重点考查预应力效应和自重效应等主要因素对结构产生的影响。同时，分析在活载效应下是否有加速结构倾覆的趋势，具体模型如图7、图8 所示。

图7 杆系模型

图8 杆系消隐模型

模型边墩采用抗扭性能较好的双支承，中墩采用多种支承计算比对，具体形式见表1。

表1 模型参数

4.2 结果分析

（1）方案一，倾覆轴如图9 所示。

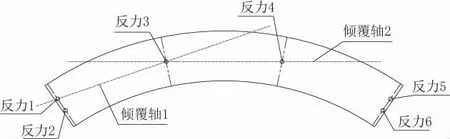
图9 方案一倾覆轴示意图

按照最不利荷载位置加载，曲线内侧支座出现了支座“脱空”。此时结构根据两条倾覆轴得到的抗倾覆系数分别为：K1=47.7、K2=15.1，此桥的抗倾覆系数为15.1＞2.5(规范值)。

（2）方案二，倾覆轴如图10 所示。

图10 方案二倾覆轴示意图

按照最不利荷载位置加载，曲线内侧支座仍出现了支座脱空，但其数值较小。此时结构根据三条倾覆轴得到的抗倾覆系数分别为：K1=48.4、K2=23.2、K3=85.0，此桥的抗倾覆系数为23.2＞2.5(规范值)。

（3）方案三，倾覆轴如图11 所示。

图11 方案三倾覆轴示意图

按照最不利荷载位置加载下，曲线内侧支座并未出现支座“脱空”。此时结构根据两条倾覆轴得到的抗倾覆系数分别为：K1=84.9、K2=36.6，此桥的抗倾覆系数为36.6＞2.5（规范值）。

通过计算分析，预应力效应、温度梯度效应和活载效应对曲线桥梁影响较大，在建模和分析中不可忽视。本例具有桥宽较宽、支承间距较小的特点，所以支座的反力在活载作用下显得十分敏感。实际设计时，推荐采用方案三的支承形式，以曲线内侧支座不出现负反力为控制原则，在中墩设置抗扭支承的双支座。

4.3 模型对比

考虑到不同的建模方式对结构受力的影响，本文根据方案三的支承条件，采用空间杆系单元和空间梁格单元两种方式进行验证，如图12、图13 所示。

图12 梁格模型

图13 梁格消隐模型

经过对比，通过梁格模型计算得到的结果比杆系模型不均匀性表现得更明显。所以，计算小半径曲线梁桥时，建议采用梁格模型；计算大半径曲线梁桥及直线梁桥时，可采用简化的杆系模型，从而提高计算的效率。

综上所述，对于独柱曲线梁桥，通过建立合理的空间计算模型，并运用稳定性理论和相关的抗倾覆系数计算公式，能够直观地把握各个支承体系下的结构安全状况。

5 曲线梁桥抗倾覆对策

虽然独柱曲线梁桥的稳定性受到诸多因素的影响，但可以根据工程经验和设计验算制定多种对策，从其设计伊始，为其打造具有良好稳定性的结构体系。

5.1 合理稳定的支承体系加大抗扭能力

（1）除在梁端设置抗扭支承外，在中墩尽量采用固结或双支承等抗扭支承形式，以加大结构自身的抗扭性能，提高其稳定性。

（2）在条件允许的情况下，可以将横梁外延而加大支承间距，增大桥宽与边支座间距比，从而降低曲线内侧支点出现负反力的发生几率。

5.2 合理的偏心距设置调节扭矩分布

（1）将中墩支座或者双支承设置横向（曲线外侧）预偏心，提高梁端抗扭性能，防止支座“脱空”。

（2）对于大曲率的曲线梁桥，设置偏心效果甚微，可通过增加配重混凝土的方法消除支座负反力。

5.3 增加结构的抗扭刚度

加强横梁和横隔板构造设计，从而提高结构的抗扭性能，降低曲线内外侧腹板的受力差异。

5.4 完备的构造设施保障

（1）设置限位措施，有效限制曲线梁桥的径向位移。

（2）增设必要的防落梁措施，提高梁体的稳定性。

6 结语

近年来，独柱曲线梁桥被更多地应用于城市和公路立交建设中，关注结构的整体稳定性成为独柱曲线梁桥设计的重中之重。本文旨在通过对结构受力和典型病害的剖析，参考相应的稳定计算方法，合理的建模并实例分析，从而得出一些建议，为类似工程的设计提供思路和指引。