基于SFS 方法的侧扫声呐图像三维重构

刘浩林，覃珊珊，李鹏鸽，张晓晖，刘青

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

0 引言

侧扫声呐效率高及价格低，尤其具有高分辨率的特点，是海洋开发，海底地形勘察，考古调查等行业领域的有力工具[1]。然而，因其工作原理制约，其获取的声呐图像无法直观得到被测区域高度信息。为解决这一问题，国内外学者在声呐图像的三维重构方面展开了大量研究，并取得了一些成就[2–3]。

明暗恢复形状（Shape from shading,SFS）方法为海底地形三维重构提供了思路，它可利用图像的明暗变化来获取物体表面的相对高度[4]。该方法有最小化法、演化法、局部分析法及线性化法4 种。其中最小化法为多数文献公认鲁棒性及抗噪性较好的一类[5–6]。最小化法最开始由Horn 等[7]提出，将SFS 问题描述为一个能量函数，并加入光滑性约束。Zheng[8]并没有用光滑性约束条件，而采用图像梯度约束，从而消除光滑约束的局限性。在此基础上，Johnson 等[9]为了保证最终的物体表面的相对高度连续可积，提出了图像可积性约束。之后，Leclerc 和Bobick[10]提出了离散化的直接重构物体表面相对高度的迭代算法。然而，现有的SFS 最小化方法是在所研究的对象为光滑表面的假设上提出的，对于实际的侧扫声呐图像的恢复精度不高。

为此，本文从侧扫声呐工作原理出发，首先对侧扫声呐原始数据进行解码及可视化研究，然后利用小波变换对SFS 最小化方法进行改进，对侧扫声呐二维瀑布图进行三维重构，实现海底地形反演，并对反演结果进行分析。

1 侧扫声呐工作原理

侧扫声呐工作时声呐探测装置安装在拖鱼上，声呐发射阵列会沿垂直于拖鱼前进方向的一侧或两侧发射一束垂直开角很大但水平开角很小的声波脉冲，脉冲遇到海底表面或者水下物体被不断反射，可按反射信号的强弱程度画出灰度变化不均的声呐图像[11]。图1为侧扫声呐的工作原理示意图。

图1 侧扫声呐工作原理示意图Fig.1 Schematic diagram of the working principle of side scan sonar

从声呐图像中可以观察出海底地貌变化，是否有碍航物和海底底质类型等信息。对于凸起、坚硬或者粗糙的海底区域，一般反射回波信号强；反之，凹陷、细软或平缓的海底表面反射回波信号弱，而被遮挡的海底表面不会产生反射回波信号，距离越近的海底反射回波信号越强[12]。

2 原始数据解析

现有的大部分侧扫声呐原始数据处理软件与声呐设备捆绑，也有少数是国外的商业软件，如Sonar WaveLite 软件等，但由于软件侧重的功能不同，缺乏侧扫声呐全部参数提取及解析功能，不能满足海洋地质调查的需求[13–14]。

本文选用C++作为数据解析系统的开发语言，利用opencv 作为图像处理工具，在Visual Studio 2015 中实现了侧扫声呐XTF 格式原始数据文件的信息提取及可视化，其程序流程图如图2 所示。

图2 XTF 文件数据解析流程图Fig.2 XTF file data analysis flow chart

可视化程序部分利用opencv 视觉库的函数分别对通道数据中的声呐回波强度信息进行提取，并将其赋值给灰度图像矩阵，进行声呐瀑布图显示，如图3（a）所示。同时为了方便对结果进行验证，在生成图像时进行反色运算，如图3（b）所示。为验证程序的准确性，将本文解析软件结果与国外软件SonarWaveLite 得到的侧扫声呐瀑布图进行比照，对比图如图4 所示。其中图左为国外软件生成的图，图右为程序运行结果图。

图3 侧扫声呐瀑布图Fig.3 Side scan sonar waterfall chart

图4 侧扫声呐瀑布图对比图Fig.4 Side scan sonar waterfall chart comparison

由于国外软件会对原始瀑布图进行简单图像处理后再显示，如图像增强等操作，所以相较于程序运行结果图对比度会较强，但是2 张图片的基本灰度变化趋势是相同的，由此可验证程序的有效性。

3 侧扫声呐图像三维重构

在侧扫声呐的三维重构部分，本文提出了基于小波变换的SFS 最小化算法，二维图像在经小波分解后的低频部分采用了基于Priwitt 算子的三维重构算法，而在图像的高频部分很好地利用了SFS 最小化方法的优势。实验表明该方法有效可行，且恢复结果的精度得到提高。

3.1 图像的小波变换

利用小波的的多分辨率特点，可以对图片进行分解及重构，如图5 所示。其中图像分解时，首先对图像进行行分解，获得图像在水平方向上的低频分量L 和高频分量H，然后在其基础上再进行列分解，最终获得一个低频分量LL 及LH，HL 和HH 三个高频分量图像。图像重构时，首先对分解结果的每一列进行一维离散小波逆变换，再对所得数据的每一行进行一维离散小波逆变换，即可获得重构图像。

图5 图像的二维离散小波分解和重构过程Fig.5 Image decomposition and reconstruction process of two-dimensional discrete wavelet

小波变换用于图像分解时，最重要的就是小波基的选择。同一幅图像，用不同的小波基进行分解得到的效果都是不一样的。本文选择文献[14]中提到的具有良好平滑性的小波基db2，来实现高质量的图像分解及重构。

3.2 基于Priwitt 算子的三维重构算法

对于小波变换后低频部分图像的处理，本文提出基于Priwitt 算子的重构算法。首先利用Priwitt 算子计算海底表面每一点的法矢向量，然后利用数值积分计算海底表面点的三维高度值，并利用双线性插值得到海底表面点更精确的高度信息。

3.2.1 表面法式的计算

海底表面法矢可以通过表面的倾角和偏角计算得到。

声波脉冲入射方向可以用单位向量表示如下：

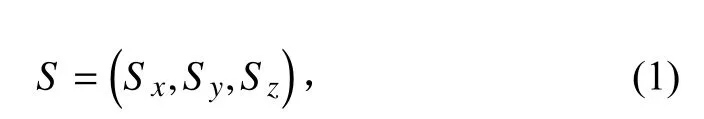
N(x,y)为像素点l(x,y)处的法向单位向量，其可表示如下：

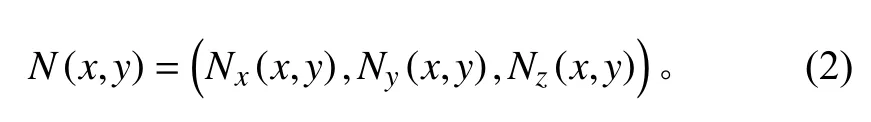
SFS 方法普遍假设入射光为无限远处点光源，即S=(0,0,−1)，且物体表面反射模型为朗伯模型[4]，由朗伯模型可知海底某一点l的反射强度值E(x,y)由海底表面反射率 ρ、声源强度值E0及倾角 θ的余弦值决定，即

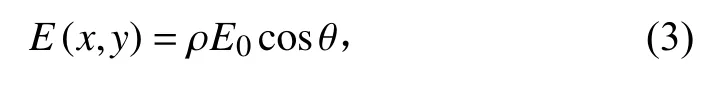
海底反射模型几何关系如图6 所示，倾角 θ是法向量N和入射向量S的夹角。

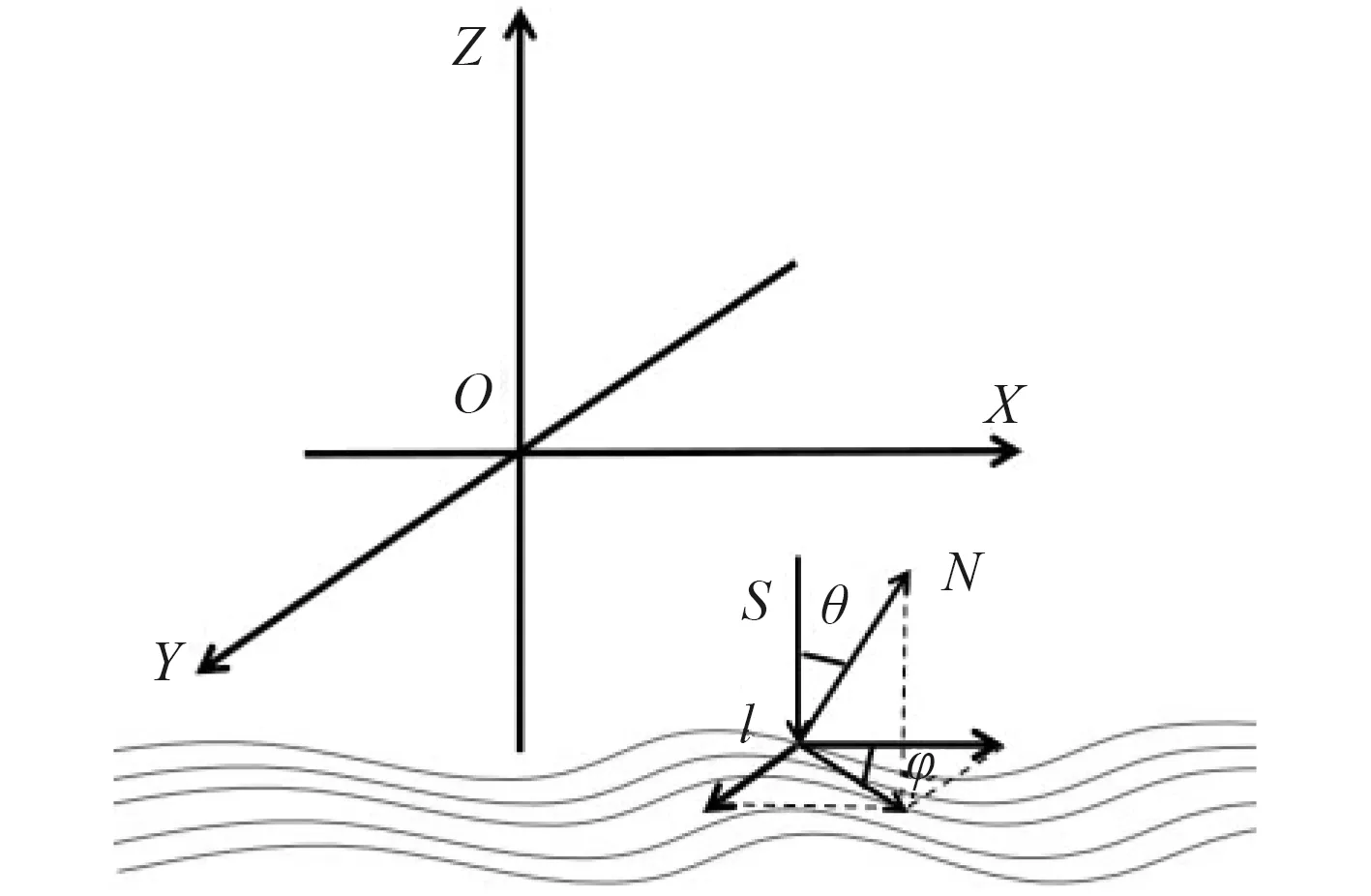
图6 海底反射模型几何关系Fig.6 Geometric relationship of seabed reflection model

式（3）中，ρ及E0一般是常数，因此可以把E(x,y)归一化为：

由式（4）可得出倾角的计算公式为：

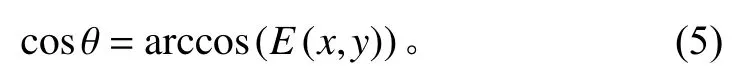
从图6 可看出，偏角 φ为海底表面法线矢量N在xoy平面的投影与x轴的夹角。而瀑布图像中灰度梯度方向为海底表面法线投影的方向，所以可通过灰度梯度来计算海底表面法线矢量。

通常，在点(x,y)处的灰度E(x,y)的梯度值为一个二维列向量，定义如下：

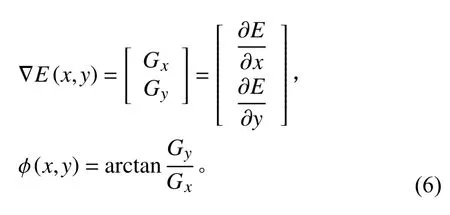
式中，Gx和Gy分别为E(x,y)在x方向和y方向的1 阶偏导数。其中，偏导数的计算可以用可以用差分运算来表示。Priwitt 算子就是基于差分运算的一个梯度算子，其水平和垂直梯度算子的模板如图7 所示。

图7 Priwitt 算子（8 邻域3×3）Fig.7 Priwitt operator (8 neighborhood 3×3)

对于图中的任一点 (i,j)，利用Priwitt 算子对每一像素点相邻8 个像素进行加权运算，分别得到该像素点在x方向和y方向的梯度，表达式为：

在利用式（7）计算出各个点的梯度后，根据式（6）即可以计算得到偏角 φ的值。

由图6 中几何关系，N(x,y)可表示为：

至此，可以计算得到所有点的表面法矢向量N(x,y)的值。

3.2.2 数值积分

在获得了瀑布图像的各个表面点的表面法矢向量N(x,y)的值后，还需根据N(x,y)计算海底表面的高度值z(x,y)。本文利用数值积分运算来计算z(x,y)的值。

本文采用牛顿-柯特斯公式的梯度变形公式来计算积分。设[a,b]为一个有限区间，有

由于海底表面能够用含有表面高度信息的方程z=f(x,y)表示，且表面梯度p和q又可以由下式表示：

根据式（10）可得到z的积分表达式：

式中，z0表示参考点 (x0,y0)处的深度值，结合式（10）所示的数值积分，最终计算出z值。

在一般的离散数据计算中，获得的数据不具有连续性，因此本文采用双线性插值的方法，来获得除了离散点处函数值以外的更多数据。

3.2.3 基于小波变换的SFS 最小化方法

本文提出的基于小波变换的SFS 最小化方法步骤如下：

1）将二维瀑布图像经小波二次分解后得到1 个低频子带LL 和3 个高频子带。

2）在图像的低频部分采用基于Priwitt 算子梯度算法，计算出这部分物体表面三维高度值。

3）在图像的3 个高频部分采用文献[10]中经典最小化方法迭代求解，计算出对应点的高度值。

4）将第2 和第3 步得到的实验结果结合起来，恢复出物体表面三维形状。

3.3 实验结果比较与分析

利用对比实验对本文提出的基于小波变换的SFS 最小化算法进行验证分析。

3.3.1 实验说明

本文关于三维重构算法的评价标准采用2 种方式：

1）视觉效果

以三维重构的图形结果作为SFS 算法的评判标准，主要是水下物体的恢复形状、海底表面纹路是否清晰及高度起伏是否明显。

2）量化表示

本文为评价SFS 算法在三维重构中的效果，将重构结果利用朗伯反射模型投影得到对应的平面灰度图。再将其与原始输入图像利用平均绝对误差（MAE）、相关系数（CC）及平均结构相似性（MSSIM）3 个评价指标进行图像相似性分析。其中，MAE的值越小，表明图像之间的误差越小，图像相似度也越高。相关系数的绝对值|CC|越接近于1 时，图像相关程度越好。MSSIM 越接近1，则2 张图像越相似。

3.3.2 验证实验结果

以Imagenex SportScan 侧扫声呐实测图像中截取的部分左舷图像数据为例，大小为446×376像素，利用文献[7]和文献[10]提出的2 种经典SFS 最小化算法及本文提出的算法进行对比实验，得到三维重构结果如图8 所示。

分别将三种重构结果进行投影，在朗伯反射模型下得到对应的平面灰度图，如图9 所示。

将图9 中三维结构对应的平面灰度图像与原始输入图像进行相似度对比分析，得到的分析结果如表1所示。

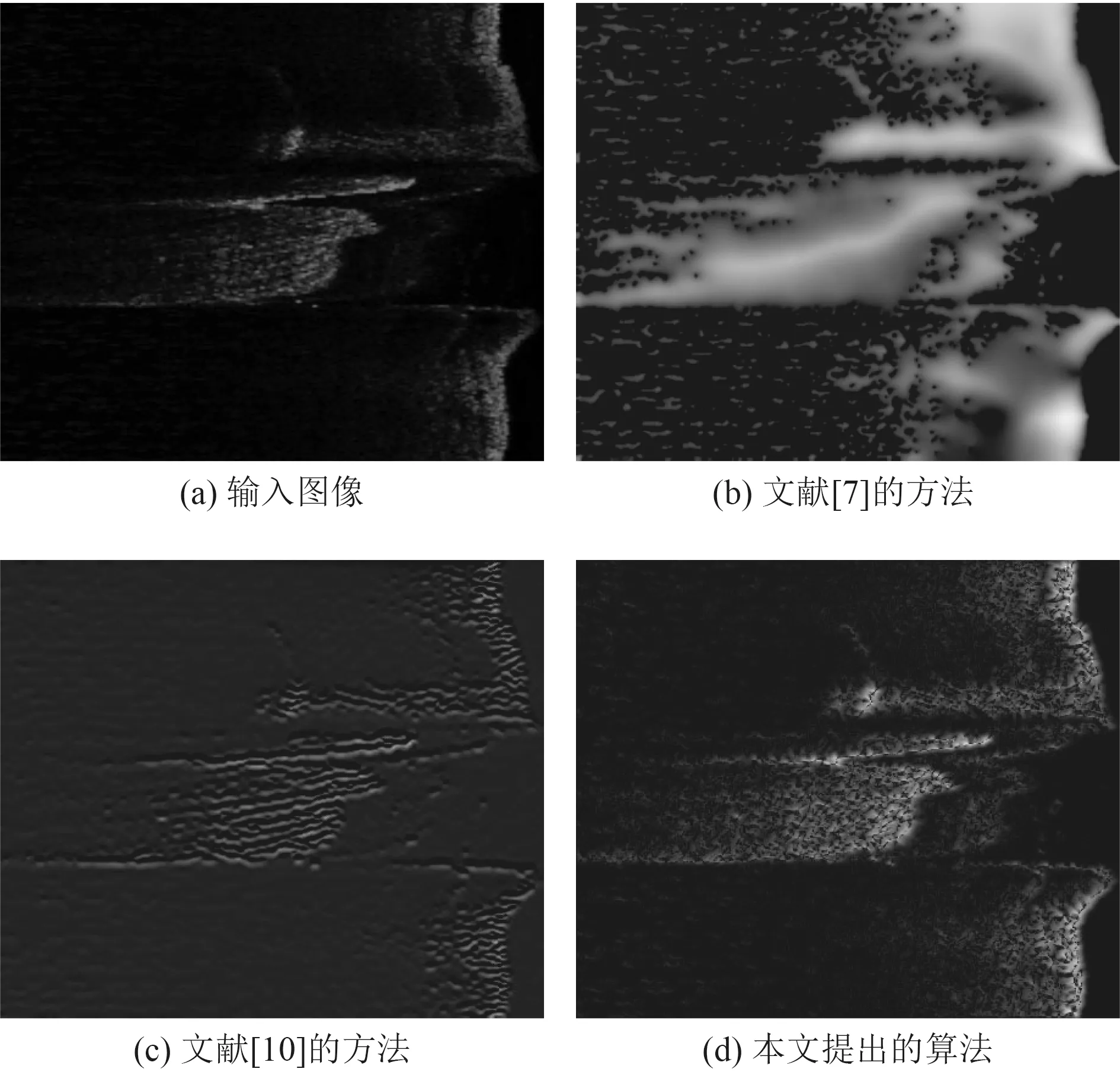
图9 侧扫声呐实地测试图像的三维重构Fig.9 Three-dimensional reconstruction of field test images of side scan sonar

从图8 可以观察到，从视觉效果来看，对于侧扫声呐实测图像，本文提出的算法恢复效果最好，三维重构图可清楚显示海底表面高度波动以及水下地形的细微特征。而文献[10]的算法效果次之，文献[7]的算法最差。从表1的评价指标可看出，本文提出的算法与输入图像间的MAE 值最小，表明两图像之间的绝对误差相对较小。本文提出算法得到的对比图像间CC 及MSSIM 值相比之下是最接近于1的，说明图像间相似度之高，即本文提出算法的三维重构结果精度高。

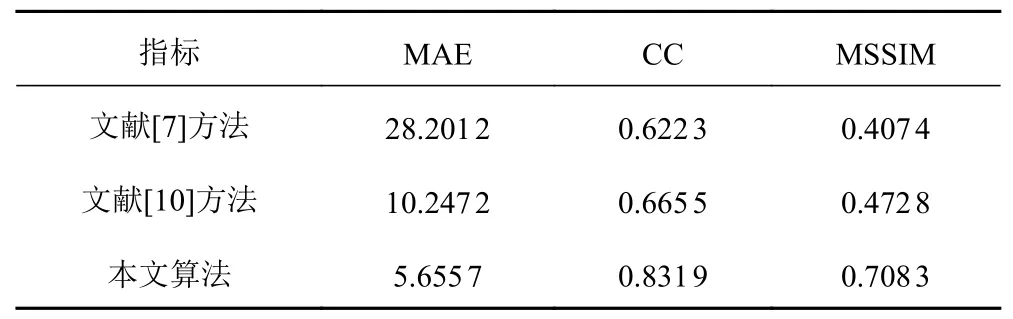
表1 重构结果对应的平面灰度图评价指标对照表Tab.1 Corresponding table of evaluation indexes of plane gray image corresponding to the reconstruction results

图8 侧扫声呐图像的三维重构结果图Fig.8 The 3D reconstruction result of the side scan sonar image

4 结语

本文首先深入了解侧扫声呐工作原理及作业模式，在此基础上，利用Visual Studio 平台实现对XTF 格式原始数据进行解析，获取各种有效信息及回波强度值，利用opencv 工具实现侧扫声呐二维瀑布图的可视化，获得了理想的结果。利用小波变换对SFS 最小化法进行改进，以二维瀑布图作为输入，实现了海底地形的三维重构。最后通过对比实验对本文提出的算法进行分析，结果表明，与2 种经典的SFS 算法相比，基于小波变换的SFS 最小化法性能明显提高，可清晰显示海底表面起伏变化和水下地形的细微特征，从而验证了算法的有效性及准确性。