几个局部分数阶积分不等式与广义矩的有界估计

2021-09-17郑爱民孙文兵

浙江大学学报（理学版） 2021年5期

郑爱民，孙文兵

郑爱民1，孙文兵2*

（1.邵阳学院会计学院，湖南邵阳 422000； 2.邵阳学院理学院，湖南邵阳 422000）

局部分数阶微积分在数学、力学工程、物理等领域有非常广泛的应用，如应用于分形热扩散和振子等微分方程数学模型的计算与分析［1-4］。YANG［5］介绍了Yang分形集理论和局部分数阶微积分理论，在此基础上，文献［6-12］以局部分数阶微积分为研究工具，对许多著名的积分不等式进行了推广研究。

SARIKAYA等［13］建立了Yang分形集上的广义Čebyšev型不等式。

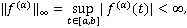
则

其中，

SARIKAYA等［6］证明了以下的局部分数阶积分恒等式并建立了Yang分形集上的广义Ostrowski型不等式。

其中，

定理3（广义Ostrowski型不等式）若定理2条件满足，则有

1预备知识

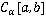
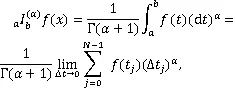
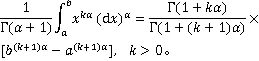
2主要结果及证明

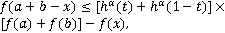
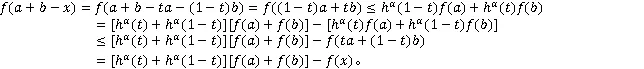
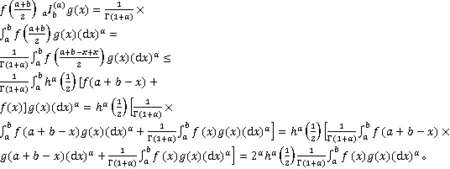
由引理3，可得

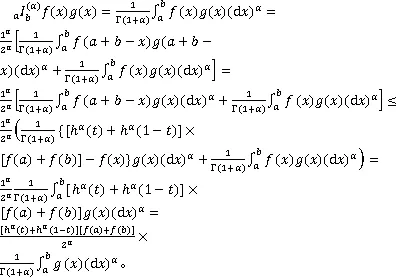
由式（7）和式（8），可知结论成立。

定理4证毕。

显然结论成立。

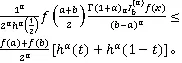
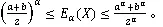
则有

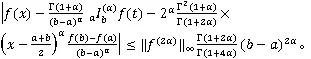
证明取

则

由广义Čebyšev型不等式，可知

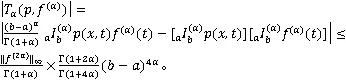
由广义Montgomery恒等式，可知

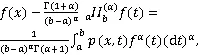
经计算可得

将式（16）～式（18）代入式（15），整理后可得式（14）。

定理6得证。

注2 称定理6为广义Ostrowski-Čebyšev型不等式。

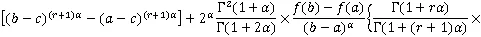
（19）

证明由定理6广义Ostrowski-Čebyšev型不等式，可得

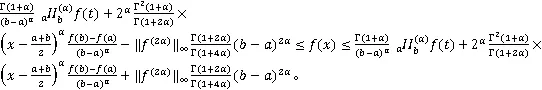
经计算可得

且

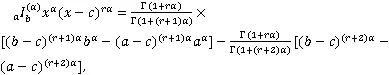
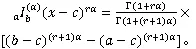
将式（22）～式（24）代入式（21），可得式（19）。

定理7得证。

［1］HEMEDA A A， ELADDAD E E， LAIRJE I A. Local fractional analytical methods for solving wave equations with local fractional derivative［J］. Mathematical Methods in the Applied Sciences， 2018，41（6）：2515-2529.

［2］YANG X J， BALEANU D. Fractal heat conduction problem solved by local fractional variation iteration method［J］. Thermal Science， 2013，17（2）：625-628. DOI：10.2298/tsci121124216y

［3］YANG X J， MACHADO J A T， BALEANU D， et al. On exact traveling-wave solutions for local fractional Korteweg-de Vries equation［J］. Chaos， 2016， 26 （8）： 084312. DOI：10.1063/1.4960543

［4］YANG X J， MACHADO J A T， SRIVASTAVA H M. A new numerical technique for solving the local fractional diffusion equation： Two-dimensional extended differential transform approach［J］. Applied Mathematics and Computation，2016， 274： 143-151. DOI：10.1016/j.amc.2015.10.072

［5］YANG X J. Advanced Local Fractional Calculus and Its Applications［M］. New York： World Science Publisher， 2012.

［6］SARIKAYA M Z， BUDAK H. Generalized Ostrowski type inequalities for local fractional integrals［J］. Proceedings of the American Mathematic Society， 2017，145（4）： 1527-1538.

［7］MO H X， SUI X， YU D Y. Generalized convex functions on fractal sets and two related inequalities ［J］. Abstract and Applied Analysis， 2014， Article ID 636751. DOI：10.1155/2014/636751

［8］MO H X， SUI X. Generalized s-convex functions on fractal sets［J］. Abstract and Applied Analysis， 2014， Article ID 254731. DOI：10.1155/2014/254737

［9］SUN W B. Generalized harmonically convex functions on fractal sets and related Hermite-Hadamard type inequalities［J］. Journal of Nonlinear Sciences and Applications， 2017，10（11）： 5869-5880. DOI：10.22436/jnsa.010.11.24

［10］孙文兵，刘琼. 分形集上广义凸函数的新Hermite-Hadamard型不等式及其应用［J］. 浙江大学学报（理学版）， 2017，44（1）：47-52. DOI：10.3785/j.issn.1008-9497.2017.01.007

SUN W B， LIU Q. New inequalities of Hermite-Hadamard type for generalized convex functions on fractal sets and its applications［J］. Journal of Zhejiang University（Science Edition），2017，44（1）： 47-52. DOI：10.3785/j.issn.1008-9497.2017.01.007

［11］VIVAS M， HEMANDEZ J， MERENTES N. New Hermite-Hadamard and Jensen type inequalities for-convex functions on fractal sets［J］. Revista Colombiana de Matematicas， 2016，50（2）：145-164. DOI：10.15446/recolma.v50n2.62207

［12］SUN W B. Generalized-convexity on fractal sets and some generalized Hadamard type inequalities［J］. Fractals， 2020， 28（2）： 2050021.

［13］SARIKAYA M Z， TUNC T， BUDAK H. On generalized some integral inequalities for local fractional integrals［J］. Applied Mathematics and Computation， 2016，276：316-323. DOI：10.1016/j.amc.2015.11.096

Some local fractional integral inequalities and bounded estimates of generalized moments

ZHENG Aimin1, SUN Wenbing2

(1422000;2422000)