短期风电出力预测方法研究
2021-09-17王康亓孝宇
王康,亓孝宇
(1.山东正晨科技股份有限公司,山东济南,250101;2.山东诺安诺泰信息系统有限公司,山东济南,250101)
0 引言
风电作为一种典型的清洁能源,其在电网中的渗透率逐步提升,对电网的运行方式的影响也逐渐增大[1]。风力发电的原动力来自风能,因此其本质中具有功率输出的随机性和波动性,这两种特性给电网的调度和经济运行带来一定挑战,也给传统运行方式下的电力系统功角稳定、频率稳定、电压稳定带来一定程度的负面效应[2-4]。
风电出力预测可以给系统机组组合、机组出力、备用容量选择提供前瞻性的指导,提高系统运行的稳定性和经济性。风电出力预测可以降低风电本身的随机性限制,从一定的时间尺度上增大其可控性,为其无功投入、桨角控制等提供信息[3]。此外,风电出力预测可以给设备的运维提供信息,指导合理安排设备的检修计划,提升设备的健康程度和延长设备寿命[5]。
当前针对风电出力的预测研究较多,根据时间尺度可分为;超短期预测、短期预测中、长期预测[6]。短期风电出力预测以小时为时间尺度,多应用于调度优化。短期风电出力预测根据预测原理分为物理方法和统计方法,物理方法基于数值天气预报中的气压、气温、风向等信息,采用微气象学理论或流体力学计算方法开展,需要数据量大,计算过程较为复杂,且针对不同环境的风电场,其物理描述区别较大,推广性不好[7];统计方法基于大量的历史数据,采用算法挖掘历史数据信息,对未来的出力进行预测,该类算法需要的数据量较大,且由于风速自身特性和模型参数的不确定性,预测误差的控制仍需进一步优化[8-9]。
1 模型建立
■1.1 模型的基本结构
建立基于Bootstrap方法和KELM的风电功率区间预测模型,模型的结构如图1所示。首先采集风电出力训练数据集D,然后利用Bootstrap方法采样得到K个子训练集,训练K个KELM模型,计算其均值及方差,根据各数据点残差值构造训练集,训练一个KELM对噪声方差进行估计,最后根据预测均值、模型估计方差和噪声估计方差计算预测区间。
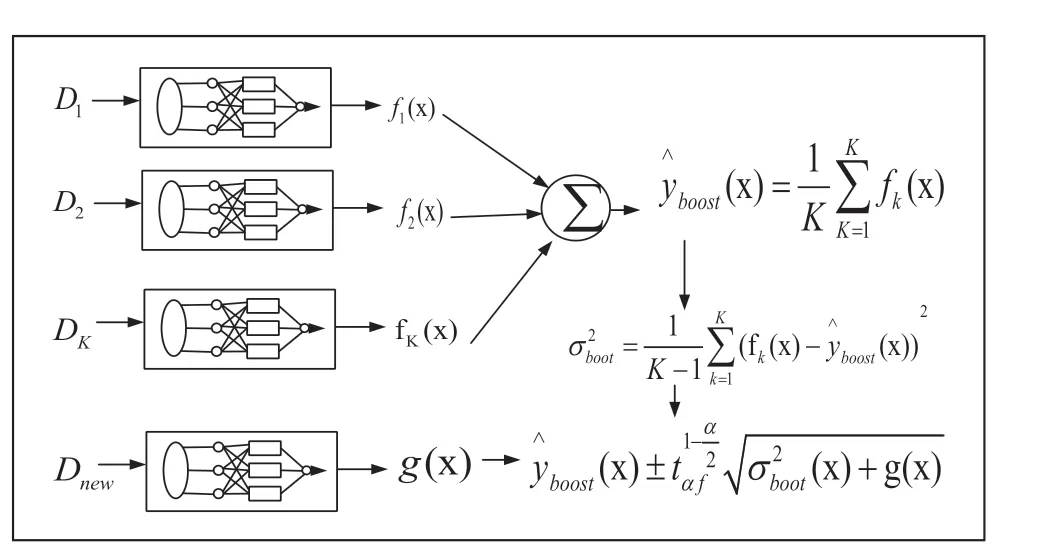
图1 基于Bootstrap方法和KELM的风电功率区间预测模型结构
本文实际获取了内蒙某风电场的实际运行数据,并综合考虑模型的复杂程度,选取对风电出力影响较大风速、风向作为KELM的输入数据。其中,风向以标准的地图坐标(上北下南)为坐标系,单位长度的余弦值和正弦值表示,因此,输入数据包含了风速、风向余弦值、风向正弦值三个维度,输出数据为实际风电出力。
■1.2 模型预测步骤
模型的预测步骤如下:
STEP1 选取风电场SCADA数据,归一化至[0,1]区间,并划分训练集和预测集;
STEP2 对原始训练集进行K次有放回的采样,得到K个子训练样本集;
STEP3 采用原始训练集数据,运用PSO算法对K+1个KELM模型的核参数γ和惩罚系数C进行优化;
STEP4 使用子训练样本训练K个KELM模型,计算K个KELM模型在训练集上的预测均值和方差;
STEP5计算得到噪声方差预测模型的训练数据,并训练得到第K+1个KELM模型;
STEP6 对预测集进行预测,将K个KELM模型的预测平均值作为点预测结果;根据式计算在(1-α)% 置信水平上的顶层油温预测区间,对预测结果进行反归一化处理。
2 算例分析
■2.1 数据预处理
为验证本文所提出模型的有效性,获取内蒙某风电场在2016年6-9月间SCADA风电功率数据和风电场风速、风向记录数据,数据时间尺度为15分钟/组。经数据预处理后,识别、剔除明显错误数据并采用二阶插值法修复缺失数据。共得到8518组数据,选取前8338组数据作为训练集,后180组作为预测集。对初始训练集进行K=30次有放回的随机采样,共得到K=30个子训练集,部分数据如表1所示。

表1 部分风电场数据
对样本数据按式(1)进行归一化处理:

其中smin和smax分别为各变量的极小值和极大值。
■2.2 模型评价指标分析
风电出力预测区间的评价指标可以从可靠性和清晰度两个方面来衡量。可靠性表征预测区间覆盖真实值的能力,本文以预测区间覆盖率(PI coverage probability, PICP)来衡量。清晰度表征预测区间的质量,本文以平均预测区间平均宽度(Mean PI Width, MPIW)来衡量。PICP和MPIW如式(2)所示:

其中Ui和Li分别表示预测区间上限值和下限值。Ntest为测试样本个数;ci为布尔量,若预测区间覆盖目标值,则ci=1,反之ci=0。
在风电出力预测当中,PCIP必须大于或接近置信水平,即必须保证预测区间足够大的覆盖率,才能保证预测的有效性。在保证预测区间有效性的前提下,越小的MPIW代表预测区间宽度越窄,预测结果的清晰度越高。
■2.3 模型参数优化
首先设置PSO算法参数,加速因子c1=c2=2, w=0.65,种群数量为30,最高迭代tmax=200次。在KELM算法参数优化过程中,PSO算法快速、可靠收敛,最终求得K个KELM模型的参数优化结果为 [γbest, Cbest]=[1.45, 0.69],第K+1个噪声方差KELM模型的参数优化结果为[γbest,Cbest]=[1.29, 0.71]。K个KELM模型的参数优化过程中,适应度函数收敛曲线如图2所示。
由图2可以看出,当迭代次数大于60次时,适应度函数不再改变,PSO算法求得全局最优解。

图2 PSO算法寻优过程适应度收敛曲线
■2.4 模型预测结果分析
短期风电预测对于风电入网安全性至关重要,因此预测结果的可信度十分重要。本文分别预测了95%置信度、90%置信度和80%置信度下的预测集区间上下限值,并与实际风电功率进行对比,预测结果分别如图3、图4、图5所示。
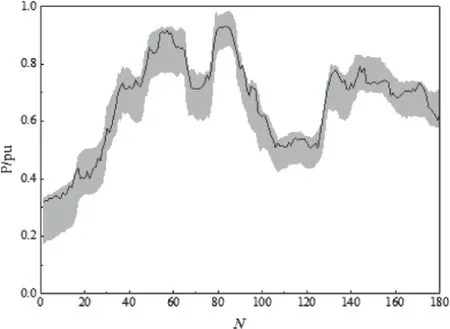
图3 95%置信水平下风电功率预测区间

图4 90%置信水平下风电功率预测区间
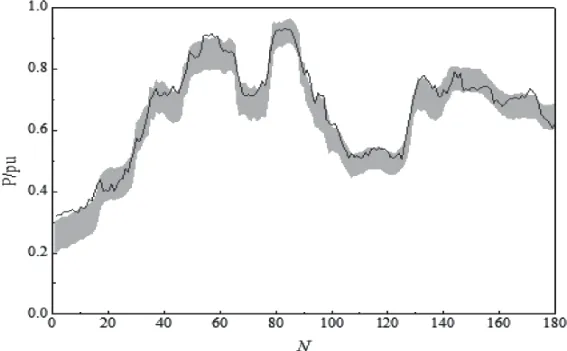
图5 80%置信水平下风电功率预测区间
由图3可以看出,在95%置信水平下本文所提模型的预测区间可以完全覆盖风电功率实际值,由图4和图5可以看出,在80%-90%置信水平下,本文所提模型均可以较好的覆盖风电功率实际值,只有极少数实际功率点落在了预测区间以外。置信水平越高,预测区间宽度越大,预测区间覆盖率越高,但是预测区间平均宽度越大,预测区间的清晰度降低。不同置信水平下,预测指标对比如表2所示。

表2 不同置信水平下区间预测指标
由表2可以看出,95%置信水平下的预测区间覆盖率为100%,80%-90%置信水平下,预测区间覆盖率均大于置信水平,能够为调度决策者提供有效信息。调度决策者可以根据实际需求,选择不同置信水平下的预测区间。
3 结论
本文所提区间预测模型在80%-95%置信水平上可以给出风电功率预测区间,且预测区间具备较好的清晰度。本文所提区间预测模型可以提供给调度决策者预测功率的保守值和乐观值,相比于点预测模型,可以提供更为丰富的参考信息。PSO算法能够快速可靠实现KELM模型参数寻优。
