基于引力搜索机制的数据聚类及特征选择算法

张雪峰，杜孝平，王晓健，王 哲

(1.北京赛迪工业和信息化工程监理中心有限公司 信息化管理与咨询部，北京 100048；2.北京航空航天大学 软件学院，北京 100191；3.湘潭大学 信息工程学院，湖南 湘潭 411105)

0 引 言

数据聚类是将未标记数据集分割为相似数据点群组，每个群组为一个聚类，其内的数据点具有最大相似性，而不同聚类间数据点差异较大[1]。数据聚类在图像分割[2]、机器学习[3]、文本分析、模式识别[4]等方面得到了广泛应用。目前数据聚类方法有两类：分层式方法和分割式方法。分层式方法的主要不足是：①静态属性，即数据点的移动受限于分配的所属聚类内；②重叠聚类无法分离。分割式方法旨在将数据划分为不相交聚类集，该方法也是本文采用的聚类方法。

多数分割聚类方法在聚类过程中给予所有特征相同重要性。但部分特征实际是不相关或冗余的，这在处理高维度数据集聚类时尤其无法得到较好聚类结果[5]。因此，有必要选择使数据聚类更适宜的相关特征。此外，获得最优聚类数量也是分割聚类的另一挑战。求解数据聚类问题必须同步选择相关特征和最优聚类数量[6]。为解决该问题，本文利用引力搜索机制设计一种自动式聚类和特征选择算法。算法试图在没有聚类数量先验知识前提下，同步决策聚类数量和相关特征。设计了一种复合代理表示方法，用于分别对聚类和特征进行编码。同时，设计了一种临界值概念用于寻找最优聚类数量和特征。最后通过9种数据示例集测试验证了算法的有效性和可行性。

1 相关工作

本小节同时对特征选择和聚类问题的相关工作做概述性研究。K-means算法是最早的一种经典数据聚类算法[7]，由于其最终解过多依赖于初始的质心选择，因此较容易存在严重的局部最优情况。文献[8]提出一种基于改进和声搜索的聚类算法，将状态反馈机制引入到和声搜索算法中，通过判断和声记忆库中最优和声和最差和声之间的差异来动态调整和声记忆库考虑概率和移动步长，使算法能够快速地收敛到全局最优解。文献[9]提出一种基于蚁群优化思想的聚类和特征选择算法FS_ACO。算法使用了基于包装的思路，并利用连续回溯选择技术实现特征提取。文献[10]提出基于粒子群优化的数据聚类和特征选择算法CFS_PSO。文献通过随机化特征选择机制改进了粒子群的搜索行为，以此选择相关特征，而聚类解则在所选特征的基础上进行迭代求解。文献[11]提出一种模因算法NMA_CFS寻找数据聚类和特征选择解，利用了局部搜索机制在编码染色体中提炼数据聚类，但种群多样性的不足使得算法会出现早熟，从而收敛在局部最优解上。文献[12]设计了一种自冶的和声搜索聚类算法HS_CFS，算法针对模糊聚类对初值和聚类中心的依赖性，采用和声搜索寻找最佳聚类质心，并且改进了和声搜索的调音概率和随机带宽，加速了算法收敛。文献[13]则提出改进文化基因聚类算法INMA_CFS，首先，基于特征与标记间的依赖将特征按照适应度进行排名，使用遗传搜索建立多标记类；然后使用局部优化方案向被选的特征集中增加精英样本或删除较弱样本。对部分基因进行改良，且在搜索过程中逐渐改变优化操作的次数，从而降低了整体计算成本。以上算法并没有考虑到数据集的变异特征，该特征是一种统计属性，且极大取决于数据点及其特征的数量。而数据聚类数量又直接或间接地取决于特征数量，给定数据集,其冗余特征可能影响聚类性能。因此，识别和寻找相关特征对于数据聚类过程具有关键影响。

以上研究概述表明元启发式方法是选择数据特征和同步数据聚类的有效手段，但以上方法并没有考虑到数据集的变化特点(统计属性)，该属性直接取决于特征选择的数量和数据点。而聚类数量直接或间接取决于特征数量，在给定数据集中的冗余特征可能一定程度上会影响聚类算法的性能。因此，尽可能选择相关特征剔除冗余特征是至关重要的。鉴于引力搜索算法所依赖的初始参数数量较其它智能群体算法更少，选择该算法作为特征选择和聚类的优化手段将具有一定可行性。

2 数据聚类与引力搜索模型

2.1 数据聚类模型

(1)每个聚类拥有至少一个数据点，即Cg≠∅,g=1,2,…,K；

(2)两个不相似的聚类不存在共同的数据点，即Cg∩Ch=∅,g,h=1,2,…,K，且g≠h；

数据点是否属于某一个特定聚类内取决于其相似性，该相似性通常以数据点与聚类中心的欧氏距离度量。数据点xl与聚类Cg的聚类中心mg的欧氏距离定义为

(1)

2.2 引力搜索算法模型

引力搜索算法GSA[14]是基于万有引力和物体质量间的相互影响发展来的一种元启发式算法。GSA中，给定问题的可能解考虑为代理集合，代理的质量决定代理的性能。由于引力的影响，代理之间会相互吸引，导致代理会朝着拥有更大质量的代理进行全局移动。问题的解即对应于代理在空间中的位置，适应度函数则决定了代理的惯性质量。GSA的执行步骤如下：

步骤1 代理初始化。随机初始化P个代理位置为

(2)

步骤2 适应度评估，计算最优适应度。对于所有代理，计算每次迭代中的适应度。最优和最差适应度的计算方法为(对于最大化问题)

(3)

(4)

其中，fitnessi(T)表示代理i时刻T的适应度，Best(T)和Worst(T)分别表示时刻T所有代理中的最优适应度和最差适应度。

步骤3 计算引力常量。时间t时的引力常量表示为Gc(t)，定义为

(5)

式中：G0和α为常量，Tmax为最大迭代次数。

步骤4 计算代理的引力质量。时间T时代理i的引力质量表示为Massi(T)，基于当前种群的适应度进行计算

(6)

其中

(7)

步骤5 计算代理引力和加速度。时间T时在维度D上代理i受到代理j的引力定义为

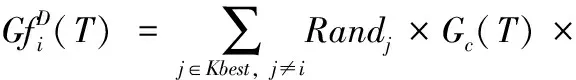
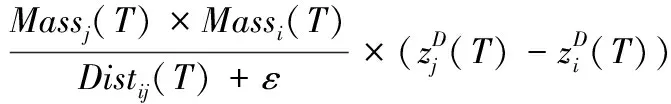
(8)

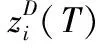
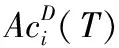
(9)

步骤6 代理位置和速度更新。下一迭代T+1时代理的位置和速度可计算为

(10)

(11)

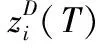
步骤7 终止条件。重复步骤2～步骤6，直接迭代过程达到最大迭代次数为止。

3 算法详细设计

本节的主要工作是设计一种基于引力搜索机制的数据聚类与特征选择算法。首先，提出一种变量合成代理表示策略使得算法可以同步寻找最优的聚类和特征数量，然后，为每个聚类中心和特征选择设计了一种临界值机制，代理通过相应的临界值可以对聚类中心和特征进行编码，最后通过引力搜索的迭代过程，不断评估代理的适应度，最终得到最优的聚类和特征选择。

3.1 基于引力搜索的数据聚类与特征选择算法GSA_CFS

GSA_CFS算法步骤如下：

步骤1 初始化算法参数，包括代理(种群)数量、最大聚类数量Kmax(由式(12)计算)以及最大迭代次数；

步骤2 生成每个代理，使其包括Kmax个聚类中心数、Kmax+D个主动临界值，其中，D代表每个数据点的维度(见3.1.1节)。初始时，聚类中心和主动临界值随机产生。

步骤3 重复以下步骤，直到满足终止条件：

(1)通过评估选择临界值(见3.1.4节)，寻找每个代理的主动聚类中心和特征；

(2)对于每个数据点，计算其与代理i的每个主动聚类中心的欧氏距离；

(3)分配数据点至距离最小的聚类中；

(4)如果没有数据点分配至一个聚类中，则通过3.1.5节中的方法重新计算聚类中心；

(5)利用GSA算法修改代理，通过代理的适应度值指导代理搜索过程；

(6)分配选择临界值至每个聚类及聚类中的每个特征，选择临界值基于修改的代理进行计算，见3.1.2节；

(7)基于部署(3)～(6)计算的选择临界值计算聚类中心和特征的截止临界值；

步骤4 在最后一次迭代中，最优代理将提供最优的特征子集和聚类中心以及聚类数量。

3.1.1 代理表示及初始化

算法利用一种变量合成代理表示策略对拥有不同聚类数量的特征和聚类中心进行编码。算法中，对于N个数据点，一个代理由维度为(Kmax+D)+(Kmax×D)的实数矢量组成，每个数据点拥有D个维度，最大聚类数量为Kmax。此时，聚类数量的上限值为Kmax，等于给定数据集中数据点的数量的开方

(12)

第一部分(Kmax+D)由两个记录Kmax和D组成，所分配的值为[0,1]间的正实数值。第一个记录Kmax的值用于对聚类过程中对应的聚类是否被激活进行决策，第二个记录D的值表明是否对应的特征被激活。第二部分(Kmax×D)表示维度D中每个维度上的Kmax个聚类中心。在特定时间t时代理i的矢量表示为图1所示，此时，i代表种群规模，i=1,2,…,P。

图1 代理编码表示

其中，mcij为代理i的第j个聚类中心，TCij为聚类中心mcij对应的临界值，TFij为代理i的每个聚类中第j个特征的临界值，TCij和TFij分别表示选择活跃聚类中心和特征时的选择临界值。以下以一个实例对其说明：

实例1：令Kmax=4，D=3，即最大聚类数量为4，空间为3维。代理编码如图2所示。

图2 实例1

矢量中的前4个记录(0.6,0.7,0.4,0.3)代表对应4个聚类的聚类选择临界值，后面的3个记录(0.7,0.3,0.8)表示特征选择临界值(由于每个聚类拥有3个特征)。剩余的记录表示4个聚类中心，即(4.9,3.2,1.6)、(5.7,4.4,1.0)、(6.9,3.0,4.9)和(7.7,3.1,2.4)。

3.1.2 临界值计算

聚类数量本质上对应于给定数据集的变化。因此，对于聚类中心的选择临界值定义为

(13)

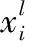
对应于每个聚类的相同特征与所有聚类间的关联通过以下公式计算

(14)

式中：TFq表示数据集中第q个特征的临界值，Vrq表示数据集中第q个特征的方差，Vrq,i表示第i个聚类中特征q的方差，K代表数据集的聚类数量。

TFq描述聚类结构中特征q的重要性均值，该值接近于1，表明当前解中的所有聚类在该特征下相互远离，使其可用于决定聚类结构。

3.1.3 截止临界值计算

聚类选择的截止临界值定义为

(15)

类似地，特征选择的截止临界值定义为

(16)

算法开始时，截止临界值Tcutoff_center和Tcutoff_feature均设置为0.5。

实例2：实例1中代理的聚类中心和特征选择分别为(0.6,0.7,0.4,0.3)和(0.7,0.3,0.8)，基于以上截止临界值概念，Tcutoff_center和Tcutoff_feature分别为0.5和0.6。

3.1.4 活跃聚类中心及特征提取

代理中的聚类中心和特征选择是基于相应的截止临界值的，即Tcutoff_center和Tcutoff_feature。若聚类中心的临界值TCij大于Tcutoff_center，则相应的聚类中心mij被选择分割数据集合；否则，不被选择。活跃聚类中心提取规则如下：

若TCij>Tcutoff_center，则代理i的聚类中心j是活跃的，即mij是活跃的，否则，聚类中心j不活跃；此时，TCij代表代理i的第j个聚类中心，Tcutoff_center为聚类中心的截止临界值。

类似地，活跃特征提取规则如下：

若TFij>Tcutoff_feature，则代理i的每个聚类中心的特征j是活跃的，否则，特征j不活跃。此时，TFij代表代理i的第j个特征，Tcutoff_feature为特征的截止临界值。

若在GSA算法执行过程中，不存在任一临界值大于截止临界值，则随机选择两个临界值并初始化至大于截止临界值。

实例3：实例1中代理的聚类中心和特征选择临界值分别为(0.6,0.7,0.4,0.3)和(0.7,0.3,0.8)，实例2中的聚类中心截止临界值Tcutoff_center和特征截止临界值Tcutoff_feature分别为0.5和0.6。首先，聚类中心临界值用于选择给定数据集的聚类数量，根据以上提出的规则，仅有两个聚类中心的临界值(0.6和0.7)大于0.5，且对应的活跃聚类中心为(4.9,3.2,1.6)和(5.7,4.4,1.0)。活跃聚类中心圆形区域部分，如图3所示。然后，特征选择临界值用于从对应的活跃聚类中选择重要的特征形式，此时，两个特征选择的临界值(0.7和0.8)大于截止临界值0.6，则在每个活跃聚类中心中的第一个和第三个特征被选择，即粗体部分。

图3 实例3

3.1.5 聚类中心确认

有可能一个特定聚类不存在任一数据点，即可能出现空聚类。在一个聚类中心超过分布点的边界时会出现这种情况。该问题可以通过重新对特定代理的聚类中心进行重新初始化解决。现在分配n/K个数据点至每个聚类中心，使得每个数据点被分配至离其最近的特定聚类中。

实例4：考虑三维特征空间中拥有150个数据点的数据集，活跃聚类数量为3。假设一个特定代理的聚类中心为((1.9,0.52,-0.02),(5.0,4.1,0.9),(7.1,2.2,1.8))。没有任一数据点分配至聚类中心(1.9,0.52,-0.02)，由于该中心处于数据点分布的边界以外。基于以上提到的平均计算公式n/K，即30个数据点被分配至最近的聚类中心。因此，最新形成的聚类中心为(4.128,3.269,1.601),(3.900,2.832,1.266)和(5.789,3.456,0.976)。

3.1.6 适应度计算

聚类算法的性能取决于聚类标准。本文选择I-index指标对聚类算法性能做出评估，定义为

(17)

(18)

(19)

其中，K为分割数据集所选的聚类数量，P值取2。I-index取值越高，聚类解的质量越好。

本文研究了与聚类和特定数量相关的两个优化问题，并将其合并至I-index中。

问题1：寻找最优的聚类数量。本文通过考虑Kmax的影响，设计了以下惩罚函数

Penality1=Kmax-K

(20)

该惩罚函数偏好更少的聚类数量，它与(Kmax-K)成比例。

问题2：寻找最优的特征数量。多数的聚类指标没有考虑合适的特征数量。特征选择即从所有特征量中选择d个特征D。保留重要特征有助于确保聚类性能，为了降低特征数量对性能的影响，引入另一惩罚函数

(21)

结合以上定义，聚类评估指标可定义为

fitness=I(K)×Penality1×Penality2

(22)

(23)

3.2 复杂度分析

(1)算法的初始化时间复杂度为O(agentsize×stringlength)，agentsize为代理数量，stringlength为每个编码代理的长度，而stringlength则为O((Kmax+D)+(Kmax×D))，D为数据集的维度，Kmax为最大聚类数量。

(2)算法的活跃聚类和特征提取时间复杂度为O(agentsize×Kmax×D)。

(3)适应度计算包括3步：数据点至不同聚类的分配对于每个代理的时间为O(n2×Kmax)，聚类中心更新时间为O(Kmax)，适应度计算的时间为O(n×Kmax)。算法的步骤3需要在所有代理上递归，即3个子步骤乘以agentsize次。因此，步骤3的总体时间要求(计算适应度)为agentsize×(n2×Kmax+Kmax+n×Kmax)=O(agentsize×n2×Kmax)。

(4)算法的代理质量计算时间为O(agentsize×stringlength)。

(5)算法的加速度计算时间为O(agentsize×stringlength)。

(6)算法的代理速度和位置更新计算时间为O(agentsize×stringlength)。

综上，若stringlength远小于n，则每次迭代的时间复杂度为O(agentsize×n2×Kmax)，算法的总体时间复杂度则为O(agentsize×n2×Kmax×Maxgen)，Maxgen即为最大代数。

4 仿真实验

4.1 环境搭建

GSA_CFS算法的运行与多个不同的控制参数相关，包括：代理数量P、最大迭代次数Maxgen和引力常量G0。实验中设置P=30，Maxgen=100，G0=100。参数固定后，算法运行20次并取结果的平均值进行性能评估。引用UCI数据库中8种实际的测试数据集对算法性能进行仿真测试，所选取的测试数据集涵盖了低、中和高维度的数据实例，表1描述了所选的8种经典数据集的特征，然后同其它数据聚类算法进行仿真测试。

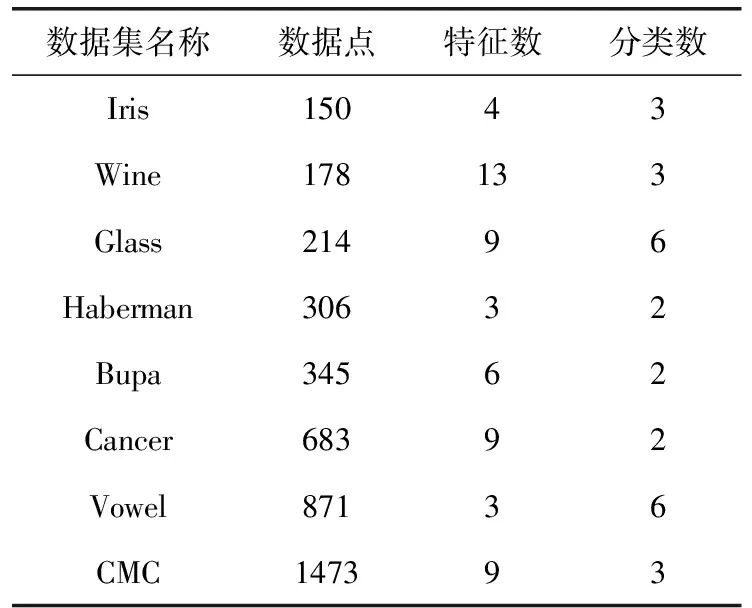
表1 测试数据集相关描述

4.2 特征选择的相关性

所选特征的价值可以通过特征选择的频率和调和分值LS确定。特征选择的频率定义为

(24)

式中：分子表示特定特征在算法运行中被选择的次数，分母表示算法实施聚类独立运行的次数。表2是GAS_CFS算法得到的不同数据集中特征选择的频率和LS情况。可以看到，对于Iris数据集，GAS_CFS算法非常频繁地选择了特征量3和4，该特征也拥有较高的LS值。对于Wine数据集，GAS_CFS算法频繁选择了特征量1、6、7和13。类似地，对于Glass，1、3、4、7是最频繁的特征选择。对于Haberman，最频繁的特征选择是1和3。其它数据集的特征量选择结果也可以依次看出。

表2 特征选择频率及其LS值

4.3 聚类选择的相关性

为了区分不同聚类的重要性，需要计算所选聚类数量的频率及其对应的聚类准确率Ac。聚类频率计算为

(25)

式中：分子表示特定聚类在算法运行中被选择的次数，分母表示算法实施聚类独立运行的次数。表3是GAS_CFS算法得到的不同数据集中聚类选择的频率及其聚类准确率Ac的情况。对于Iris数据集，算法生成了3个聚类，对应的聚类准确率较高。对于Wine，算法也生成了3个聚类。对于Glass，生成聚类数量较为频繁的是5和6个。对于Haberman则最为频繁的聚类数是2。其它数据集的聚类量选择结果及聚类准确率也可以依次看出。

表3 聚类选择频率及聚类准确率

4.4 同类型算法的性能对比

选择7种典型的数据聚类算法进行性能对比，包括：K均值算法K-means[7]、改进的和声搜索聚类算法MHSC[8]、基于蚁群优化的特征选择与聚类算法FS_ACO[9]、基于粒子群优化的特征选择与聚类算法CFS_PSO[10]、基于文化基因算法的聚类算法NMA_CFS[11]、自冶和声搜索聚类算法HS_CFS[12]以及改进文化基因聚类算法INMA_CFS[13]。算法的最大迭代次数和种群规模分别设置为500和30，每个数据集按序运行20次，聚类质量的度量根据平均值和标准方差进行衡量，以展示算法的鲁棒性。表4是相关对比算法的主要参数设置。

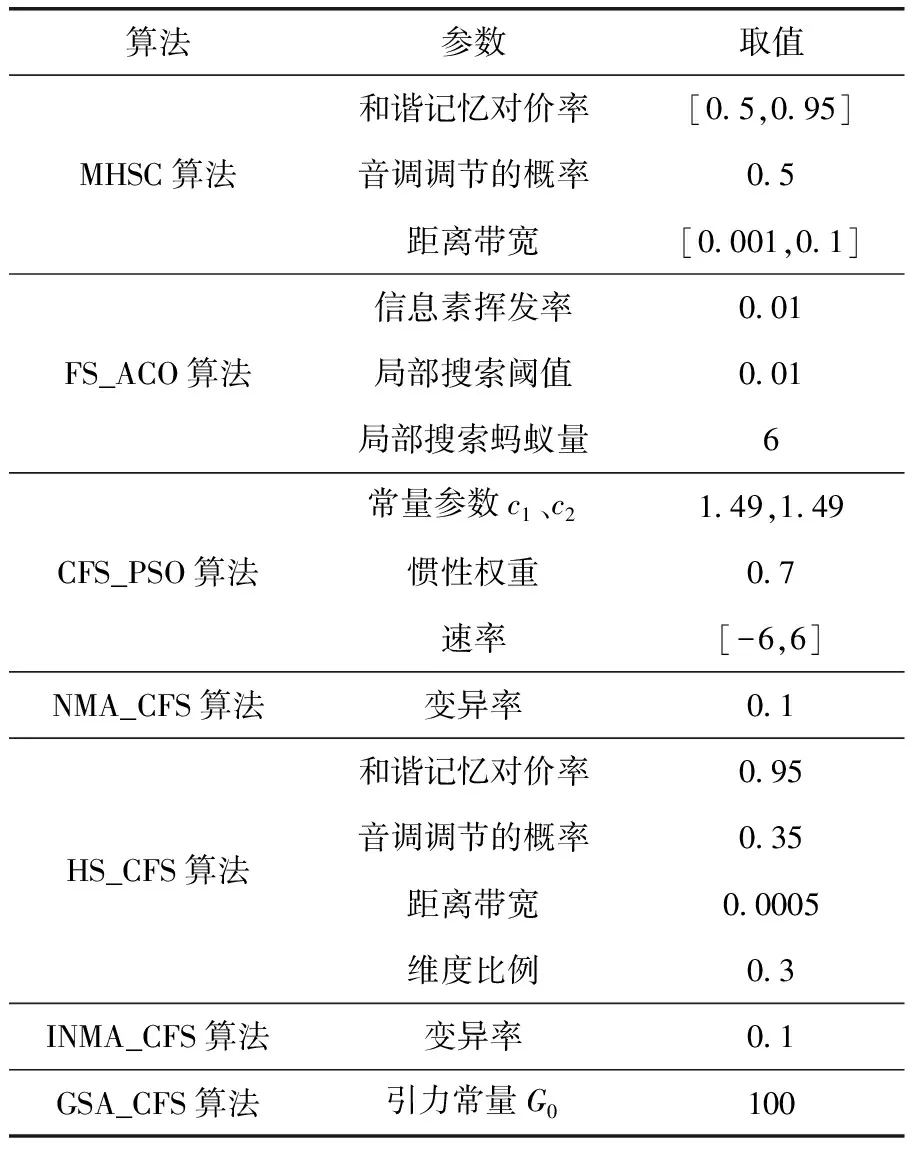
表4 对比算法的相关参数设置

表5给出所有测试数据集中算法得到的聚类数量、特征数量及聚类准确率的均值结果。

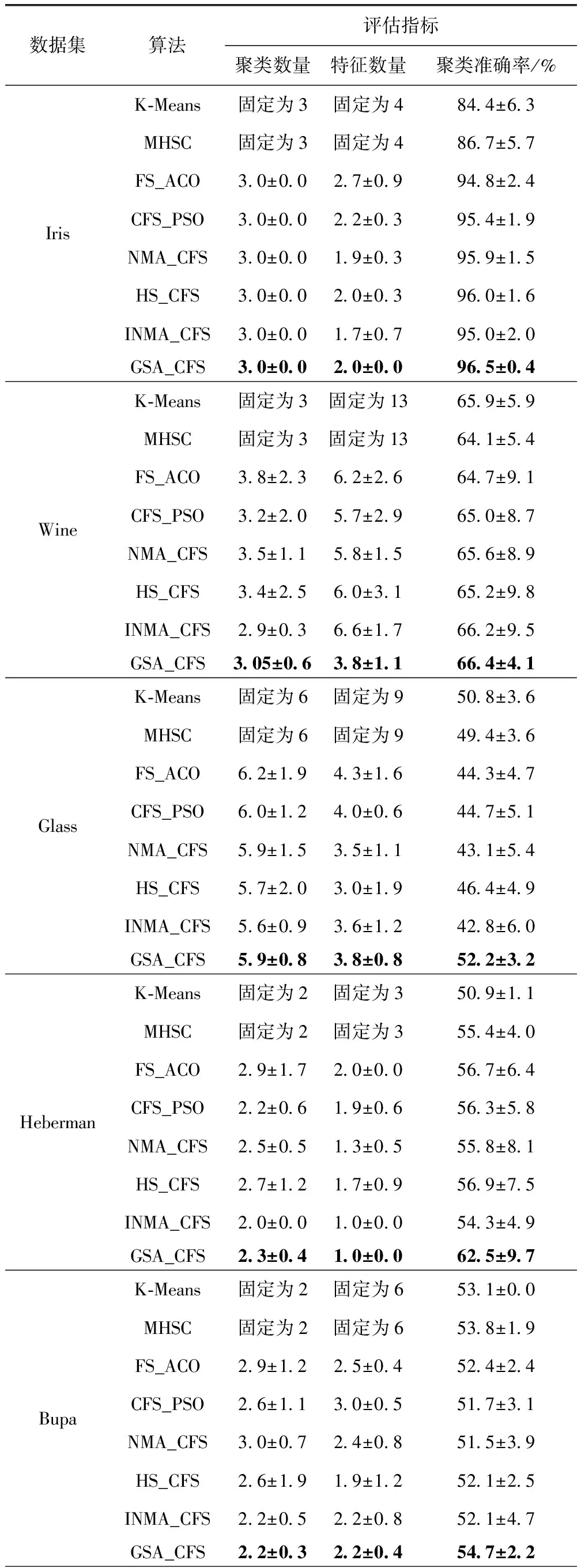
表5 性能比较结果

对于Iris，GSA_CFS拥有最优的聚类准确率，然后依次是HS_CFS、NMA_CFS、CFS_PSO、INMA_CFS、FS_ACO、MHSC、K-Means。GSA_CFS、INMA_CFS、NMA_CFS、CFS_PSO、FS_ACO和HS_CFS都可以正确聚类数量和特征，而本文算法则在每次运行过程均选择了特征量3和4。

对于Wine，GSA_CFS获得了比其它算法更高的聚类准确率，其聚类数量为3，NMA_CFS、CFS_PSO、FS_ACO和HS_CFS选择的特征数量为6，而INMA_CFS生成了7个特征，而本文算法找到的最佳特征量为4。

对于Glass数据集，所有聚类算法产生的聚类数量均为6，INMA_CFS、NMA_CFS、CFS_PSO、FS_ACO和GSA_CFS得到的特征数量均为4。然而，HS_CFS的特征数量为3，本文算法则比其它算法提供了改进效果更好的聚类准确率。

对于Haberman数据集，本文算法的聚类准确率为62.5%，HS_CFS和NMA_CFS分别为56.9%和55.8%。FS_ACO、CFS_PSO和HS_CFS生成的特征数量为2。INMA_CFS、NMA_CFS与本文算法在聚类和特征数量上得到相似的结果。

对于Bupa数据集，GSA_CFS算法得到的聚类量和特征量均为2，而NMA_CFS、FS_ACO、CFS_PSO和HS_CFS提供了不同准确的聚类量。HS_CFS得到的特征量为2。显然，本文算法在聚类和特征量的聚类准确率要高于其它算法。

对于Cancer数据集，所有算法均得到了准确的聚类和特征，但聚类准确率上本文算法是高于其它算法的。对于Vowel和CMC数据集，GSA_CFS得到了最佳的聚类准确率，其它依次是HS_CFS、FS_ACO、CFS_PSO、NMA_CFS、INMA_CFS、MHSC以及K-Means算法。

5 结束语

设计了一种基于引力搜索机制的数据聚类与特征选择算法。首先，提出一种变量合成代理表示策略使得算法可以同步寻找最优的聚类和特征数量，然后，为每个聚类中心和特征选择设计了一种临界值机制，代理通过相应的临界值可以对聚类中心和特征进行编码，最后通过引力搜索的迭代过程，不断评估代理的适应度，最终得到最优的聚类和特征选择。