数值堆热工流体程序CVR-PACA验证及典型应用

王明军，鞠浩然，赵民富，李伟卿，刘天才，胡长军，杨 文，田文喜，秋穗正，苏光辉

(1.西安交通大学 核科学与技术学院，陕西 西安 710049；2.中国原子能科学研究院 反应堆工程技术研究所，北京 102413；3.北京科技大学 计算机与通信工程学院，北京 100083)

数值堆技术是当前核能领域的新兴技术，是各核能大国相互争夺的核科技战略高地之一。数值堆技术基于高精度数值仿真技术、大数据应用技术和高速数据传输技术，应用先进的反应堆物理、热工水力、安全分析、燃料性能、材料性能、结构力学、耦合接口等计算软件，面向某一反应堆实体系统进行全方位、全周期的数字化模拟，并采用可视化及人机交互技术直观展示模拟预测结果，完成反应堆内各物理场现象的研究，是未来核能系统的先进研究平台。当前时期，美国、欧盟均提出了各自的数值堆技术路线，并大力发展相应的关键技术：欧洲主要完成了以SALOME开源软件平台为基础的反应堆多物理场耦合模拟技术，拓展了平台集成、模型开发、耦合技术、不确定性分析及验证等方法，对轻水堆安全分析、运行和工程设计给出综合性解决方案；美国能源部则通过启动NEAMS计划，用于部署和发展先进核能技术，计划支持开发的多种高精度计算分析程序发展迅速，并已在各相关科研领域产生了一定的影响。此外，日本、韩国等核能强国也积极参与到数值堆相关技术的研究工作中。

为实现由核能大国向核能强国的跨越，我国紧跟国际核能科技发展前沿，投入了大量资源进行数值堆相关的专业软件研发和应用工作。其中，依托国家重点研发计划项目“数值反应堆原型系统开发及示范应用”的资助，开发了中国数值反应堆原型系统CVR1.0[1]，系统主要包含热工、物理、材料、燃料、结构力学5种专业工具及所依托的耦合平台。其中，热工水力分析工具包括高精细CFD计算工具CVR-PACA及堆芯子通道分析工具CVR-PASA。本文详细介绍CVR-PACA程序在反应堆堆芯热工分析方面的典型应用情况——各类棒束通道内湍流流场的分析建模方法、预测结果分析及模型验证等应用，验证依托高精度谱元方法的大涡模拟(LES)模型及非稳态雷诺时均(URANS)模型的适用性，多角度展示CVR-PACA在数值堆精细化热工分析方面的多场景应用能力和计算精度，定量证明该程序具有出任CVR1.0系统热工计算模块重要组成部分的能力。

1 数值方法及湍流模型简介

1.1 谱元方法

谱元方法是一种高精度偏微分方程离散数值方法，是谱方法和有限元方法的融合。谱元法采用高斯多项式函数插值的方式获得谱元内部的场参数的精细分布，能够极大降低截断误差，提高计算精度。CVR-PACA采用勒让德正交多项式作为插值多项式基底：

(1)

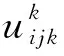
(D(u(x,y,z)|Ωk),ν)=(f,ν)

(2)

式中：D(u)=f为所求解的偏微分方程；(·,·)为内积算符；ν为试函数空间。当采用伽辽金方法时，由于试函数空间ν及基函数空间为同一正交函数空间，因而要求计算网格必须为全六面体网格，以保障函数空间的正交性。这一要求为空间离散网格划分过程提出了较大挑战。

1.2 时间分裂法求解N-S方程

不可压缩流动N-S方程的一般形式为：

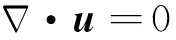
(3)

为叙述方便，将动量方程简化为以下形式：

(4)

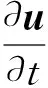
非稳态项应用k阶向后差分格式离散：

L(un+1)+fn+1

(5)

式中，bj为k阶向后差分格式各离散项前系数。

非线性项N(u)采用显式外推格式：

(6)

式中，aj为显式外推格式各离散项前系数。

线性项L(u)进行以下变形：

(7)

式中：μ为流体动力黏度；I为单位矩阵。

外力源项f采用显式计算方法，式(4)可整理为：

(8)

式中：F(un)为本时刻已知项；除外力源项f外，上标n+1为本时刻待求项；上标小于等于n为已知项。式(8)可采用时间分裂法分3步完成求解：

(9)

(10)

(11)

式(9)为非线性步，用于求解时间相关项。式(10)为压力步，通过变形获得以下压力泊松方程，利用谱元方法数值求解压力对流场的作用：

(12)

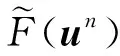
(13)

采用谱元方法结合速度边界条件即可求得当前步速度分布，进而完成时间分裂法求解瞬态N-S方程的步进计算过程。

1.3 湍流模型

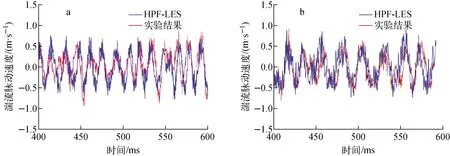
目前，CVR-PACA能够支持高通滤波大涡模拟(HPF-LES)模型及URANS SSTk-ω模型。其中HPF-LES模型在文献[2]中有较为详细的介绍。滤波后的无量纲化N-S方程形式为:

(14)

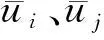
(15)

URANS模型方面选择SSTk-ω模型用于计算验证，该模型已广泛应用于搅混翼棒束通道流场预测[6-9]，并获得了较高的认可度。文献[10]中详细说明了相关模型的实现过程。

2 典型应用算例

2.1 单棒光棒通道

为验证HPF-LES模型对棒间湍流搅混现象的预测能力，本文对韩国SOFEL实验段的单根光棒稠密栅元进行建模[11]，预测流道中的湍流流动搅混特性。为使计算建模区域长度包含4个完整的子通道间湍流脉动拟序结构，保障计算结果的正确性[12]，研究将建模区域长度设为40Dh，Dh为流道的水力直径。轴向设置周期性边界使计算区域封闭。计算预测的速度场分布如图1所示。可以看到当流场达到充分发展流态时，相邻子通道间的窄缝处存在较为明显的横向脉动现象。

a——猝发过程；b——充分发展流态图1 猝发及充分发展时的湍流无量纲速度场Fig.1 Turbulent dimensionless velocity field during burst and fully developed condition

算例对节径比P/D=1.03、1.06，雷诺数Re=20 500条件下的湍流脉动现象进行了定量分析，并与实验结果进行对比，结果如图2所示。可以直观看到，HPF-LES模型能准确预测湍流脉动流场细节，获取各脉动峰，脉动频率计算方面也符合较好。为实现对湍流脉动现象的进一步分析，采用湍流脉动系数β定量评估子通道间的湍流搅混能力：

a——节径比1.03，Re=20 500；b——节径比1.06，Re=20 500图2 子通道间窄缝中心处的横向湍流脉动速度瞬时值Fig.2 Transverse transient velocity at center of narrow gap between adjacent sub-channels

(16)

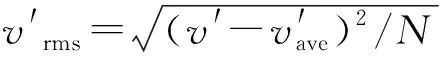
研究整理了P/D=1.06条件下β随Re的变化，并与理论推导值和实验测量值进行对比，结果如图3所示。可以看到，该结果定量验证了HPF-LES模型在预测单棒通道内湍流流场方面的精确程度，仿真计算结果与实验值及理论推导规律符合良好，采用相同的模型参数可外推至其他相似几何条件用于准确预测相关湍流脉动现象。

图3 湍流脉动系数与Re的关系Fig.3 Relationship between turbulent mixing coefficient and Reynolds number

2.2 3×3稠密栅元光棒棒束通道

为进一步分析稠密栅元光棒棒束通道内更细致的湍流搅混现象，研究利用3×3棒束通道对不同类型子通道间的搅混现象进行定量分析。计算所采用的网格生成策略与2.1节相似：近壁面第1层网格高度严格满足y+<1，轴向长度为40Dh，流动出入口设为周期性边界。P/D=1.06、Re=15 000时计算获得的湍流流场瞬时值如图4所示。

1——中心通道间脉动速度提取点；2——边通道间脉动速度提取点；3——边通道与中心通道间脉动速度提取点；4——角通道与边通道间脉动速度提取点图4 3×3光棒棒束子通道内的无量纲速度场分布Fig.4 Dimensionless velocity field distribution in sub-channel of 3×3 bare rod bundle

由图4中纵截面可看出，不同子通道间的湍流脉动速度大小差异较为明显。为定性研究该现象，选取图4中标出的4处窄缝中心位置提取横向瞬时速度，用于定量对比。图5示出P/D=1.06时不同Re条件下不同位置湍流脉动速度瞬时值的对比。对比同一子图各曲线可知，湍流脉动速度的幅值和频率受Re影响显著，可采用监测脉动速度的方式初步判断流体流动的状态(层流、转捩、充分发展湍流流态)；对比不同子图中的相同Re条件下的曲线可知，湍流脉动速度幅值和频率受监测点两侧子通道几何形状影响显著。在中心通道间的湍流脉动现象最为显著，临近角通道相连窄缝处的脉动搅混能力最弱。

a——点1处；b——点2处；c——点3处；d——点4处图5 各监测点的脉动速度瞬时值Fig.5 Transient turbulent mixing velocity at different monitoring points

研究采用快速傅里叶变换(FFT)方法对上述脉动速度进行了频域分析，获得了相应的脉动峰值特征频率，P/D=1.06、Re=20 500时的结果如图6所示。由图6可见：脉动峰值受几何位置影响显著，监测点距离角通道越近，脉动峰值越低。原因在于，相比于中心通道内的流体涡旋，边角通道内的涡旋受几何限制更为显著，通道较为局促，流动摩擦阻力较大，涡旋含能较低，涡旋旋转频率减弱。但由于几何形状难以采用准确的数学参数予以反映，因而目前可直接采用修正系数的方法反映几何形状对脉动频率的影响。

a——点1处；b——点2处；c——点3处；d——点4处图6 各监测点脉动特征频率Fig.6 Characteristic frequency at different monitoring points

对于湍流脉动引起的子通道间搅混效应，同样采用无量纲量湍流脉动系数β进行定量分析，P/D=1.06时的仿真预测结果列于表1。由表1可见，几何条件对湍流搅混效应同样具有较为显著的影响，角通道间隙处的搅混系数较中心通道处降低25%左右。因此，在采用计算获得的湍流搅混系数指导子通道程序计算子通道间横向搅混计算时，与脉动频率类似，可适当引入修正系数，提高其建模精度；或可直接采用角通道临近位置所获得的脉动系数结果进行计算，以保证计算过程的保守性。

表1 湍流脉动系数随不同监测点和Re的分布Table 1 Turbulent mixing coefficient distribution case at different monitoring points and Re

2.3 带搅混翼棒束通道

为验证CVR-PACA在预测搅混翼下游湍流流场的精确程度，本文应用该程序对搅混翼棒束通道基准题Matis-H进行了建模计算[13]。几何建模方面，计算域选取了中心3×3棒束所围成的2×2子通道作为建模对象；周向采用4对周期性边界用于计算域的封闭。速度入口边界设定方面，本次计算测试了简易速度边界设置方案对计算结果的影响。简易速度边界的具体设置方案如下：1) 定位格架上游光棒长度不进行加长处理，入口段光棒长度仅设置为1Dh；2) 速度入口面上的速度分布采用层流流动的速度分布，具体为：

(17)

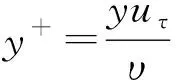
网格划分方面，研究采用网格分区划分结合网格分裂的方法建立复杂结构的全六面体网格。分区方案如图7a所示。为满足大涡模拟湍流模型计算要求，在生成边界层网格时，需严格满足近壁面第1层网格高度y+<1的条件。最终建立的六面体网格的部分结果如图7b、c所示。

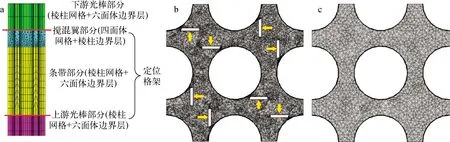
a——网格划分策略；b——定位格架条带部分网格；c——定位格架下游光棒部分网格图7 3×3棒束六面体计算网格Fig.7 Hex mesh of 3×3 rod bundle

不同模型搅混翼下游不同位置处时均速度场及脉动速度场计算结果与实验值的对比如图8、9所示。由图8，图9a、b可看到，在时均场预测方面，HPF-LES模型及URANS SSTk-ω模型均与实验值较为接近，均能较好地预测撕裂式搅混翼下游的时均速度分布；然而，脉动场方面，由图9c、d看到，URANS模型的预测能力明显不足，HPF-LES模型准确预测了脉动速度分布的峰值位置，在脉动场预测方面具备一定能力。

为验证简易速度边界设置方法配合HPF-LES模型的联合计算方案对搅混翼下游流场的预测能力，将该方案计算结果与基准题sp05算例[13]的计算结果进行了定量对比。sp05算例与本研究采用相同的几何建模方案，不同点在于sp05算例采用RSM-SSG RANS模型完成计算，入口段采用延长光棒长度的方式制造充分发展湍流流态支撑计算。图9示出本文研究与sp05算例的流场对比，可以看处，HPF-LES模型在时均速度场预测方面更为准确，脉动速度场预测方面，HPF-LES模型同样能够更好地捕捉相关细节，预测相关峰值，因而HPF-LES模型配合简易速度边界设置的联合计算方案具有一定可行性。

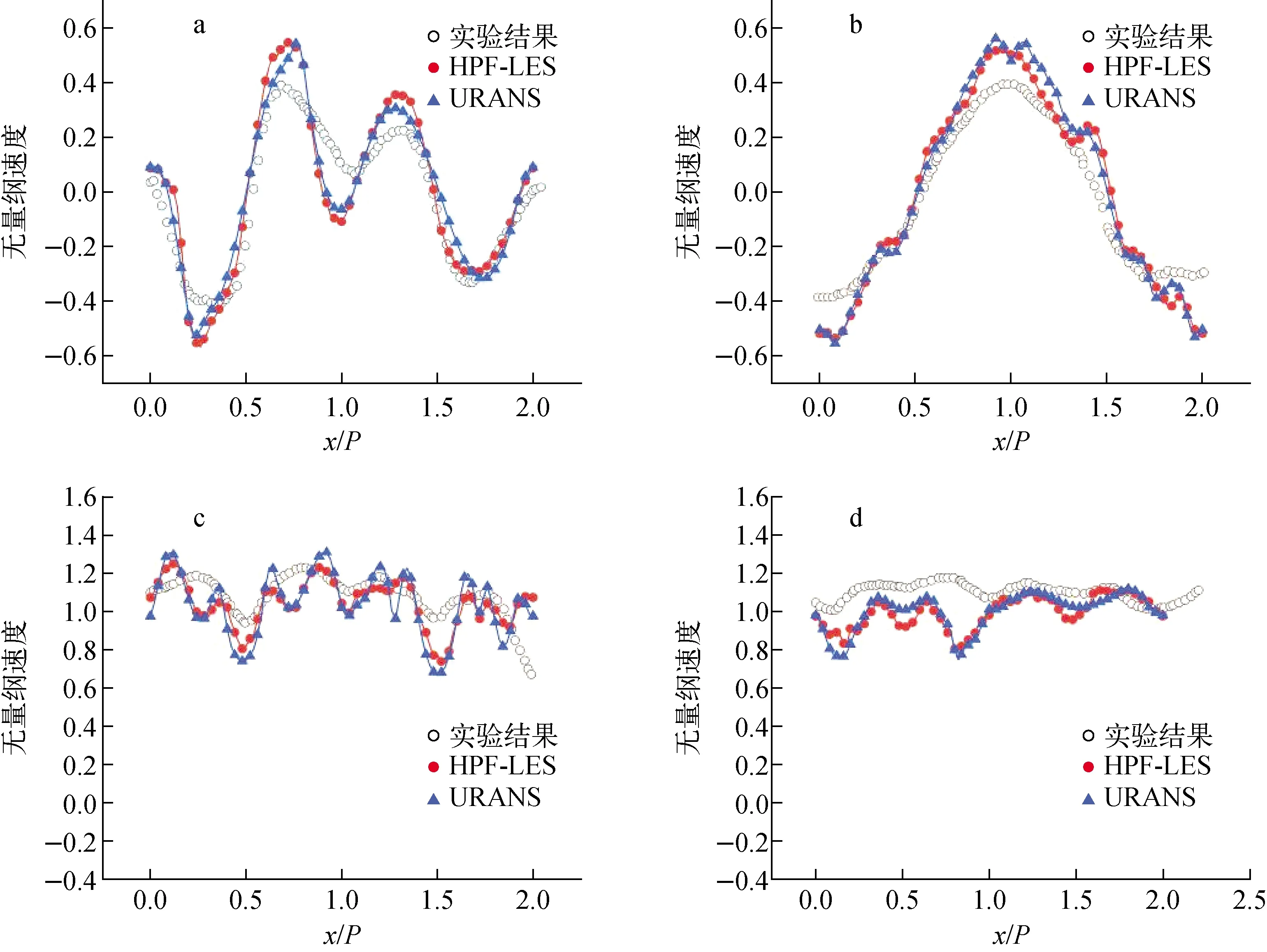
a——搅混翼下游0.5Dh处y方向速度分量；b——搅混翼下游1.0Dh处x方向速度分量；c——搅混翼下游1.0Dh处z方向速度分量；d——搅混翼下游4.0Dh处z方向速度分量图8 时均速度场综合对比Fig.8 Comprehensive comparison of time-averaged velocity

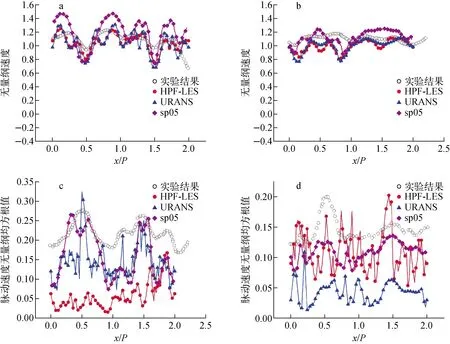
a——搅混翼下游1.0Dh处时均速度z分量；b——搅混翼下游4.0Dh处时均速度z分量；c——搅混翼下游1.0Dh处脉动速度z分量；d——搅混翼下游4.0Dh处脉动速度z分量图9 不同入口处理方案下搅混翼下游流场的对比Fig.9 Comparison of downstream flow field of mixing vane under different inlet treatment schemes

为进一步探究HPF-LES模型与简易入口设置方案匹配的具体原因，截取了定位格架处的速度剖面进行研究，如图10所示。由图10可知：采用HPF-LES模型计算时，定位格架的下沿作为产生的前台阶几何形状能够猝发湍流流态的形成，从而快速促进湍流流态的发展；同时，湍流在流经定位格架条带结构时，湍流流态迅速发展，流经搅混翼附近时已转化为充分发展状态；对比而言，由于URANS模型很大程度上均匀化了流场细节，难以利用条带结构促进湍流涡的形成，因而不能很好地猝发湍流流型，获得的脉动细节也不够充分。

a——HPF-LES模型；b——URANS SST k-ω 模型图10 HPF-LES模型及URANS模型的瞬时无量纲速度分布Fig.10 Transient dimensionless velocity distribution calculated by HPF-LES model and URANS model

图11示出采用HPF-LES模型及URANS模型计算得到的搅混翼下游湍动能云图及横向速度矢量分布的预测结果，可以看到，HPF-LES模型预测结果显示出了湍动能的分布规律：在与轴向垂直的横截面上，湍动能一般集中分布在存在大型涡旋的子通道中央，同时可观察到湍动能随小涡旋在子通道间迁移的特性；轴向上，随着横截面到搅混翼的距离增加，流动的混乱程度减弱，湍动能也逐渐减弱。URANS模型不能很好预测这一分布规律，需采用合理的入口条件支撑计算。

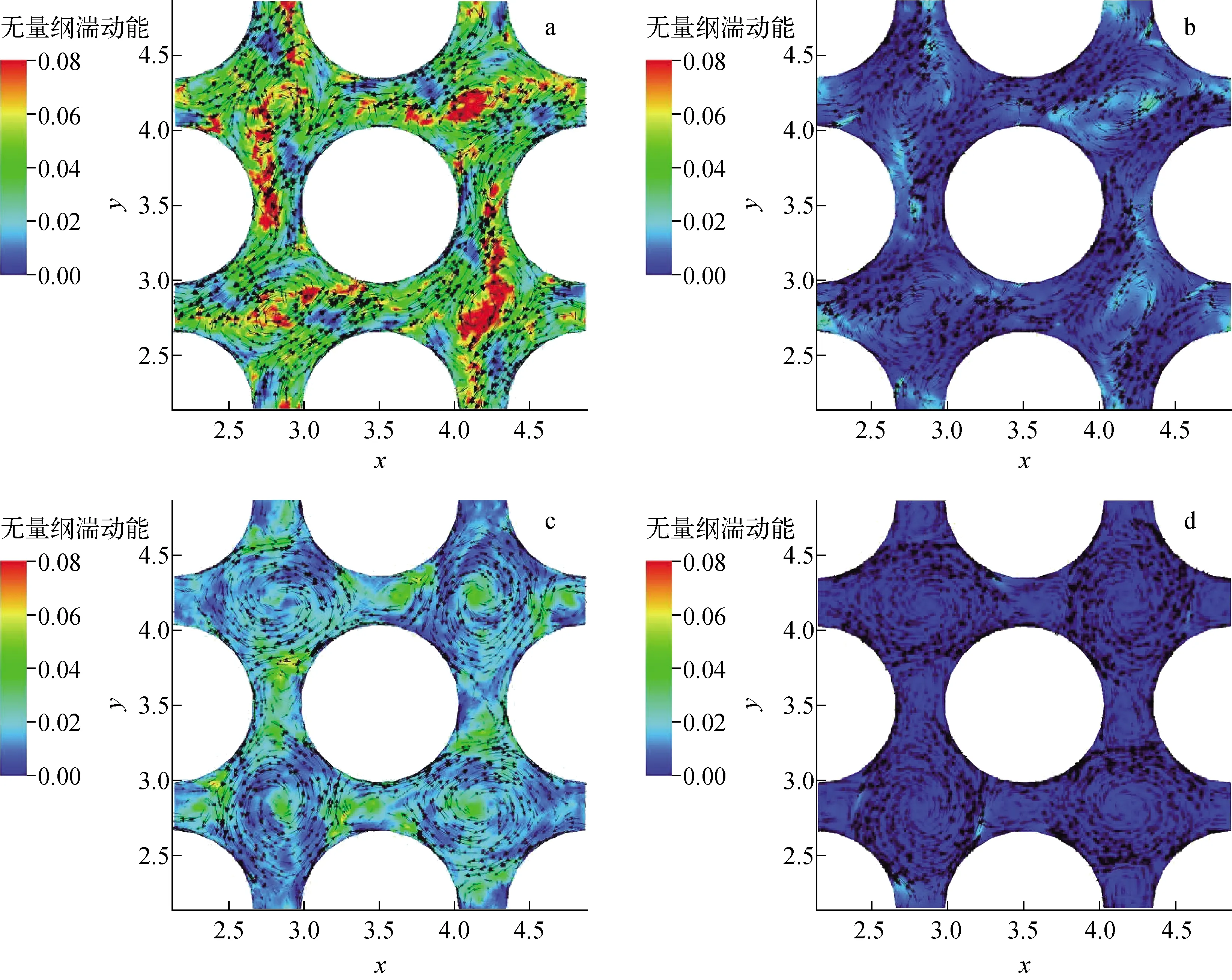
a——HPF-LES模型，0.5Dh；b——URANS模型，0.5Dh；c——HPF-LES模型，4Dh；d——URANS模型，4Dh图11 搅混翼下游不同截面处湍动能及横向时均速度矢量分布Fig.11 Turbulent kinetic energy and time-averaged transverse velocity profiles at different cross sections of mixing vane downstream

2.4 带绕丝棒束通道

研究KALLA-KIT 19棒束组件实验，对带绕丝棒束通道内的热工现象进行了计算分析，以验证建模方案的可行性和精确性。实验采用液态铅铋合金作为工质。绕丝样式采用简化的垂直连接方式，其详细几何参数参见文献[14]。计算采用网格分裂方案实现六面体网格生成，最终的网格划分结果如图12所示。

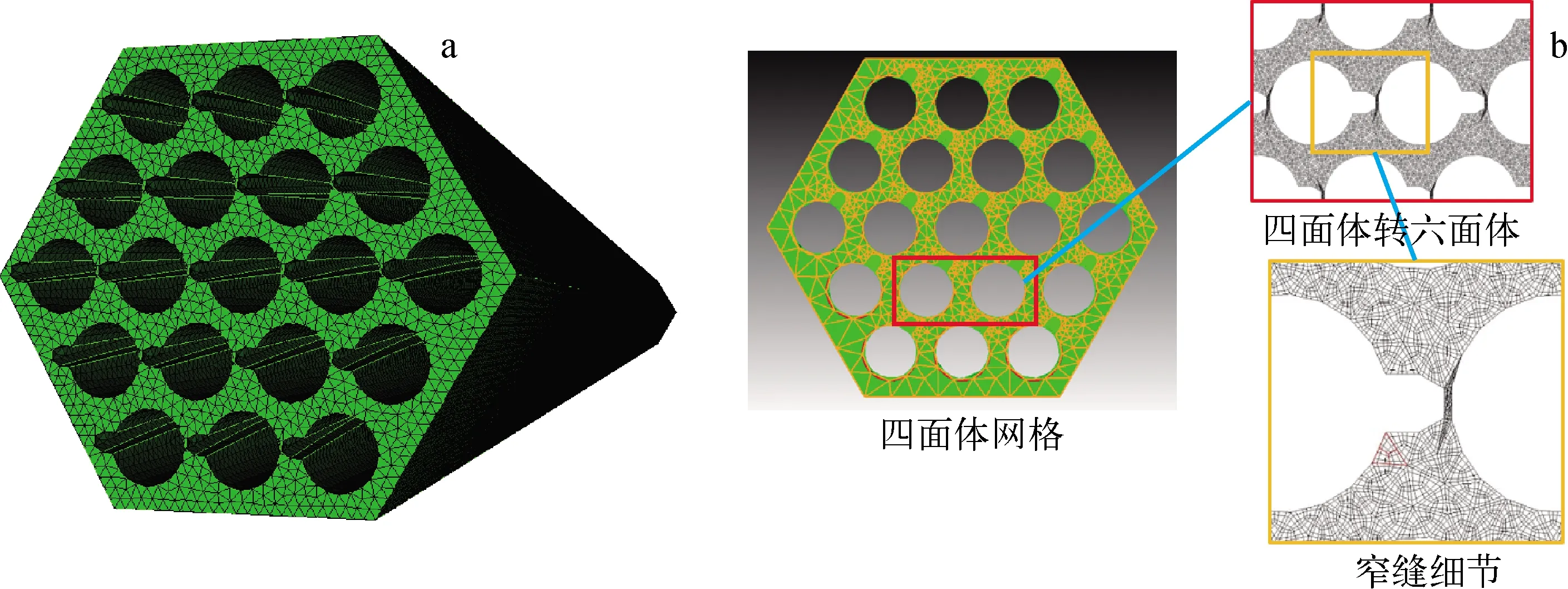
a——四面体网格总览；b——截面网格细节图12 19棒绕丝组件网格示意图Fig.12 Mesh scheme of 19 wire-wrapped rod bundles

计算采用无量纲化N-S方程进行。为还原KALLA-KIT实验采用的定热流密度的加热方案，本文采用固定入口流体温度和壁面热流密度的方式设定边界条件，用于支持能量方程求解。壁面热流密度的无量纲化方面采用下式实现：

(18)

式中：qw为壁面绝对热流密度；ρ流体密度；T0为特征温度；v0为特征速度，本算例设为入口平均速度；q′w为无量纲化壁面热流密度；cp为流体比定压热容。为简化假设，设定热流密度均匀布置于燃料棒与绕丝的表面。

图13、14分布示出19棒绕丝算例的速度与压力瞬时值分布及压力分布的细节。压力细节方面，由于绕丝沿各燃料棒顺时针绕动，相应的导流特性使各截面上的压力峰值区域也沿轴向按顺时针变化；另外由于采用URANS模型计算，一定程度上反映了瞬时流场的流动细节，因而压力场不尽光滑平顺。

图13 19棒绕丝组件的无量纲速度(a)及无量纲压力(b)分布Fig.13 Dimensionless velocity (a) and dimensionless pressure (b) profiles in 19 wire-wrapped rod bundles

压力分布：a——z=40Dh；b——z=80Dh；c——z=120Dh图14 19棒绕丝组件的无量纲压力分布细节Fig.14 Dimensionless pressure distribution detail in 19 wire-wrapped rod bundles

图15示出z=20Dh处的瞬时温度分布与横向速度矢量分布。由图15可见，截面内温度分布受流场影响显著。由于子通道内部存在涡旋，致使通道内部温度分布较为均匀；同时，绕丝的位置变化通过影响速度压力分布，最终对温度分布及峰值点存在影响：由于温度梯度减小，液态金属导热输热能力减弱，致使绕丝与燃料棒焊接位置处的传热性能更为恶化，在绕丝的背离面，由于子通道内压力较低，使得局部流动受阻，背离面焊接处换热恶化，因而出现温度峰值。迎风面由于压力升高，促进局部流体流动，因而导致子通道内温度梯度增大，改善换热，局部温度未达到峰值水平。

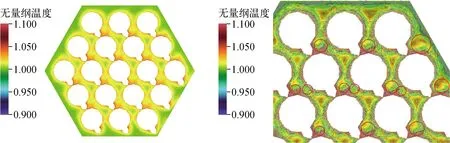
图15 19棒绕丝组件的无量纲温度与横向速度矢量分布Fig.15 Dimensionless temperature and transverse velocity vector profiles in 19 wire-wrapped rod bundles

上述流场流动特性也可由图16直观观察：相邻子通道1和子通道2的流线起始端由红色圈及橘黄色圈标注。其中子通道1为背离面子通道，子通道2为迎风面子通道。可以看到迎风面子通道流体在黄色方框处受绕丝挤压有所偏移，在下游处有部分流体压入子通道2；同时由于子通道2中存在涡旋，对流动有一定的约束作用，使得红色圈内的流线初始呈直线分布(深蓝色流线簇)；随着流体流动，由于红色箭头所指绕丝的背离，形成局部真空，子通道2中的部分流体被吸入该绕丝的背离子通道中，同时由于子通道2中的绕丝旋入子通道1中，对流体产生了挤压，因而在后段部分更多的流体被压入上层子通道中，使得流线分布范围更加宽泛，流体在子通道间的搅混更为复杂充分。

图16 19棒绕丝组件的局部流场流线示意图Fig.16 Scheme of local streamline in 19 wire-wrapped rod bundles

综合分析可知，采用瞬态URANS模型计算能获得绕丝棒束内更多的流动和换热细节，为验证设计的热工特性提供更加丰富的数据，更为精准地指导相关设计的优化改进。

3 结论

本文采用CVR-PACA对单棒光棒通道湍流流场、3×3光棒棒束湍流流场、Matis-H压水堆棒束通道基准题、19棒带绕丝组件通道湍流流场进行了仿真计算，验证了基于高精度谱元数值方法的HPF-LES模型及URANS SSTk-ω模型的适用性和计算精度。模拟过程采用网格分裂技术，结合混合网格生成技术实现了带搅混翼棒束通道、带绕丝棒束通道等复杂几何结构的全六面体网格划分，实现了利用高精度数值方法对各类堆芯组件内流动换热现象预测的典型应用。通过计算分析，可得到以下结论。

1) 对照实验结果，HPF-LES模型能精确计算光棒稠密栅元棒束通道内的湍流流场，精细预测子通道间的湍流搅混现象。该现象受Re及几何条件影响显著，计算获得的相关结论可用于子通道程序的精细化模型开发及修正。

2) 配合高精细划分的全六面体网格，HPF-LES模型及URANS模型均可较好地预测带有搅混翼的定位格架棒束通道下游的时均流场。对于湍流脉动流场，HPF-LES模型受入口段影响较小，可以准确预测脉动速度峰值，但URANS模型受入口段流态影响显著，因此采用具有充分发展湍流流态的入口对于URANS模型计算极为重要。

3) 研究实现了绕丝棒束的全六面体网格的生成策略，采用URANS模型预测了绕丝几何条件下的流动换热现象，基于高精度CFD方案的URANS模型能获得子通道内的精细化压力分布和子通道内的旋涡分布情况，获得的流场结果与温度场分布规律契合较好。通过观察流线能够更为直观地了解绕丝棒束通道内的搅混特性。

通过上述分析方法能够获得更精确的流动和换热细节，为验证设计的热工特性提供更加丰富的数据支撑，为方案优化改进提供定量反馈。