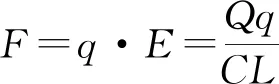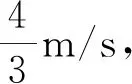图像法解一类“子弹打木块”模型
2021-09-16陈卫国
陈卫国
(北京师范大学贵阳附属中学,贵州 贵阳 550023)
高中物理中有一类常见的“子弹打木块”问题,用常规物理解法计算量很大,且容易出错.笔者试用图像法分析解答,以得到一种直观、简便的解题方法.
1 “子弹打木块”模型的两种典型情况
物理过程:子弹质量为m,木块质量为M,木块长度为L,木块静止放在光滑的水平面上,子弹以速度v0水平射向木块,在整个过程中木块对子弹的阻力为恒力F.
1.1 子弹射入木块未穿出
(1) 描画物理过程(如图1).

图1
(2) 描画物理图像(如图2).
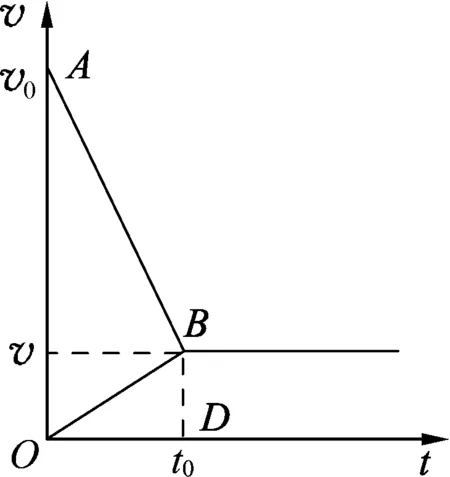
图2
(3) 物理图像的物理意义.
图2中,木块的v-t图线OB的斜率大小表示木块匀加速运动的加速度的大小;子弹的v-t图线AB的斜率大小表示子弹匀减速运动的加速度的大小;子弹的v-t图线与横坐标轴所包围的面积的大小表示子弹位移的大小s1;木块的v-t图线与横坐标轴所包围面积的大小表示木块位移大小s2;△ABO的面积s3=s1-s2表示子弹射入木块的深度d;v为子弹、木块最终共同速度.
1.2 子弹射入木块穿出
(1) 描画物理过程(图3).
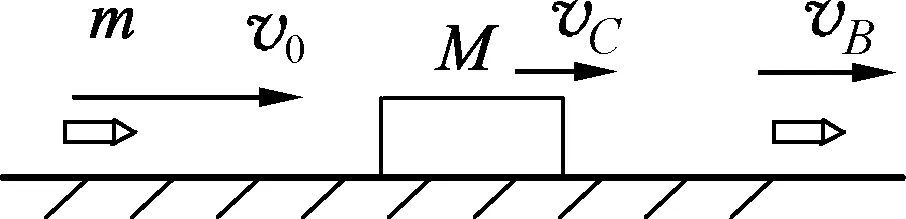
图3
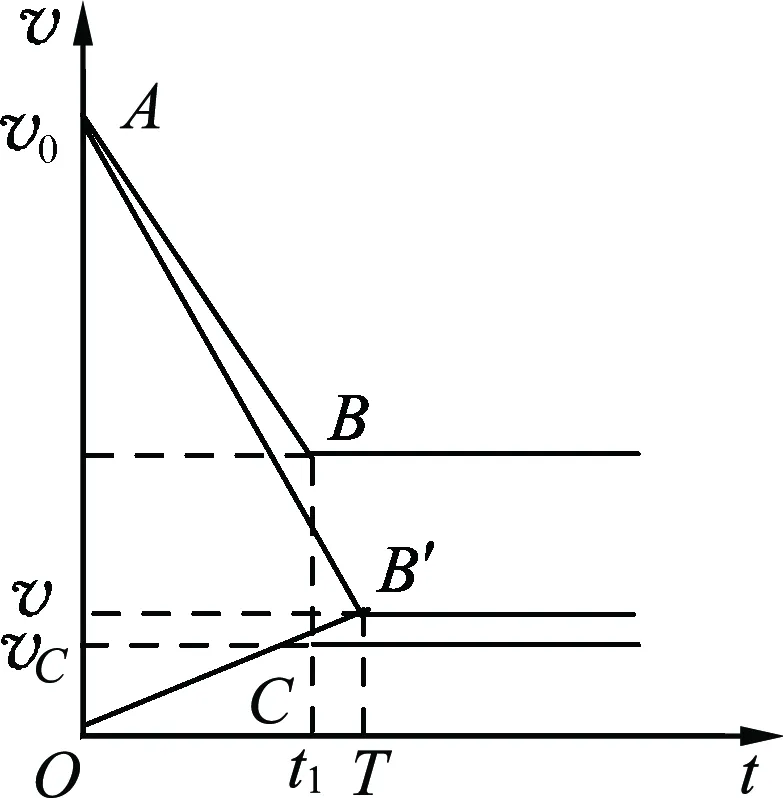
(2) 描画物理图像(图4).
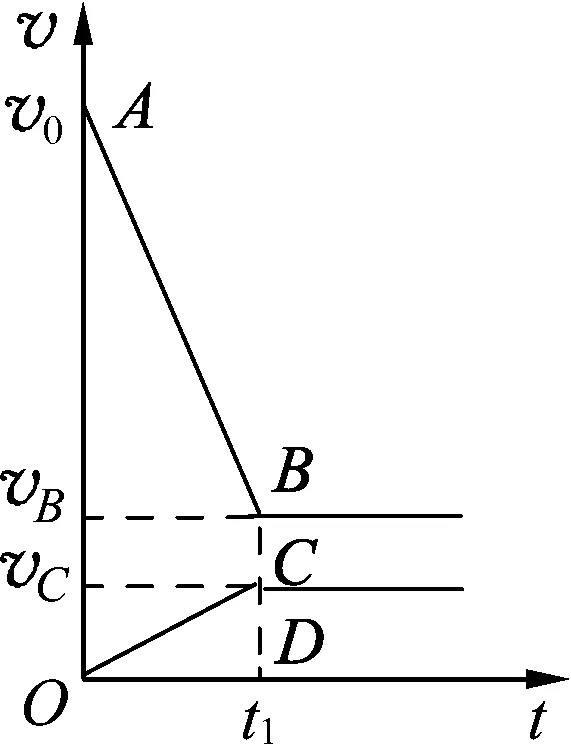
图4
(3) 物理图像的物理意义.
图4中,木块的v-t图线OC的斜率大小表示木块匀加速运动的加速度的大小;子弹的v-t图线AB的斜率大小表示子弹匀减速运动的加速度的大小;子弹的v-t图线与横坐标轴所包围的面积的大小表示子弹位移的大小s1;木块的v-t图线与横坐标轴所包围面积的大小表示木块位移大小s2;梯形ABCO的面积s3=s1-s2表示木块的最大长度L;vB,vC分别表示子弹、木块的最终速度.
2 “子弹打木块”类物理问题的图像解
2.1 判断子弹能否击穿木块的方法
“子弹打木块”类物理问题,一旦它们的初始条件确定,其能够穿透木块的理论深度是确定的,设为s.我们只须比较理论穿透深度s和木块的实际长度L即可确定子弹能否穿出木块.
在所给子弹初速,子弹质量,木块质量,木块对子弹恒定阻力条件下,子弹可贯穿木块的理论深度为s,理论贯穿时间为T,最后二者以共同速度v前进.如图2,由初始条件及物理过程可得
(1)
理论贯穿时间为
(2)
理论贯穿深度为△OAB的面积,即
(3)
从而得到子弹能否击穿木块的判别式:当s≤L时,子弹不能穿出木块;当s>L时,子弹能够穿出木块.
2.2 子弹不能击穿木块的情况
图像解法:其物理图像为图2.
(1) 子弹未射出木块,有s≤L,即
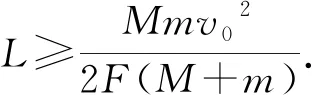
子弹贯入木块的实际深度d就等于子弹的理论贯穿深度.当等号成立时,子弹恰好运动至木块另一端,并且相对木块静止,子弹的理论贯穿深度即为木块长度.
(2) 子弹未射出木块,在木块中穿行时间t1≤T,即
(4)
最长相对运动时间为不等式取等号,为
(3) 子弹贯入木块的实际深度d为△OAB的面积s3,子弹对地位移为梯形OABD的面积s1,木块对地位移为△OBD的面积s2, 从图2我们还可以看出
s1>d=s3>s2.
(4) 子弹、木块相对运动过程中产生的热量为
相对静止时全过程产生的最大热量为不等式取等号,即Q=F·L.
(5) 二者最终共同速度根据公式(1)有
(5)
2.3 子弹能够击穿木块的情况
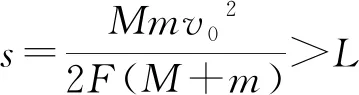
(1) 子弹能够穿透木块,子弹在木块中相对木块穿行长度为木块本身长度L.
(2) 图4中,梯形OABC面积为子弹击穿木块的深度,即木块的长度,等于L.
梯形OABC面积为
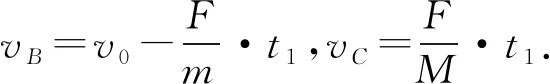
联立上述3式,解得
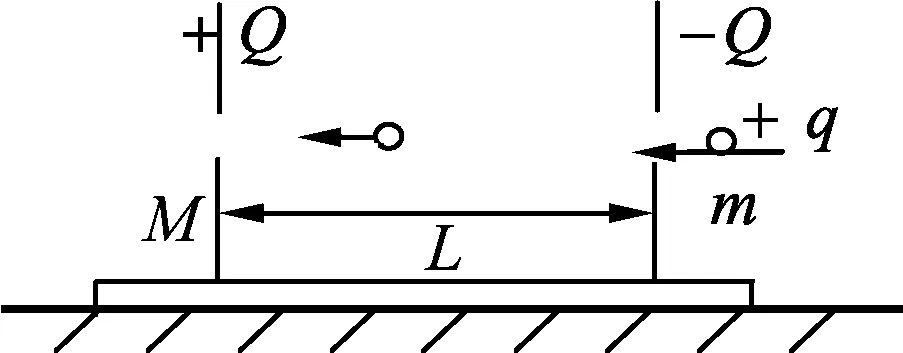
因为子弹能够射穿木块,所以实际贯穿时间小于理论贯穿时间,即应该t1 (6) (3) 子弹在木块中穿行,二者分离时子弹对地位移s1为梯形OABD的面积;木块对地位移s2为△OCD面积;子弹相对木块位移s3为梯形OABC的面积,根据图4有 s1>s3>s2. (4) 子弹穿出木块,产生的热量为Q=F·L. (5) 子弹在木块中穿行至分离时, 二者分离时,子弹相对木块运动时间为t1,将t1代入上述公式,得 (7) (8) 图像法能解决的物理问题,常规方法都能解.但图像法以它直观、简洁的特点远远优于常规方法.文中我们采用“图像、判别式方法”几乎可以解决内力为恒力的“子弹打木块”模型中所有物理问题,并且可以研究穿透过程的细节.但如果采用能量、动量来解题,因为此二者只解决始、终状态,如不告知子弹的最终状态,我们则必须采用试探解,过程将极为烦琐.当然,图像法必须在它的适应范围内才有效,对于内力为变力,或者只求子弹、木块最终共速时的速度,我们用动量方法即可.这也就启迪我们:任何一种方法都不是万能的,对于具体的物理问题,我们应该寻求最适合它的解答方法. 子弹质量m,以速度v0射入静止于光滑地面上的木块,其质量为M.木块长度为L,木块对子弹阻力恒为F,当子弹质量减小时,木块的速度将如何变化? 图像解析:根据2.1的判别式,结果有两种情况. 图5 图中AB为开始子弹入射木块至分离时的图线;AB′为子弹减小质量后恰好能够穿越木块的图线;木块质量不变,OB′为木块运动图线. 从数学上也可以判断,随着m减小,vC即木块速度将变大. 从图像和数学上都容易判断木块的最终速度将减小.整个过程中,当s=L时,木块的速度最大. 同样还可以判断:如果只改变木块的质量,比如变大或变小,其它条件不变,子弹以及木块最终的运动情况. 如图6所示,a、b是静止在光滑水平地面上的两块长木块.a的左端和b的右端相接触,二者等高.两木块的质量分别为Ma、Mb,长度分别为La、Lb,c是一个质量为m的小物体(可视为质点),现给它一个初速度v0,使它从b的左端开始向右滑动.已知c与a、b之间的动摩擦因数分别为μ2和μ1,求最后c以多大的速度运动. 图6 我们首先需要判断小木块在上述物理条件下的最终停留位置是在b上,还是在a上,或者最终c是否跃出a. 判断c能否滑出b.由所给的初始条件,当c在b上运动时,可以将b、a作为一个整体.根据公式(3)此时的理论贯穿深度为 其中F1=μ1mg. 当s1≤Lb时,小木块c将停留在b上; 当s1>Lb时,小木块c将滑出b.若c能够跃上a,则c刚跃上a时相对a的速度为v02=vB-vC.其中vB为c离开b时的速度;vC为b的最终速度,也即c跃上a时a的速度.c在a中的理论贯穿深度根据公式(3)为 其中F2=μ2mg. 当s2≤La时,c将停留在a上.当s2>La时,c将跃出a. 通过上述分析,我们发现题目的物理过程表面上涉及3个物体,实质上仍是两个两体问题的组合.只不过在运用理论贯穿公式时,对于第2次应用,应注意入射速度要作一个转换而已. (1)s1≤Lb,c停留在b上,实质是“子弹打木块”问题中的子弹停留在木块中,它们的共同速度即类同公式(5).只不过此处木块质量为(Mb+Ma),所以共同速度为 此即小物体c的最终速度. (2)s1>Lb且s2≤La,c停留在a上,从整个体系来看,这类似于3.1中加速度发生变化的情况.假设F1 图7 木块b、木块a共同运动v-t图线为OC线;c离开b而跃上a的瞬间开始,a运动的v-t图线为CD线;c在b上运动的图线为AB线,c在a上运动的图线为BD线. 我们发现: 当c将要离开b而跃上a的瞬间,b将以最大速度vC匀速运动;a将在速度vC的基础上加速前进,此时b,a分离.c最终停留在a上,二者以共同速度vD前进. 如果c刚跃上a时以此时的a为参照系,入射速度即为v02=vB-vC,对应木块质量为Ma,木块长度为La,a对c阻力为F2.它们的最终共同速度类同公式(5),为 对于公式(7)、(8),将M以(Ma+Mb)替代,L以Lb替代,即可得到本处所求的vB,vC,从而求得v02=vB-vC,最终得出vD′.将vD′叠加a的开始速度vC,即可得c的最终速度vD.即 vD=vD′+vC. (3)s1>Lb且s2>La,c冲出a,c的最终速度求解类似公式(7),唯一不同的是c跃上a时a有初始速度vC,c相对a的速度为v02,假设F1 图8 在3.2(2)中我们已经求出vC、vB.以c刚跃上a时的a为参考系,根据图8,c对a的最终速度vD′为 而根据公式(6)可得(t2-t1),将相关各式带入可以求得c的最终速度为:vD=vD′+vC. 例1.如图9所示,电容为C的电容器固定在绝缘木板上,总质量为M,木板置于光滑水平面上.两个极板竖直放置,极板带有电荷量Q,极板间距为L,在电容器右极板上有一个小孔,同时左极板对应位置也有一小孔.一个质量为m,带电量为+q的小球以速度v0从右小孔水平射入电容器中(不考虑小球的重力,电容器周围电场强度为0),并且从左小孔射出,试确定小球、电容器的最终运动情况. 图9 小球穿越电容器,应用公式(7)、(8)可得小球速度 电容器速度 例2.矩形大木块质量M=2 kg,长度L=1 m,静止放在光滑的水平面上.小木块(看作质点)质量m=1 kg,开始时置于大木块左上端,以初速度v0=2 m/s水平向大木块右端滑去.求: (1) 当二木块间动摩擦因数μ=0.1时,m、M的最终运动情况; (2) 当二木块间动摩擦因数μ=0.5时,m、M的最终运动情况.2.4 总结
3 “子弹打木块”模型图像解法的应用
3.1 对于加速度发生变化的情况
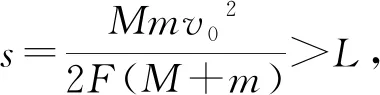
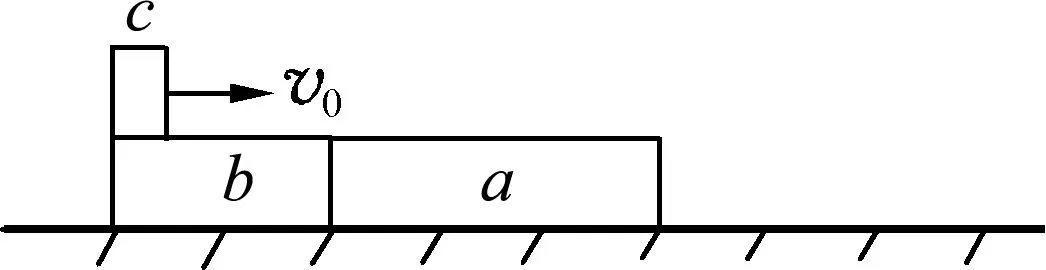
3.2 “子弹打木块”模型中的“三体问题”
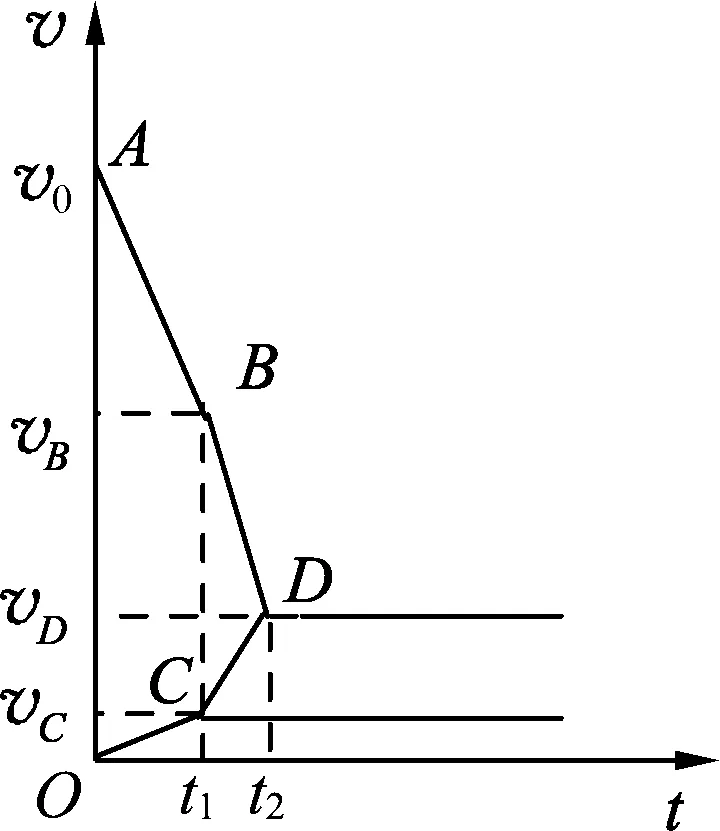
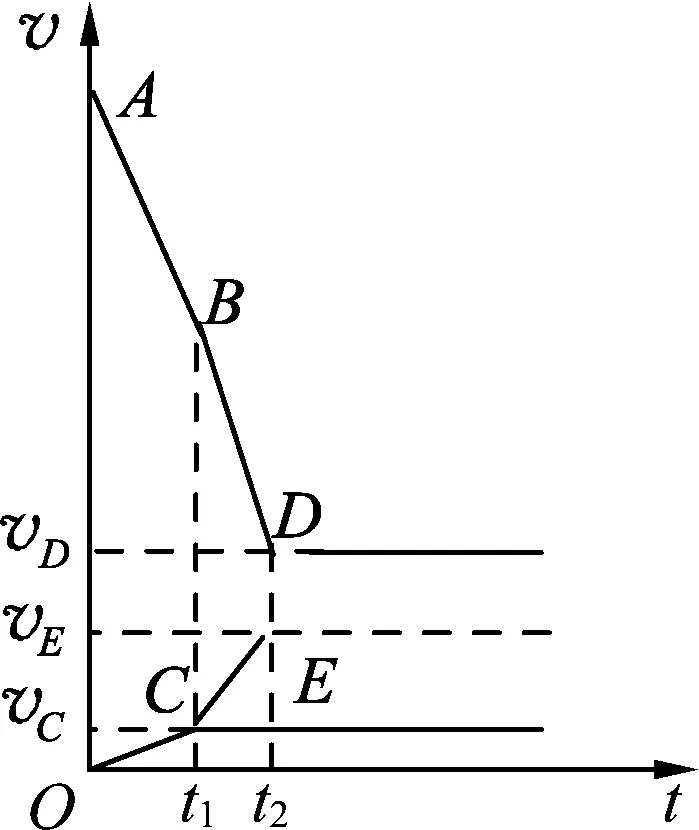
3.3 “子弹打木块”模型的应用