“三力”模型下篮球投篮最佳角度的实验研究

刘旭光，赵汝卿，张雅男

“三力”模型下篮球投篮最佳角度的实验研究

刘旭光1，赵汝卿2，张雅男3

1.南京信息工程大学体育部，江苏 南京，210014；2.南京信息工程大学长望学院，江苏 南京，210014；3.南京信息工程大学工程训练中心，江苏 南京，210014。

投篮时出手状态是指篮球的出手速度、出手角度及球的旋转速度。篮球的飞行轨迹与这些因素有关，“三力”模型以重力、空气阻力及玛格努斯力三种力为基础，推导动力学方程，利用仿真求解篮球的飞行轨迹，通过命中率得到投篮时的最佳出手状态。三力模型下，出手速度更快，投篮更用力，但后旋球会减小出手角度，达到省力的目的。通过计算出最佳出手状态，给出运动员平时训练的状态范围，可以指导训练，从而提高运动员在比赛时的命中率。

动力学方程；运动轨迹；玛格努斯力；最佳状态

1 问题的提出

篮球运动是以进球得分多少来评定胜负的体育运动，多数有关篮球运行轨迹的研究都是对提高投篮命中率的定性分析，或者基于篮球出手后仅受重力影响的轨迹方程分析。牛成龙、朱仁坤、许文斌等[1-3]分析了投篮的过程和影响命中率的各种因素，提出了技术因素、身体素质因素、心理因素和时空因素4个影响篮球命中率的因素，但仅限于定性分析，并没有给出定量的结果。石平、赵军[4]提出后旋可以使入射角最大化，并提高命中率。王成军等[6]考虑了前旋和后旋对篮球轨迹的影响，提出在行进间或在篮下，通过前旋可以缩短飞行距离，加快下落，提高空心入网的命中率；而通过后旋球则可使篮球在中远距离的投篮中增加稳定性和飞行时间，提高空心入网的命中率，但同样没有给出定量的结果。葛文中[5]分析了高度、距离和投射角对篮球命中率的影响，提出高度、距离和投射角的增加都对命中率有很大影响。

杨爱茜等[7]运用MATLAB软件对二次函数关系的篮球运动轨迹进行数据分析，采用控制变量法找出了出手速度、出手角度、水平距离和垂直高度等4个方面影响因素的最佳范围，但研究方法和结论都是基于篮球仅受重力影响的假设。高秀明等[8]通过变分法给出了抗角度偏差最佳角和最省力投篮角，提出当出手点和篮筐的连线正好为出手角的平分线时投篮的抗角度偏差最佳且最为省力；但没有考虑阻力和球的旋转带来的影响，同时也忽视了篮球入射截面对篮球入筐的影响。段然[9]对篮球入射角度进行了分析，通过入射截面的大小，给出了不同入射角投篮时可允许误差范围，并指出当入射角小于33°时篮球不可能入篮；同时，指出可通过后旋球增大篮球入射角从而提高命中率。但并没有考虑阻力所带来的影响。

本文根据实际情况，考虑重力、空气阻力以及玛格努斯力三种力同时存在时，建立“三力”模型，推导篮球飞行满足的动力学方程。通过模拟仿真计算，分析后旋球、前旋球及无旋球飞行轨迹，出手速度及角度之间的关系。根据不同投篮者的自身条件，具体讨论最佳的出手状态，以及训练时的出手状态范围。为了验证模型的有效性，通过蒙特卡洛方法将“三力”模型与“单力”模型的命中率进行对比。

2 运动中篮球的受力分析

在标准投篮过程中，运动员会通过一系列的连续动作将力从腿部沿腰部、大臂一直传导到手腕、手指，并最后将球“拨出”；有经验的运动员会通过控制手腕及手指的发力使得篮球产生旋转从而达到篮球在飞行中达到更稳定或飞行时间更长的目的。投篮命中率受较多因素的影响[13]，因而有必要对其进行理论分析，本文对篮球的受力进行了较为细致的分析，具体如下：

2.1 篮球在空中的受力分析

对于篮球初学者，不标准的投篮动作有点类似推铅球。手腕手指直接发力将球推出。这种情况下，篮球是无旋转或者旋转速度很小的在空中飞行。专业篮球运动员实际训练时，教练员都要求篮球运动员利用手腕手指将篮球“拨动”。即手腕发力，手指要与篮球有摩擦，篮球在空中飞行时，有一定的旋转速度。此时，将篮球作为质点分析其运动显然是不合适的。根据刚体力学，此时的篮球可以看成是刚体。在手指与篮球摩擦力的作用下，对篮球产生了转动力矩，可以简化为篮球刚体在做平面运动。篮球质心在做有阻力的抛物运动，篮球本身也在绕过球心的某条直径做转动。

为了更准确的分析篮球的飞行轨迹，假设篮球在飞行时受到重力、空气阻力、玛格努斯力。流体力学中，物体所受到的空气阻力与物体的速度有关。投篮后篮球飞行过程中，由于其速度相对而言较小，因此受到的阻力和速度可以看作成一次比例关系[8]，且阻力方向与速度方向相反[12]。即

玛格努斯力[9，11]是指物体因旋转而带动周围气流的流动，从而使得周边的气流流速不同，因而产生压强差，此压强差会产生一个垂直于物体运动方向的力，即玛格努斯力，其表达式为

2.2 篮球飞行的动力学方程

通过受力分析，建立篮球飞行时的运动学方程：

为了使方程形式简单，便于分析，将（4）式代入（3）式并分解为水平和竖直两个方向，可以得到下式：

3 仿真验证

3.1 方程的离散化

将上述方程（5）离散化，可得如下方程：

方程（6）在给定初值条件及边界条件后，即可求得篮球飞行到篮圈平面时的入射角，根据文献[9]的计算方法，利用篮球在篮圈平面的投影判断其是否命中。

考虑到球员在赛场上实际的投篮情况，常微分方程解得的轨迹最高点大于1.5的值均被舍去。其中，表示篮筐的竖直高度，国际标准取3.05m。

3.2 旋球对飞行的影响

利用前文所述模型，分别计算篮球前旋、无旋、后旋三种情况的飞行轨迹、飞行速度和出手角度之间的对比关系，结果如图1所示。图1a说明后旋球的飞行轨迹明显与无旋和前旋方式不同，并且入射角度相对较大；图1b显示，飞行同样距离，后旋球的飞行速度最小。图1c得到结论，飞行同样距离，后旋球所需出手角度最小。这些与现实经验相符的特点都可以用简单的物理原理解释，本文不再赘述。从已发表的文章中[9]可知，到达篮筐时入射角度越大，命中率越高。投篮以后旋球方式出手，会增大入射角度。但是否旋转速度越大就命中率越高呢？在考虑运动员的体能消耗时，投篮的出手角度和出手速度是否略作调整呢？这样的研究少有人涉及。本文正是根据现实中篮球飞行时受力情况，建立“三力”模型进行数值模拟，求解篮球飞行轨迹。在保证命中率基础上，讨论出手角度、出手速度以及篮球旋转之间的相互关系，试图对实际的篮球投篮训练给予理论性指导。

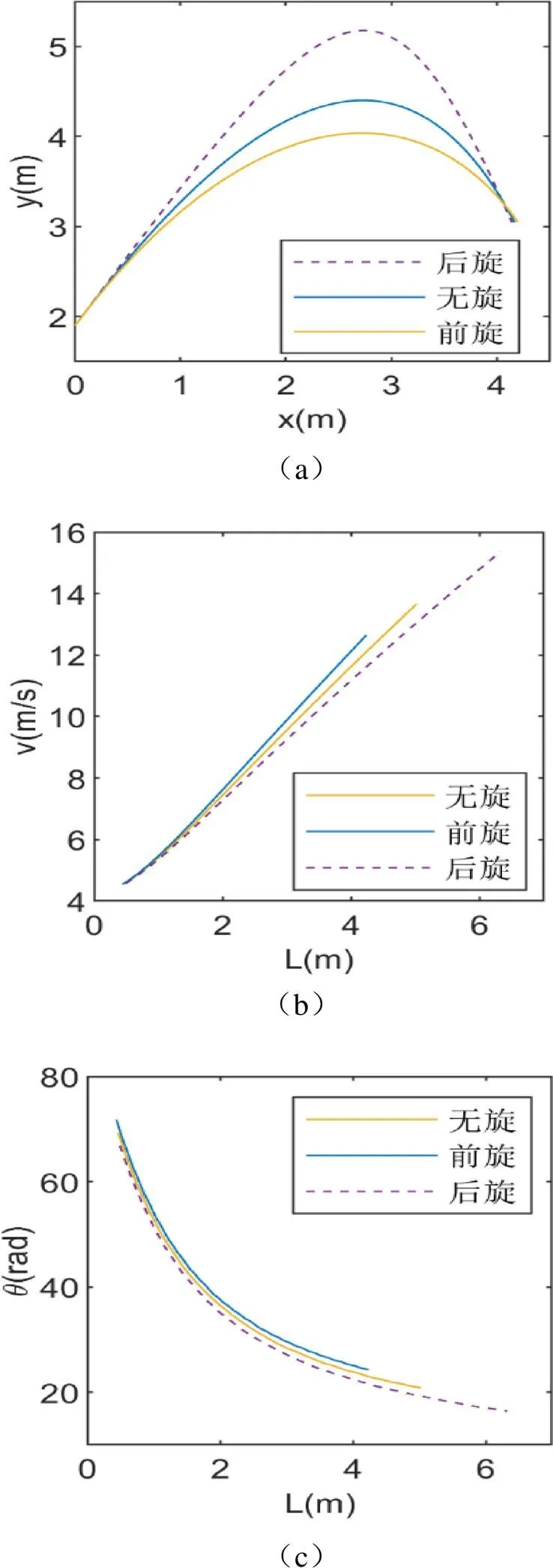
图1 后旋、前旋和无旋球的对比

（a）飞行轨迹 （b）飞行速度 （c）出手角度

3.3 三种因素对命中率的综合影响

3.3.1 最佳出手状态 现实中的投篮，不管是训练中，还是赛场上，命中率都受到很多因素的制约。本文建立的模型相较于其他研究，考虑更多的受力，与现实情况更符合。此外，只考虑一种因素对命中率的影响并不能指导平时训练。因为投篮时，通常都是多种因素影响命中率。而且，各种因素彼此之间也会相互干扰。本文建立“三力”模型，将出手速度，出手角度，篮球旋转角速度同时设定为影响投篮命中率的参量，通过计算，试图发现彼此之间的关系以及对命中率的综合影响。根据分析结果，用以指导篮球运动员的平时训练，使运动员在各种因素最适合的范围内加以练习，形成对身体肌肉的条件反射。这样，在比赛时，运动员的投篮命中率才能得以提高。

投篮者自身的条件并不相同，本文主要是讨论出手速度、出手角度及篮球旋转角速度对命中率的影响。因此，固定投篮者的出手高度=1.9m，以篮筐为中心点，以罚球线与篮筐距离为半径作半圆，投篮者位于半圆的任意位置上（投篮者与篮筐距离=4.325m）。

表1 命中率与出手状态

通过对比可以看出，低于模型计算出的最佳出手状态时，其命中率较低；而高于该速度的出手状态，则命中率几乎没有太大变化。因此，运动员以模型计算出的最佳出手状态范围进行训练，会获得最大的“性价比”。图3计算的结果是固定投篮者的身高，出手点高度，出手点离篮圈水平距离等因素，当投篮的条件变化时，可以求出不同的出手状态最佳训练范围，做到因人而异，因环境变化而改变。

图2 命中投篮的出手状态

图3 寻找最佳投篮状态范围

3.3.2 篮球的旋转速度分析 根据经验认为，篮球的旋转一定会提高命中率，但对此进行原理性分析以及比较旋球和非旋球命中率的研究却非常少见。本文3.2中只是简单讨论旋球有利于增大入射角度及减小出手速度和出手角度，但后旋球是否可以与其它因素同时影响命中率仍未给出明确的结论。表2中给出了具体的对比结果。可以明显看出，与前旋和无旋球相比，后旋球的确可以提高命中率。表中得到的较低命中率，是因为以无旋球最佳投篮状态为基准范围，选取了临近的三个范围求出平均命中率。此种比较只是为了显示后旋球对命中率的影响。如果以表1中后旋球最佳出手状态计算，命中率便会显著提高。

表2 旋球对命中率的影响

3.4 “三力”模型与“单力”模型对比分析

只考虑重力对篮球轨迹的影响，投篮轨迹需满足如下条件：

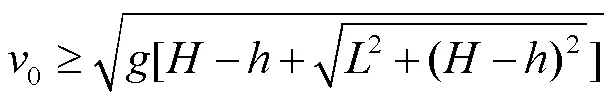
考虑到球性[14]对篮球投篮的影响，本文将“单力”（只受重力）和“三力”模型下相同出手角度和出手速度的命中率进行对比，结果如表3所示。分析时，选取了专业运动员和普通人在两种模型下命中率的对比。目的是证明本文模型也适用于普通篮球爱好者进行训练指导。考虑到专业运动员经过训练，出手状态的起伏要小于普通人。显然，“三力”模型的命中率要远远高于单力模型。而三分球命中率的降低是因为投篮距离较远，出手速度自然提高，出手力将迅速增大。此时无论是专业运动员还是普通篮球爱好者，即便是出手状态的起伏仍在5%和10%，但出手速度范围将扩大，导致命中率会降低，这也符合实际情况。

表3 “单力”模型与“三力”模型命中率比较

为何“三力”模型的命中率会更高，是因为其不仅考虑三种力作用在篮球上，更符合真实情况。同时，“三力”中的玛格努斯力是由于篮球因旋转而产生上下压强变化形成的力，这是前文比较后旋球、前旋球和无旋球的目的所在。图4中给出“单力”模型与“三力”模型在出手速度与出手角度方面的对比。以模型计算得到的命中投篮为样本，“三力”模型因为考虑力较多，相对出手速度大，更费力。但由于后旋球会减小出手角度，增大入射角度，这一特点却恰好可以弥补因出手速度大而耗费的体力。

图4 “单力”模型与“三力”模型出手角度与出手速度比较

4 总 结

篮球运动员平时训练主要目的是产生肌肉的条件反射，在任何距离投篮都要形成习惯。如果能以科学分析指导训练，则会事半功倍。本文建立“三力”模型，真实的反应了篮球飞行中的受力情况。将出手角度、出手速度及篮球旋转速度三种参数输入模型，通过命中率求解不同投篮距离时的最佳出手状态。通过对比，可以看出，在最佳出手状态附近范围内命中率最高，也最节约体力。而“三力”模型中的玛格努斯力是因篮球旋转而产生的，因此导致后旋球投篮可以增加命中率。“三力”模型与“单力”模型比较，精确的计算出了出手速度和出手角度的差别，并且命中率也有显著提高。

本文对投篮最佳状态范围的确定是以模型求解值为中心，以该值的5%为邻域，取随机正态分布而构成。自然，邻域范围也可以相对扩大，这样训练时的可以由大范围逐渐减小。本项工作受到南京信息工程大学大学生创新创业训练计划支持，后续工作以设计传感器为主要目标，可以实时的测量运动员投篮时出手速度、出手角度即篮球旋转速度，根据模型的理论结果，对运动员的训练给予监测和指导。

[1] 牛成龙，赵世鹏，樊腾龙，等.篮球跳投技术的运动生物力学分析[J].青少年体育，2017（02）：46～47.

[2] 朱仁坤，王文锦，殷晓岩.篮球训练中提高三分球投篮命中率的对策研究综述[J].当代体育科技，2018（36）：31～33.

[3] 许文彬.如何提高单手投篮的命中率[J].上海体育学院学报，1981（01）.

[4] 石 平，赵 军.试论球的后旋对提高投篮命中率的作用[J].上海体育学院学报，1987（01）：65～68.

[5] 葛文中.投篮出手高度与出手角度对命中率的影响[J].上海体育学院学报，1980（04）：80～83.

[6] 王成军，郑 旗.篮球的旋转对提高投篮命中率的力学分析[J].体育研究与教育，2012（02）：100～104.

[7] 杨爱茜，李 辉.基于MATLAB对篮球运动轨迹的仿真研究——篮球运动轨迹理论性分析[J].体育科技，2015（05）：27～29.

[8] 高秀明，苏永福.用变分方法研究篮球投篮最佳出手角[J].数学的实践与认识，2008（06）：143～150.

[9] 段 然.篮球投篮运动轨迹与命中率的物理模型[J].科技创新导报，2009（20）：242～243.

[10] 李武钢，张彬玲.基于信息技术测量篮球的空气阻力系数[J].物理与工程，2012（03）：31～33.

[11] 潘慧炬.马格努斯效应的力学模型[J].浙江体育科学，1995（03）：16～19+61.

[12] 余 万，李 春，任 杰，等.基于计算流体力学方法的乒乓球轨迹仿真[J].上海体育学院学报，2017，41（03）：89～94.

[13] 戴 勇.影响高水平篮球运动员罚球命中率的因素及相关的心理训练[J].上海体育学院学报，2003（06）：35～36.

[14] 克劳斯.巴克豪斯本德.埃里克森. 多元统计分析方法（用SPSS工具）[M]. 格致出版社，2009.

Research on the Best Shooting State Based on the “Three Forces” Model

LIU Xuguang1, ZHAO Ruqing2, ZHANG Yanan3

1.Nanjing University of Information Science&Technology, Nanjing Jiangsu, 210014, China;2.Nanjing University of Information Science&Technology, Nanjing Jiangsu, 210014, China;3.Nanjing University of Information Science&Technology, Nanjing Jiangsu, 210014, China.

The shooting state during shooting refers to the basketball's shooting speed, shooting angle and the ball's rotation speed. The basketball flight path is also related to these factors. based on the three forces of Gravity, Air Resistance and Magnus Force, the "Three Forces" model is established, the Kinetic equations are derived, the basketball flight trajectory is solved by simulation, and the best shot state when shooting is obtained through the hit rate. In the “Three Force” model, the shot speed is faster and the shot is harder, the backspin will reduce the angle of the shot and achieve the goal of saving effort. By calculating the best shot state and giving the athlete's usual training state range, you can guide the training, thereby improving the athlete's hit rate during the game.

Kinetic equations; Trajectory; Magnus Force; Best state

1007―6891（2021）05―0057―05

10.13932/j.cnki.sctykx.2021.05.13

G841

A

2020-11-30

2021-01-07

南京信息工程大学大学生创新创业训练计划项目（课题编号：201910300292）。