黄河下游利津断面年径流量预测研究

杜 懿，王大洋，林泳恩，王大刚

(中山大学地理科学与规划学院，广东 广州 510275)

众所周知，中长期径流预报对于区域或流域的水资源规划和管理具有重要意义，可靠的预测模型可为相关部门在水库调度、水资源配置、水利工程运行等方面提供决策指导[1]。然而，由于径流时间序列具有高度的非线性和随机性特征，传统预报方法往往很难取得满意的效果。比如自回归类模型、灰色模型、集对分析模型和马尔科夫链模型等针对于平稳水文时间序列一般表现较好；而对于具有趋势变化特征的非平稳时间序列，预测误差往往较大。机器学习模型如人工神经网络、支持向量机、随机森林等虽然具有强大的非线性拟合能力，但是容易忽略序列自身所隐含的连续性和相依性，而将其简单视作为纯随机序列，模型表现通常也不尽如人意。

“分解-预测-重构”思想的提出为解决这一问题提供了新的途径，其本质是将信号分解方法与时间序列分析方法进行联合[2-3]。该类方法总体表现出色，可有效提高模型的预测能力。基于此，国内外学者进行了大量研究，马细霞等[4]于2008年利用结合DB4小波分解的SVM模型对某水库的月径流进行了预测研究，结果表明模型预测效果较好；钱晓燕等[5]于2010年提出了EMD与LS-SVM的耦合预测模型，并对紫坪铺水文站的年径流进行了预测，结果表明耦合模型的表现要优于LS-SVM模型；覃光华等[6]于2013年建立了小波分析与GRNN联合的预测模型，在对三皇庙水文站年径流的预测研究中发现，该组合模型的预测能力较传统方法更好；2015年，张洪波等[7]构建了基于EMD的RBF预测方法，在对渭河流域降雨和径流的预测研究中发现，该方法适用于具有强趋势变化的非平稳时间序列；2016年，马超等[8]基于EEMD-ANN模型对三峡水库的年径流进行了预测，并将预测结果与自回归模型和人工神经网络模型进行了对比，预测误差明显减小；2018年，杜懿等[9]建立了WA-ARIMA和EMD-ARIMA组合模型，在对南宁市年降水量的预测研究中发现，两种模型的预测精度相较于ARIMA模型均有明显提高；桑宇婷等[10]于2019年建立了CEEMD-BP模型用于汾河上游的月径流预测，并与BP模型和EMD-BP模型进行了对比，结果表明该模型的预测精度最高；ZHANG等[11]于2020年利用MEEMD-ARIMA组合模型对黄河下游年径流进行了预测研究，结果发现该模型要优于EEMD-ARIMA模型和CEEMD-ARIMA模型；2020年，李文武等[12]提出了VMD和深度门控神经网络相结合的组合预测模型，结果表明，所建模型与单一模型以及其他组合模型相比，预测误差最小。

以上研究在建立组合模型时，信号分解方法的选取较为单一，一般只采用了一种或最多三种方法用于目标信号的分解，没有进行过不同种类下的多种分解方法的相互比较。鉴于此，本文在构建组合预测模型时，分别采用了WA、EMD、EEMD、CEEMD、MEEMD、VMD等两类共6种信号分解方法，尽可能优选出最佳组合模型，以提高预测精度。

1 研究数据

利津水文站为黄河最下游水文站，是全国大江大河重要水文站,,始建于1934年6月，1937年11月因抗战停测，后于1950年1月重新设站。站址位于山东省东营市利津县利津镇刘家夹河村，现隶属于黄河水利委员会山东水文水资源局，主要用于监测黄河入海水量、沙量，为黄河下游防洪、防凌以及水资源调度等提供水情资料。黄河流域3大主要控制断面从上往下依次为兰州断面(103.49°E，36.04°N)、花园口断面(113.39°E，34.55°N)和利津断面(118.18°E，37.31°N)，利津断面年径流变化过程见图1。

图1 1952年～2018年黄河利津断面年径流变化过程

由图1可见，1952年～2018年间黄河利津断面年径流序列存在较为明显的下降趋势，为一典型非平稳过程。鉴于自回归类模型对非平稳时间序列的预测效果较差，本文考虑借助机器学习模型来进行该非平稳时间序列的预测研究。

2 研究方法

2.1 信号分解方法

目前，常用的信号分解方法主要有小波分解及模态分解两大类。水文时间序列中常用的小波函数有Harr小波、Morlet小波、Daubechies小波和Symlets小波，考虑到Daubechies小波应用最为广泛，本文选用DB4小波分析来对目标序列进行分解。模态分解类方法主要包括有经验模态分解(EMD)、集合经验模态分解(EEMD)、互补集合经验模态分解(CEEMD)、改进集合经验模态分解(MEEMD)以及变分模态分解(VMD)。下面对各模态分解方法进行简单介绍。

EMD是由Huang等于1998年提出的一种新型自适应信号时频处理方法，该方法依据序列自身的时间尺度特征来进行信号分解，能够得到多个具有物理意义的固有模态函数和一个具有单调特征的趋势项[13-14]。鉴于EMD分解过程中存在模态混叠现象，Huang等在2009年又提出了EEMD，该方法可以有效改善模态混叠现象[15-16]。针对EEMD重构误差大等问题，Yeh等于2010年提出了CEEMD，该方法通过添加成对的符号相反的白噪声到目标信号，大大减小了重构误差[17-18]。由于EEMD和CEEMD中添加了高斯白噪声，导致计算量增大，郑近德等在2013年又提出了MEEMD，该方法在CEEMD的基础上结合了排列熵算法，利用排列熵算法对时间序列变化敏感的特性来检测信号的随机性，既抑制了模态混叠现象，又减小了计算量[19]。CEEMD虽然减小了白噪声引起的误差，但分解后会存在虚假模态，影响算法的精确度，基于此，Dragomiretskiy等于2014年提出了一种新的信号分解方法，即VMD，该方法可以实现固有模态函数的有效分离，表现出了更好的噪声鲁棒性[20]。

2.2 支持向量机

支持向量机(Support Vector Machine，SVM)是由Vapnik等于1995年提出的一种基于统计学习理论的机器学习算法，能够有效解决“非线性”、“过学习”、“维数灾”等难题，为小样本机器学习问题提供了一个较好的理论框架[21-22]。

本文基于LIBSVM开源工具箱来实现SVM模型的构建，该工具箱提供了许多默认参数，当使用RBF作为核函数时，模型需要优化的参数主要有c、g、p。为了尽可能高效、客观地寻找到模型的最优参数组合，采用遗传算法来进行参数寻优。寻优过程中，参数c、g、p的初始取值范围分别设置为[0，100]，[0，1 000]，[0，1]，种群规模取为20，最大进化次数设为300，并以模型训练期的均方根误差最小为目标函数。需要说明的是，以下所有方案中的预测模型，均以GA-SVM为基模型。

2.3 评价指标

为了能够较为准确、全面地对各个模型的预测能力进行评价，选取了合格率(Qualified Rate，QR)，平均绝对百分比误差(Mean Absolute Percentage Error，MAPE)和均方根误差(Root Mean Square Error，RMSE)共3个指标，计算公式如下

QR=(n/N)×100%

(1)

(2)

(3)

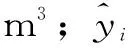
3 研究结果

3.1 方案一

水文时间序列自身存在着一定的相依性和连续性，序列的未来状态与当前及过去状态之间存在着某种联系，因而可以考虑利用序列自身所隐含的规律来预测未来的发展趋势。

为准确识别过去多长时间尺度的状态对当前状态的影响最为显著，综合采用自相关分析及Morlet小波分析来确定利津断面年径流序列的最佳自回归阶数，进而用于指导GA-SVM预测模型的构建。

图2显示，当滞时大于3 a后，利津断面年径流序列的自相关图开始逐渐呈现出拖尾现象；图3显示，3 a为利津断面年径流序列的一个小尺度周期。综合来看，可以确定利津断面年径流序列的最佳自回归阶数为3。

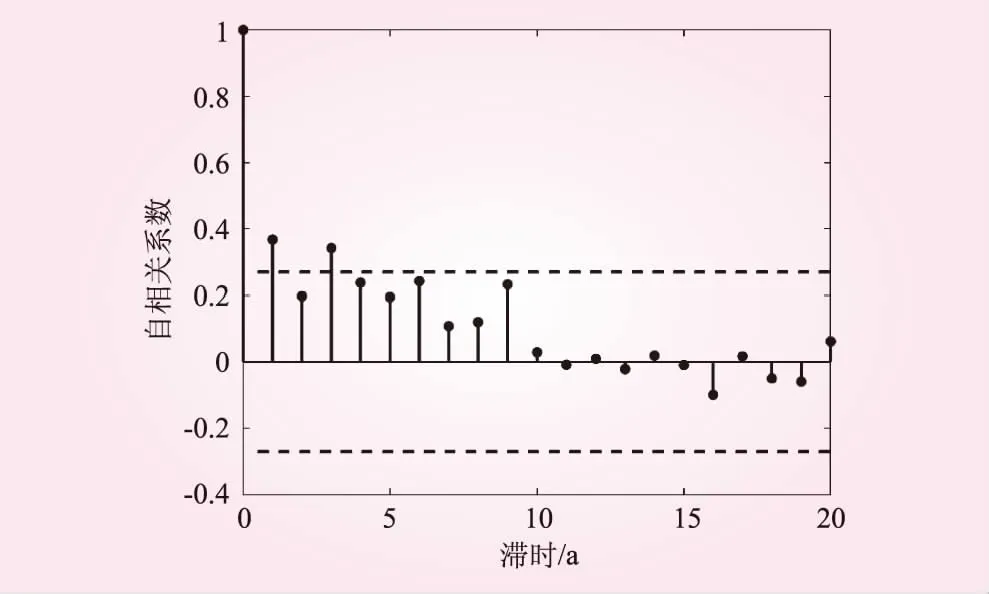
图2 利津断面年径流序列的自相关系数

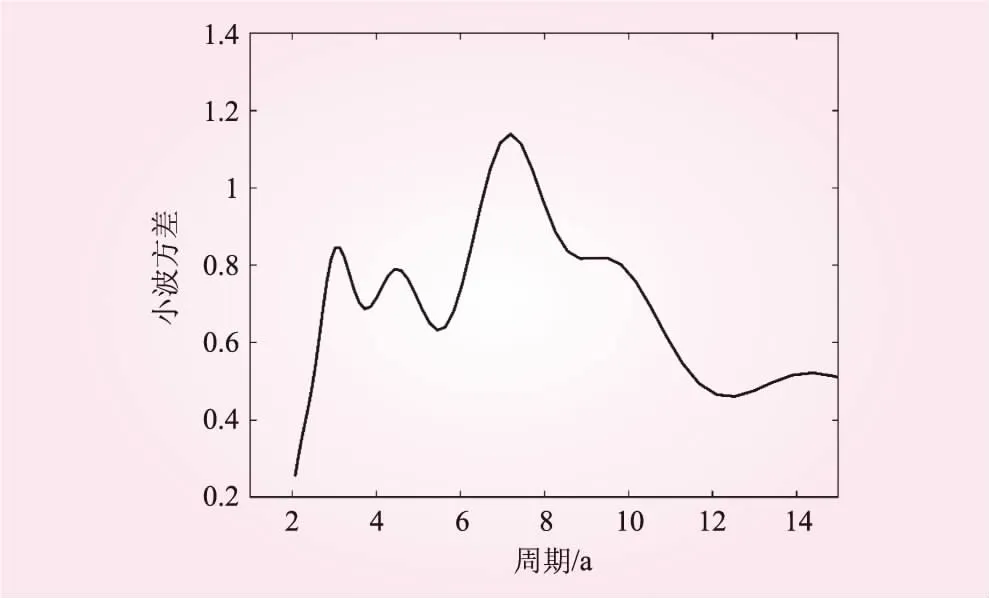
图3 利津断面年径流序列的小波方差

基于方案一，在建立GA-SVM预测模型的过程中，将Qt-3、Qt-2、Qt-1作为模型的输入，将Qt作为模型的输出。其中，t为预测年份；Q为年径流。经整理，共得到64组样本，将前50组样本作为模型的训练集，后14组样本作为模型的验证集，并利用上述指标对模型表现进行评价。

3.2 方案二

由于天然河道中的水量存在着空间连续性，同一河道内不同位置断面间的径流量存在着一定的相关性。基于此，可以尝试利用黄河上游兰州断面的径流量Qup，t来预测下游利津断面的径流量Qdown，t。

3.2 方案三

在方案二的基础上，将黄河中游花园口断面的年径流Qmid，t也加入到模型输入中，即同时利用上游兰州断面的年径流Qup，t和中游花园口断面的年径流Qmid，t来预测下游利津断面的年径流Qdown，t。

经整理，方案二和方案三均可得到67组样本数据，将前50组样本(1952年～2001年)作为训练集，后17组样本(2012年～2018年)作为验证集来建立预测模型，并利用评价指标对各个方案的预测效果进行检验，结果如表1所示。

由表1可见，仅利用利津断面自身的径流信息来建立预测模型，效果并不理想，验证期内的合格率仅为57.14%，模型尚未达到合格水平。方案二中，由于模型的输入增加了兰州断面的径流信息，因而模型的预测精度有了一定提高，相较于方案一，不仅平均绝对百分比误差有所降低，合格率也由原来的57.14%上升到76.47%，模型表现合格。方案三中，同时将上游兰州断面和中游花园口断面的径流信息作为模型输入，模型的预测精度得到了较大程度的提高，训练期和验证期内的平均绝对百分比误差仅有1.98%和3.42%，验证期内的模型合格率高达94.11%，模型表现优秀，模拟精度较高。

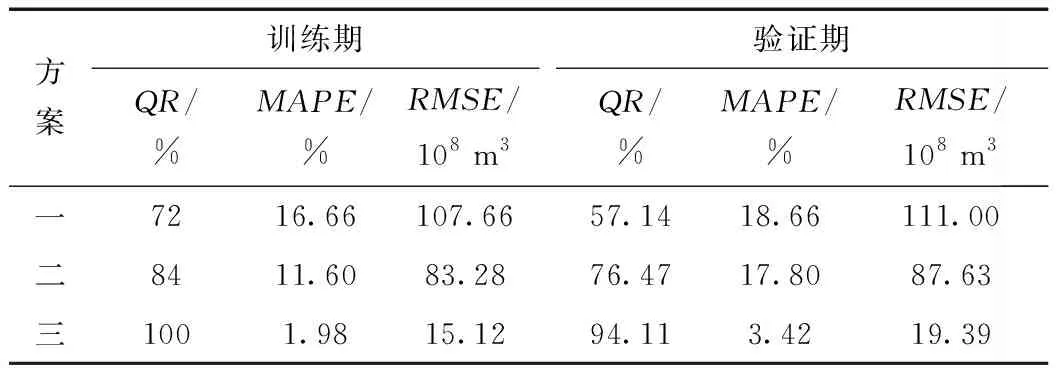
表1 3种预报方案的预测效果对比

3.4 方案四

鉴于方案一的预测效果并不理想，在不额外增加模型输入信息的同时为提高预测精度，将信号分解技术与方案一进行组合，制订出了方案四。其主要步骤为：

(1)分别使用DB4小波、EMD、EEMD、CEEMD、MEEMD、VMD等信号分解方法对黄河利津断面年径流量序列Yt进行逐层分解，得到n个具有不同频率尺度的子序列y1t，y2t，…，ynt。

(2)将每个子序列均看作成独立的时间序列，参照方案一的建模过程，训练得到n个基于GA-SVM的预测模型。

(3)将全部子序列的预测结果进行求和叠加，即可得到重构后的预测径流Xt。

(4)综合比较DB4小波、EMD、EEMD、CEEMD、MEEMD、VMD等6种信号分解方法的改进效果，确定最优改进模型。

方案四的技术路线见图4。

图4 方案四的技术流程示意

图5显示的是6种信号分解方法对黄河利津断面年径流序列的分解结果。对比6种分解方法得到的趋势项可以看出，1952年～2018年间黄河利津断面的年径流呈现出较为明显的下降趋势，这与前面的分析结论一致。下面以EMD分解结果为例，详细介绍EMD-GA-SVM模型的构建过程。

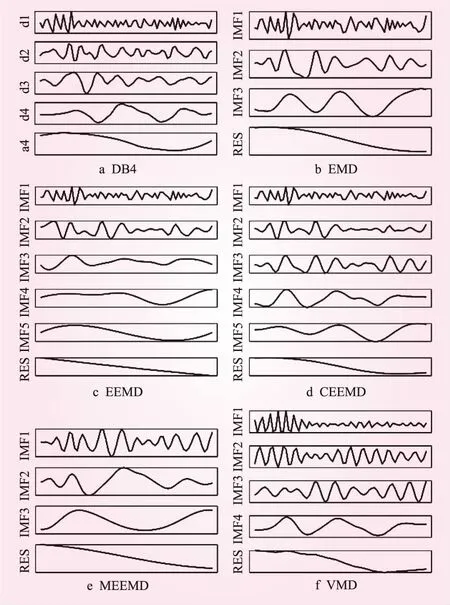
图5 利津断面年径流序列的分解结果

(1)对利津断面1952年～2018年的径流序列进行经验模态分解，分别得到了三个本征模态分量IMF1、IMF2、IMF3和一个趋势项RES。

(2)以IMF1为基序列，分别取基序列1952年～2015年的样本为序列X，取1953年～2016年的样本为序列Y，取1954年～2017年的样本为序列Z，取1955年～2018年的样本为序列T。

(3)将X、Y、Z作为输入，T作为输出，建立GA-SVM预测模型，建模过程中，取前50组数据为训练集，后14组数据为测试集，并将模型的预测值记为y1。

(4)同样地，依次将IMF2、IMF3、RES等作为基序列，重复步骤(2)和(3)，并将预测值分别记为y2、y3、y4。

(5)对y1、y2、y3、y4进行累加，结果即为EMD-GA-SVM模型的预测值。

方案四中不同改进模型的预测结果见表2。由表2可见，方案四中的全部预测模型均表现良好，验证期内的合格率均超过70%，平均绝对百分比误差均低于15%。对比6种组合模型， VMD-GA-SVM、MEEMD-GA-SVM、CEEMD-GA-SVM的合格率较高，均超过了90%；VMD-GA-SVM、CEEMD-GA-SVM、MEEMD-GA-SVM的平均绝对百分比误差较小，均低于10%。综合来看，VMD-GA-SVM模型表现最为优秀，精度最高，误差最小。

表2 方案四中不同改进模型的预测效果对比

图6显示的是4种方案的预测效果对比，除方案一外，其余3种方案的预测表现均较好，以方案三最好。利用信号分解技术对方案一进行改进后，模型的预测能力有了大幅提升，高于具有更多输入信息的方案二，略微低于方案三。

图6 4种方案下的预测模型模拟效果对比

4 结 论

(1)基于GA-SVM模型共制定了4种方案来对黄河下游利津断面的年径流量进行预测，结果表明，方案三中的预测模型模拟精度最高，验证期内的平均绝对百分比误差仅为3.42%，合格率达94.11%。

(2)由于方案一中仅使用了利津断面自身的径流信息来构建模型，因而模型误差较大。为提高预测精度，方案四中对原始模型进行了改进，主要是对输入数据进行了预处理，共构造了WA-GA-SVM、EMD-GA-SVM、EEMD-GA-SVM、CEEMD-GA-SVM、MEEMD-GA-SVM、VMD-GA-SVM等6种组合模型。研究发现，模型精度得到了明显提升，验证期内的平均绝对百分比误差均低于15%，合格率均超过70%。其中，以VMD-GA-SVM模型表现最佳，验证期内模型合格率达到100%，平均绝对百分比误差下降到7.17%。

(3)对比方案一、二、三可以发现，在使用机器学习模型预测水文时间序列时，随着输入信息的增加，模型的精度也得到不断提升；对比方案二和四，方案四的输入信息更少而预测精度更高，说明利用信号分解技术进行预处理可以有效挖掘出时间序列的隐含信息，弥补输入信息的不足，提高模型的预测能力。