考虑应力敏感的致密气藏动态产能方程及应用

2021-09-16赫文昊和向楠

非常规油气 2021年4期

赫文昊，魏虎，和向楠，王凯，李涛

(陕西延长石油(集团)有限责任公司研究院，西安 710075)

0 引言

致密气藏单井产量低，生产压差大[1-3]，普遍存在应力敏感性[4]。气井生产过程中地层压力不断下降，气体黏度和偏差因子均发生变化;同时由于储层存在应力敏感性，其净应力增大会导致储层渗透率下降。在建立气井产能方程时均需考虑上述因素。肖文联[5]采用变围压测定应力敏感的方法，利用低渗透储层岩心实测数据，回归得到应力敏感性幂函数经验关系式。宋传真[6]等建立了考虑应力敏感的拟稳态产能方程，但由于定容气藏在开发过程中地层压力不断下降，气体高压物性参数发生变化，生产初期的拟稳态产能方程已不适用于稳产期末地层压力的计算。庄惠农[7]提出了稳定点产能二项式方程并建立了动态产能方程，但未考虑储层应力敏感性。因此，该文建立了考虑应力敏感的致密气藏动态产能方程，详细描述了以该方程为基础的气井稳产期计算方法。使用该方法进行了实例计算，并利用气井实际稳产时间进行了验证。

1 致密气藏岩石应力敏感性

1.1 岩石应力敏感性分级评价

岩石应力敏感损害程度可采用净应力变化前后的岩心样品渗透率变化率来衡量[8]。

计算公式为:

式中:Dst，n为净应力变化前后的岩心样品渗透率变化率，%;K i为岩心样品初始渗透率，mD;K n为应力变化后再恢复到初始净应力时的渗透率，mD。

根据石油行业标准SY/T 5358—2010，岩心样品应力敏感损害程度分为5个等级，具体指标如表1所示。针对延安气田Y区块山西组山2段储层，共选取5井8个岩心样品进行应力敏感实验研究，如表2所示。

表1 应力敏感性损害程度评价等级[9]Table 1 Evaluation grade of stress sensitivity damage degree[9]

表2 岩心样品应力敏感实验数据Table 2 Stress sensitive experimental data of core samples

实验方法依据石油行业标准SY/T 5358—2010，采用围压变化的方式模拟致密砂岩气藏储层岩石承受净应力的变化。岩心样品取样深度为2 535～2 971 m，地面空气渗透率为0.025～0.094 mD，岩心样品孔隙度为3.46%～6.44%。

由表2可知，延安气田Y区块山2段储层存在应力敏感性，应力敏感性渗透率不可逆损害率为46.9%～59.6%，平均损害率为52.6%，应力敏感损害程度属于中等偏强。

1.2 应力敏感渗透率经验公式

岩石应力敏感性实验结果中，不同净应力ΔP对应不同的渗透率K。为了表达岩心样品的渗透率变化程度[10]，对应力变化后的渗透率K n进行无因次化处理，无因次渗透率表达为K D=K n/K i。

为取得岩心样品渗透率与净应力的关系[11]，对无因次渗透率与净应力进行幂函数回归，获得公式K D=ΔP-m。无因次渗透率与净应力相关的幂函数公式为:

式中:K i为气藏初始条件下的渗透率，mD;K n为地层压力P的渗透率，mD;Pi为气藏原始地层压力，MPa;P为目前地层压力，MPa;m为应力敏感系数。

不同区域的储层岩石受到的沉积、压实、成岩作用存在差异性，这导致每块岩心样品呈现出不同的应力敏感性[12]，即不同的岩心幂指数m存在差异性。岩心样品应力敏感性强度与幂指数m呈正相关的关系。岩心样品应力敏感实验幂指数回归关系式见表3。

表3 岩心样品应力敏感实验幂指数回归关系式Table 3 The power exponential regression relationship of the stress-sensitive experimental data of core samples

由回归公式得知，应力敏感系数m为0.231 1～0.305 8，平均值为0.297 3。对于同一地区同一层位，应力敏感系数可采用同一值。

2 考虑应力敏感的非达西流产能方程

气体高速非达西渗流的Forchheimier二项式方程为[13-15]:

气体在储层中径向流动的渗流速度为:

地层状态下气体的密度为:

气体在地层中流动的湍流表征系数为:

式中:μg为气体黏度，mPa·s;K为岩石渗透率，mD;q g为地层状态下的气体流量，m3/s;P为压力，Pa;ν为气体的渗流速度，m/s。

将式(4)、式(5)、式(6)代入式(3)中，并改为矿场单位制，可得:

式中:μg为气体黏度，mPa·s;K为岩石渗透率，mD;q g为地层状态下的气体流量，104m3/d;P，T为地层条件下的压力和温度，MPa，K;Psc，Tsc为地面标准状态下的压力和温度，0.101 MPa，293 K(20℃)。

将式(2)代入式(7)，分离变量、积分(μg和Z做简单处理，取平均地层状态时的和)。由于1/re极小，故忽略该项。将地层近井地带的污染考虑在内，其拟稳态渗流二项式产能方程为[16-18]:

其中:

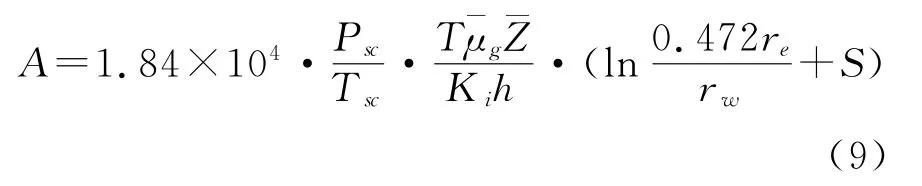
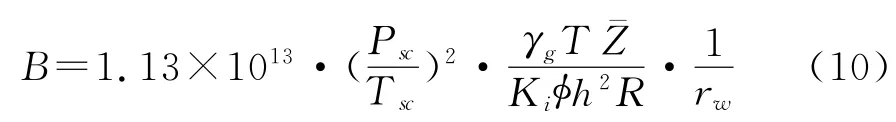
式(8)还可以表示为:

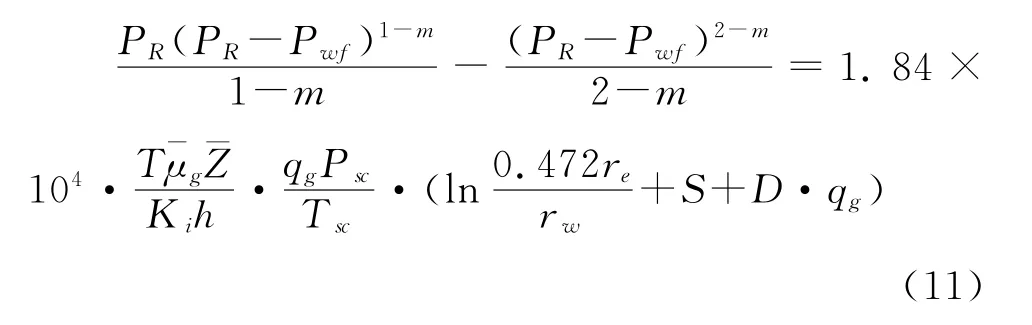
其中:

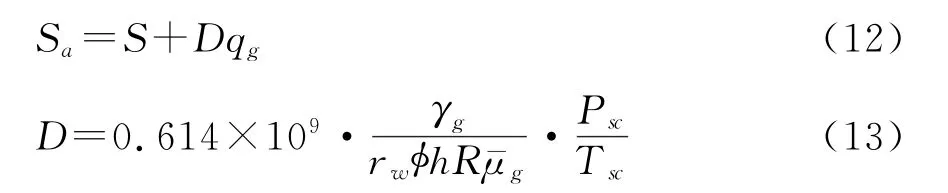
式中:Sa为视表皮系数;S为机械表皮系数;D为非达西流系数，(104m3/d)-1。

3 考虑应力敏感的动态产能方程及稳产期预测

气井稳产期末时，其地层压力已较大幅度低于初始地层压力，储层渗透性及天然气的和已发生变化，气井产能方程也相应发生变化。需要获取稳产期末时的和来计算新的产能方程[19-21]。

按照修正等时试井的工作制度，交替开关井4次。每次开井时气井产量为q gi，井底流压为p wfi，开井前关井恢复的最高地层压力为P Ri[22]。

式(8)可变形为:

其中:

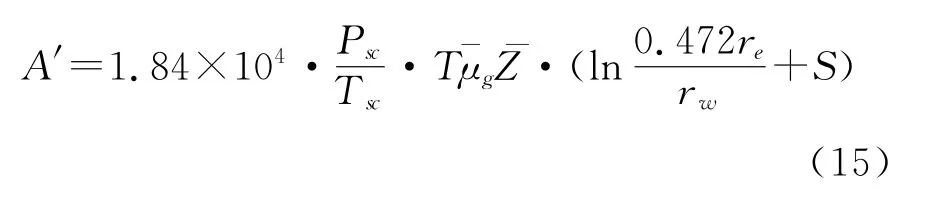
修正等时试井过程中，每个工作制度生产24 h后，均会关井24 h进行压力恢复。分别对4次关井压力恢复进行不稳定试井分析，可以解释得到相应的视表皮系数Sa。根据式(12)，对视表皮系数Sa与相对应的天然气产量q g线性回归，可得到D，S值。

修正等时试井延续流生产阶段天然气黏度和偏差因子分别取平均值和，与地层温度T以及前述非达西流系数D，一并代入式(16)即可求得B′。修正等时试井计算可得B值，两值相除B/B′，即可求得该井的初始地层系数K i*h。

重复以上迭代计算，当PRn-P R(n-1)＜ξ(ξ=0.1 MPa)时，则认为P Rn为稳产期末的地层压力。将PRn对应的及Ki*h和S，D，T带入式(11)，可获得稳产期末的产能方程。

利用流动物质平衡法，可以计算得到该井的动态地质储量Gs。根据定容气藏物质平衡方程:

式中:Pi为生产前地层压力，MPa;Zi为生产前气体偏差因子;Gp为累产气量，104m3;Gs为动态地质储量，104m3。

将稳产期末地层压力PRn及该井动态地质储量Gs代入式(17)，可以计算得到该井稳产期末累计产气量Gp。通过计算可得到该井的稳产期Δt为:

式中:Δt为稳产期，天。

4 方法应用实例

以延安气田致密气井Y40井为例。该井射孔层段为山2段，地层压力为20.29 MPa，地层温度为362.89 K，地层有效厚度为12.0 m，储层孔隙度为5.97%，天然气相对密度为0.590 5。

Y40井自2012年6月投产以来，以2×104m3/d生产，油套压力下降稳定，如图1所示。2018年10月，产量大幅下降，油压下降至6.0 MPa之后保持平稳，此时稳产期结束，累计产气4 096×104m3。按照2×104m3/d计算，该井稳产68.3月。

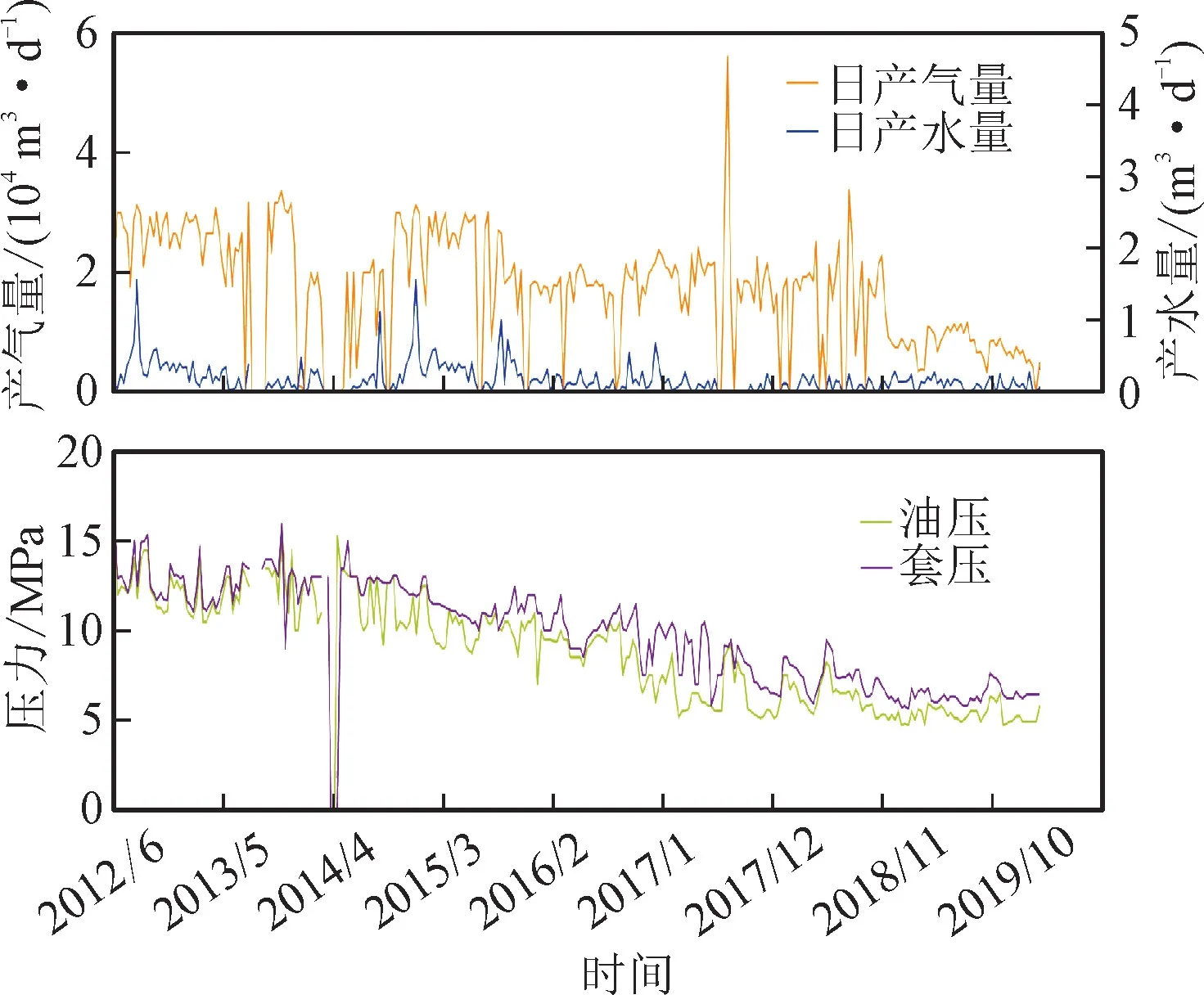
图1 延长气田Y40井产气量及生产压力图Fig.1 Gas production and pressure of well Y40 in Yanchang Gas Field

Y40井山2段应力敏感系数取所在区块平均值0.209 8。利用修正等时试井分析，可计算得到该井初始产能方程的A为5.542 6，B为0.159 8。利用Saphir软件分析修正等时试井压力恢复段数据，获得该井机械表皮系数S为-3.7、非达西流系数D为0.02。修正等时试井延续生产期末，分别为0.017 72，0.948 3，将其与非达西流系数D以及地层温度T一并代入式(16)，计算获得B′为0.772 6，进而得到该井初始地层系数K i*h为4.834 mD·m。

该井以高压集气生产，井口压力p wh不低于5.0 MPa。若该井以2.5×104m3/d，2.0×104m3/d和1.5×104m3/d生产，经过气井垂直管流计算，得到稳产期末井底流压分别为5.96 MPa，5.97 MPa和5.98 MPa(实际计算时，井底流压均取值6.0 MPa)。通过迭代计算获得稳产期末地层压力及稳产期末动态产能方程系数A，B值，如表4所示。采用流动物质平衡法计算该井动态地质储量，结果为1.11×108m3。利用该文方法计算，该井以2.5×104m3/d，2.0×104m3/d，1.5×104m3/d生产时，稳产期分别为41.5月、66.6月、108.9月，如表4所示。

表4 不同方法计算所得Y40井稳产期结果对比表Table 4 Comparison of stable production period calculated by different methods of well Y40

利用气藏模拟软件进行解析解拟合及预测。Y40井采用均质储层、垂直压裂井、有限导流模型。拟合参数:初始地层压力为20.29 MPa，地层渗透率为0.44 mD，裂缝半长为101 m，无因次导流能力为0.044 57，有效厚度为12.0 m，孔隙度为5.97%，含气饱和度为61%，储层压缩系数为0.022 39 MPa-1。Y40井分别采用控制产气量拟合井底流压以及控制井底流压拟合产气量的方法，模型拟合程度良好，如图2所示。使用该拟合结果分别以2.5×104m3/d(预测产量1)、2.0×104m3/d(预测产量2)、1.5×104m3/d(预测产量3)生产，进行稳产期预测，如图3所示，预测结果见表4。

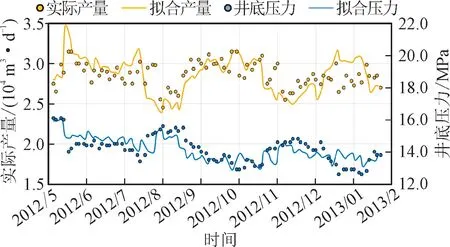
图2 延长气田Y40井产气量及井底压力解析解历史拟合图Fig.2 Numerical simulation of gas production and bottom hole pressure of well Y40

图3 利用Y40井解析解模型模拟不同产量生产的稳产预测图Fig.3 The stable production period of different production rates calculated by using the analytical solution model of well Y40

为3种稳产期预测方法进行编号以便后续描述:①不考虑应力敏感初始产能方程;②考虑应力敏感的动态产能方程;③气藏模拟软件解析解拟合模型预测。

以Y40井实际产量2.0×104m3/d生产时，与该井实际稳产期比较，方法①计算的稳产期过长;方法②计算的稳产期与实际稳产期接近，相对误差在5%以内，表明方法②可靠;方法③计算的稳产期与实际稳产期接近，相对误差在5%以内，表明方法③可靠。

若以2.5×104m3/d，1.5×104m3/d生产时，方法②和方法③计算的稳产期接近。进一步证明了方法②(使用考虑应力敏感的动态产能方程预测气井稳产期)可靠。