裂缝性低渗透油藏窜流规律实验研究

王大为，高振南，李俊飞，葛涛涛，廖 辉

(中海石油(中国)有限公司天津分公司渤海石油研究院，天津 300459)

0 引言

渤海区域内低渗透油藏储量规模较大，尚未形成有效开发，仍处于探索阶段，亟待认清储层渗流规律，加快低渗储量动用[1]。低渗透油藏储层岩石致密，但脆性大，容易产生天然裂缝，形成裂缝性低渗透储层。裂缝性低渗透油藏存在双重介质渗流特征[2-4]，窜流系数是描述该特征的重要参数之一，它反映了基质中的流体向裂缝流动的能力[5-9]，对裂缝性油藏数值模拟结果有较大影响。基质-裂缝间的窜流量计算偏差将引起模拟失真[10-12]。国内外学者对窜流系数开展过诸多研究，但主要是通过试井图版拟合进行求取，室内实验的研究报道较少[13-15]。该文针对渤海低渗目标油田开展室内窜流实验，得出了形状因子和窜流系数等描述裂缝性油藏渗流特征的关键参数，有助于认清渤海低渗透油藏储层渗流规律，提高数值模拟精度和方案研究的可靠性。

1 基质-裂缝窜流实验研究

1.1 实验设备及材料

实验设备主要由抽真空饱和装置、温度和压力监测控制装置、计算机控制系统和流量计量装置等组成，如图1所示。实验设备需满足以下几方面要求:1)自动记录流量和压力数据，精度达到每0.01 s记录一次;2)能够同时计量裂缝和基质中的流体压力值;3)内压测试点左、右各3个，呈对称分布，测试值为40～50 MPa;4)裂缝和基质系统之间至少可建立5 MPa压差。

图1 窜流系数测试实验设备Fig.1 Experimental equipment for measurement of crossflow coefficient

天然岩心两端断面不规整，裂缝形态也较为复杂，难以直接应用于实验。同时，对天然岩心进行切割加工又容易出现岩心破碎的情况，加工难度较大。考虑到上述因素，实验通过对不同配比的灰岩和白云岩颗粒进行胶结，制成具有不同渗透率的全直径人工岩心，应用其研究基质岩块渗透率与窜流系数之间的关系。岩心在室内实验中需要承受较高的压力，选用圆柱状岩心可以更均匀地施加围压;大尺寸岩心加工较为困难，岩心太小则基质-裂缝间的窜流量也较小，造成计量困难。该实验要求岩心直径(100±5)mm，岩心长度最大150 mm。实验选取5块全直径岩心，利用全直径岩心夹持器和室内窜流实验测试装置测试不同基质渗透率条件下窜流系数。实验用岩心的基质渗透率采用液测法测得，岩心的基本参数如表1所示。

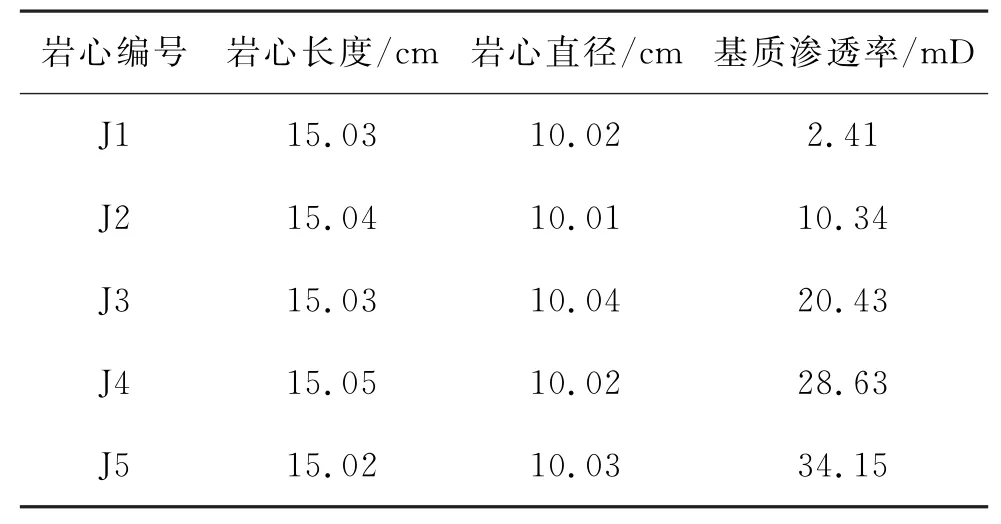
表1 岩心基本参数表Table 1 Basic parameters of core

根据实验区块地层水配方进行实验用水配样:在30℃下，通过黏度测试仪测试实验用水的黏度为1 mPa·s，利用密度仪测试出实验用水的密度为0.992 g/cm，总矿化度为7 726 mg/L，如表2所示。

表2 实验用水水样无机盐含量Table 2 Contents of inorganic salts in experimental water samples mg/L

1.2 实验原理

窜流实验设计主要是基于窜流微分方程和物质平衡原理，采用高精度压力传感器和电子天平实现准确计量，完成实验设计。根据Warren-Root的理论可知，流体在基质-裂缝之间窜流时，有:

式中:λ为窜流系数，无因次;α为形状因子;A为岩心横截面积，m2;K m为基质的渗透率，mD;K f为裂缝的渗透率，mD。

在确定了基质渗透率K m、裂缝渗透率K f、岩心横截面积A，以及求取了形状因子α之后，就可以根据式(1)求出窜流系数λ。

1.3 实验步骤

1)将实验岩心装入全直径岩心夹持器中，设定好围压值、回压值以及微计量泵的泵入流量;

2)通过微计量泵向岩心内泵入实验用水;

3)开启回压增压手阀给岩心回压，使岩心各处压力平衡;

4)待压力稳定后停止微计量泵供液;

5)打开回压阀，瞬间降低回压，使岩心内基质-裂缝间发生窜流;

6)回压阀开启短时间后立即关闭，通过窜流实验软件观测岩心夹持器内各处压力传感器数值，待入口、出口及岩心内部各压力值稳定后，将所记录数据导出备用;

7)根据测得的基质和裂缝压力数据，计算出形状因子α和窜流系数λ。

1.4 实验结果

在几何形态相同、定围压的情况下选择基质渗透率不同的岩心进行实验。实验所用岩心的基本参数和实验测试的结果如表3所示。

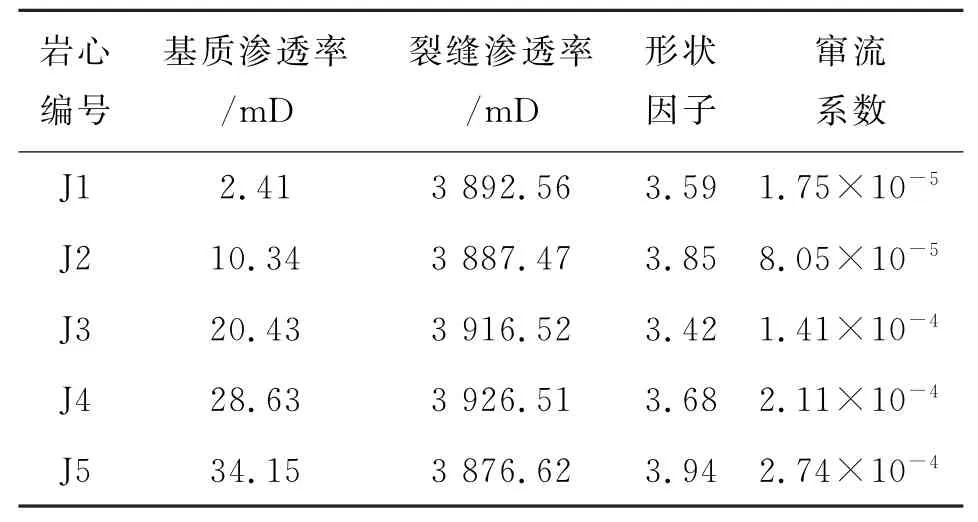
表3 不同基质渗透率的计算结果Table 3 Calculation results of different matrix permeability

实验中5块全直径岩心的基质渗透率为2.41～34.15 mD，差异相对较大;裂缝渗透率为3 876.62～3 926.51 mD，较为接近。实验测定的形状因子为3.42～3.94，可见在全直径岩心网格尺寸相同、几何形态相同、定围压的情况下，各岩心的裂缝渗透率和形状因子较为相近。

在岩心横截面积、裂缝渗透率和形状因子接近的情况下，窜流系数的值主要受基质渗透率差异的影响。根据实验测定的形状因子，再由式(1)可计算得到窜流系数为1.75×10-5～2.74×10-4，而在油藏规模条件下，窜流系数λ一般为10-10～10-4[16]，该实验所测得的λ为10-5～10-4，符合一般规律，同时也验证了实验装置的可靠性。

2 结果分析与讨论

2.1 窜流系数与基质渗透率关系

为了寻找储层窜流规律，可以根据上述实验结果，做出窜流系数随不同基质渗透率的变化曲线，如图2所示。

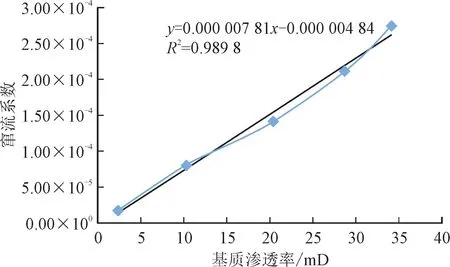
图2 窜流系数随不同基质渗透率的变化曲线Fig 2 Variation curve of crossflow coefficient with different matrix permeability

岩心的窜流系数与基质渗透率基本成线性关系，随着基质渗透率的增大，窜流系数线性增大，从1.75×10-5增加到2.74×10-4，增幅较大。形状因子的数值取决于基质岩块的大小和正交裂缝的组数，储层中如果被分割的基质岩块越小，则裂缝的密度相应就越大，得到的形状因子也就越大。窜流系数随着形状因子和基质渗透率的增大而增大，所以基质岩块越小、基质渗透率越大，测得的窜流系数就越大，表明基质中流体向裂缝的窜流能力越强。岩心样品J1～J5的裂缝渗透率和形状因子较为接近，而基质渗透率逐渐增大，因此窜流能力也逐渐增强。

通过线性回归，得到窜流系数与基质渗透率的关系式为:

可以应用上述关系式预测目标油田不同基质渗透率下的窜流系数，为油藏数值模拟和开发方案编制奠定基础。

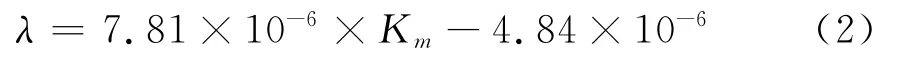
2.2 应用窜流系数预测压裂井产能

结合上述窜流实验结果，可以预测压裂井初期产能，对渤海低渗目标油田储层Ⅰ和Ⅱ油组进行压裂效果评价。由Ⅰ和Ⅱ油组的基质平均渗透率，结合基质渗透率和窜流系数相关性回归直线的结果，可以分别求出各自的窜流系数，再反求形状因子，继而可求得单位体积、单位时间的窜流量。根据不同裂缝的裂缝半长和储层的厚度可以得到发生窜流的岩块的体积，结合上面求得的单位体积、单位时间的窜流量，便可算出单井的产量。结果和各项参数如表4所示。

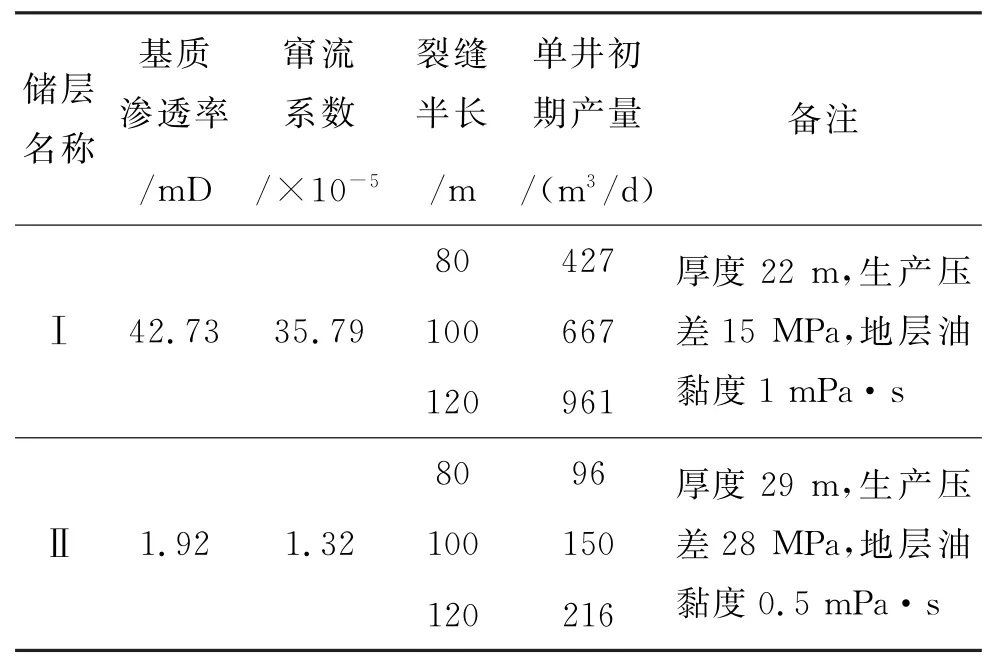
表4 储层压裂产能预测Table 4 Reservoir fracturing productivity prediction

从表4可知，Ⅰ油组储层基质平均渗透率为42.73 mD，而Ⅱ油组储层基质平均渗透率仅为1.92 mD，远小于Ⅰ油组。由式(2)可得，Ⅰ油组储层窜流系数为35.79×10-5，而Ⅱ油组储层窜流系数仅为1.32×10-5，也远小于Ⅰ油组。结合Ⅰ油组储层厚度22 m、地层原油黏度1 mPa·s、生产压差15 MPa，Ⅱ油组储层厚度29 m、地层原油黏度0.5 mPa·s、生产压差28 MPa，便可得到裂缝性低渗透油藏不同裂缝半长(80 m，100 m，120 m)时对应的单井初期产油量。裂缝半长越长，对应的单井初期产量越高。当裂缝半长由80 m增大到120 m时，Ⅰ油组储层单井初期产量由427 m3/d增大到961 m3/d，Ⅱ油组储层单井初期产量由96 m3/d增大到216 m3/d，由于储层基质渗透率和窜流系数的差异，Ⅱ油组单井初期产量远小于Ⅰ油组。

3 结论

1)通过室内实验研究了裂缝性低渗透油藏中基质和裂缝之间的窜流特征，测得了不同岩心的形状因子和窜流系数。测试得到的形状因子数值为3.42～3.94，较为接近;不同岩心的窜流系数随着基质渗透率的增加变化幅度较大，为1.75×10-5～2.74×10-4。回归得到的基质渗透率与窜流系数关系式可以用于预测目标油田的窜流系数。

2)结合窜流实验结果，对渤海目标油田低渗储层进行了压裂效果评价。根据不同裂缝的裂缝半长和储层厚度，以及单位体积、单位时间内的流体窜流量，计算出了不同储层的单井产量。由于Ⅰ油组储层基质平均渗透率大于Ⅱ油组，因此根据统计规律计算的窜流系数也相对较大，不同裂缝半长的单井初期产能为427～961 m3/d，也远大于Ⅱ油组的96～216 m3/d。