隐形矫治磨牙远移的三维有限元分析

雷 鹤，高 冲，吴冬雪，魏亚珊，刘美杰，邓春妮，陈 曦

磨牙远移技术是通过增加牙弓长度开拓间隙，解除牙列轻中度拥挤、前突，改善磨牙安氏Ⅱ类错牙合的常用临床手段之一。过去，临床上常用头帽、口外弓、J钩等依赖型矫治器或钟摆式矫治器、改良式钟摆式矫治器等非依赖型矫治器，进行磨牙远移[1-2]，但以上矫治器结构较复杂，佩戴舒适度、美观性欠佳，增加了患者诊疗过程中的负担。近年来，隐形矫治技术的出现和发展，为磨牙远移提供了新的思路，使其重新成为临床研究热点之一[3-5]。现有研究结果表明隐形矫治进行磨牙远移较以往装置更加简单、高效[4-5]。但这些研究样本量较小且大多为观察性研究，结果具有一定的局限性。目前尚不能检索到大样本高质量的临床随机对照研究或此方面生物力学研究，隐形矫治技术磨牙远移的牙齿移动方式及牙周膜受力情况不甚明确。

有限元法(finite element method，FEM)是一种求解连续介质力学问题的理论应力分析方法，目前已经成为口腔正畸学生物力学研究常用的分析工具之一[6-14]。有学者研究表明，使用优化附件可以避免尖牙远移过程中不希望的倾斜移动[15]。目前未见使用隐形矫治器进行磨牙远移的相关生物力学研究。

磨牙远移的过程中不可避免会有支抗丧失[16-19]。有医生认为用隐形矫治器不配合Ⅱ类牵引不可能完成Ⅱ类患者的矫治[18]。但Simon等[5]研究表明，隐形矫治全程不进行任何牵引增强支抗就可达到87%磨牙远移的实现率。目前为止，使用Ⅱ类牵引增强支抗的必要性及足够抵抗前牙支抗丧失又不损伤牙周膜健康的适宜牵引力值未见相关研究。

本研究拟通过建立隐形矫治器磨牙远移的三维有限元模型，模拟佩戴隐形矫治器后牙齿与矫治器之间的相互作用，使用有限元分析软件开展非线性力学分析，预测矫治器佩戴后初始状态下牙齿、牙周膜及矫治器本身的位移或应力的大小及分布，探索牙齿移动方式、牙周膜应力大小及分布、牙套形变特征及Ⅱ类牵引增强支抗的必要性及适宜力值，为临床医生制定隐形矫治方案及复诊监控提供依据与指导。

1 资料与方法

1.1 建立有限元模型

1.1.1 数据获取 本研究纳入标准为：年龄大于18岁；轻中度拥挤；无或已拔除上颌第三磨牙，上颌磨牙后间隙足够；单侧或双侧后牙远中关系；骨性Ⅰ类或Ⅱ类错牙合；均角或低角；非拔牙矫治设计；拟使用隐形矫治技术矫正，分步推磨牙向后；推磨牙向后量小于等于4 mm。严格按照以上纳入标准，选取2019年2月就诊于西安交通大学第一附属医院口腔科的一位患者作为研究对象(女，24岁，上牙列拥挤度1 mm，已拔除上颌第三磨牙，双侧磨牙远中关系，骨性Ⅰ类，均角，拟使用隐形矫治“V pattern”分步远移磨牙4 mm)。拍摄CBCT并导出患者DICOM格式文件。

1.1.2 建立CAD模型 使用Mimics(Materialise公司，比利时)软件导入上述获得的DICOM数据，调整阈值范围，在矢状向、冠状向及垂直向的所有层面影像中细化、分割、修补、3D计算，获得初步的三维模型(图1A)。将所得到的模型以.STL格式保存并导入UG Unigraphics NX(德国Siemens PLM Software公司)进行拟合表面实体化。拉伸及布尔运算(减法)，将牙根表面均匀拉伸0.2 mm得到牙周膜模型(图1B)。得到模拟矫治前的牙列-牙周膜-牙槽骨模型M。考虑到矫治器的滞后性，左右两侧上颌第二磨牙向远中移动0.3 mm，其余牙不动，得到模拟矫治过程的牙颌模型M′。沿牙冠外表面向外扩展0.75 mm，修剪矫治器龈缘去除初始模型M′，使用拉伸和布尔运算建立矫治器的模型MA(图1C)。

A：牙齿-牙周膜模型；B：矫治器模型；C：佩戴矫治器后的牙列模型

1.2 网格划分

将上述模型划分为由有限个四面体十节点单元为基本单位构成的整体，模型共划分为125 999单元和218 468节点，各部分具体划分的单元及结点数见表1。

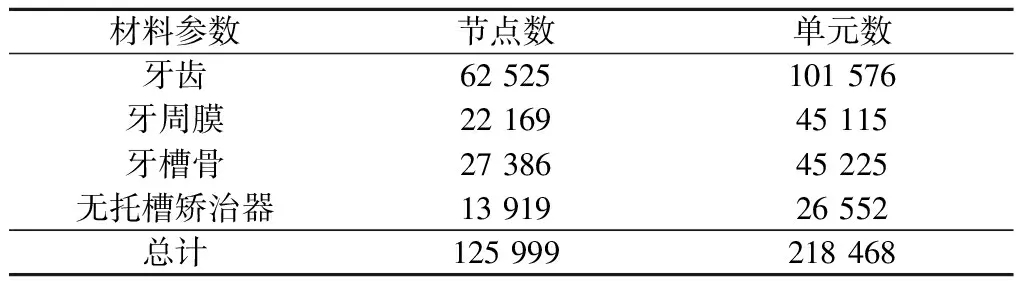
表1 有限元模型各部分节点数和单元数

1.3 材料属性定义

牙齿、牙槽骨、牙周膜、隐形矫治器的弹性模量及泊松比具体参数见表2。所有材料在受力状态下均为小形变[13]。设定四种材料均为均质、各向同性的线弹性体[13,20]。

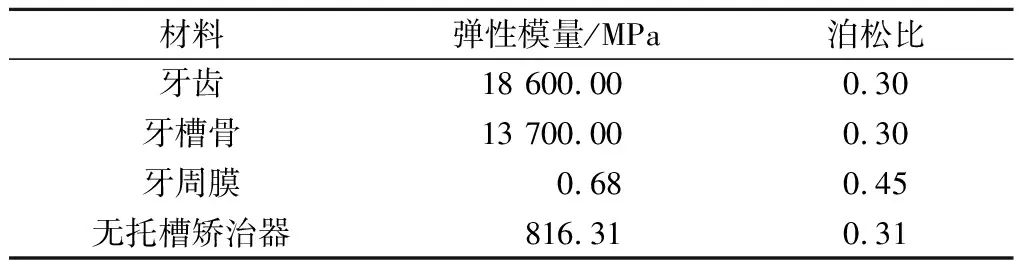
表2 材料属性

1.4 边界约束

设定牙槽骨外周为“固定”约束。牙根与牙周膜、牙周膜与牙槽骨之间为“粘接”接触，受力后位移相同应力不同，不发生相对滑动。隐形矫治器内表面与各牙冠外表面定义为“柔性”接触关系，计算机可以按照力学计算原则计算出两个可变形接触体实际接触状态。初始状态下不设计隐形矫治器的任何约束或载荷条件。

1.5 模拟磨牙远移及牵引

初始模型M和矫治器模型MA以M′为标准进行装配，模拟矫治器的佩戴(图1C)。在左右两侧牙套上尖牙唇面颈缘中点位置施加向下向后与水平向25.75°夹角方向的力。依次施加0 g(无Ⅱ类牵引)，100、150、200、250、300 g载荷。

2 结 果

2.1 牙齿移动方式

拟矫治牙(第二磨牙)表现为远中倾斜的位移趋势，根尖部则表现出相反的位移趋势。最大位移量5.291 7×10-7m，位于近中舌尖处，颊侧位移最小量位于根分叉处，腭侧位移最小量位于根尖1/3处。牙齿旋转轴由颊侧根分叉处斜向腭侧根尖处，腭侧移动量大于颊侧。此外，第二磨牙在垂直向上表现为伸长的移动趋势，水平向上表现为近中舌倾、远中颊倾的趋势(图2)。

支抗牙则表现为近中移动的趋势，从第一磨牙、第二前磨牙、第一前磨牙、尖牙、侧切牙及中切牙牙冠中心的位移量依次减小，位移量与支抗牙的距离成反比(图2)。图中红色、黄色、绿色表示较大位移量，蓝色表示较小位移量，图中可见第二磨牙、第一磨牙有较明显的位移，第二前磨牙、第一前磨牙及尖牙仅牙冠处有较小的位移，侧切牙、中切牙处基本无位移量。

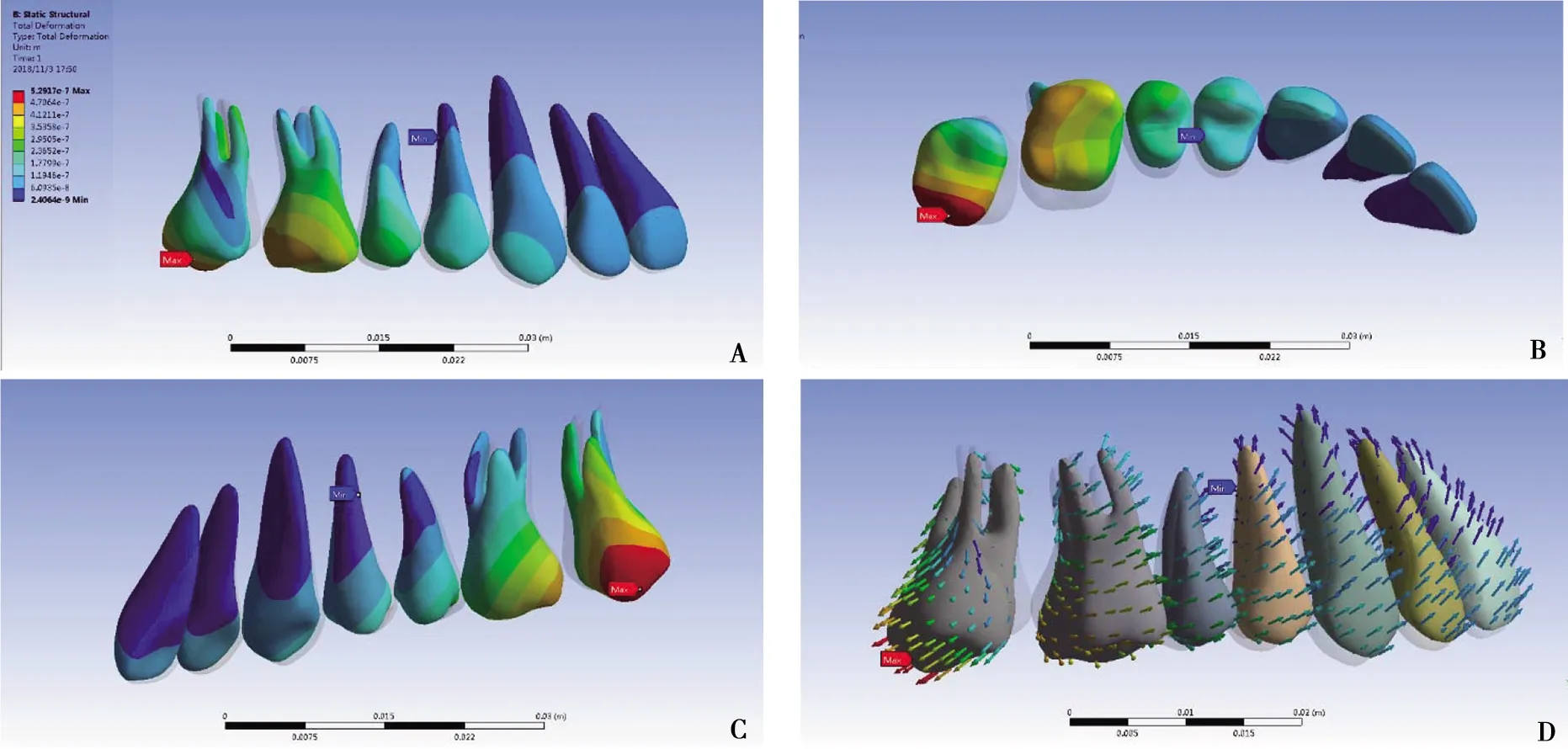
A：颊面观；B：牙合面观；C：舌面观；D：移动趋势

2.2 牙周膜应力分布

磨牙远移中的牙周膜应力主要集中在第一、第二磨牙上，呈现越靠近颈缘应力越大的趋势，距离矫治牙越远受力约小。牙周膜等效应力最大为3.27×103MPa，位于第二磨牙牙周膜近中颈缘，最小为2.86 MPa位于中切牙舌侧牙周膜根上1/3的位置，如图3。

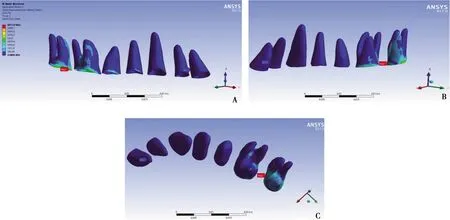
A：颊面观；B：舌面观；C：根面观

2.3 矫治器形变

矫治器本身为非均匀受力，第二磨牙处(拟矫治牙位)出现应力集中现象，位移峰值5.833 2×10-7m,位于第二磨牙远中舌侧位置，小于材料的弹性极限和拉伸极限强度。最小等效应力为2.792 5×10-8MPa，位于中切牙舌侧颈缘。其余牙对应的矫治器形变量随着与矫治牙的距离增加而减少。其中前牙段矫治器发生唇向、根向移位；磨牙段矫治器发生冠方、颊侧移位，如图4。

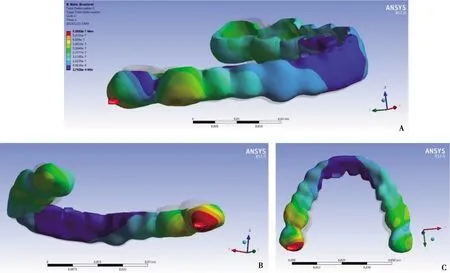
A：颊面观；B：舌面观；C：牙合面观

2.4 适宜支抗力值的探讨

无施加Ⅱ类牵引时前牙受到磨牙远移的反作用力被唇倾、压低。施加Ⅱ类牵引后所有组均表现为前牙内收伴伸长，如图5，且牵引力值越大前牙内收的量越大。牙周膜受到的等效应力见表3。

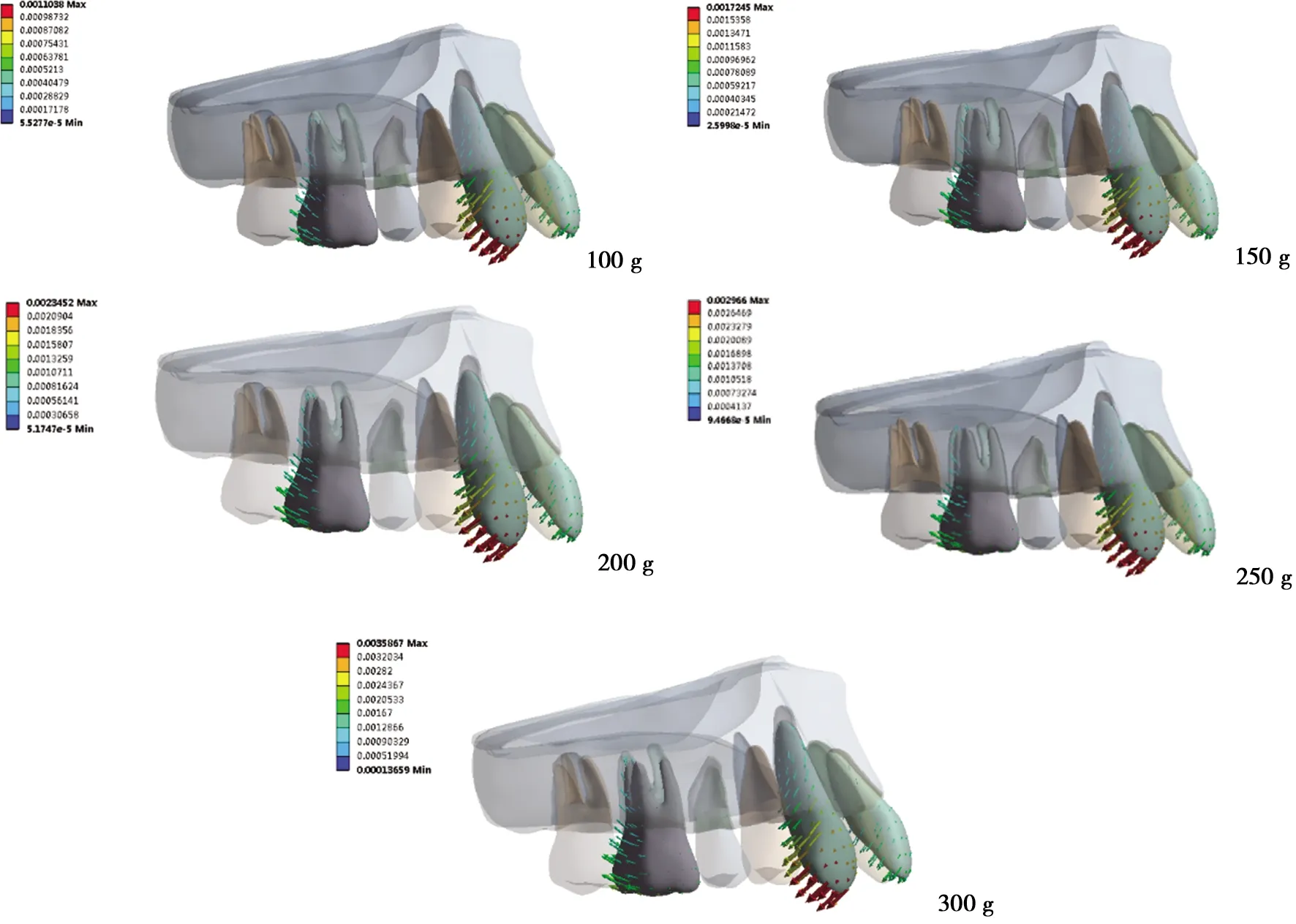
图5 Ⅱ类牵引下的牙齿移动趋势

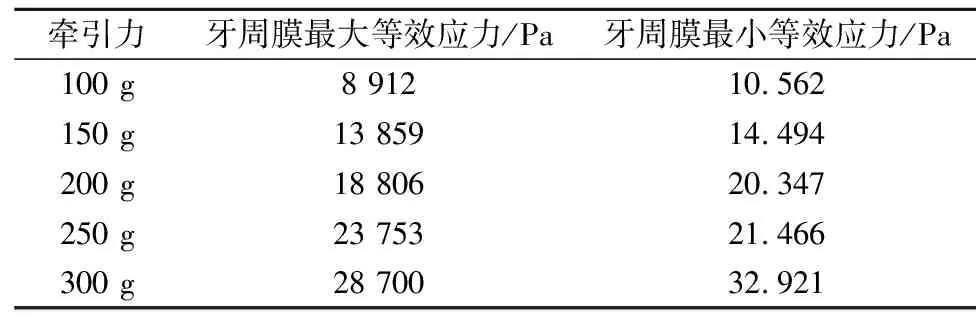
表3 Ⅱ类牵引牙周膜等效应力大小

3 讨 论

建模是否准确是有限元分析结果是否可靠的基础和关键。以往研究多以单个牙齿为研究对象[17,21], 没有建立完整的上颌牙列及矫治器的模型，未能反映隐形矫治器这个连续的弹性整体的生物力学特征，忽略了牙齿之间及牙齿与牙套之间的相互作用对矫治结果的影响，临床意义有限。本研究建立了完整的牙列、牙槽骨、牙周膜及隐形矫治器模型，增加了工作量和难度，但在建模完整性及准确性上较以往研究有了较大的突破，尽可能还原临床现象，为准确揭示磨牙远移的生物力学特征打下了基础。

由于磨牙牙根的复杂性、加力情况的差异、阻抗中心的不同等，目前临床上常用的磨牙远移矫治器是否能实现牙齿的整体移动有争议。有学者研究发现使用隐适美可以实现例如磨牙远移、切牙转矩、前磨牙去扭转等整体移动[5]。Rossini等[22]也认为隐形矫治器可以有效实现磨牙1.5 mm的整体远移。然而，大多数学者则认为隐形矫治器近远中向移动牙齿的效果是倾斜移动[22-24]。Ravera等[4]对隐适美推磨牙向后病例分析发现第二磨牙、第一磨牙分别倾斜2.64°、1.64°，但差异无统计学意义。本研究结果显示第二磨牙并非整体移动，而是伴随有远中倾斜、伸长，远中旋转、舌侧倾斜，与以往研究结果一致。这提示我们在方案设计阶段对拟矫治牙进行特殊的设计。

本研究不涉及附件的应用，隐形矫治器靠佩戴后矫治器的形变产生的回弹力对牙齿起到矫治的作用。现有研究结果对附件在磨牙远移过程中的作用有不同的观点。有学者用三维有限元法研究尖牙的远中移动模式，发现辅助使用一对优化附件可以产生尖牙整体运动的力系[15]，但其仅创建了尖牙及其对应的部分牙槽骨及局部牙套，其结论有待进一步深入研究。另外，有临床研究结果显示，使用附件和未使用附件进行上颌磨牙远移，矫治结果无显著差异[5]。综上所述，附件可能的确对牙套的固位及牙齿移动的结果有一定的影响，但推磨牙过程不需要特定的附件且临床上其他牙齿附件多为个性化设计，随意增加附件会限制本研究的适用性。附件对磨牙远移结果的影响仍需进一步深入探讨。

磨牙远移过程中的垂直向变化一直是临床医生关注的问题：一般认为，由于楔形效应，磨牙远移会导致垂直高度的增加。本研究结果表明远移的磨牙有远中倾斜、颊倾与伸长的移动趋势。但以往临床研究与理论研究结论不同：Gianelly等[24]发现磨牙远移前后高、中、低角患者的面下高度均无显著变化。Caprioglio 等[25]对76例使用摆式矫治器的患者进行7年的随访分析得出：磨牙远移和固定矫正阶段期间面高增加，但是在保持阶段恢复正常。此外有学者认为前面下高度的轻微增加与磨牙倾斜有关[26]。Serena等[4]使用Invisalign磨牙远移后第二磨牙、第一磨牙分别压低0.51 mm、0.31 mm，差异无统计学意义。这种差异可能由于临床研究样本量普遍较小，其代表性有待考察；且隐形矫治临床上可见部分患者在矫治过程中后牙开牙合，可能由于佩戴过程中咬合力的作用，这点在理论研究中无法涉及；也可能方案中牙齿并非单一方向的移动，在最优牙齿移动路径中除了磨牙向远中还有部分压低。目前未见高质量、大样本的临床研究，此部分仍需进行深入探讨。

过大的正畸力会压闭压力侧的牙周膜血管，发生潜掘性吸收，不利于正畸牙的移动。Lee[27]、卢海平[28]等研究认为牙周膜可承受的等效应力值最大不应超过2.6×10-2MPa，否则易引起牙周组织不可逆改变甚至导致牙周膜坏死。本研究中无Ⅱ类牵引第二磨牙远移0.3 mm 及100 g、150 g、200 g、250 gⅡ类牵引磨牙远移0.3 mm组中所产生的牙周膜等效应力均小于该值，位于牙周组织可承受范围之内且无牙根吸收风险。但300 gⅡ类牵引组牙周膜应力过大超出牙周膜安全范围，这提示我们尽量避免使用过大的牵引力。

本研究也存在一些局限性，如何完全准确仿真牙齿移动过程中的生物力学规律及时间因素在牙齿移动中的影响等尚不能探索。本实验的局限性也是有限元分析方法技术的局限性，未来随着计算机技术的发展及牙齿移动机制的深入研究，一个仿真度更高的各向异性、非均质、非线弹性有限元模型建立及应力作用下的牙槽骨改建将成为未来发展的趋势。

4 结 论

本研究通过三维有限元分析表明，使用无托槽矫治技术远移磨牙时，磨牙移动并非完全的整体移动，前牙也伴随一定程度的支抗丧失，应辅助拟移动牙适当的压低、扩弓或其他特殊设计，支抗牙需要进行必要的支抗控制。

使用Ⅱ类牵引增加磨牙远移过程中的支抗时，100 g的Ⅱ类牵引足以抵抗推磨牙过程中的前牙支抗丧失，300 g牵引力作用下的牙周膜受力过大，尽量避免使用。