基于MLP的连续梁桥损伤识别

王平波 谢祥辉 单德山

【摘要】多层感知器（Multi-Layer Perceptron，MLP）在模式识别领域有着广泛的应用，为探索其在桥梁损伤识别中的应用，文章以两跨连续梁桥为研究对象，提出了基于多层感知器的连续梁桥损伤识别方法。采用梁截面的曲率模态作为损伤指标，以各截面的曲率模态作为模式输入，不同位置的损伤状态作为模式输出，建立损伤指标与损伤模式之间的映射关系。研究结果表明：所提方法能够准确识别连续梁桥的损伤位置，并且在添加一定程度的噪声之后，仍能保持良好的识别效果。

【关键词】连续梁桥; 多层感知器; 神经网络; 损伤识别; 曲率模态

【中国分类号】U441+4【文獻标志码】A

桥梁结构在运营过程中，会不可避免地因结构老化、疲劳和地震等因素而发生损伤。因此，及时准确地损伤识别，对提高桥梁结构的可靠性、安全性和耐久性都具有很重要的现实意义[1]。目前，桥梁损伤识别研究正朝着深度学习方向发展[2]，研究表明，深度学习中的多层感知器网络具有良好的模式分类与泛化能力，在桥梁损伤识别领域应用中有较大的潜力。为探索多层感知器网络在桥梁损伤识别中的应用，以两跨连续梁桥为研究对象，提出了基于多层感知器的连续梁桥损伤识别方法。

1 多层感知器网络

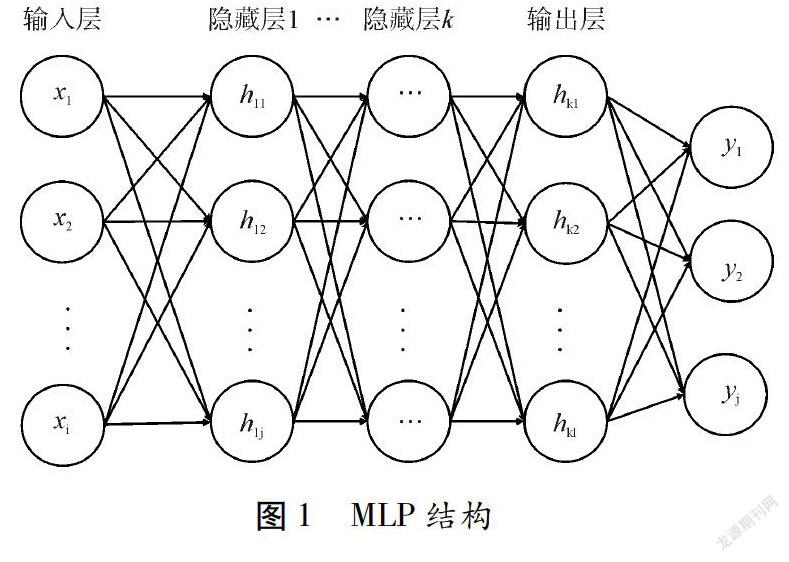
多层感知器（Multi-Layer Perceptron，MLP）是一种前向结构的人工神经网络，目前广泛应用于图像处理、模式识别、优化计算、函数逼近等领域[4]。MLP由1个输入层、多个隐藏层和1个输出层组成，每层由多个神经元节点组成，其网络结构如图 1所示。

2 基于MLP的桥梁损伤识别

基于MLP的桥梁损伤识别包含确定损伤指标、构建样本库、网络的监督训练和测试3个步骤，具体流程见图2。

2.1 损伤指标的选取

损伤指标的确定应当考虑损伤指标对结构损伤的敏感性，能够真实反映结构损伤状态。

对于连续梁来说，任意梁截面的曲率φ可以表示为φ=M/EI，式中：M为作用于梁截面的弯矩，EI为梁截面的抗弯刚度。由此可见，梁截面刚度的下降会引起截面曲率的改变，可以用曲率模态来识别梁结构的损伤。同时，根据文献[6]的研究，曲率模态对损伤识别的效果较好，故本文采用曲率模态作为连续梁损伤识别的指标。

2.2 模型的建立

将各个截面的曲率模态依次连接，作为模式输入，以不同损伤类别作为模式输出，构建了监督训练样本库。以向量的形式可以表示为Si=x1，x2，…xn，yi，其中Si表示样本库中的第i个样本，x1，x2，…xn表示该样本中有n维损伤特征，yi表示该样本所属类别。

2.3 MLP网络的训练

2.3.1 激活函数的选取

选取激活函数的目的在于引入非线性因素，以增强整个网络的表征能力，常用的激活函数有Sigmoid函数、Tanh函数和ReLU函数。

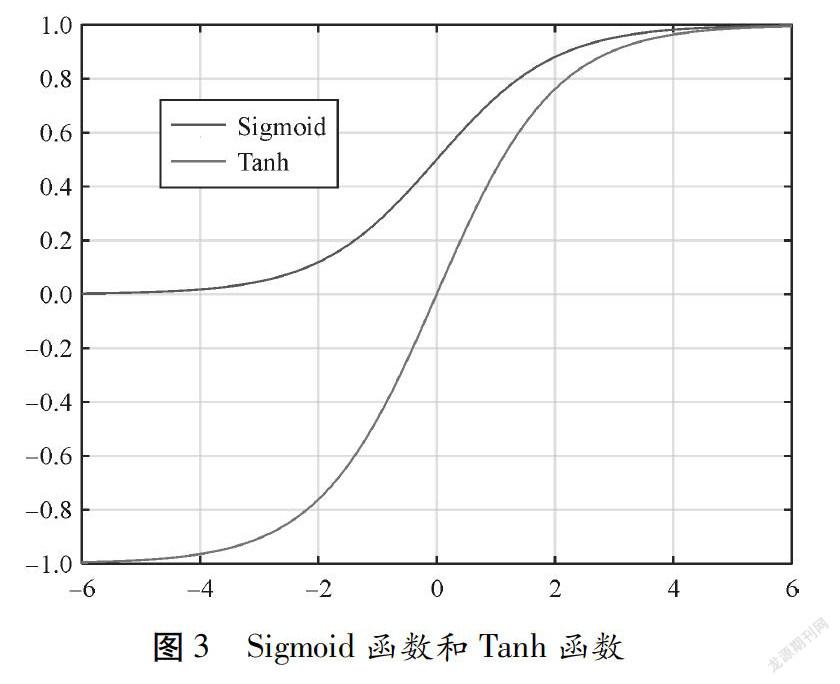
Sigmoid函数的表达式如式（1）所示，映射区间为（0，1），其函数图形如图 3所示。

Tanh函数的表达式如式（2）所示，映射区间为（-1，1），其函数图形如图 3所示。

由式（2）可见，Tanh函数可以看做是Sigmoid函数的线形变换，二者具有一定的相似性。Sigmoid函数和Tanh函数有一个很大的缺点，那就是他们的导数值很小，且当输入数据很大或者很小的时候，其倒数值都接近于0。这就意味着，这类激活函数很容易产生梯度消失现象。

因此，如何防止深度神经网络陷入梯度消失的境地，或说如何提升网络的训练效率，一直都是深度学习非常热门的研究课题[3]。目前，在多层感知器中，常用的激活函数是ReLU函数。ReLU函数的表达式非常简单，即fx=max （x，0）。也就是说，当x>0时，输出x;当x≤0时，输出为0。相比于Sigmoid函数和Tanh函数，ReLU函数克服了梯度消失问题[4]。故本文选取ReLU函数作为激活函数。

2.3.2 损失函数的选取

在深度学习中，对于给定的输入x，网络预测输出y-和目标输出y可能不一致。于是，需要定义一个损失函数，来描述这两者之间的“落差”程度[3]。

常用的损失函数有交叉熵损失函数（Cross Entropy Loss）、均方差损失函数（Mean Squared Error）和边缘损失函数（Margin Loss）。

对于多分类问题，最常用的损失函数就是交叉熵损失函数（Cross-Entropy）。交叉熵损失函数的表达式为CEp，q=-∑pxlogq（x），其中p和q分别代表真实概率分布和预测概率分布，当交叉熵损失越小时，说明真实概率与预测概率相差越小，本文采用CEL作为损失函数。

2.3.3 分类器的选取

目前，在分类问题中，常用的分类器有支持向量机（Support Vector Machines，SVM）和Softmax函数。但是基本形式的支持向量机只能处理两分类问题，对于多分类问题则需要重新构造多分类网络结构。Softmax函数可视为逻辑回归在多分类问题上的推广[3]。Softmax函数的表达式如式（3）所示。

对于一个k维向量z1，z2，…zk，经过Softmax函数归一化处理后，可以输出一个长度为k的向量p1，p，…pk，而且∑kj=1pj=1。也就是说，对于输入向量z，经Softmax函数处理后，输出的是不同类别的概率分布。故本文采用Softmax函数作为分类函数。

2.3.4 网络的训练

网络的训练过程，也就是网络参数的寻优过程，最基本的寻优算法是随机梯度下降法（Stochastic Gradient Descent，SGD）。但是SGD在训练过程中无法调整学习率，收敛速度较慢。为此，很多学者提出了相应的改进算法，其中Adam算法应用最为广泛[8]。因此，本文采用Adam算法作为网络的训练方法。

3 有限元模型验证

3.1 模型概况

采用Midas软件建立了两跨连续梁桥有限元模型，截面为1 m×1 m的矩形，长度为12 m+12 m，共24个单元，每个单元长度为1 m。该模型桥采用钢材，其弹性模量为E=2.06×108 kN/m2，考虑到结构损伤主要体现为结构刚度的下降，为简化计算，不考虑截面尺寸的变化，以材料弹性模量的下降来模拟损伤。

3.2 损伤模式分类

本文设定的损伤工况有单处损伤、两处损伤和三处损伤这三种情况，损伤模式类别则由不同的损伤位置来确定，分别设置0～8这9种不同的工况。具体的损伤单元和损伤程度见所示。中的损伤单元，分别发生10 %，20 %，30 %，40 %和50 %的损伤，就构成了本文训练用的监督训练样本库（表1）。

中X0为未加噪声之前的样本，X为添加噪声之后的样本，ε为噪声水平，σ为标准高斯随机数（均值为0，标准差为1）。

添加噪声后识别结果如表 3所示，可见，在添加了20 %的噪声后，发生了一个误判，即将工况7误识别成了工况4，其余均识别正确，准确率为88.9 %。测试结果表明，所提的方法的抗噪性能良好。

4 结论

本文通过对两跨连续梁进行了损伤识别，并测试了基于MLP 的损伤识别方法的抗噪性能，主要结论如下：

（1）本文提出的基于MLP 的损伤识别方法，识别效果很好，在添加了20 %的噪声后，仍能保持88.9 %的识别准确率，具有较好地抗噪性能。

（2）由于本文针对的是简单的连续梁桥，获得的样本数量有限，样本库容量偏小，在其他复杂桥梁上的应用效果还需要进行深入研究。表3 添加20 %噪声后的识别结果

参考文献

[1] 朱宏平，余璟，张俊兵.结构损伤动力检测与健康监测研究现状与展望[J].工程力学，2011，28（2）：1-11+17.

[2] 单德山，李乔，付春雨. 智能桥梁健康监测与损伤评估[M]. 人民交通出版社， 2010.

[3] 张玉宏. 深度学习之美[M]. 中国工信出版社， 2018.

[4] Li Y， Yuan Y. Convergence Analysis of Two-layer Neural Networks with ReLU Activation[C]. neural information processing systems， 2017： 597-607.

[5] 王格格，郭濤，李贵洋.多层感知器深度卷积生成对抗网络[J].计算机科学，2019，46（9）：243-249.

[6] 李国强，梁远森.振型曲率在板类结构动力检测中的应用[J].振动、测试与诊断，2004（2）：27-32+75.

[7] 谢祥辉. 基于深度学习理论的桥梁损伤识别研究[D].成都：西南交通大学，2018.

[8] Goodfellow I， Vinyals O， Saxe A M， et al. Qualitatively characterizing neural network optimization problems[J]. arXiv： Neural and Evolutionary Computing， 2014.