陆地风电机组重力基础旋转刚度计算

韩莹 李继祥 王东元

【摘要】文章比较了国内外规范中风电重力基础旋转刚度的简化计算方法，结合实际工程项目，利用规范近似法和Plaxis3D有限元软件计算了基础旋转刚度并进行了比较，并对有关参数进行了分析研究。结论表明：中外规范中基础置于基岩岩顶工况同有限元计算结果非常接近，对动态旋转刚度，规范法计算结果均小于有限元计算结果，但对静态旋转刚度，规范法的计算结果却偏大;在地基土质刚度较大时，归一化计算刚度和归一化剪切波/小应变剪切模量呈现近似线性对应关系;在地基土质变软情况下，归一化计算刚度的变化趋于平缓。

【关键词】风电基础; 旋转刚度; 剪切模量; 小应变硬化模型

【中国分类号】TU470【文献标志码】A

我国陆地、近海可利用的风力资源均达世界前列，但对风电的规模利用起步较晚，对风电基础的设计一般是根据风机基础的受力条件、现场实际地质条件、可行性等多方面因素进行比选才能最终确定基础形式[1]。为有统一参考，减少技术分歧，弥补有关空白，2008年水利水电规划研究总院颁布FD003-2007《风电机组地基基础设计规定》[2]，结束了直接引用国外设计图集、在项目具体实施中反复修改的现象。之后有关人士进行了相关工作，庞作会等[3]根据指出风机基础需要进行基础底面脱开地基面积验算、基础钢筋和混凝土的抗疲劳验算以及基础动刚度验算;章子华等[4]提出基础变形和抗倾覆能力是基础设计的控制指标;许新勇等[5]基于ANSYS平台考虑接触非线性探讨了基础结构的受力特性。2016年，国家能源局颁布了水利水电规划研究总院主编的《陆上风电场风电机组地基基础设计规范》（征求意见稿）[6]，更进一步地推动了我国风机机组基础设计的发展和进步。

尽管如此，还是存在国内外规范不统一、设计人员对设计标准要求理解不深刻不全面的现象。针对风电基础工程设计的具体要求还停留在传统建筑结构基础工程层面，而结合风电机组风力循环荷载及弯矩较大等鲜明特征下的特殊要求比如旋转刚度，国内却鲜有研究报道。本文比较了国内外规范风电重力基础旋转刚度简化计算以及有限元计算方法，对利用简化计算模型和利用Plaxis 3D有限元分析模型计算的旋转刚度进行了比较，对有关参数进行了分析研究。

1 陆地风电重力基础旋转刚度计算模型

风电机组是将风力转为电能的一种设施，整个系统包括叶片、风机、塔架到基础，其受力如图1所示。风机不同工作状态下受力区别明显，国际电工委员会IEC [7]根据风机的工作状况划分设计荷载工况，如正常生产、正常生产但有局部问题、启动、关机等。风机制造商根据IEC有关规定，会在其技术文件中提供有关基础设计荷载和技术要求，见表1。风机基礎承受的弯矩荷载非常大，扩展基础要用混凝土和基础上部回填土的重量抵抗风力荷载的倾覆弯矩，因此这类基础也称为重力基础。重力基础不仅要满足传统基础工程分析设计的各种要求，且限制基础底部压力为零区域面积，并对旋转刚度要求较高。

动力基础的设计存在两类建模方法，一是质量-阻尼-弹性理论体系，另外一种是弹性半空间体系[8]，具体计算基本上分为两大类，规范近似法和数值分析法[9]，其中国内规范NB/T 10311-2019《陆上风电场工程风电机组基础设计规范》规定扩展基础和筏板基础的地基动态刚度计算公式为：

式中：Kφ，dyn为动态旋转刚度，N·m/rad;v为土壤泊松比;Es，dyn为土壤动态压缩模量，MPa;R为基础地面半径，m。

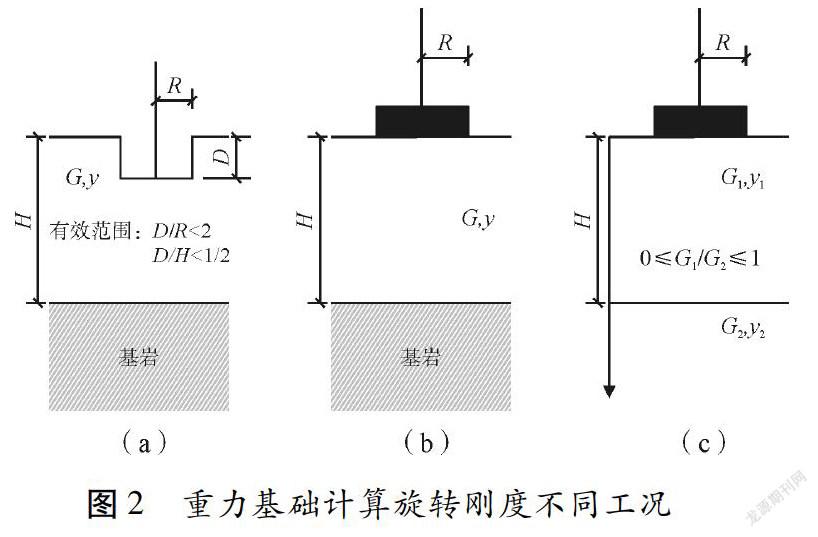
该公式无附图，土壤静态压缩模量没有定义，本文建议参考图2，R、Es，dyn取值参见IEC规范，挪威船级社规范DNV Riso 2002[10]规定，嵌入基岩上的地层中圆形地基旋转刚度：

参见图2，为方便比较，对公式格式进行了修改。该规范没有指出G的取值深度范围，一般取基础底面下有效影响范围内土体的平均G值，动、静态旋转刚度则按G0是否退化决定，见IEC。

式中：KR，dyn为倾覆力矩作用下动态旋转刚度;KR，stat为倾覆力矩作用下静态旋转刚度;G0为小应变剪切模量，MPa;G为剪切模量从G0减小到对应非零应变时的剪切模量，MPa;R为与地基接触的有效基础半径（如果在荷载下有间隙则取荷载方向接触宽度的一半），m。

该公式中动态旋转刚度采用S3荷载（正常工作状态），静态旋转刚度采用S1荷载（正常极端状态特征值）进行复核。动态旋转刚度采用G0，静态旋转刚度要考虑G0退化， 取Gr=0.1% 进行计算。如果有效R有减小，应采用缩减后的有效R计算。

针对风机基础的有限元方法通用表达式见公式（7）：

式中：H为基础所受水平外力，kN;M为基础所受弯矩，kN·m;δ为基础位移，m;θ为基础旋转角度;KL为水平位移刚度;KR为旋转位移刚度;KLR为耦合刚度。

刚度矩阵和岩土介质参数以及结构尺寸等有关，通常结构有限元软件采用质量-阻尼-弹性理论体系，岩土介质模型化为弹簧支承，岩土有限元软件则采用弹性半空间体系，岩土介质和混凝土结构均用单元链接，应力应变的关系取决于岩土介质的本构关系。有限元分析输出结果中包含了基础水平位移和旋转角度δθ，因此基础的水平位移刚度和旋转刚度可根据定义分别用式8、式9计算获得：

2 旋转刚度计算及分析

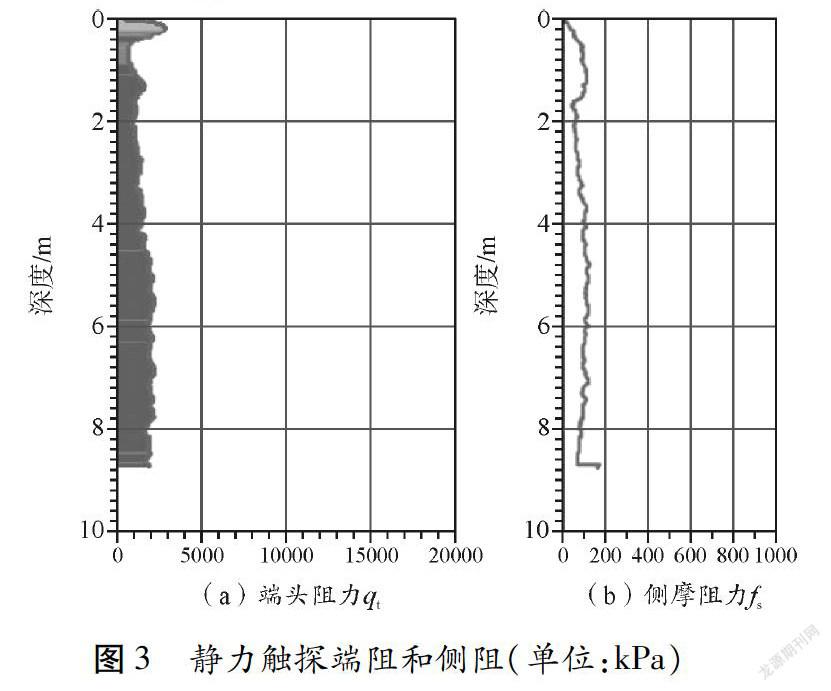
某风电项目拟安装共137组风机，其中某风机机组的荷载见表1。对每机组位置进行了静力触探测试，同时整个地勘包括了一定比例的标准贯入孔，多道瞬态面波物探试验，室内土工试验等等。场地以可塑到高塑黏土为主，塑性指数可高达50，对比地勘资料发现最弱地层发生在某孔，其静力触探地勘资料见图3，观测孔隙水位为地下-2.13 m。根据2.74 m和3.66 m处的土样，含水量约为25 %，液限为 68，塑性指数PI=52，土样干容重15.07 kN/m3，有侧限（82.74 kPa）的抗压强度qu=145.57 kPa。

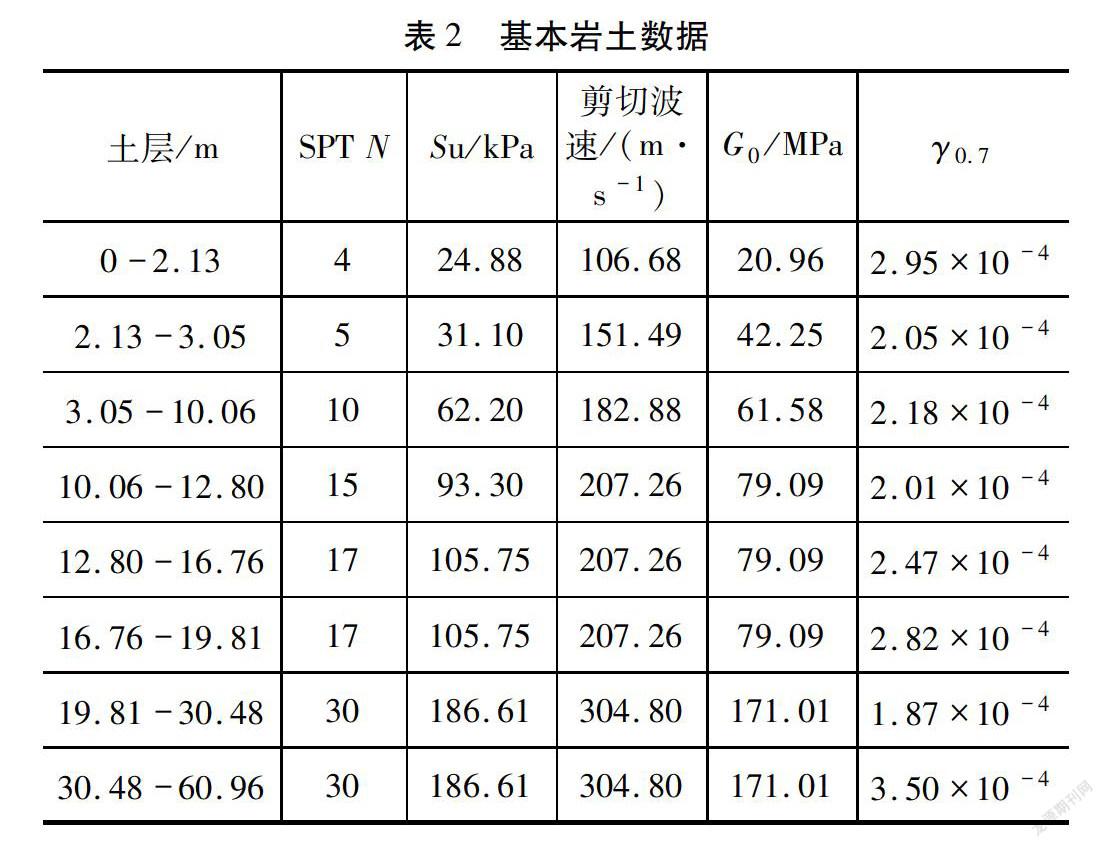
根据上述资料，岩土勘察提供的基本岩土数据见表2，基础确定采用重力基础，该机组重力基础嵌入深度2.8 m，高出地表0.15 m，基座直径5.49 m，基座高度1.07 m，基础底座直径（圆形底部）18.75 m，基础顶平直径（圆形）8.53 m，基础边缘厚度0.3 m，根据上述信息，基于三种规范的该基础的旋转刚度计算比较见表3。

为进行有关比较，利用Plaxis 3D对基础进行有限元分析，土的本构模型采用了小应变下软土硬化HSS模型，混凝土采用线弹性模型。土体采用立方体，从基础中心横向各延长三倍的基础直径因此边长达120 m，竖向采用60 m，见图4。

土体和基础均采用三维单元，精细尺寸，并全部互相链

（2）基础与地基没有脱开，有效半径均为基础底座半径;

（3）底层土剪切模量较大，故近似将最后两层土看作基岩。

接，该尺寸能有效降低土体的边界效应。基底设交互界面，并采用Rint=0.7。根据上述地勘报告内容，将土体从上到下按土的种类和软硬程度分成八层，具体岩土指标见前表。通过室内试验结果获得的参数包括不排水抗剪强度Su、ERef50、ERefOed和ERefur，这些参数可进一步用来校核没有室内试验

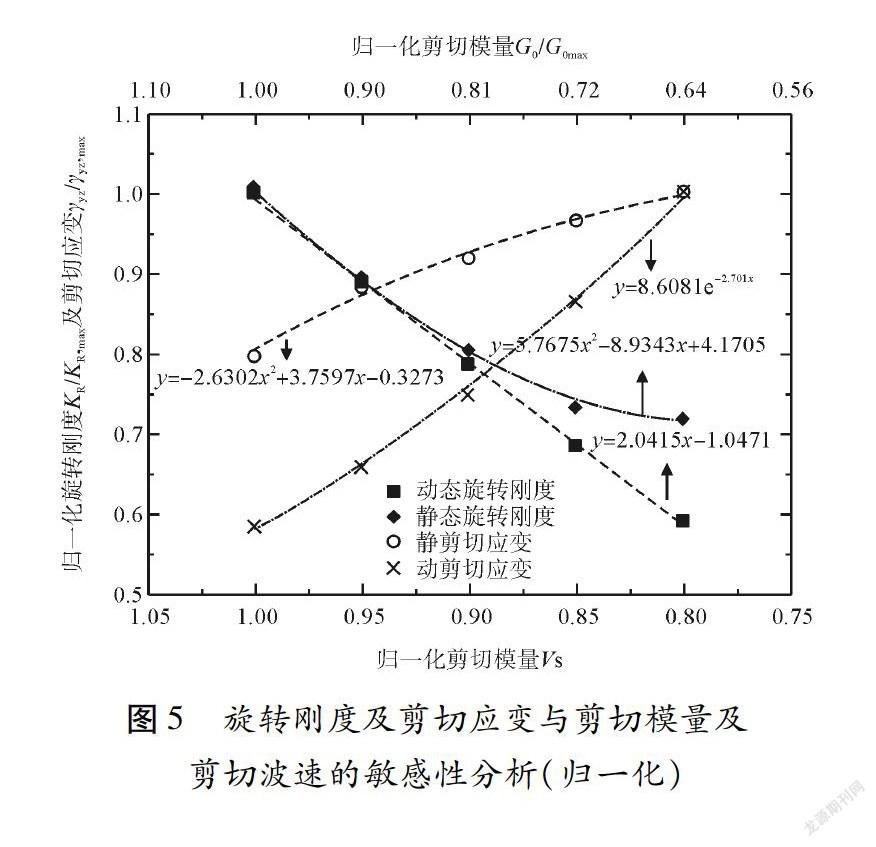
结果仅靠原位测试获得的参数。在校核中，注意试验土样的位置，通过调整E0/ERefur的比值，使得同一位置的基于原位测试数据相关参数和室内试验获得参数相同，通过ERefoed校核E0/ERefur的比值为5.95，将该值应用到所有土层，即可获得各土层的模型刚度参数，研究有限元计算结果对E0/ERefur比值的敏感性，计算结果见表4，有限元计算结果对Vs 和G0的敏感性见图5。

3 结 论

本文通过比较中国规范和国际规范对风电重力基础旋转刚度的异同，结果发现：

（1）国内规范，IEC 以及DNV规范中基础置于岩顶的计算结果和有限元计算结果非常接近，但国内规范没有考虑静态刚度计算。

（2）DNV规范中考虑基础嵌入情况下嵌入深度对基础旋转刚度的影响较大，后面的修正项几乎使得计算结果加倍。不考虑后面的修正项，和置于岩顶基础刚度接近。

（3）规范近似法动态旋转刚度计算均小于有限元動态旋转刚度计算结果，比值在0.85～0.90之间，但用近似计算法计算的静态刚度则比有限元计算结果较大，比值在1.3～1.4之间。

（4）通过对有限元土体硬化小应变模型参数的研究，发现重力基础的旋转刚度对HSS模型的刚度参数不敏感，对剪切波、剪切模量以及相关的弹性模量敏感，图5同时显示，归一化动态旋转刚度和归一化剪切波速/小应变下剪切模量呈现线性相关，归一动态剪应变则表现为二次多项式相关;静态旋转刚度和归一化剪切波速/小应变下剪切模量呈现多项式相关关系，当地基较硬时，近似线性相关，较软时则变化趋于平缓。

参考文献

[1] 王浩， 王炽欣. 风电场风力发电机组塔架基础设计研究[J]. 电网与清洁能源， 2008， 24（03）： 45-49.

[2] FD 003-2007风电机组地基基础设计规定[S].

[3] 庞作会， 李同舜. 陆上风机基础设计中应注意的几个问题[J]. 工业建筑， 2009， 39（S1）： 725-726+713.

[4] 章子华， 王振宇， 刘国华， 等. 沿海地区风机基础设计概述及工程应用[J]. 建筑结构， 2010， 40（S1）： 288-292.

[5] 许新勇， 刘峥， 张迪. 兆瓦级风机塔架基础地基力学特性研究[J]. 水力发电， 2012， 38（12）： 74-76.

[6] 水电水利规划设计总院. 陆上风电场风电机组地基基础设计规范（征求意见稿） [S]， 北京： 中国水利水电出版社，2016.

[7] IEC， 61400-6. Wind energy generation system -Part 6： Tower and foundation design requirements [S]， 2017.

[8] 王锡康. 对地基动刚度及惯性作用的研究[J]. 岩土工程学报， 1984， 6（4）： 76-85.

[9] JAlIbI S， SHADLOU M， BHATTACHARYA S. Wind Energy Engineering -A Handbook for Onshore and Offshore Wind Turbines[M]. T.M. Letcher Eds. London： Academic Press， 2017： 329-351.

[10] DNV &Riso. Guideline for design of wind turbines. 2nd Edition[S]. Denmark： JydskCentraltrykkeri， 2002.