仿机翼形便携式量水槽水力特性试验与数值模拟

贺梦杨，尚海鑫，张宽地,2※，凌 鹏

（1. 西北农林科技大学水利与建筑工程学院，杨凌 712100；2. 中国科学院水利部水土保持研究所黄土高原土壤侵蚀与旱地农业国家重点实验室，杨凌 712100）

0 引 言

灌区量水技术是实行计划用水的关键技术措施，对于现有量水设施来说，量水槽是灌区量水中较易使用、较易推广的一种明渠量水设施[1]。对量水槽的研究，文丘里于18世纪首先观测到水流通过局部收缩的管道时水流流速会增大，压强会降低，且研究了流量与压差的关系，提出了著名的文丘里流量计。Cone[2]首次提出文丘里量水槽，基于临界流的原理，通过测量水流流经不同几何形状收缩断面并产生临界流时的水深来计算流量。Parshall[3]改进文丘里槽，将其命名为巴歇尔量水槽，给出了含有水深的流量计算公式。Skogerboe等[4]进一步研究了巴歇尔量水槽在不同工况下的水力特性。巴歇尔量水槽在淹没度大于0.95的工况下，测流精度会有明显的降低[5-7]，而且在实际工程应用中会有造价高等不利因素[8-9]出现。

从经济实用等角度考虑，传统的侧壁收缩式量水槽在小截面渠道中应用受限，Hager[10]在常用的3种渠道形式中，首次提出了便携式装置的概念，渠道中心放置易于调节位置的圆柱体替代侧壁收缩的形式，以收缩渠道宽度。Hager[11]重新考虑了圆柱体放置在渠道中的情况，并提出了采用上游能量值的测流方法。Samani等[12-13]研究表明，利用收缩断面来获得临界流水深是最简单的测流方法，这一方法可以形成短喉道的量水槽而且不再需要过长的入流和出流段，得到了误差为5%的测流公式。Badar[14]利用Samani等[13]的数据，改进试验方法后将测流误差降低到了4.7%。

随着计算流体力学在量水槽研究中的广泛应用，Wright等[15]首次利用数值模拟的方法分析了巴歇尔量水槽中不同流体性质对水深流量关系式的影响。肖苡辀[16]基于FLOW-3D进行了田间便携式短喉槽的研究，总结其在末级渠道测流适用性。Kolavani等[17-18]研究了中央折流板水槽不同几何参数的影响，并提出了一种显式的阶段-流量关系。Hager[19]研究了临界流条件下圆锥浸入矩形渠道的过流情况，Kapoor等[20]在此基础上，在矩形水槽中提出了圆锥形便携式水槽测流装置，可作为小型矩形明渠临时测流装置。Samani[21]提出3种标准渠道下的便携式量水槽，无论水槽或过流尺寸如何，都可以使用已校准的方程式进行测流，并且通过试验进行了验证。Ghare等[22-23]提出具有可移动，易安装等优点的圆柱形量水槽，提出了最大测流误差为5%的测流公式，可以作为临时测流的移动装置。

现有的由文丘里流量计原理设计所得的明渠测流装置，安装维护都需要相当高的费用，且为固定装置，通常需要预制水槽。传统的固定式量水槽是为了准确测量大断面渠道（干渠或主要支渠）流量，目前对于这类渠道的流量测量比较精准[24]，但是对于小截面的渠道（散户田间地头用水）来说并不具有成本效益。吕宏兴等[25]根据美国国家航空咨询委员会（National Aviation Advisory Committee，NACA）发布的机翼形厚度的参数表达式，结合小阻力曲线量水技术，提出了机翼形量水槽。为解决机翼形量水槽施工和制图过程较复杂的问题，同时探索新的量水装置设计思路，本文在机翼形量水槽的研究基础上，简化了机翼形复杂的曲线方程，得到双弧形结合的曲线型量水设备，并设计仿机翼形便携式量水装置，通过在矩形水槽中进行水工模型试验，结合FLOW-3D数值模拟结果建立测流公式并对其进行验证。该研究可为改进量水方法、提高用水效率提供设计参考，对促进中国灌区小截面便携式量水槽的推广具有实用价值。

1 仿机翼形便携式量水槽

1.1 简化过程

机翼形量水槽是由吕宏兴等[25]根据文丘里量水槽研究出的一种量水槽。其机翼形曲线多项式方程为

式中P为翼高，m；C为翼长，m；x为横坐标值；y为纵坐标值。

翼高和翼长是机翼形曲线变化的主要控制参数，在对机翼形的简化过程中，保持原有翼长C和翼高P不变，喉口位置保持在0.3C处。为满足原有机翼形光滑连接要求，并且使y值误差较小，选用椭圆弧和圆弧的连接方式，即喉口断面上游用1/4椭圆弧代替，下游用一段相切的圆弧代替。图1a为现有机翼形和简化后的对比，实线为机翼形，虚线为简化后所得仿机翼形，图 1b为收缩比0.5、翼高15 cm、翼长70 cm的模型简化图。

仿机翼形量水槽上游1/4椭圆方程和下游圆弧半径R（m）分别为

1.2 简化后量水槽结构

仿机翼形量水槽合并后中轴线与矩形水槽中轴线重合（图2），称为仿机翼形便携式量水槽。合并体形宽度最大宽度B为

2 水工模型试验

2.1 模型试验布设概况及试验过程

试验于西北农林科技大学水工水力学实验室进行，试验渠道长17 m，宽70 cm，高100 cm，平坡，断面形状为矩形（图3）。根据试验渠道和长度和宽度，为保证足够的过水宽度和平稳的水位测点，选择翼长为70 cm、6组不同收缩比的试验模型（表1），模型材料为木制空心，外部包裹有不透水铁皮。根据中国农田常用灌溉流量范围10～50 L/s，每组模型设置7组不同的流量，分别为15.3、19.4、25.0、30.6、35.1、41.7和47.2 L/s，共设计试验方案42种。采用SCM60型水位测针测量其对应的上游测点水深（距上游进水口5 m）、喉口水深（距上游进水口10 m）和下游水深（距上游进水口15 m）。5和15 m测点处测量左中右三点水深并取平均值，其中5 m测点处结合相同测点水深计算佛汝德数；10 m测点处分为两个流道，分别测量各流道左中右水深并取平均值，根据流速和上游测点处水深，计算上游佛汝德数。

式中v为量水槽上游流速，m/s；g为重力加速度，m/s2；H为上游测点水深，m。试验所取收缩比及对应量水设备宽度见表1。

表1 试验模型参数表Table 1 Parameter table of test models

2.2 水工模型试验结果分析

2.2.1 上游佛汝德数

在明渠测流中，佛汝德数是一个重要的无量纲数，保证测流精度的重要条件。上游佛汝德数过大，会导致水面波动较大，给水深的测量带来较大的误差。

由试验数据可以看出，所有工况下佛汝德数均小于0.5，满足测流规范要求[26]。总体上，佛汝德数随着收缩比的增大而增大，并且随着流量的增大呈先增大后减小的变化趋势（图4）。当流量达到25～30 L/s时，佛汝德数达到极大值。因此量水槽适宜收缩应该小于0.709，以保证满足测流精度和渠道安全的要求。依据本次试验数据结果，收缩比在不小于0.537的条件下，上游佛汝德数均可以满足测流规范。

2.2.2 壅水高度

水流从上游流入量水槽，由于量水槽束窄渠道，流速迅速增大，水位随之降低。水流经过量水槽后渠道变宽，流速下降，水位升高，水流汇集形成水跃。在这个过程中，上游的水位由于一定的阻水作用会有所升高，即壅水高度Hy（m），指在水流流态稳定后上游水深H（m）与下游水深h（m）的差值

结果表明，仿机翼形量水槽的上游壅水高度最大值为6.32 cm，最小值0.46 cm，平均值3.25 cm，该量水槽的上游壅水高度比较小（图5）。总体上，壅水高度随着流量的增大而增大，随收缩比增大而减小。根据连续性方程，渠道内流速增大，量水槽上游的阻水作用会引起动能转化为势能，导致水流势能增加，水深增加，上游壅水高度增大；收缩比越小，过流断面面积越小，对量水槽上游的抬升作用就越强，上游壅水高度越大。本次水工模型试验所有工况条件下，壅水高度均小于7 cm。双流道输水壅水高度略大于单流道壅水高度，为满足渠道上游安全需求，尽量减小壅水高度，适宜收缩比范围为0.606～0.709，收缩比0.606条件下的平均测流误差为6.95%，收缩比0.709条件下的平均测流误差为4.91%。此收缩比范围条件下，试验所得数据壅水高度小于5 cm。

3 仿机翼形便携式量水槽水力特性数值模拟研究

本研究采用数值模拟方法，基于FLOW-3D进行仿机翼形量水槽研究，首先将数值模拟和模型试验所得数据中的上游和喉口水深进行对比，验证模拟的准确性后，进一步分析水工模型试验中较难得到的水力学参数，减少试验的时间和成本。水工模型试验共设计6组收缩比、1组翼长、7组流量工况条件下的仿机翼形量水槽。在重复水工试验模型的42种工况后，数值模拟增加2组收缩比（0.550、0.630）、3组翼长（65、75、80 cm）的数值模拟模型，并选取与水工模型试验相同的7组流量。

3.1 模型建立

根据设计的量水槽具体尺寸，利用AutoCAD分别建立不同收缩比的量水槽三维数值物理模型。模型进水口的右下角放置于坐标原点。X轴正方向为水流的流向，Y轴正方向指向渠道左壁，重力加速度反方向为Z轴正方向。由于水工模型试验中水深均不超过30 cm，为提高数值模拟的准确性和效率，将矩形水槽高度由100降低至30 cm，以减少固定网格数。其余各选项设置均为默认。

3.2 网格划分以及边界条件的设定

FLOW-3D中采用FAVOR技术对模型进行网格划分。采用六面体网格，覆盖全部模型的网格单元边长为2 cm；总网格数量为315 760个。设置上游进口流量进口边界，不设定液面高度和内容填充，默认水流沿与边界垂直方向流入且整个边界充满流体；下游出口设置为自由出流边界；渠道底部以及侧壁均选择墙边界；渠道顶部设定为对称边界，即无液体穿过该边界。除此之外不做任何设置。

3.3 计算模型选取及数值求解

选取重力模型和湍流模型进行数值模拟求解计算。其中，重力模型中只对重力进行设置，在Z方向上设置其为-9.81 m/s2；采用RNGk-ε湍流模型进行数值模拟，各项参数默认。默认使用有限差分法将模拟控制方程处理为代数方程组后求解计算，对流项默认即采用二阶迎风格式离散，扩散项默认即采用二阶中心差分格式离散，迭代的最小步长值设为10-6s，数据写入时间间隔为2 s。采用TruVOF方法[27]加速对模型自由表面的处理，大大减少计算模型时达到稳定状态所需的时间，也保证了计算精度。

3.4 数值模拟结果验证

在水工模型试验中测量渠道上游和喉口处测点水位，将其与数值模拟结果对比，以得到本次数值模拟的准确性。上游测点处水深实测值与模拟值的误差均能控制在4.50%以内，最大值为4.48%，最小值为0.29%，均值为1.56%；喉口测点处水深实测值与模拟值的误差均能控制在5.50%以内，最大值为5.10%，最小值为0，均值为2.26%。对比结果证明了FLOW-3D在计算上的准确性，具体如表2所示。

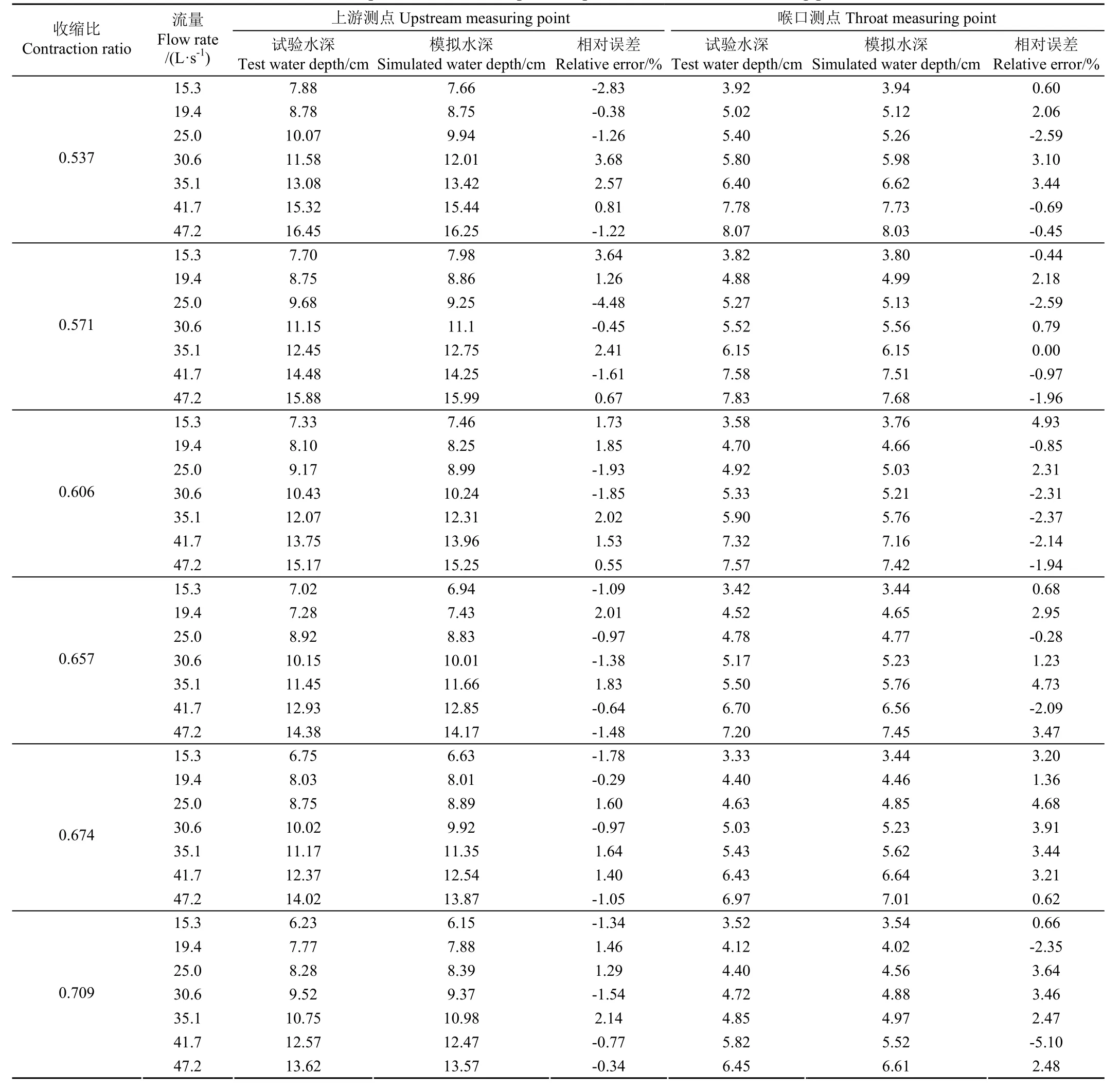
表2 上游、喉口测点处水深对比Table 2 Comparison of water depths at upstream and throat measuring points

3.5 数值模拟结果分析

3.5.1 佛汝德数

根据数值模拟的结果，对矩形渠道整体区域的佛汝德数进行分析。明渠量水槽的槽前佛汝德数应小于0.5，以保证上游水流流速不会过大导致形成驻波。在模型试验中，验证了所有试验工况下上游水深测点处的佛汝德数，均满足测流规范。在水流稳定的情况下，流量为30.6 L/s、收缩比为0.571工况下的沿程佛汝德数见图 6。从水流的流态方面考虑，水流在进入量水槽前均属于缓流，在量水槽入口处渠道变窄，水流流速增大且水深减小，佛汝德数开始增大；在喉口段附近，水流为临界流，佛汝德数等于1；水流经过束窄段后仍在加速，水深继续降低，水流流态为急流；发生水跃后，由于水流质点相互冲击消能，流速减缓，水深增加，水流重新变为缓流，佛汝德数小于1。

3.5.2 流速分布

仿机翼形量水槽的上游水流稳定，流速变化较小。主要研究收缩断面及其下游的沿程流速变，分析流量30.6 L/s，收缩比0.571的工况，得出沿程流速分布情况（图7）。水流从量水槽上游接近量水槽入口时，由于渠道过流面积减小，水流流速增大；喉口段，水流继续加速，但是由于两侧水流受边壁束窄影响较大，在同样长的时间内，两侧水流流过更长的距离，因此两侧水流流速大于中部水流；到达水跃附近断面，水流加速，在仿机翼形尾部，发生水跃处（部分工况）流速达到最大值，但是由于已经处于量水槽下游扩散段，两侧的水流因为汇聚的相互碰撞，流速开始减缓；量水槽下游，过槽水流继续扩散，两侧水流与中部水流流速均减缓，水流有继续向外扩散的趋势，受到渠道边壁阻挡，水流重新向中部交汇，水流总体逐渐恢复稳定。

3.5.3 流线分布

流线分布可以直观地反映出流场中水流的流动趋势，结合流速分布可以得到水流流态的变化情况。设置与流速分布计算时相同的工况，绘制出水流的流线（图 8）。量水槽上游，流线顺直，相互平行，且流速较低；量水槽入口段，由于渠道的束窄作用，流线沿量水槽边壁开始向内弯曲，越靠近渠道侧壁弯曲越明显；水流进入两侧束窄段后，流速增大，在量水槽末端流速达到最大值1.13 m/s；进入下游扩散段，两侧水流流线沿量水槽边壁向渠道中轴线汇聚，流速减小，水槽中部水流在左右水流汇集和水跃的影响下，流线交错混乱，流速为最小值0.05 m/s；在量水槽出口处，两侧水流继续向中间汇聚，流线向中部弯曲，中部水流流线与两侧水流流线相互交汇，中部水流流速增大，流线回归平稳。

3.6 测流公式的建立及误差分析

本研究矩形渠道中有2个对称的流道，与机翼形量水槽单流道过水方式不同。机翼形量水槽的测流公式推导过程中，涉及到的参数均与过水流道数量无关，变量为过水横截面宽度，可以采用双流道过水横截面的最小宽度之和代替原公式中单流道过水宽度。采用吕宏兴等[25]在机翼形量水槽量纲和谐的测流公式（7），计算本研究所得水深与流量关系：

式中Q为流量，m3/s；Bc为最小过流宽度，m；H为上游水深，m；a、n为常数，通过水工模型试验和数值模拟所得数据分析确定。在对数坐标系中有[18]式中Hk为过水截面最小宽度处水深即临界水深，m，在对数坐标系中，采用水工模型试验和数值模拟所得到的共84种工况下获得的上游水深和临界水深拟合分析获取公式，绘制出其对数线性关系，在常规坐标系中进行线性拟合，即可获得n和a的值。

不同翼长、不同收缩比和不同流量工况下所有数据均呈现非常好的线性关系（图9），拟合得到n=0.928 2，a=0.516 4。

将上述结果代入式（8）中，得到矩形渠道仿机翼形便携式量水槽测流公式为

将水工模型试验测得42组上游水深代入式（9）中，所得计算流量与实测流量平均相对误差为6.34%（表3），满足中国农田灌区测流精度的要求。

表3 实测流量与计算流量误差Table 3 Measured flow and calculated flow error

4 讨 论

机翼形量水槽相比于其他量水设备具有水头损失小、渠道阻水小、流量计算公式简单、壅水高度小等优点。本研究对固定式机翼形量水槽简化设计后，得到仿机翼形便携式量水槽。便携式量水设备主要适用于末级灌区德小型渠道。通过分析水工模型试验和数值模拟的结果，发现简化并没有改变原机翼形的固有优点，而且施工简单，测流精度高。Di Stefano等[28]在Samani等[12-13]工作的基础上得到矩形渠道圆柱形量水槽测流公式，其中流量Q是H与Bc的函数，与本研究所得测流公式形式一致，测流误差也略高于仿机翼形量水槽。该研究测流公式是由喉口水深和上游水深拟合得到的，水工模型试验中双流道水深测量共6次，由于模型制作不规则和与渠道中轴线未完美重合等原因，导致双流道喉口水深测量出现了误差，导致部分工况下的测流误差较大。本文分析了仿机翼形量水槽壅水高度等特点，分析了其泥沙不易淤积的水力特性，但是并未进行含沙水流试验，研究方法还有待改进。该研究采用Flow-3D软件，RNGk-ε三维湍流模型进行数值模拟，相较于标准的k-ε模型可以更好地处理高应变率以及流向弯曲程度较大的流动。TruVOF方法较传统的VOF方法提高了收敛效率，对自由液面的描述也更加精确。网格划分所采用的FAVOR技术，可以用较少的网格处理不平整的区域，在保证运算精度的前提下尽量少地占用资源。从沿程佛汝德数、水流流线等水力性能细节分析，数值模拟方法相较于传统的水工模型试验更有优势，为解决灌区量水问题提供了更高的精度和效率，也可为量水槽体型优化和简化提供便利。

5 结 论

依据现有量水槽研究的实际情况，本研究采用水工模型试验与数值模拟相结合的方法完整的研究了仿机翼形量水槽的水力特性，主要研究结果如下：

1）仿机翼形量水槽有较大的自由出流范围，测流灵活性强。仿机翼形量水槽的槽前壅水高度最大值6.32 cm，最小值0.46 cm，均值3.25 cm。壅水高度较小，有利于减小渠道施工挖方量和渠道材料用量。量水槽计算所得佛汝德数均小于0.5，满足测流规范要求。

2）利用FLOW-3D软件增加了3组量水槽翼长、2组收缩比的矩形渠道仿机翼形便携式量水槽数值模拟。结合机翼形量水槽的测流公式，拟合获得其各参数值，得到仿机翼形量水槽水位流量公式。所得仿机翼形量水槽测流公式精度高，平均测流误差为6.34%。

3）本次研究仿机翼形便携式量水槽工况流量范围为15.3～47.2 L/s。壅水高度和佛汝德数等水力参数限制下，建议选择收缩比范围0.606～0.709，收缩比0.606条件下测流平均误差为6.95%，收缩比0.709条件下平均测流误差4.91%。本次研究翼长范围为65～80 cm，均满足灌区量水要求，实际工程中渠道宽度为70 cm时，建议翼长范围65～80 cm。