基于EEMD-多尺度排列熵-SVM的小电流系统故障选线仿真*
2021-09-15林海涛曹春诚
林海涛 曹春诚
(国网呼伦贝尔供电公司 呼伦贝尔 021100)
1 引言
我国的配电网主要应用小电流系统,又称为中性点不直接接地系统。在小电流接地系统中,单相接地故障发生的概率较高,2h~3h不能排除故障的话,将会带来更加严重的后果,影响电网正常运行。小电流系统发生故障时,故障信号微弱,线路上的电流变化不明显,零序电流也呈现出复杂的非线性f和非平稳性,给故障选线带来困难[1~4]。
目前国内外故障选线主要分为两大类,一是利用稳态信号的大小和相位方向进行故障选线;二是利用暂态信号的突变量、大小、相位、能量进行选线。相对于稳态故障选线法,暂态信号的信息量更加丰富,故障特征也更加明显,因此暂态选线法得到更多的认可,目前的选线方法有信号注入法,通过电压互感器向线路注入特定频率的信号完成选线,但是注入法受到高阻接地限制;零序电流幅值法,利用故障时零序电流幅值最大完成选线,但是在谐振接地系统中,该方法失效;小波变换法,根据小波变换的分频特性,将信号投影到小波频带上,根据频带上信号的大小和极限的比较,判断故障线路[5~7],在中性点不接地和消弧线圈接地系统中得到应用,但是短路时暂态信号有随机性,如果暂态信号太小,小波分析法会有很大的误差。受过渡电阻干扰,信号对突变信号干扰影响也比较大;Prony算法此算法分析小电流系统的故障电流有很好的普适性,当小电流系统发生单相接地故障时,故障电流的幅值、频率、阻尼系数等参数和故障的特征有很好的相关性,该算法可以分析直流分量的阻尼和高频率分量的频率,通过这样的特征就可以实现故障选线了,但是Prony算法需要很大的计算量,而且对微机的性能具有较高的要求;行波法故障测距用的是故障的时候所产生的行波信号,当线路发生故障时,会在线路两端传递暂态行波信号,其中包括单端法和双端法,行波法在分支少和较长线路的输电线路具有很好的适应性,但是如果配电线路结构复杂,分支多的短线路,则识别会困难,而且需要很多行波检测设备,经济成本也会很高,因此在配电网中行波法很难适用[8~11]。
提出EEMD-多尺度排列熵-SVM选线方法。EEMD算法是通过对原始多次加入白噪声之后在进行EMD分解,将所得结果平均得到各个固有模态函数,EEMD算法抑制了EMD算法的模态混淆问题,通过EEMD算法对信号分解,可以得到从高频到低频的固有模态函数,并且所得结果相比于EMD算法更具有固有模态函数性质。多尺度排列熵是一种动力学突变检测方法,可以对信号复杂程度分析较为理想,可以充分分析信号的特征。SVM对解决非线性、高维度样本分类,分类效果良好。
用EEMD对各线路的零序电流进行精细的分解,得到各固有模态函数,用多尺度排列熵计算各线路的固有模态函数各个尺度下的排列熵,将计算出来的多尺度排列熵作为SVM的输入,通过SVM输出的分类标签判断故障线路。
2 EEMD分解方法
由于EMD算法处理暂态信号时会受到突变干扰,出现模态混淆问题,使所得的固有模态函数分量失去信号本身的物理意义。而EEMD算法通过添加不同的高斯白噪声和多次集合平均克服了EMD的模态混淆问题。具体步骤如下。
1)在信号x(t)叠加高斯白噪声ni(t),其中高斯白噪声的均值为零,标准差为信号x(t)的0.2倍,即:
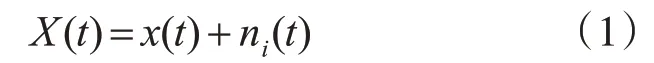
2)用EMD算法分解X(t),得到各固有模态函数分量,即:

其中,ch(t)为EMD第一次分解得到的h个固有模态函数分量,rn为余项。
3)在x(t)中再次加入高斯白噪声,重复上述步骤1)、步骤2)。
4)重复步骤k次,会得到k组IMF分量,将所得结果平均。得到的固有模态是按照高频到低频顺序排列的。
3 多尺度排列熵
多尺度排列熵是对排列熵的一种改进,首先需要对时间序x(i)列粗粒化,即:
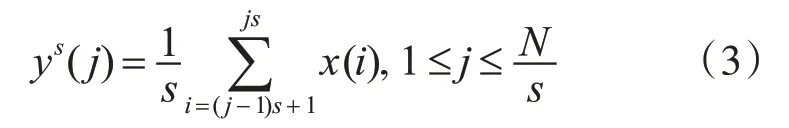
式中,s代表尺度因子,ys(j)代表多尺度下的时间序列,对时间序列进行重构得到:
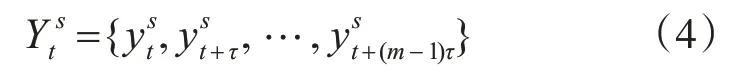
其中,m代表嵌入维数,τ代表延迟时间。将(4)按照升序排列,则多尺度时间序列有m!种排列方式,计算各个尺度下时间序列的概率:
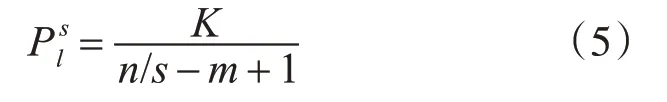
其中,K代表每种类型出现的次数,则各尺度下的排列熵为
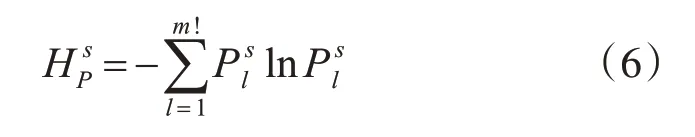
将式(6)归一化,即:

多尺度排列熵可以衡量时间序列的复杂程度,不同故障情况下,各个零序电流的时间序列测度设不同的。小电流系统故障时,会产生各线路不对称运行,会产生零序电流,用EEMD算法对零序电流分解,得到各个固有模态分量,取各个线路分解后的固有模态函数,计算多尺度排列熵。其中粗粒化过程十分关键,即尺度因子的选择尤为重要,通过多次实验发现,尺度因子取5时,实验效果最佳。计算出来的多尺度排列熵作为SVM的输入。文中采用遗传算法改进的SVM。
4 GA-SVM算法
SVM可以解决非线性、高维度样本的分类,对于小电流系统故障各线路的信号多尺度排列熵有良好的分类效果。SVM需要构造一个分类超平面:
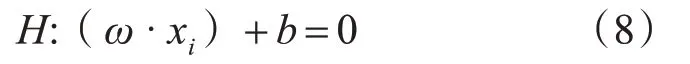
通过相应的约束条件得到分类间隔:

在对样本完成分类时,需要加入从松弛变量和惩罚因子,得到最优的超平面:
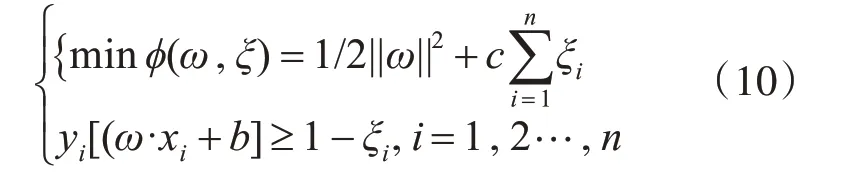
其中,ξ为松弛变量,c为惩罚因子,x,y为输入样本。
RBF为SVM的核函数,其中的盛饭系数和核参数都需要进行优化,本文采用遗传算法对其进行优化。遗传算法具有自适应全局搜索能力,是模拟生物界遗传和进化而得到的算法,通过遗传算法对SVM进行优化可以使得SVM分类更加准确,提高故障选线能力。具体步骤如下:
1)通过对惩罚系数和核参数编码,生成初始种群。
2)用多尺度排列熵作为样本对SVM进行训练,得到分类结果,计算分类的准确程度,建立适应度函数。
3)满足停止条件时,得到优化后的惩罚系数和核参数,如果所得结果不满足,进行下一次遗传迭代。
5 仿真验证
配电系统选择四条线路,线路长度分别为10km、25km、35km、40km,系统采用经消弧线圈接地方式,其中采用10%的过补偿,因此取消弧线圈的电感L=0.9459H,线路的正序和零序参数如下所示。
R1=0.01273Ω/km,R0=0.3863Ω/km
L1=0.9337mH/km,L0=4.1264mH/km
C1=12.74nF/km,C0=7.751nF/km
假设线路1的A相在出线的20km处发生接地故障,且接地电阻为50Ω,各线路零序电流如图2所示。

图1 配电系统仿真模型
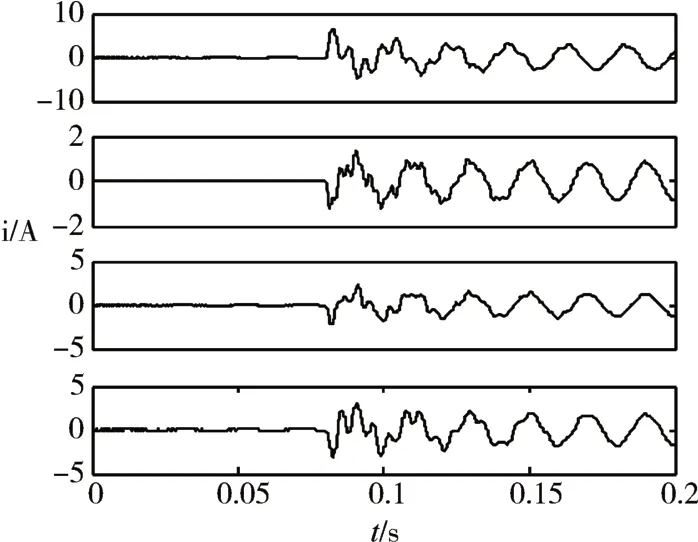
图2 障后各线路零序电流
图2是故障后各线路零序电流,线路1为故障线路,可以看出线路1零序电流的极性与其余线路相反,且线路1零序电流幅值为其余线路零序电流之和。用EEMD算法对各线路零序信号分解如图3所示。
图3是各个线路零序电流EEMD分解的结果,可以看出分解的结果逐渐的变平滑,选取IMF4、IMF5叠加各线路的特征量,计算各线路固有模态函数的多尺度排列熵,所得结果如图4所示。
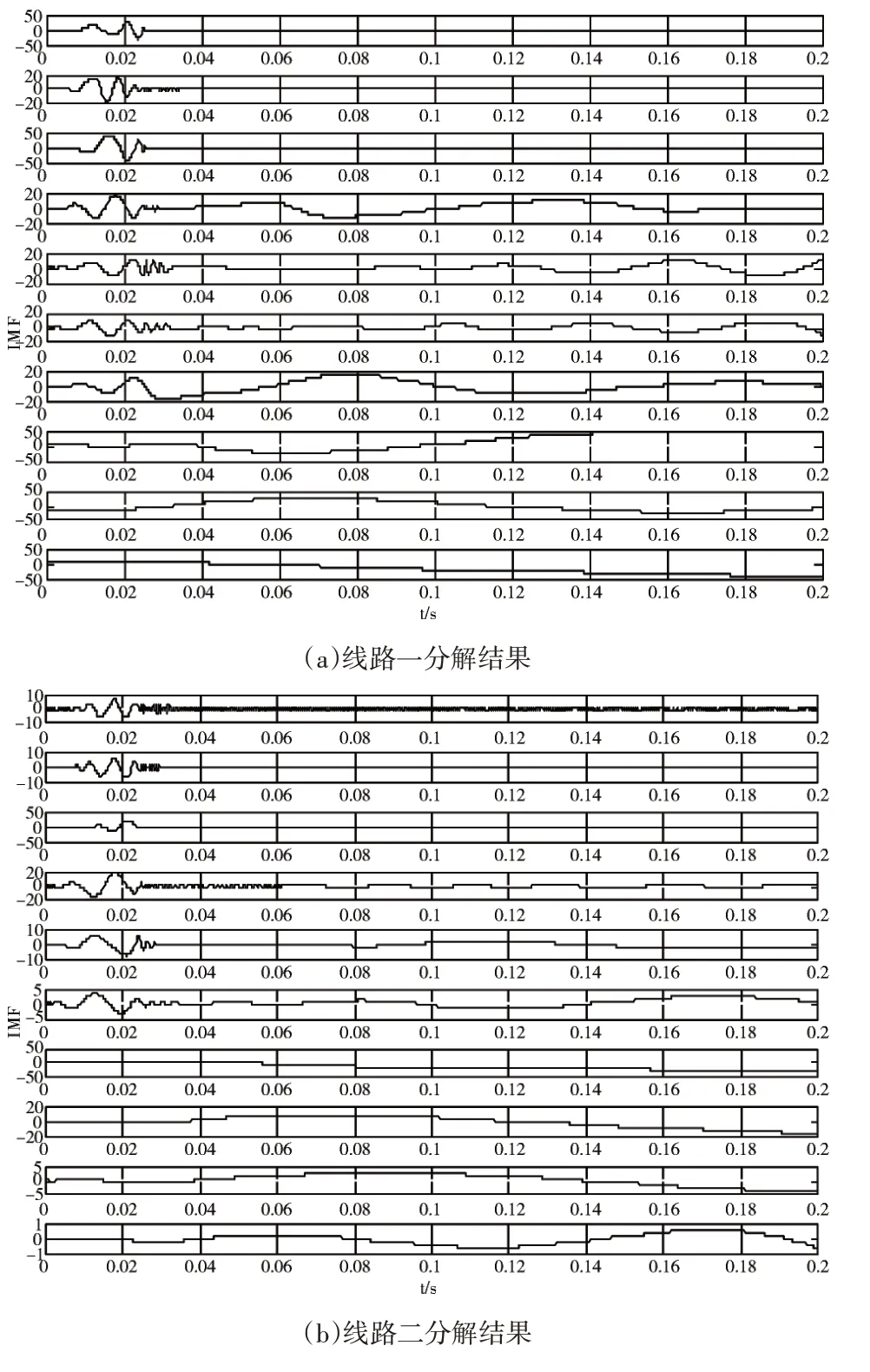
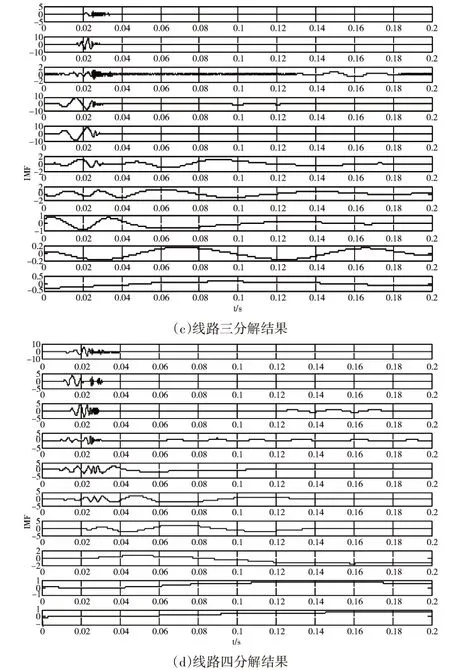
图3 EEMD分解结果
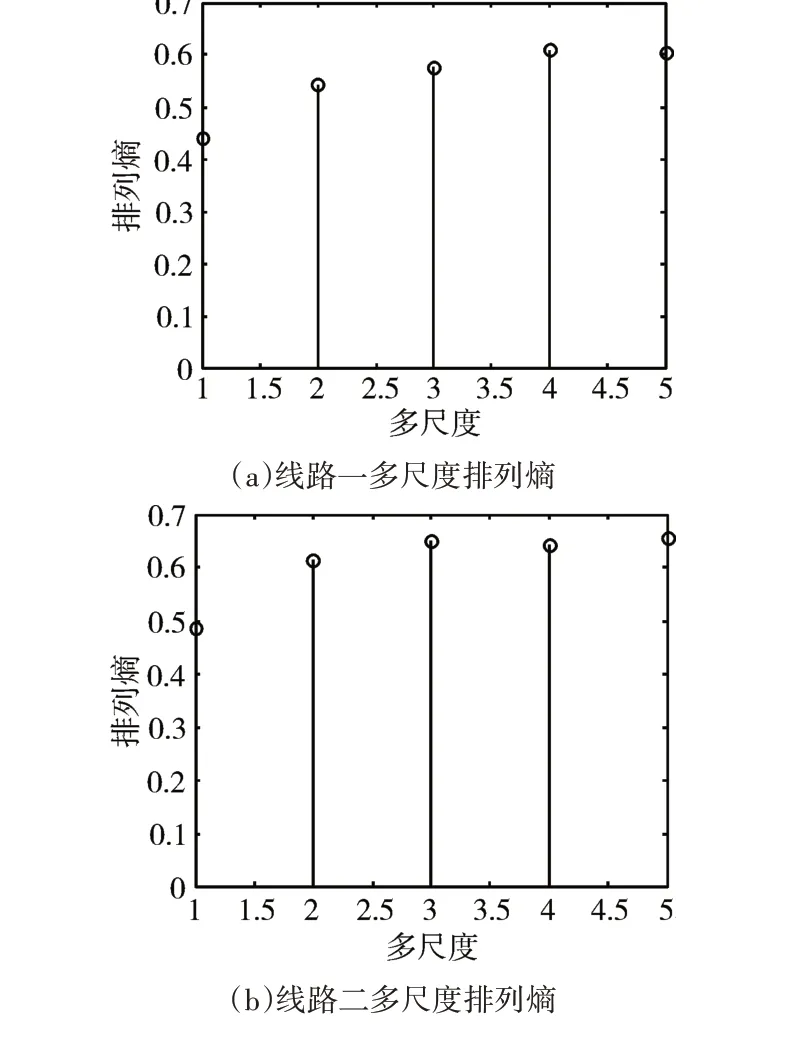
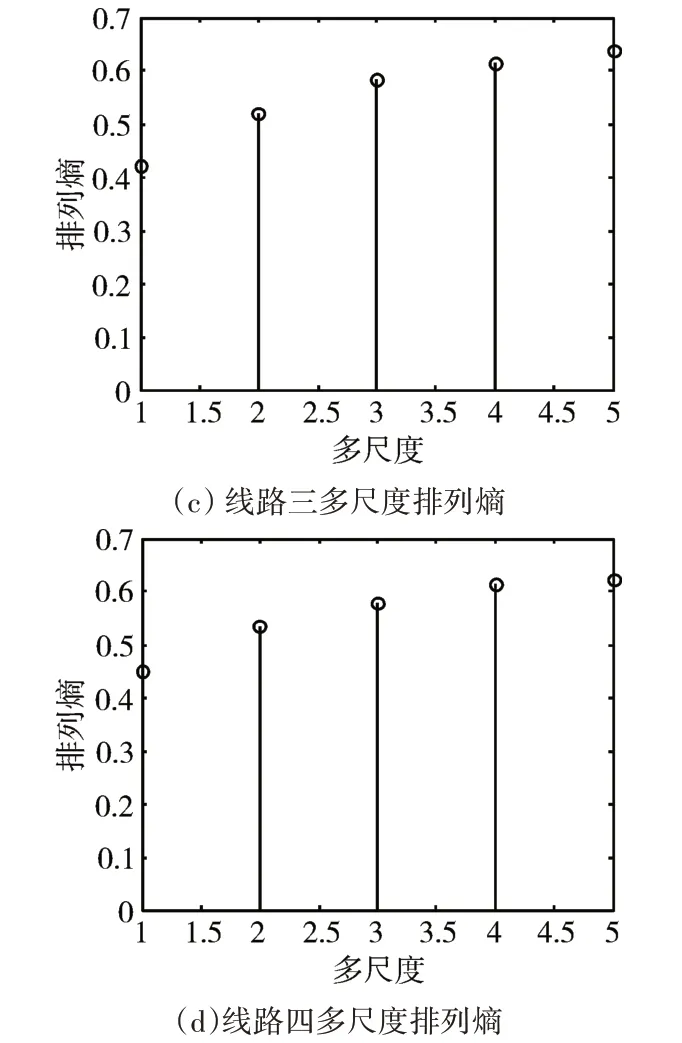
图4 各线路多尺度排列熵
采用遗传算法优化SVM对所提取得多尺度排列熵进行分类,对样本进行分类标签,其中故障线路设为1,正常线路设为2。
将图4的多尺度排列熵输入到已经训练好的GA-SVM中。其中遗传算法的种群规模取为100,迭代300次,交叉概率为0.6,变异概率为0.3。算法从线路1到线路4的输出结果分别为1,2,2,2。则线路一为故障线路,与初始设置的故障线路一致。
因为实际中高阻接地情况较为普遍,补充1000Ω接地实验。
图5是高阻接地故障后各线路零序电流,线路1为故障线路,可以看出线路1零序电流的极性与其余线路相反,且线路1零序电流幅值为其余线路零序电流之和。用EEMD算法对各线路零序信号分解如图6所示。
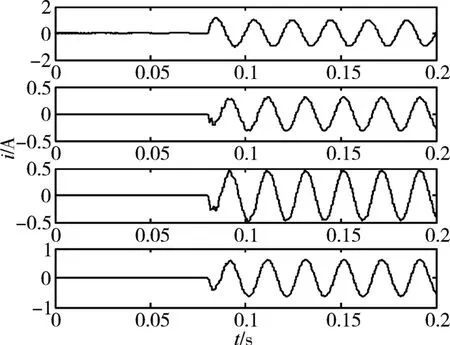
图5 故障后各线路零序电流
图6是各个线路零序电流EEMD分解的结果,可以看出分解的结果逐渐的变平滑,选取IMF4、IMF5叠加作为各线路的特征量,计算各线路第一固有模态函数的多尺度排列熵,所得结果如图7所示。
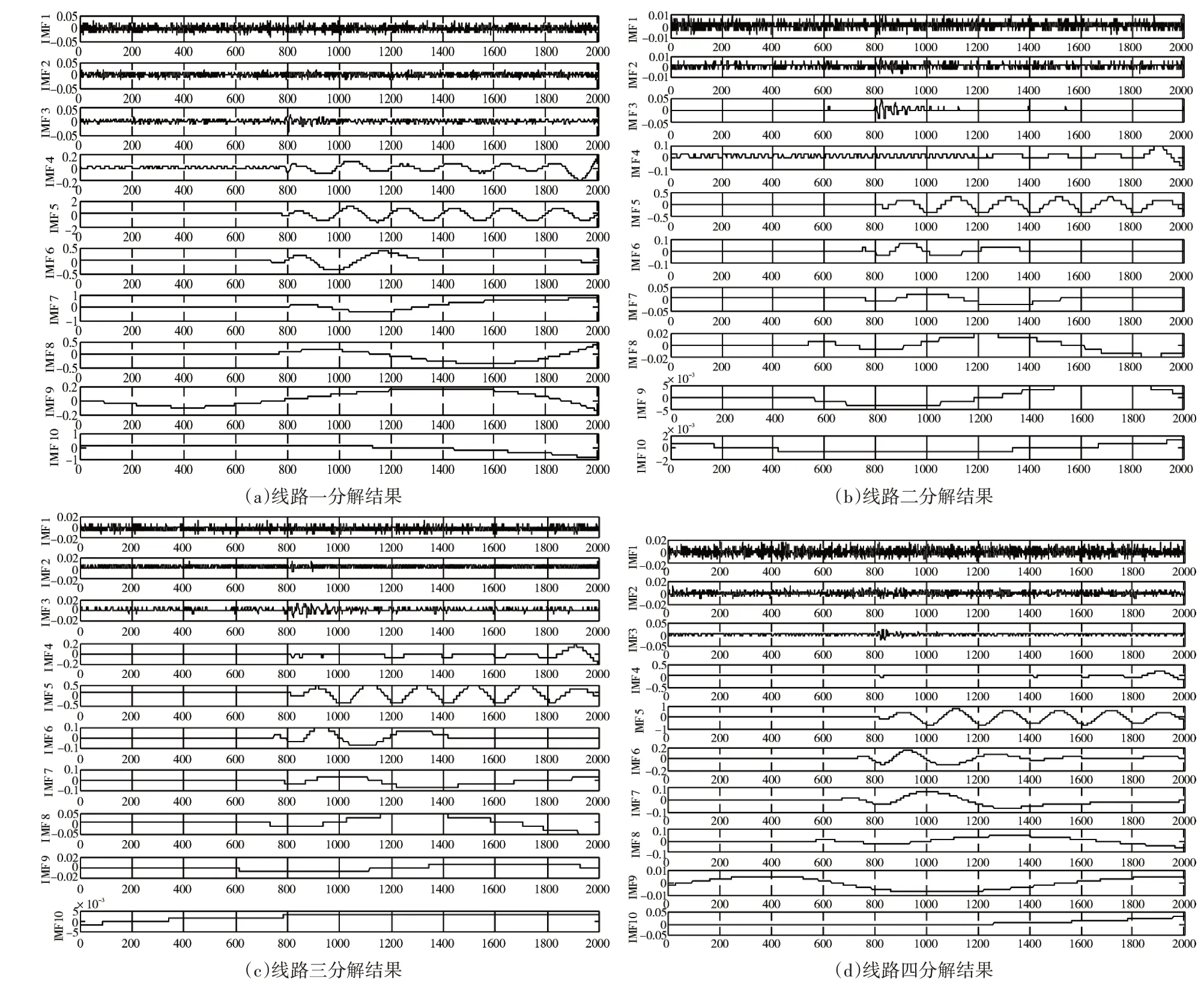
图6 EMD分解结果
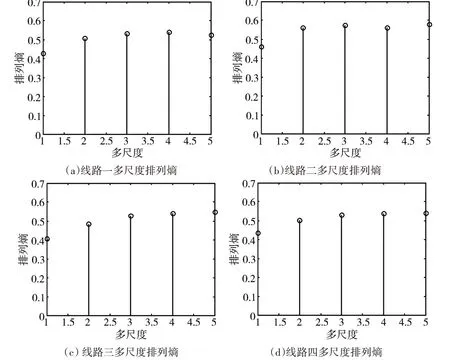
图7 线路多尺度排列熵
采用遗传算法优化SVM对所提取得多尺度排列熵进行分类,输出结果分别为1、2、2、2。则线路一为故障线路,与初始设置的故障线路一致。
故障线路、合闸时间、短路距离的不同对选线结果都会产生影响,为此都进行了仿真实验,结果如表1所示,从表中可以看出,本文所提出的选线方法并没有出现错选或者漏选,对故障选线有较高的可靠性。
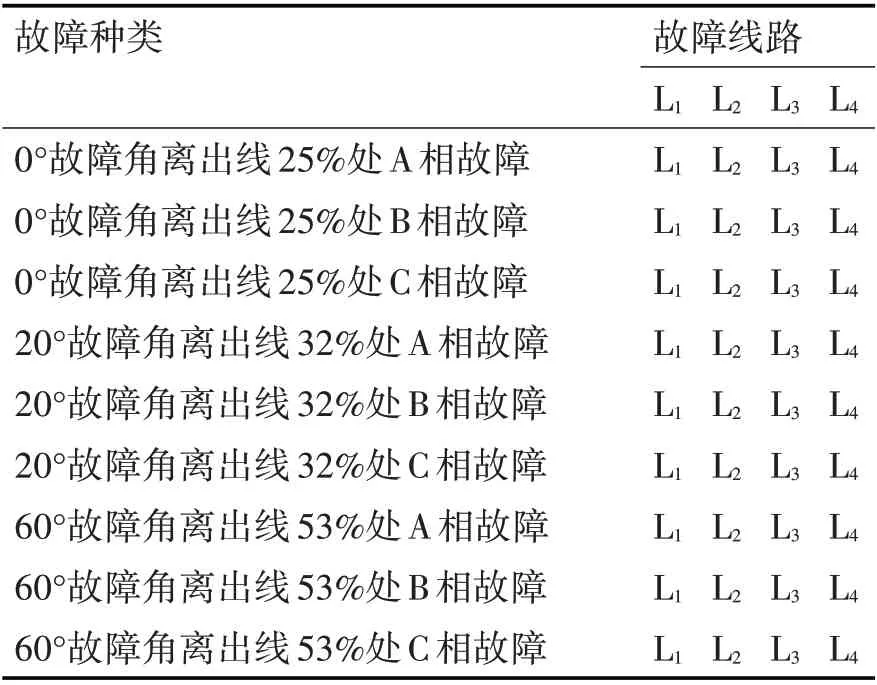
表1 同情况故障选线
6 结语
结合了EEMD-多尺度排列熵-SVM算法完成了小电流系统单相接地故障选线,EEMD算法抑制了模态混淆问题,消除了零序电流的噪声和干扰,通过计算多尺度排列熵,得到SVM的输入,通过SVM输出的标签作为故障判据完成故障选线,经仿真实验表明方法准确、简单,没有出现误判。
