基于ARIMA与线性回归组合模型的汽车销量预测分析*
2021-09-15桂思思徐晓锋
桂思思 孙 伟 徐晓锋
(1.武汉智慧生态科技投资有限公司 武汉 430119)(2.神龙汽车有限公司 武汉 430056)(3.武汉昱升光器件有限公司 武汉 430073)
1 引言
随着汽车的逐渐普及,汽车在人们的出行消费中占有越来越重要的地位,而汽车行业的飞速发展与激烈竞争,也给各个品牌的主机厂提出了更高的要求,实时掌握品牌未来的汽车销量,能够更好按需安排生产计划,控制汽车库存量,更能有效地为市场部门提供有针对性的营销数据支撑。
我们可以在各类文献中找到关于汽车销量的预测模型研究,如文献[1]基于汽车市场的月度销量进行中长期预测,提出了基于结构关系识别的汽车销量预测方法。文献[2]分析了我国汽车销量的主要影响因素,如经济环境、汽车价格、基础设施环境等因素,并计算出各影响因素的灰色关联分析,提出了基于回归分析的汽车销量预测模型。文献[3]根据我国汽车市场的月度销量数据,并基于具有季节调整的ARIMA进行汽车销量预测。
笔者进行调研发现,各类预测模型并未在各品牌的汽车主机厂得到广泛应用,分析原因主要为:1)主机厂更关注于面向单品牌的汽车销量预测,而现有预测模型大都根据汽车市场的总体情况,分析汽车行业的宏观影响因素进行建模,与面向单品牌的销量预测影响因素存在差异;2)部分模型选取的预测数据对主机厂来说比较难以获取,如有些模型需要统计全国公路里程,有些涉及品牌情感因素的分析需要抓取外部网站的数据。本文根据主机厂的数据现状,分析面向品牌汽车销量预测的主要因素,提出一种基于ARIMA与线性回归组合模型的单品牌汽车销量预测模型的建立方法。
2 影响因素分析
在汽车行业,面向普通大众的单品牌汽车销售流程大体为
1)单品牌的销售线索搜集。主机厂从各大垂直网站、自媒体、以及进4S店的用户登记数据获取销售线索,销售线索记录的往往是有购车意向的客户信息。
2)对销售线索进行跟进。这个过程主要是销售人员和客户进行沟通,跟进、价格谈判等。
3)销售线索的成交。销售线索成交后将转化为销售订单,也就是普遍意义上的汽车销售。
从上述流程流程中可以看出,销售线索是影响汽车销售的一个重要因素,也是汽车品牌主机厂真正掌握的售前数据之一。另外,普通的单品牌汽车销售会受到近期或去年同期销售情况的影响,因此历史销量也是进行销量预测的另一重要指标。下文中我们根据某汽车品牌提供的2014年~2018年销售线索及历史销量数据,对影响因素进行具体分析与建模。
3 预测模型建立
3.1 模型建立方法
模型的建立方法如下四步。
步骤1提取相关因素。检验相关因素的相关性,提取相关性较高的相关因素作为多元线性回归的自变量。
步骤2提取自回归自变量。建立自回归序列,对序列进行差分,并根据自相关和偏相关参数进一步对ARIMA模型定阶。
步骤3结合步骤1和步骤2提取的自变量建立多元线性回归模型。
步骤4对模型进行拟合、验证及调整,对各参数显著性进行检验,得到较完备的最终模型。
3.2 线性回归模型建立
回归分析是研究一个变量关于另一些变量的具体依赖关系的计算方法和理论,根据自变量的变化来预测因变量的变化,变化关系一般为相关关系,是统计学中一个常用的方法,被广泛地应用于社会经济现象变量之间的影响因素和关联的研究。
通过R语言将该品牌的销售线索数据与销量数据进行相关因素分析,计算Pearson相关系数为0.8052126,可以看出该品牌的销售线索与汽车销量之间的相关性很高。建立以销售线索Xi为自变量,销量Yi为因变量的线性回归模型如下
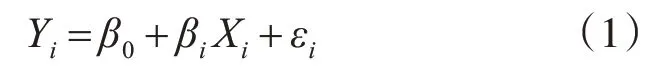
上式中β0为截距项,βi为模型的参数,误差项εi是随机变量。
3.3 ARIMA模型建立
该品牌汽车销量的月度数据具有长期趋势、季节变动,随机波动的特点,我们选择通过自回归模型进行分析,自回归模型被广泛地应用于包含销量预测在内的时间序列的分析与预测中。
ARIMA模型是对非平稳时间序列进行分析的方法,在对序列进行差分后建立自回归移动平均模型,季节性的ARIMA模型是在ARIMA模型的基础上加入了季节的考虑而改进的模型,假设对于Yt的随机时间序列,经过d阶差分后为平稳序列,模型满足如下模型结构:
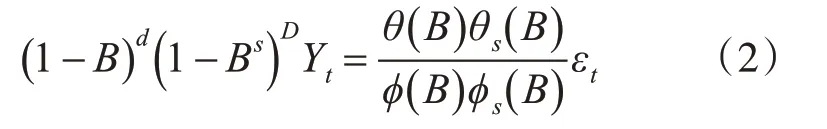
其中B为延迟算子,有BpYt=Yt-p,误差项是当期的随机干扰εt,为零均值白噪声序列。其中:

称该模型为AR IM A(p,d,q)(P,D,Q) m
首先建立该品牌以月为单位的销量数据的原始序列Yt,t=1,2,3,…对销量数据进行平稳性检查,时序图如图1,可以看出时序图有明显的递减趋势,单位根检验统计量对应的p值为0.2904,显著大于0.05,该序列是非平稳序列,自相关图图2显示,自相关系数长期大于零,说明序列间有相关性。
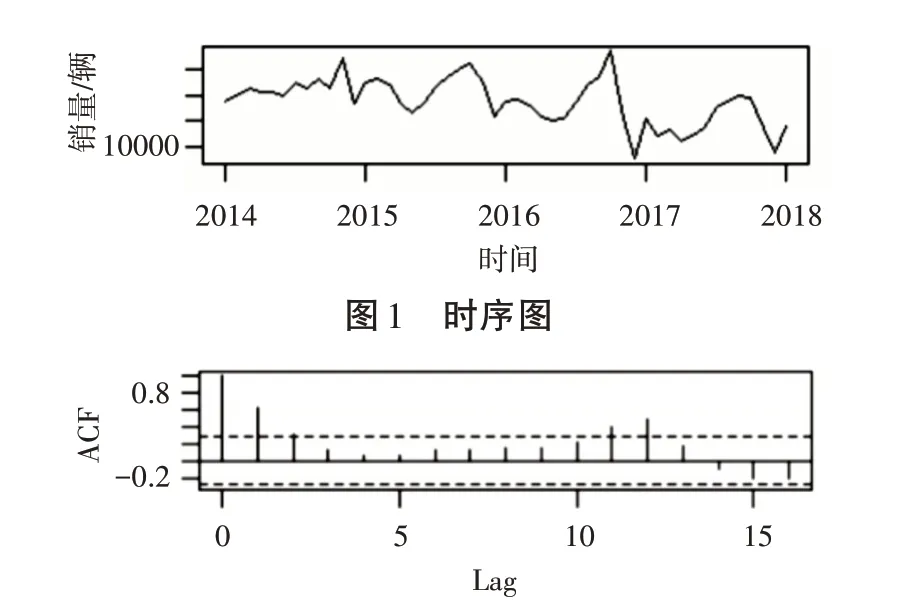
图2 自相关图
对序列进行一阶差分∇yt=∇yt-∇yt-1,如图3显示一阶差分之后序列的时序图在均值附近比较平稳的波动,进行单位根检验,p值为0.01,表明一阶差分之后序列是平稳的。

图3 一阶差分时序图
对一阶差分后的序列进行自相关和偏相关判断如图4和图5,从自相关图和偏自相关图可以看出,acf拖尾,pacf截尾,并且可以看出lag值延迟12阶处,自相关和偏自相关系数都显著非零,说明一阶差分后序列具有季节效应。
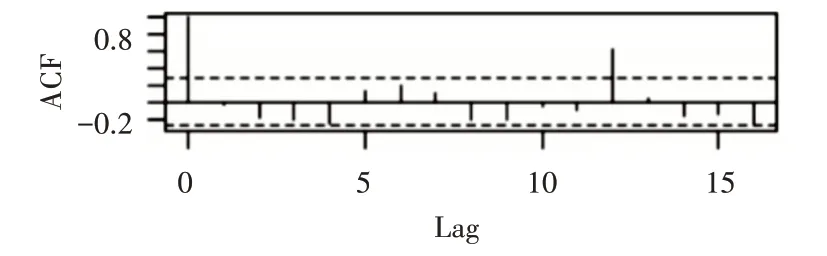
图4 一阶差分自相关图
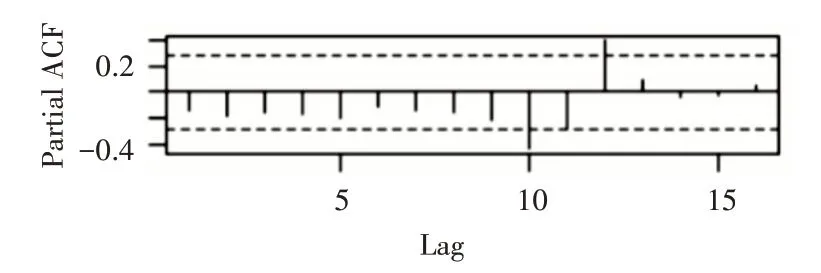
图5 一阶差分偏自相关图
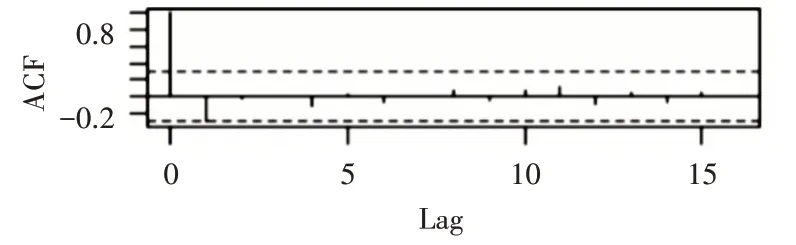
图6 两次差分后自相关图
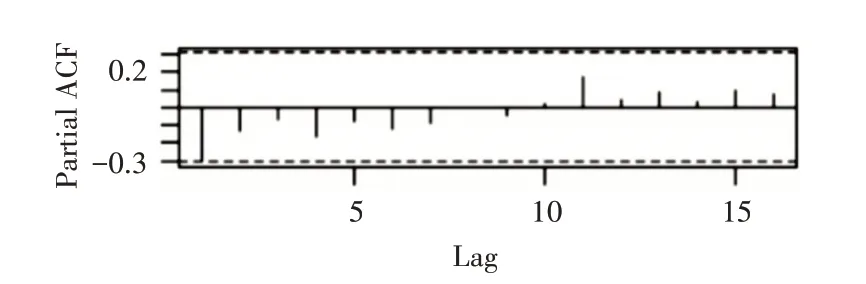
图7 两次差分后偏相关图
将ARIMA(1,1,0)(0,1,0)12模型各值带入到式(2)中,可得该品牌基于历史销量的时间序列表达式为
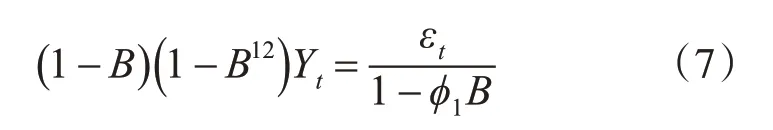
3.4 模型组合
自回归模型本身就是多元线性回归模型的一种,通过式(3)可以确认t时刻的随机变量Yt是Yt-1、Yt-2、Yt-12、Yt-13、Yt-14的多元线性回归。因此将上述自变量结合式(1),形成多元线性回归方程(8),如下:

β0为截距项,β1~β6为模型的参数,Xt为t时刻销售线索,Yt-1、Yt-2、Yt-12、Yt-13、Yt-14为对应t-1、t-2、t-12、t-13、t-14时刻的历史销售数据,误差项εt为t时刻随机变量。
4 模型验证与调整
通过R语言进行模型验证及参数调整,首先验证只有销售线索变量的模型,根据式(1)进行拟合优度检验,提取可决系数R2为0.5003,Rˉ2为0.4897,可以看出样本拟合度不高,根据式(8)对组合后的模型进行拟合度检验,提取可决系数R2为0.8288,Rˉ2为0.8043,可决系数明显提高,对模型进行单个变量的显著性检验,各项t检验的p值如表1,可以看出截距项的t检验结果为不显著。

表1 式(4)各变量的t检验p值
剔除截距项,得到式(9):
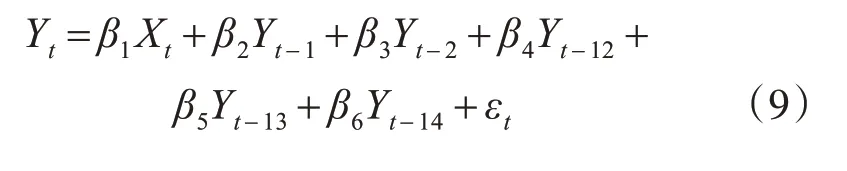
根据式(9)对进行拟合度检验,提取可决系数R2为0.9833,Rˉ2为0.981,可决系数进一步提高,对模型进行单个变量的显著性检验,各项t检验的p值如表2,均小于0.05,模型整体显著性检验F检验统计量为421.8,两个自由度为6和43,对应的检验P值为2.2e-16,说明模型整体是显著的。
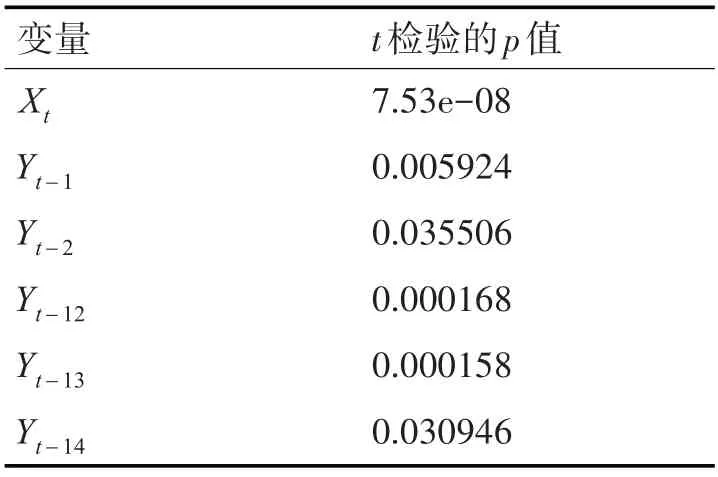
表2 式(5)各变量的t检验p值
根据该模型预测值的百分比误差RPE如表3。其中RPE计算公式如式(10),其中y^t为t时刻预测值,yt真实值。


表3 预测值的百分比误差
5 结语
该模型在对2018年4月~2018年11月的销量预测中,除了7月RPE值较大,其他预测偏差均在8%以内,预测效果较为理想,证明了该模型建立方法的可行性。
销售线索及历史销量数据是影响单品牌销量预测的重要因素,在模型的建立过程中不可相同对待,销售线索与销量密切相关,可直接作为线性回归模型的因变量处理,而历史销量具有趋势性和季节性的特点对销量预测的影响更加复杂,因此需要通过非平稳时间序列的分析进行模型因变量的提取,最后再将各个因变量进行模型组合。整个模型建立过程中线性回归模型是建模的基础模型,各个因变量的提取是模型建立的关键。本文提出建模思路及方法符合大多数汽车品牌的数据基础,较易实现,可为面向单品牌的汽车销量预测提供参考。
