基于改进PSO与规则约简的模糊系统优化算法*

蔡际杰 陈德旺 黄允浒 黄 玮

（1.福州大学数学与计算机科学学院 福州 350108）

（2.福州大学智慧地铁福建省高校重点实验室 福州 350108）

（3.福州理工学院计算与信息科学学院 福州 350506）

1 引言

模糊系统（Fuzzy System，FS）在二十世纪90年代初期间发展迅速，尤其是在模糊控制领域的应用效果突出［1］。但是近年来FS的研究并非主流，究其原因主要是因为目前FS的研究还不够成熟［2］，主要表现在隶属度函数类型和参数的选择主要依靠经验、现有FS的适用范围有限、缺乏在通用硬件平台中的实现方法等［3］。WM（Wang-Mendel）算法［4］简单、实用，已经成为了FS研究领域的经典方法，但该算法也同样存在上述问题。尽管近年来许多学者根据这些问题提出了一些改进的办法，但是这些改进方法仍存在计算复杂、改进效果不明显以及优化目标不全面等问题。

文献［5］针对WM算法存在的问题，利用采样数据挖掘技术完成了进一步的改进，但该方法在规则库的鲁棒性上仍然有待提高；文献［6］提出了一种基于优化模糊规则输出集合中心的改进WM方法，提高了WM方法的鲁棒性和模型精度，但该方法难以应对高维问题。近年来，利用遗传算法［7］与进化算法［8］优化FS的改进方法也相继被提出，但由于计算过于复杂，因此难以真正应用在FS的优化中。文献［9］通过遗传算法和梯度下降法对FS的结构和参数进行了优化，取得了较好的效果，但是其模型复杂度过高，不易求解。而后许多学者开始利用高效、简单的PSO算法对FS模型进行优化，如文献［10］提出了一种基于PSO算法的WM方法，该方法通过改进的PSO算法对数据覆盖区域的模糊规则质心进行优化，再利用外推得到完整的模糊规则库，一定程度上提高了WM方法的预测精度，但其规则数随输入呈指数增加，算法效率急剧下降；文献［11］为提高FS模型的预测精度，利用ANFIS、GA算法和PSO算法对模型的隶属度函数范围进行了优化，进一步提高了模型的预测精度，但未进一步研究模糊规则的约简。

针对以上问题，可以发现目前FS的优化仍然存在很大的进步空间。目前的优化研究主要是针对FS模型的精度方向改进，而在规则约简方面的研究较为欠缺，规则约简后的优化模型是否仍可以保证模型精度的提高仍需进一步考察；且FS隶属度函数主要是针对三角形隶属度函数，而由高斯型隶属度函数构成的FS研究相对较少。由此可见亟需一种在规则约简的条件下，既能够保证模型可解释性又能够保证模型精度的FS优化算法。

因此，本文致力于提高FS模型的精度和约简模糊规则。通过改进PSO算法对具有高斯型隶属度函数的FS进行有效优化，提出了CPSFS和SPSFS两种模糊系统优化算法。实验结果表明本文提出的CPSFS算法在约简大量模糊规则后，依然能够保证训练集和测试集上的预测精度领先于传统的BP神经网络、RBF神经网络等回归算法，具有很好的发展前景。

2 模糊系统构造

构造FS模型首先需要划分模糊区间，设置每维变量的模糊集合个数；然后初始化模糊区间中每个模糊集合对应的隶属度函数参数，对训练集数据的每维变量做模糊化处理，模糊化后的变量属于模糊值最大的模糊集合。完成模糊化操作后，可根据每条数据对应的模糊集合组合产生IF-THEN规则，对m维输入n维输出的IF-THEN规则表示如下：

I F(x1is Ap1and…and xi is Api)

T HEN(y1is Bq1and…and yj is Bqj)

(i=1，2…m，j=1，2…n)

其中pi为第i维输入变量划分的模糊集合个数，qj为第j维输出变量划分的模糊集合个数。本文采用的隶属度函数为高斯型隶属函数，其定义如下：

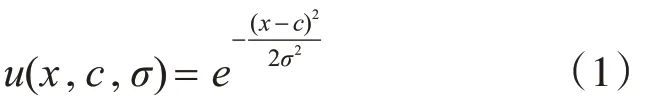
其中x为变量值，c为隶属度函数的中心值，σ为隶属度函数的方差。

按照上述方式，若每条数据对应产生一条规则，那么当数据量增大到一定程度时，将生成非常多的模糊规则，导致FS模型越来越复杂，无法保证其可解释性。且按此方式生成的规则库包含大量的重复规则、冲突规则和无法真正体现数据特点的“坏规则”，因此需要对这些“问题规则”进行消除操作。本文通过计算每条规则的支持度，筛选掉支持度较小的规则，从而达到约简规则的目的。由最终保留的规则组合形成FS规则库，代入FS的结构即可完成模型的构建。对m维输入n维输出的数据产生的规则，其支持度（SD）计算方式如下：

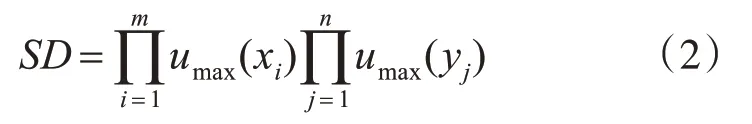
本文采用的FS为带有乘积推理机、单值模糊器、中心平均解模糊器和高斯型隶属度函数的模糊系统，其形式如下：

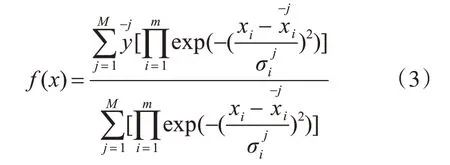
3 粒子群优化算法

粒子群优化算法最早由Kennedy和Eberhart提出［12］，其核心就是每个个体会在每次迭代中通过跟踪个体当前最优值pb esti和群体最优值gbest更新自己的位置和速度［13］，规定迭代次数完成后，群体发现的最优位置gbest即为最优解。其位置和速度更新公式如下所示：

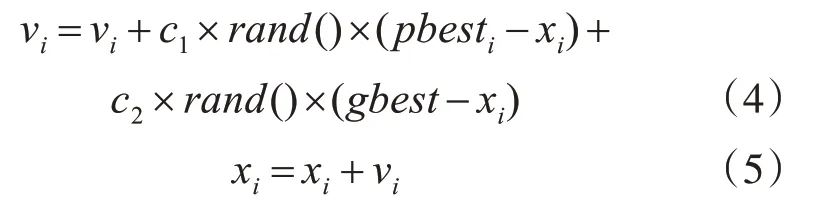
其中i=1，2，……N，N为群体中粒子的总数，vi为粒子i的速度，xi为粒子i的位置，c1，c2表示学习因子。

3.1 标准粒子群优化算法

Shi等［14］发现式（4）中的第一部分vi本身具有随机性，为了扩大搜索空间，在vi前乘以惯性权重w来增强算法的搜索能力，提出了一种标准PSO算法（SPSO），其速度和位置更新公式如下：

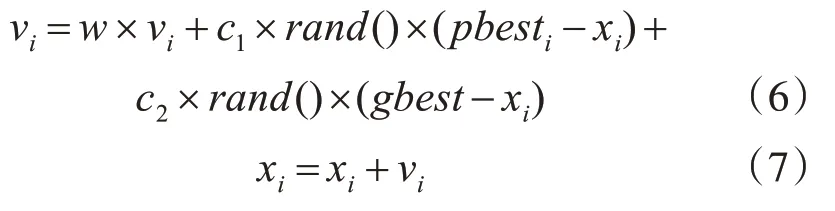
3.2 基于收敛因子的粒子群优化算法

Clerc等［15］为加快PSO算法的收敛速度，在（6）式中引入了收敛因子K，提出了一种基于收敛因子的PSO算法（CPSO），其速度更新公式如下：

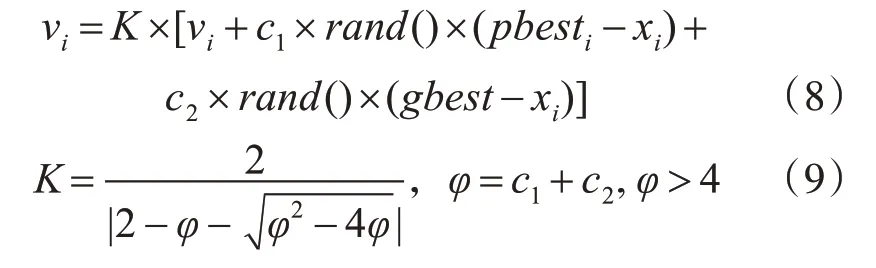
通常将φ设为4.1，则K由式（9）计算后为0.729。

4 本文方法

目前FS隶属度函数的参数选取主要是依靠经验，选取的参数很有可能并不适合当前的数据，导致生成的FS模型效果很难达到最优。因此本文利用SPSO算法和CPSO算法对FS的隶属度函数的参数进行了优化。通过寻找隶属度函数的最优参数达到优化FS模型的目标。利用SPSO算法优化后形成的FS优化算法称之为SPSFS算法，利用CPSO算法优化后形成的FS优化算法称之为CPSFS算法。

PSO算法具体的初始化操作是选取粒子数量N、设定粒子空间维度dim以及优化的迭代次数max_iter，迭代次数应该保证模型能够在迭代次数范围内寻找到隶属度函数参数的最优值。为扩大搜索空间，本文粒子个体数设为30，迭代次数设为100次。为了将上述PSO算法应用在FS的优化中，本文将每个粒子的位置初始化为每维变量对应模糊集合的隶属度函数参数（即高斯隶属度函数中的中心值c和方差值σ），将每个粒子的适应度值设置为模型的目标函数值，即FS模型的均方误差指标MSE。若粒子当前所处位置的适应度值在当前迭代次数中最小，则可以将其位置设置为该个体目前寻找到的最优位置pb esti，若粒子所处最优位置在整个群体中取得的适应度值最小，则可以将其位置设置为整个群体目前寻找到的最优位置gbest。

规定迭代次数完成后，群体寻找到的最优位置gbest即为FS高斯隶属度函数的最优参数，将最优参数代入到FS模型中每维变量对应的隶属度函数中，按照FS的常规流程建模，所产生的模型效果即可达到最优。

利用PSO算法优化FS模型的流程如图1所示。

图1 本文算法流程图

5 实验结果及分析

为了更直观地对CPSFS算法和SPSFS算法进行评价，本文引入了传统的BP神经网络算法、RBF神经网络算法、LR线性回归算法以及WM算法。同时，引入平均绝对误差（MAE）、均方误差（MSE）以及决定系数R2作为算法的评价性能指标，其定义分别如下：

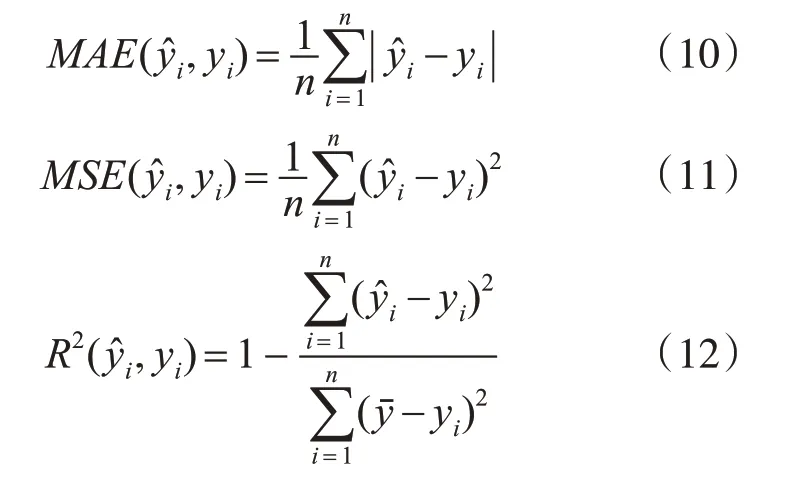
5.1 数据集描述

表1描述了本实验采用的数据集的具体属性。1号数据集为预测房价数据集；2号数据集为预测广告投资收益数据集。实验中按一定比例将每个数据集随机划分为训练集和测试集。

表1 实验数据集信息

5.2 RES数据集应用

各算法在训练集上的预测效果如图2所示，在测试集上的预测效果如图3所示，表2展示了各个算法预测训练集的各项性能指标，表3展示了各个算法预测测试集的各项性能指标。

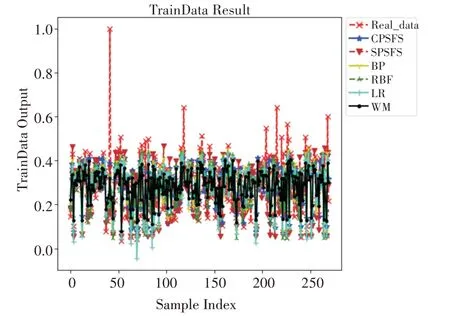
图2 RES训练集预测效果

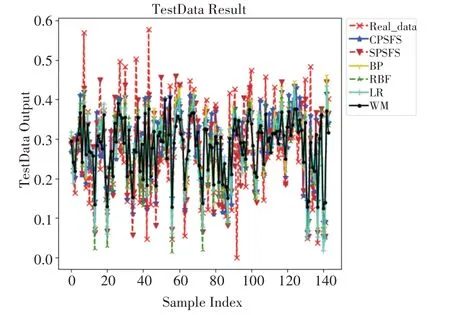
图3 RES测试集预测效果

如表2和表3所示，可以发现CPSFS算法在训练集与测试集上占主要优势，各项评价指标上均优于其他经典算法。以表3为例，CPSFS算法在MSE指标上：相比BP下降了5.2%，相比RBF下降了8.2%，相比LR下降了18.4%，相比WM下降了14.6%。同时，CPSFS算法和SPSFS算法均降低了模糊规则数，但相比CPSFS算法而言，SPSFS算法的综合表现并没有很好。尽管SPSFS算法降低的规则数更多，但是该算法无法保证降低规则数后各项评价指标领先于其他经典算法，而CPSFS算法既可以降低规则数，又能够保证预测评价指标最好。传统的WM算法产生了729条规则，规则数太多，模糊规则库更加复杂，导致可解释性变差；而CPSFS算法生成的规则数仅103条，相比WM算法一共减少了626条，模糊规则库复杂度大大降低，人们可以快速地从较少的模糊规则中理解模型结果的产生依据，从而更有效地保证了算法的可解释性。

表2 RES训练集预测评价指标

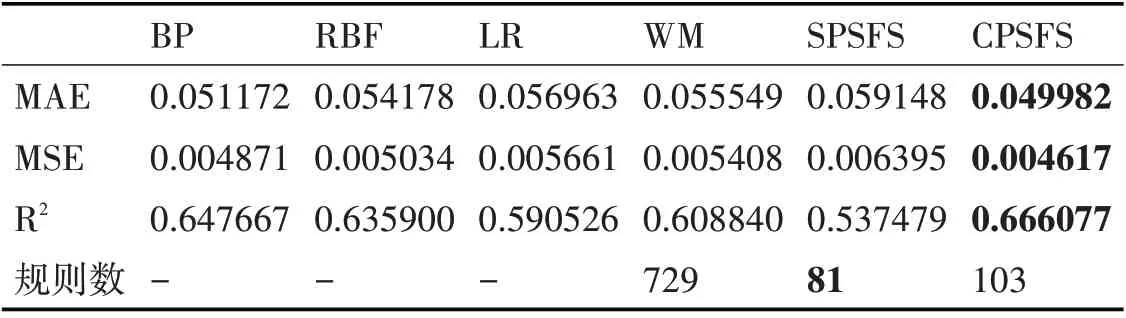
表3 RES测试集预测评价指标

5.3 ADV数据集应用

各算法在训练集上的预测效果如图4所示，在测试集上的预测效果如图5所示，表4展示了各个算法预测训练集的各项性能指标，表5展示了各个算法预测测试集的各项性能指标。

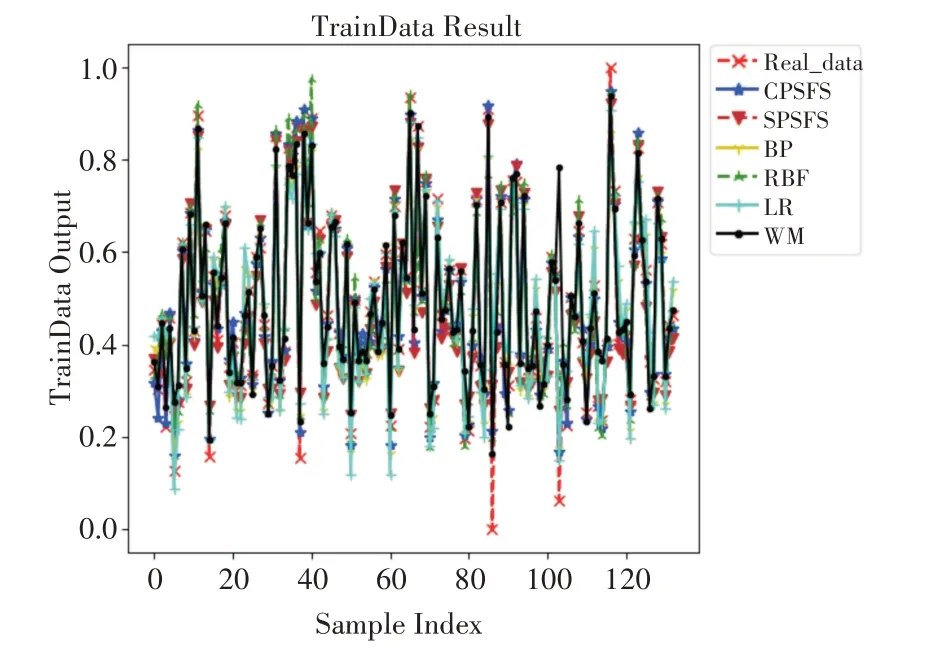
图4 ADV训练集预测效果

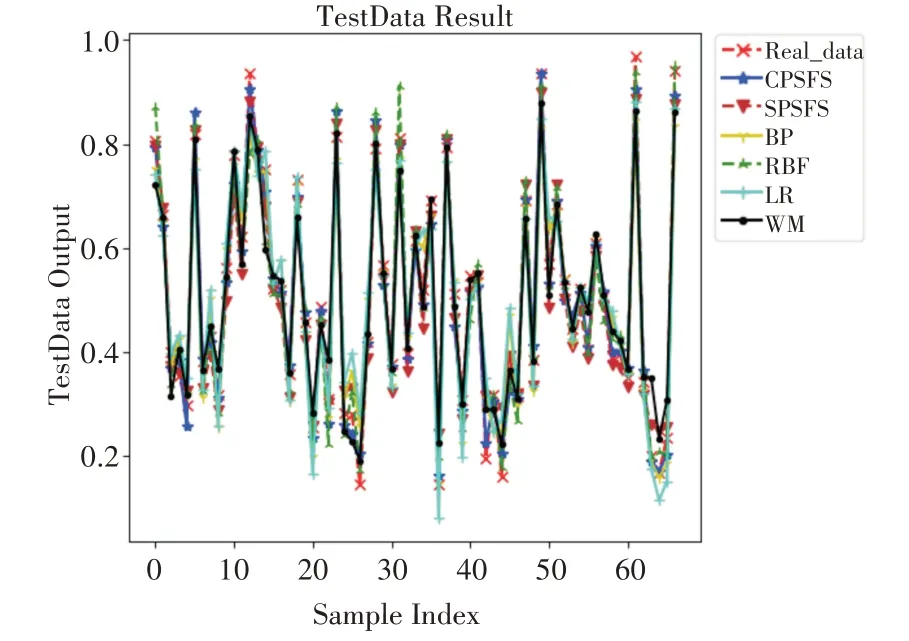
图5 ADV测试集预测效果

如表4和表5所示，可以发现CPSFS算法在训练集和测试集中依然占主要优势，其各项评价指标均优于BP、RBF等经典算法。以表5为例，CPSFS在MSE指标上：相比BP、RBF、LR和WM分别下降了70.0%，59.5%，77.1%和63.5%。在规则数上，尽管SPSFS算法减少了大量模糊规则，但其无法保证精度最优；而CPSFS算法则具有这个优势，在降低规则数的条件下依然保证精度领先，其生成的规则数比传统的WM算法更少，一共约简了90条规则，一定程度上保证了模型的可解释性。

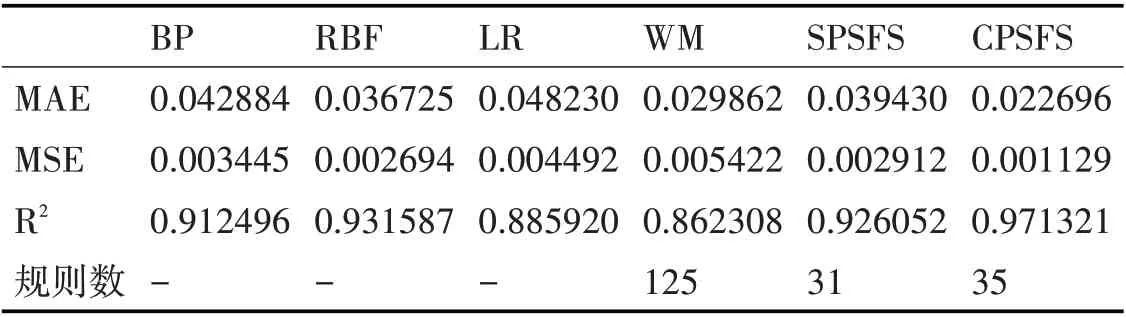
表4 ADV训练集预测评价指标

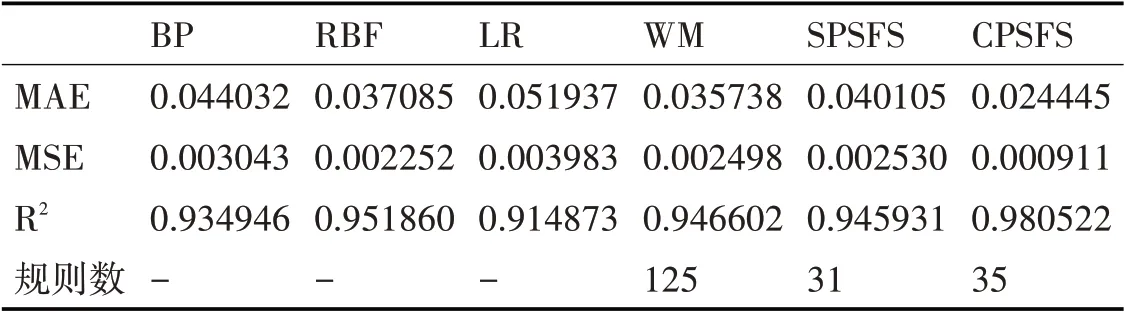
表5 ADV测试集预测评价指标

6 结语

本文针对FS目前精度不高、规则数太多、无法保证收敛速度等问题，通过SPSO算法和CPSO算法对具有高斯型隶属度函数的FS进行了优化。通过SPSO算法优化形成的SPSFS算法虽然降低了规则数，但却无法保证回归精度最优；而通过CPSO算法优化所形成的CPSFS算法在回归任务上均取得了不错的效果，在训练集、测试集上的各项评价指标均优于传统的回归算法。且在优化后，CPSFS算法产生的规则数大大降低，有效地保证了其可解释性在各个经典算法中居于首位。

综上所述，本文提出的CPSFS算法不仅具有较强的可解释性，而且在回归问题上的表现优异，能够有效解决相对低维的回归问题。后续的工作中将会考虑搭建多层模糊系统来提高算法应对高维数据的能力。相信通过广大学者的不断努力以及FS的可解释性优势，在不久后的将来，FS的应用领域将会更加广泛，并成为深度学习下具有独特优势的AI技术。