小样本条件下装备作战效能评估问题研究*

张家宾

（91404部队 秦皇岛 066000）

1 引言

在武器装备发展建设过程中，装备性能试验的测试及评估分析对于装备的改进、提升及指导部队的作战使用都具有重大意义。作战效能评估一般指武器装备在相应的作战背景下，针对具体的作战对手构建近似于实战的、逼真的试验环境，综合进行作战能力的评估。评估结果可以识别并评估装备的设计和使用缺陷，为新装备作战使用提出建议，为装备的列装定型提供决策，同时在装备的作战适用性、体系贡献率和作战效能方面给出结论。作战效能的评估方法众多，包括层次分析法、ADC法、指数法等，每种方法均需要构建作战能力指标体系并将指标定量化。对能力指标的定量化需要基础数据做支撑，但长期以来由于兵力短缺、靶标保障困难、复杂环境难以构设等因素限制，作战效能评估一直面临着样本量不足的问题。通过一次或少量几次试验也很难获得一些复杂环境、边界条件下的试验数据，无法用概率统计的方法进行试验结果的评估。针对上述问题，一般根据原始数据或小样本的数据特征扩充样本量，在大的数据基础上再进行后续能力特征分析。

对于处理小样本数据条件下的能力特征问题，工程上已经有很长的应用经验。传统的数据样本量扩充方法按是否存在先验信息即了解数据的统计规律信息大致分为两类。对于有先验信息的数据样本可以采用Bayes方法扩充样本量。对于不了解数据特征规律的样本量，一般选用Bootstrap方法来扩充样本量［1］。由于作战试验获取的数据多为无统计规律的数据，文章采用的是Bootstrap方法进行样本量扩充，下面介绍其基本数学原理，并针对存在的适用性问题引入改进的Bootstrap方法。

2 两种样本量扩充方法的数学原理

2.1 Bootstrap方法

Bootstrap方法是一个传统小样本量扩充方法，该方法为一个再抽样过程，通常也称为计算机增强型统计推断过程。该方法是在小样本分析中经常使用该方法，其基本原理通过数理统计方法构建基于现有小样本数据的统计分布，对样本的统计分布规律参数进行评估，将小样本问题转化为大样本问题，其一般步骤如下［2～3］。

取试验中所得原始试验数据样本序列为X=(x1，x2，…，xn)，该样本数据量有限，我们称该样本为原始样本。

令xi～F(x)，i=1，2，…，n，

F(x)为经验分布函数。

由这些原始样本构造的经验分布函数一般形式如下：

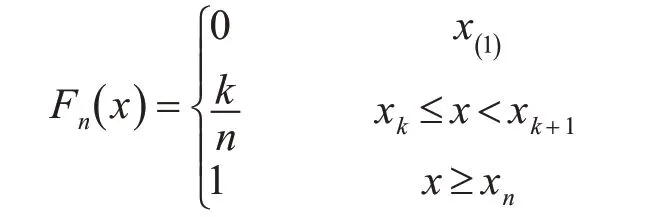
其中，x(1)≤x(2)≤…≤xn是一组顺序统计量，是x1，x2…，xn按从小到大排列后得到的数据序列。

利用上述经验分布函数Fn来构造N组新的样本数据，即抽取新的试验样本，方法如下：

取区间为0～M（M≫n），η为计算机产生的随机数（η取整数且具有独立性、均匀性）。

令i=η%n，

在观测值中找到对应下标为i的样本xi作为新生成样本x*，则x*为所需的新的随机样本序列值。

这N组新样本为

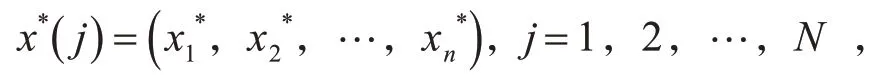
我们称这些样本为自助样本。

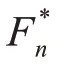
引入Rn如下：

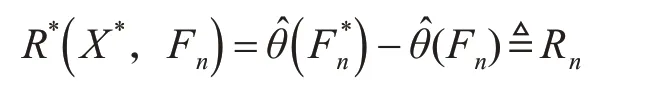
Θ为样本分布的特征值，θ^为特征值估计。由于根据小样本试验很难求出θ(F)，上式中用θ^(F)近似代替θ(F)。

Bootstrap方法是通过构造经验分布函数，再利用随机数挑选构建新的样本序列。对新构建的统计序列进行参数估计，积累参数估计的值，统计参数的分布规律进而得到样本的参数估计值。该方法原理清晰，计算步骤简单，是实际的样本数据扩充中经常用到的方法，但由于该方法为样本的重复再抽样，所以导致所生成的自助样本中原样本点的重复率偏高，最终的参数估计不准确。针对该问题引入下面的Bayes Bootstrap方法。

2.2 Bayes Bootstrap方法

引入Bayes Bootstrap的数据生成方法，对上述Bootstrap的样本扩充方法进行部分改进，使得扩充后数据对原始样本点的重复率降低［5～9］。其数学原理如下。

设原始样本为X=( )x1，x2…，xn，该样本量是有限的，则利用Bayes Bootstrap方法生成自助样本的方法步骤如下。

取服从于Dirichlet分布的随机变量：

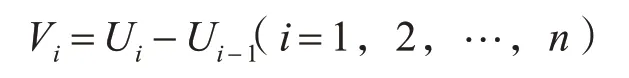
其中U0，U1，U2，…，Un-1为服从于（0，1）均匀分布的随机数，取U0=0，Un=1。

那么有

V1+V2+…+Vn=1

则该样本的平均值估计为

重复上述步骤，逐步得到均值和方差的平均值。

Bayes Bootstrap方法通过构造服从于Dirichlet分布的随机变量，使新生成样本为原始样本按随机概率生成，然后通过多次迭代来生成自助样本，使得新样本中原样本点出现率大大降低，一定程度上消除了新样本的偏向性特征，在样本数据扩充方面比改进前更有优势。

3 模型验证及效果对比分析

给出已知分布规律的小样本数据，利用上述两种方法模型分别进行数据样本扩充并计算分布特征的估计值，然后进行对比，分析两种方法的实际应用效果。

取服从于正态分布N（2，1）的样本数据列为（1.7586，2.3192，2.3129，1.1351，1.9699，1.8351，2.6277，3.0933，3.1093，1.1363）

利用Bootstrap方法扩充原始样本的数据量，若将数据扩充为100组，利用Matlab画出统计的直方图如图1所示。

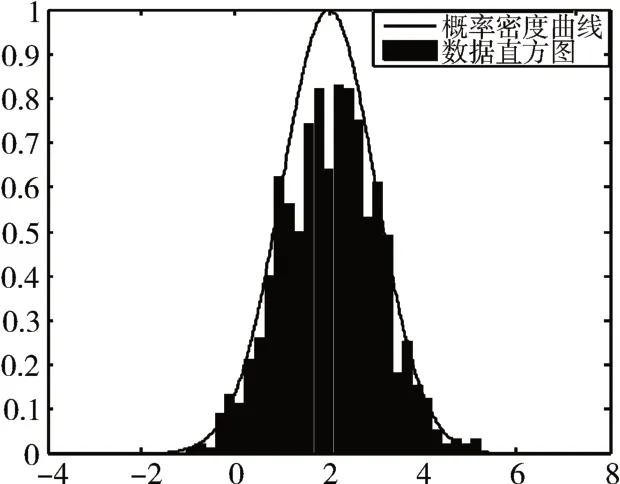
图1 自助样本统计特性验证图

从图上可以看出新生成的样本分布近似接近于原分布的特征。为进一步对比两者的参数估计效果。分别用Bootstrap、Bayes Bootstrap方法扩充原始样本生成自助样本，并对新样本做均值参数估计和区间估计，取0.95的置信度，计算结果如表1所示。

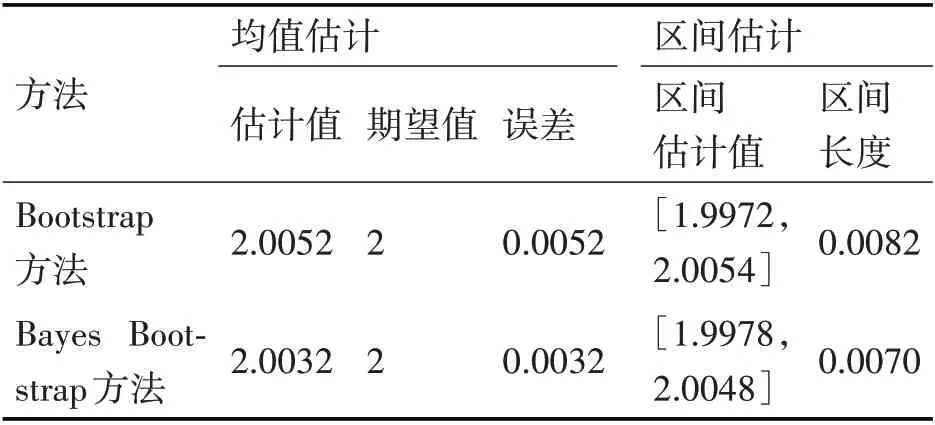
表1 两种方法所做参数估计和区间估计对比表

对比两种方法在对小样本数据的特征值估计方面的效果，两种方法产生的估计特征值和原始分布相比均值误差分别为0.0052、0.0032，区间估计长度分别为0.0082、0.0070。两种方法得到的误差值都在误差范围内，样本都服从相应参数下的正态分布，表明两种方法在对小样本条件下的参数估计都符合原分布特点。同等条件下，改进的Bayes Bootstrap方法比Bootstrap方法，均值参数估计误差更小，区间估计长度更短，表明改进的Bayes Bootstrap方法在小样本参数估计方面能更精确。这也验证了改进方法通过多次迭代生成的自助样本，使得新样本中原样本点出现率大大降低，从而使参数估计效果更有优势。

4 对空拦截能力作战效能评估研究

将Bayes Bootstrap方法应用于某舰艇参加作战试验鉴定时对空拦截能力的作战效能评估。由于试验成本、兵力短缺、环境构设复杂等因素限制，对空拦截试验数据采集不充分，为提高试验结果置信度、增加对空拦截能力考察的全面性并综合考评装备系统的效能，考虑通过Bayes Bootstrap方法扩充样本量，在大样本量下进行数据分析及参数估计，迭代若干次参数估计的数值后取平均值来确定最终的参数值。

对空拦截的作战效能评估应首先构建对空拦截作战能力指标体系。体系的建立应以舰艇的使命任务为牵引，从装备的性能指标出发，综合考虑作战样式、作战对手及作战环境等因素。结合本舰性能特征分析上述因素后，从舰艇对空信息感知、指挥控制、打击概率、毁伤效果等方面进行考虑［10～12］，构建该型水面舰艇能力指标如图2所示。

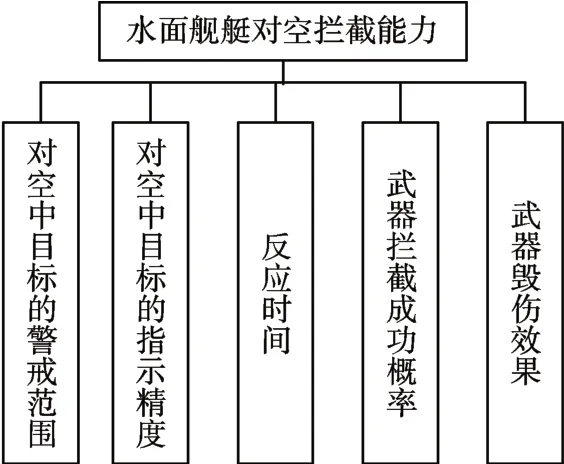
图2 对空能力指标图

作战效能评估可以采用指数评估法、层次分析法、ADC法等，此次评估采用最常用的指数法。该方法首先需对评估体系中的各项指标进行量化，然后进行各指标间的权重分配计算，最后进行指标权重的加权和确定最终的评估值。

以上述指标中的精度指标为例，将对空探测距离精度值（RMS）按距离分段，在不同航次的同一距离段，对测量值和真值进行数据处理获得在各个航次下，探测距离精度值如下：

（0.05，0.06，0.08，0.03，0.10，0.07，0.05）

考虑到能力指标的正比例关系，对精度值进行正比例处理得到：

（0.95，0.94，0.92，0.97，0.90，0.93，0.95）

利用上述的Bayes Bootstrap方法对精度样本进行扩充并分析精度样本的特征值。

原始样本数据为

X=(x1，x2…，xn)=(0.95，0.94，0.92，0.97，0.90，0.93，0.95)

取服从于（0，1）均匀分布的随机数序列U0，U1，U2，…，Un-1为

（0，0.13，0.22，0.38，0.55，0.62，0.70，0.91，1）

那么有服从于Dirichlet分布的随机变量

V1，V2，…，Vn=Ui-Ui-1=(0.13，0.09，0.16，0.17，0.07，0.08，0.21，0.09)

满足：

V1+V2+…+Vn=1

计算该样本的平均值参数估计为

样本方差估计为

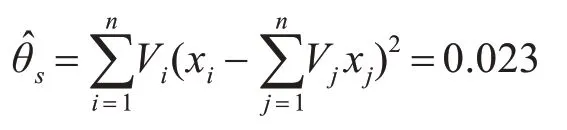
重复上述步骤五次，进行迭代，最终得到平均值和方差值的估计值见表2。

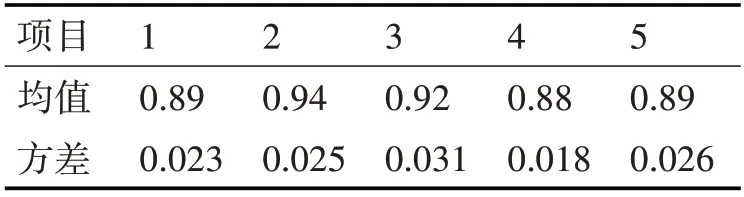
表2 五次平均值和方差迭代表

对五组数据取平均值后最终的均值和方差的为

同理，根据上述方法可以得到对空拦截能力指标体系内其他指标经Bayes Bootstrap方法处理后得到的估计值，令计算得到的各指标能力值为Ki（其中i为指标个数）。指数法进行作战效能评估还需要进行各指标权重的计算，一般利用专家打分法确定体系内各指标的权重ωi并经过判断矩阵检验其一致性，则该型水面舰艇最终的作战效能评估结果为

评估结果是在相应作战背景下，对作战对手的能力评价，对部队有针对性的改进战法、提高训练效果具有重要的指导意义。

5 结语

针对作战效能评估处理中一直存在的样本量不足的问题，文章对比了传统的Bootstrap和改进的Bayes Bootstrap样本扩充方法，验证了Bayes Bootstrap方法在参数估计和区间估计方面的精确性，并将该方法成功应用于某型舰艇的对空拦截能力的作战效能评估中，提高了结果的置信度。但该模型并不能应用于成败型试验（即10问题）的效能评估，而该类试验往往为导弹射击等高消耗试验，对其作战效能评估具有重大的参考意义，这也是下一步要研究的方向。