流凌条件下弯道水力特性数值模拟

2021-09-14李民康冀鸿兰罗红春郜国明张宝森

水利水电科技进展 2021年3期

李民康，冀鸿兰，罗红春，郜国明，张宝森

(1.内蒙古农业大学水利与土木建筑工程学院，内蒙古呼和浩特 010018； 2.黄河水利科学研究院国际合作与科技局，河南郑州 450003；3.黄河水利科学研究院防汛抢险技术研究所，河南郑州 450003)

封冻期河冰演变过程包括成冰、流凌、初封、稳封、融冰、开河过程，冰花的迁移贯穿在整个封冻期，是河冰变化过程中不可或缺的一部分[1]，冰在水体中随水流流动称为流凌，可分为封冻前结冰流凌和开河期解冻流凌，前者以冰花为主，后者以碎冰为主。流凌的输移演变改变了河道边界条件和水力特征，河道堆冰容易形成冰塞冰坝，在弯道险工处尤为明显，冰塞冰坝引起过流断面减小，壅高上游水位，易形成凌汛险情。在数值模拟分析领域，目前对流凌和水内冰的研究颇具代表性。茅泽育等[2-3]采用河道冰水耦合模型及垂向二维紊流模型，对天然河道冰塞、水内冰演变、河冰过程等进行了模拟；樊霖等[4]根据冰/水力学、热力学建立数值模型模拟伊丹河封冻期冰情演变；王军等[5]基于多相流理论，对流体相和颗粒相建立数学模型，得到冰颗粒的迁移规律；李超等[6]基于二维DynaRICE河冰模型对三湖河口弯道水力特性及卡冰过程进行数值模拟，并分析了弯道卡冰机理；Shen[7]利用SPH法模拟河冰二维运动，在RICE和DynaRICE模型的基础上改进了河冰模拟系统CRISSP，可模拟冰塞演变及冰颗粒迁移等河冰过程；倪宝玉等[8]利用FLUENT模拟了波浪与冰的耦合作用，获得了多浮冰耦合效应；金占军[9]利用RNGk-ε湍流模型和流体体积法(Volume of fluid，VOF)方法，对冰水两相流浮冰受力、冰水两相流中浮冰的翻转下潜进行了研究；冀鸿兰等[10]基于可变模糊聚类循环迭代模型对流凌的输移发展进行分析，预报了巴彦高勒站流凌日期；张莹[11]利用PIV实验研究与SPH数模结合的方法对单/双颗粒流场特性进行了研究；刘寒秋等[12]通过欧拉-拉格朗日双向耦合法，对冰晶影响下的管道冲蚀磨损进行了研究；邓义斌等[13]研究了冰水两相流在不同因素影响下的管道阻力特性，对冰水两相流动的阻力特性进行数值模拟研究；王晓玲等[14]建立了三维非稳态欧拉两相流模型，模拟分析了不同转弯半径对弯道排冰的影响；姜坤[15]利用弯道水槽，基于FLUENT-EDEM耦合的三维两相流数值模型，对冰颗粒的输移特性进行了研究。

以上研究主要是利用各类方法对冰水两相流的内在机制进行探讨，或在特定约束条件(弯道)下进行冰水耦合运动的分析。然而，弯道几何特性如曲率半径、弯曲度、宽深比等，对水流结构、泥沙输移及多相流耦合过程有着重要影响，其中，吴新宇等[16]以若尔盖盆地实测资料为基础，建立水动力数学模型，分析了弯曲河流颈口裁弯过程中的水流运动特性。然而在流凌条件下，弯道几何特性的研究还需进一步深入。本文利用VOF技术，采用RNGk-ε湍流模型，对弯道几何特性中的弯曲度进行建模分析，利用CAD构建4种典型对称弯道，类型为大曲率比宽浅明流，底坡为平底坡。将流凌简化为球体颗粒，主要研究封冻前期结冰流凌的迁移，以及冰水耦合作用下弯道水力特性，探究冰水耦合作用下弯曲度不同弯道的流凌分布、水位、流速、湍动能(TKE)等指标的基本变化规律。

1 数值模型

1.1 水流控制方程

基于笛卡尔坐标的水流连续性方程和动量方程为

(1)

(2)

式中：ui为第i个方向(i=1，2，3)的速度分量；xi为第i个方向的空间坐标；p为压强；ρ为流体密度；Gi为第i个方向的重力加速度；τij为黏性应力；τbi为壁面剪应力，其在靠近实体边界处激活。可使用有限体积法结合流体体积法(VOF)来求解水流控制方程，以跟踪液体表面，并在液体表面应用适当的动力边界条件。还可利用广义最小残差求解器(GMRES)求解压力和速度。

1.2 湍流模型

RNGk-ε湍流模型可考虑旋流及反映平均应变率的主流[17]，适应于高剪切和分离区域，尤其适用于颗粒流情况下复杂水流的模拟，因此采用了RNGk-ε湍流模型模拟冰水两相流。

湍流模型由以下脉动能k和耗散率ε的输运方程组成：

(3)

(4)

式中：vt为流体涡黏度系数；μ为流体动力黏滞系数；模型参数cε1=1.42，cε2=1.68，c3=0.012,η0=4.38，cμ=0.085，αk=αε=1.39。模型中R的存在使湍流对平均应变速率更敏感。

1.3 粒子的动力学控制方程

(5)

拉格朗日粒子的扩散根据Monte Carlo方法进行计算，粒子之间不会相互影响。采用基于经验公式导出的阻力模型，该模型将阻力系数和球体与其周围流体的相对速度关联以计算阻力[18]。

(6)

粒子-流体耦合模型将离散质量粒子的动量与连续流体隐式耦合，两者的相互作用主要是动量交换，最终理论上颗粒的运动主要受重力、黏滞力、两相拖曳力以及根据压力梯度计算出的浮力等影响。描述每个相的方程式必须同时求解，两相动量耦合表示为阻力系数与相间相对速度的乘积。两相耦合基本方法：①根据未知的流体速度计算新的粒子速度；②将粒子速度代入流体动量方程中，并求解新的流体速度；③计算两相阻力及粒子速度[19]。

而颗粒与边界(壁边界)亦会产生碰撞，存在能量损失，所以模拟考虑恢复系数。该系数将颗粒与壁面碰撞前后的速度分为切向和法向速度，反射后与反射前粒子的法向速度分量之比即为恢复系数r，当r=1.0时，则在反射过程中不会发生粒子动能损失。

1.4 FAVOR技术

自由表面边界和流体界面使用流体体积法VOF处理：对任意网格点，若被流体占据则体积分数F=1，否则F=0。F是一个以0和1为边界的连续函数，由对流传输方程控制：

(7)

模拟采用FAVOR技术(fractional area /volume obstacle representation)来定义计算域，可在欧拉网格内定义实体边界，通过确定部分单元中开放面积和体积的分数模拟复杂形状。定义边界的过程独立于网格进行，消除和顺滑不平整区域，且可在特定区域做加密处理。

2 模型验证

2.1 粒子输移验证

通过对流凌拟颗粒化进行简化，引入具有离散相的冰颗粒，在此参照文献[20]，对引入颗粒的扩散性进行分析验证。试验内容为2 000个标记粒子初始条件下向x方向扩散，扩散系数为0.1 cm2/s，图1中展示了颗粒浓度分布，以总粒子数作无量纲化处理，以理论高斯曲线分布作为对比。可以看出，理论曲线和模拟曲线吻合良好，拉格朗日粒子模型可有效描述粒子扩散。

图1 不同时刻无量纲化点源粒子分布与理论高斯分布的比较

2.2 弯道水动力学模型验证

以Shukry弯道水流试验对CFD的水动力学模块进行验证[21]。Shukry矩形水槽弯道上游采取流量边界，给定初始水位0.3 m，同时给定恒定流量0.072 m3/s，沿程使用壁边界，下游使用压力出口，控制出口水位0.28 m。该数值模拟激活重力、湍流模型及密度变化模型，采用RNGk-ε湍流模型，对数值运算步长及压力迭代机制等进行参数控制，满足收敛性条件，对弯道速度、水位的实测值与模拟值进行对比验证，如图2所示。由图2可见，该模型平面流速与试验等值线图基本一致，最大流速在进口近凸岸处，在弯顶自凹岸向凸岸递增，在出口近凹岸侧。虽弯道速度最大值与试验值略有出入，但能够模拟出水动力轴线的迁移，较好地反映了实际水流水力特性。

图2 Shukry弯道水位和流速对比

模拟与实测水位变化范围均在0.20～0.33 cm之间，水位在弯道处呈现凹岸向凸岸递减的趋势，能够模拟水位凹岸高、凸岸低的水位特征。因此，采用的水动力学模型可用于模拟弯道三维水流运动特性。

3 模型建立及边界条件

参考周建银[22]被广为引用的系列水槽试验，建立单一弯道模型，其曲率半径与水槽模型一致，对入口、出口直道段及水槽高度进行适当延长加高，以满足拉格朗日粒子的充分输移。分别建立弯曲度不同的单弯模型，其中水槽弯曲段中心线半径长为 8.53 m，弯曲度分别为60°、90°、150°和180°，中心线曲率比为3.645，弯道底坡为平底坡。两个连接直道段长15 m，宽2.34 m，高1.2 m，初始水深0.8 m，模型尺寸如图3所示。

上游均采用流量进口，设置流量q=1.872 m3/s，进口水位0.8 m，水流弗劳德数Fr=0.357，平均流速vav=1 m/s，Re=470 422.7。下游采用压力出口，水位控制在0.65 m，流体经过区域采用壁边界，顶边界为大气压。采用结构化矩形网格，最小网格尺寸为0.12 m×0.12 m，计算时间200 s。参考野外实测数据，流凌前期冰花尺寸在5 cm左右，拉格朗日粒子模型设置为相同尺寸的mass solid particles，其直径为0.05 m，密度为917 kg/m3，与弯道边界接触后的恢复系数为0.5，阻力系数乘数设为1(意味计算域采用球体粒子充填)。水槽糙率设为0.015，静摩擦系数为0.5。粒子设为随水流运动，经过验算确定粒子源生成粒子速率为200个/秒。粒子和流体相互作用采用双向动量耦合，并采用控制变量法将无冰颗粒的清水流作为对照试验。

4 结果与分析

冰的密度小于水，主要分布于水体表层，对水流表层的水力特性影响较大，故以下主要从流凌分布、水面速度、横向环流、水位及湍动能变化几个方面探究流凌对弯道水流的影响。

4.1 弯道流凌分布

流凌在不同弯道输移特点如图4所示。由图4可见，弯曲度不同的各弯道，在达到稳定状态后，流凌在进口段及进入弯道初期(进口断面)的分布情况与直道分布相似。过弯道时，流凌前缘沿水流主轴线不断向前发展，随着粒子的集聚，逐渐向凹岸聚集，呈现凹岸多，凸岸少的特点，并沿凹岸输出弯道。出弯后流凌沿水流中心线左右摆动，随下游控制水位的影响，逐渐向两岸集聚。

图4 不同弯曲度弯道流凌输移及分布

另外，各弯道流凌沿凹岸逐渐增多扩散，流凌分布多呈现楔形分布，这与李淑祎等[23]在试验中的结论基本一致，因模拟无法对粒间相互作用力进行描述，该分布主要是流凌与槽间作用及弯道环流的影响所导致。各弯道速度较大流凌近凸岸，且随着弯曲度的增大，其范围逐渐缩小，高流速流凌数量沿弯道断面依次递减。流凌在凹岸的聚集，也解释了冰塞现象易集中停滞在弯道处，尤其在凹岸及回水区低流速区。

4.2 弯道流速及横向环流

4.2.1弯道流速

不同弯道冰水流和清水流表面流速等值线如图5所示。

图5 各弯道表面流速分布等值线

对于清水流，各弯道均在入口凸岸产生高流速区，出口凸岸产生低速区，这与Shukry弯道水槽试验规律基本一致。随着弯曲度的增大，主流越早偏向凸岸，弯道出口断面主流区向凹岸偏移程度随着弯曲度的增大不断加大[24]。

冰水流表面流速基本规律与清水流基本一致，主要不同在凹岸流态及主流区的改变。流凌在凹岸形成长条状低流速区，且沿水流该区域逐渐变宽。由上述冰凌运移规律可知，此处为流凌聚集处，聚集的流凌对凹岸流态产生了很大影响。随着弯曲度的加大，低流速区发展越广泛，冰花堆积越多。冰水流的主流亦因凹岸冰花的堵塞，向凸岸偏移程度变大，缩小主流过流面积。随上游流凌的不断堆积发展，此处极易形成冰塞体，并逐渐向上游递进，为河段险工部位。综上可见，由于流凌与水槽作用及弯道环流的存在，冰水流流速发展不充分，导致冰水流与清水流流速分布出现差异。

对各弯道冰水流及清水流流速进行定量分析，依据弯曲度的不同，对进口、弯顶、出口3个典型断面沿凹岸到凸岸水面流速分布进行分析。

如图6所示，60°弯道冰水流及清水流表面流速最大值均为v顶>v进>v出，出口断面冰水流速最小值小于清水流。90°弯道冰水流及清水流表面流速最大值均为v进>v顶>v出，进口断面两类流动相似，出口断面冰水流速最小值小于清水流，两类流动凹岸向凸岸流速变化剧烈。150°弯道冰水流及清水流表面流速最大值v进>v顶>v出，进口及出口断面两类流动速度相似，弯顶断面凹岸速度差异大，冰水流的速度更小。180°弯道进口及出口断面，两类流动表面流速分布基本一致，流速最大值v进>v出>v顶，凹岸向凸岸方向，弯顶断面冰水流速最小值小于清水流。综上可知，两类流动进口断面流速基本相等，弯顶及出口断面流速变化强烈。各弯道最大进口流速均大于出口流速，主要是凹岸流速发生变化。60°和90°弯道冰水流和清水流进口与弯顶断面水面流速基本一致，主要体现在出口断面的不同，150°和180°弯道冰水流与清水流进口与出口断面流速基本一致，主要体现在弯顶断面流速的不同。这是由于随弯曲度增大，凹岸低流速区离凸岸高流速区越远，低流速集中区延后。随着弯曲度增大，在弯顶断面，冰水流沿凹岸到水流中心流速差呈增大趋势，即冰水流在急弯河段弯顶部位，其低流速区范围更广泛。

图6 各弯道典型断面水面流速沿槽宽分布

如表1所示，除180°弯道，随着弯曲度的增大，冰水流与清水流弯顶断面凹岸流速最小值的差值呈增大趋势，而出口断面凹岸流速最小值的差值呈减少趋势，说明弯曲度对典型断面流速的影响逐渐由出口转向弯顶断面。

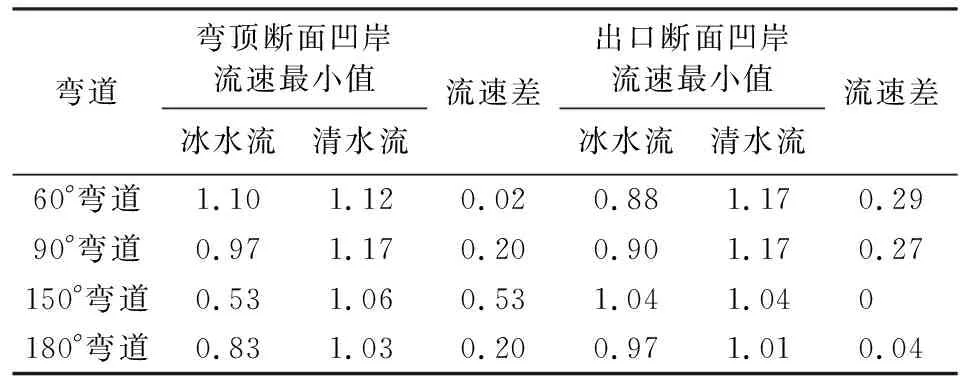
表1 不同弯道弯顶断面及出口断面凹岸流速变化 m/s

4.2.2 横向环流分布

为分析流凌条件下水流垂向分布特征，对流凌发展充分且流速变化大的180°弯道的典型断面进行分析，并与相同条件下清水流对比。不考虑纵向流速矢量，180°冰水流和清水流速度矢量图如图7所示。可以发现，在进口及出口断面，两类流动横向环流速度矢量基本相似，其中进口断面横向环流呈现自凹岸向凸岸变化的特征，而出口断面产生相似的对称环流，冰水流凹岸下有小环流。对弯顶断面分析可知，有流凌覆盖的条件下，凹岸形成愈加强烈的冰下环流，与靠近凸岸的大环流是对称关系，环流强度也小于后者。冰水流位于凸岸底部的大环流明显小于清水流，可能是由于积聚的流凌影响水流过流能力，在一定程度上影响凸岸的大环流的发展演化。

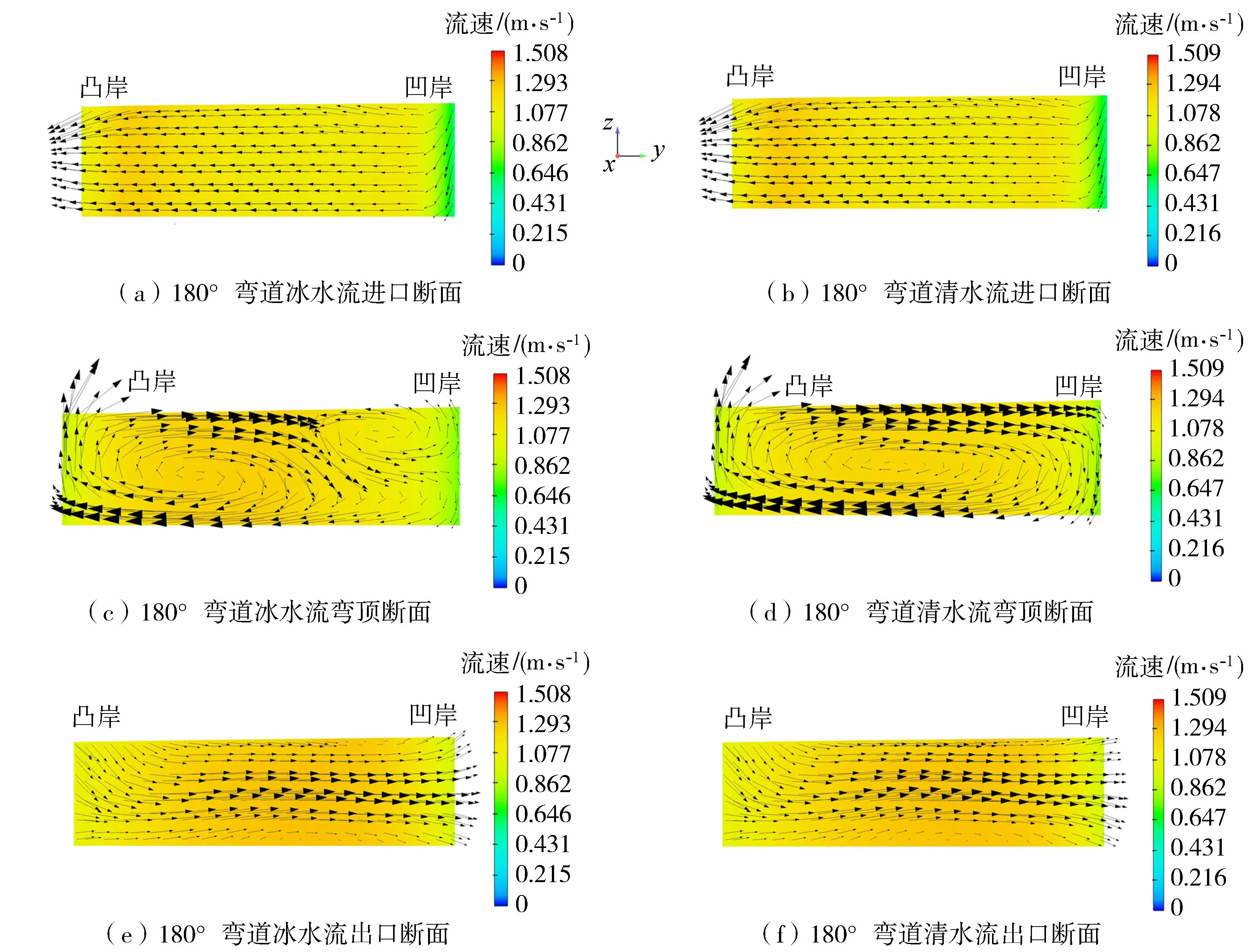
图7 不同弯道冰水流与清水流各断面横向环流分布

4.3 水位

为研究流凌对弯道水位的影响，对弯顶断面横向水位进行分析，由于离心力的存在而使自由水面的平衡状态遭到破坏，进入弯段即有从凸岸到凹岸倾斜的横比降Jr[25]，水深横向变化如图8和图9所示。各弯道凹岸到凸岸水位都有降低趋势，水面超高依次为0.03 m(60°弯道)、0.04 m(90°弯道)、0.06 m(150°弯道)和0.03 m(180°弯道)，说明弯曲度对宽浅明渠水深和水面超高有一定影响，但不明显。弯顶断面冰水流水位比清水流高，但随着弯曲度的增大两者差值变小。

图8 不同弯道弯顶断面冰水流与清水流水深变化对比

图9 各弯道弯顶断面的水深变化

4.4 弯道湍动能

从图10中看出弯曲度为60°、90°、150°、180°的弯道，清水流和冰水流湍动强烈部位主要从弯道入口处发展，集中于近岸两侧。凹岸高湍动能区冰水流比清水流宽，湍动较强，凸岸侧相似，凹岸向凸岸湍动能先减小后增大，呈U形分布。说明聚集的流凌冰在一定程度上增加了流体的湍动能，随弯曲度增大，湍动能呈增大趋势。