基于真空联合水平电渗法的水力冲挖淤泥脱水量计算方法
2021-09-14陈人瑗邱珍锋王俊杰武立清
杨 洋,陈人瑗,邱珍锋,王俊杰,武立清
(1.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122;2.华东勘测设计院(福建)有限公司,福建 福州 350003;3.重庆交通大学水工建筑物健康诊断技术重庆市高校工程研究中心,重庆 400074)
城市河道疏浚一般采用低浓度淤泥疏浚方式,如水力冲挖。水力冲挖产生的疏浚淤泥含水率高、体积大、固结难,直接堆场弃置会消耗大量的城市土地资源[1-2],增加社会矛盾和工程造价。疏浚淤泥黏粒小、沉淀慢、渗透性差、泥水自然分离时间长,传统脱水方法无法满足淤泥的脱水要求,开展淤泥中泥水快速分离方法的研究迫在眉睫。
许多学者对淤泥的脱水加固技术进行了研究。付冠杰等[3]提出了一种堆载吹填淤泥并同步真空预压加固技术,将吹填淤泥加固及软土地基加固两阶段施工整合到一个真空预压周期内完成以缩短造陆工期,但设置堆载所需要的材料成本和时间成本较高。房营光等[4]采用以砂垫层和竖向砂井为排水系统的真空预压法,进行了电渗法与真空预压法联合作用加固碱渣土以及软黏土的室内试验研究,证明了真空预压联合电渗法的有效性。王军等[5]通过室内试验发现,合理地设计电渗联合真空预压法,可以使两种作用产生相互促进的效果,电渗法可以提升远离排水板土体的加固效果,真空预压法可以降低电渗阴极的含水率。Wang等[6]采用电渗联合真空预压法处理淤泥,当真空预压处理效果下降时再开启电渗装置。陶燕丽[7]发现在电渗过程中,黏土的排水速率与电流存在线性关系,以此为基础,可以通过经验公式计算黏土的排水量。刘凤松等[8]开展了大面积真空-电渗降水-低能量强夯联合地基加固方法研究。俞家锐等[9]对温州苍南县江南围垦区进行真空预压-电渗加固现场试验,结果表明真空预压-电渗联合加固法取得了良好的效果,不仅地基承载力超过了预期,且相对于真空预压法在缩短工期上优势明显。储旭等[10]结合福建省厦门市丙洲浅滩陆域形成工程实践,将抽真空、电渗、强夯三者的优势相结合,不但能改变传统地基处理方式的应用局限性,而且能有效降低工程造价,缩短工期,提高处理后土体的强度,并具有无二次污染的特点。从以上研究可看出电渗固结脱水技术能有效提高软土的固结度、缩短固结时间,解决低渗透性地基排水固结问题[11-13]。但是针对“超高含水率”的城市河道水力冲挖淤泥,真空联合电渗法及其脱水处理效果评价方法的研究还较少[14]。已有的真空联合电渗技术[15-18]存在以下问题:①淤泥处理堆场中淤泥往往深度较浅,真空预压法的经济性不能体现;②电渗法的电极往往是竖直布置,处理后的电极之间产生自上而下的贯穿裂缝,这种纵向裂缝直接阻断了阴阳极之间的电流,严重影响电渗效果。
佘鹏等[19]通过试验对比了水平电渗和竖向电渗的固结效率,结果表明水平向电场的脱水效果明显优于竖直向电场的脱水效果,水平向电场降低了淤泥固结后开裂对电渗效率产生的影响,且电极区排气问题也更易于处理。周详等[20-21]将电极设计为水平布置,形成真空联合水平电渗脱水法,在此基础上,本文开展水平电渗联合真空预压的冲挖淤泥脱水试验研究,提出水力冲挖淤泥脱水量计算方法。计算思路为将电渗作用与真空作用分开考虑,分别计算两种作用排出的脱水量,最后进行叠加。将叠加之后排水量理论计算值与实测值进行对比,对计算公式进行修正,综合考虑得出总脱水量。
1 真空作用下脱水量计算
1.1 试验方法
为测定真空作用下淤泥的脱水量,进行了真空作用下脱水量测定试验。在模型试验过程中,仅使用真空排水结构对骆家沟水力冲挖淤泥进行处理,试验布置如图1所示。试验槽长1.0 m,宽0.6 m,试验槽底部布置真空滤管排水结构。将裁好的不锈钢钢筋按一定间距固定在薄木板上制成阳极;在直径为5 cm的PVC管上钻制排水孔,管外包裹两层土工布以过滤淤泥,通过弯头拼接阴极。阴极布置于淤泥底部,阳极布置于淤泥表面。淤泥自重作用可以有效抑制阴阳极之间的裂缝开展;阳极位置随淤泥沉降而降低,阴、阳极距离不断减小,电势梯度不断增大,有利于提升电渗脱水效果。淤泥表面至试验槽底部高0.4 m,淤泥密度1.022 g/cm3,初始含水率为470.0%。采用底部6支真空滤管持续工作,不开启电渗电源的试验方案。试验过程中监测水气分离罐中的累计脱水量。上部淤泥最靠近阳极,此处电场强度最大,再加上重力场作用,加速上部水分向下部运移。因此呈现上部含水率变化较剧烈,底部含水率变化较缓和,中部含水率变化范围相对较小。为减小试验结果的误差,每24 h取试验槽中部淤泥测量含水率。
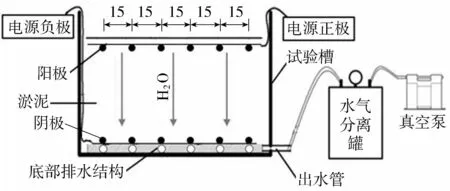
图1 试验布置示意图(单位:cm)
1.2 试验结果分析
真空作用下淤泥含水率随时间的变化如图2所示。从图2可以看出,随处理时间的增加,淤泥含水率不断降低且降低速率逐渐减缓。前24 h含水率下降速率较大的原因可能是淤泥初始含水率大,导致大量液态水通过滤管排出;24 h后含水率近似线性减小,且含水率降低速率明显低于前24 h,其原因是真空滤管附近淤泥的含水率下降较快,远离滤管的水分又未及时运移到滤管附近,因此排水速度减慢。
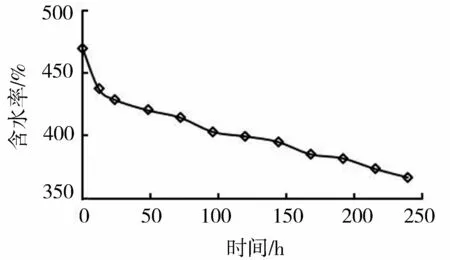
图2 含水率随时间变化
在试验过程中,观察到24 h后,水气分离罐中的水量增加十分缓慢,仅有少量的水滴排入罐内。试验结束后,水气分离罐中收集到的液态水质量仅为17.125 kg。含水率测试数据表明,240 h时淤泥试样的含水率为366.7%,较初始含水率降低103.3%。假设淤泥含水率均匀分布,已知含水率变化,淤泥脱水质量可由下式计算:
(1)
式中:mv为真空作用下脱水质量,kg;w0为淤泥初始含水率,%;w为处理后淤泥含水率,%;m0为淤泥初始质量,kg。
通过式(1)计算得到真空作用下淤泥脱水质量为44.471 kg,明显大于水气分离罐中收集到的液态水质量17.125 kg,可算出气态水的质量为27.346 kg,液态水和气态水的质量比约为3∶5。这说明淤泥中排出的水仅有一部分以液态形式贮存于水气分离罐中,另一部分以水蒸气的形式排出。
为了进一步探究淤泥脱水规律,分析脱水过程中脱水速率的变化情况,对比理论脱水速率与水气分离罐实际收集到的液态水脱水速率。理论脱水速率可以表示为当前时段单位时间脱水量,即:
(2)
式中:q为当前时段总脱水速率,kg/h;Δt为时长,取为Δt=24 h。
将式(1)代入式(2)得:
(3)
脱水速率与时间的关系如图3所示。由图3可知,处理过程的前48 h,理论脱水速率迅速减小,与实际收集到的液态水脱水速率变化趋势基本一致。这是由于处理前期,滤管排水结构附近淤泥含水率极高,绝大部分水以液态形式在真空与重力作用下排出,被收集在水气分离罐中。在48~240 h时段内,理论脱水速率平均值在0.123 kg/h附近波动,而将水气收集罐中的液态水质量视为实际脱水量换算得平均脱水速率仅为0.008 kg/h。这是由于此阶段水主要以气态排出,并未被水气分离罐所收集到。将真空作用下淤泥的脱水过程分为两个阶段:①快速排水阶段。淤泥在处理开始的一小段时间内脱水速率大,且以液态水为主,但速率衰减也很快。此阶段淤泥含水率极高,液态水在重力和真空共同作用下快速排出,且重力作用对脱水速率影响很大。②稳定促排阶段。在第一阶段后的大部分时间内,水分主要以气态的形式排出外界,且脱水速率在本阶段平均值附近波动。此阶段重力脱水作用可以忽略,真空作用为主要促进作用。

图3 真空脱水速率随时间变化
1.3 真空作用下脱水量计算公式
根据以上试验结果与分析,作出以下假设:①真空作用下水均以气态排出(快速排水阶段重力作用排出的液态水归入到电渗作用中考虑,具体计算方法在第2节中介绍);②淤泥体内部含水率均匀减小。由此可以得出真空作用下脱水量计算公式为
(4)

2 水平电渗作用下脱水量计算方法
2.1 基本假设
已有许多学者发现,对于不同类型的土体,电渗脱水速率与电流均呈线性关系,且土体含水率与土体电导率往往存在线性关系、指数关系或二次函数关系等,可以通过一些经验公式来计算土体的电导率[22]。假设水平电渗脱水量符合以下规律:①脱水速率与电流存在线性关系,即:q=CI,I为电流,C为与淤泥自身性质相关的常数;②电导率与含水率呈线性关系[23](式(5))、指数关系[5](式(6))或二次函数关系[24](式(7))等较为简单的关系;③电渗过程中,土体各处含水率均匀减小,即均匀分布;④电渗作用下水分全部以液态排出并贮存于水气分离罐中,真空促排作用排出的水分全部以气态逸出外界。
σ=Aw+B
(5)
(6)
σ=(Aw+B)2
(7)
式中:σ为淤泥电导率,S/m;A、B、D为与淤泥的物理性质相关的常数。
2.2 公式推导
根据电渗过程中假设③和④得到土体含水率随脱水量的变化为
(8)
式中:me为电渗脱水量,kg。
假设待处理淤泥长、宽、高分别为l、a、b,电导率可由下式计算得到:
(9)
式中:U为电源电势,V。
根据假设①和式(9)得:
(10)
以电导率为等量关系,分别将式(10)与式(5)(6)(7)联立,将初值条件me(0)=0代入微分方程的通解,得到电导率与含水率的不同关系式,进而得到如下3种不同的电渗脱水量me与时间t的关系式:
(11)
(12)
(13)

2.3 计算方法验证
为验证上述3种脱水量计算方法的准确性,进行了水平电渗作用下脱水量测定试验。采用图1试验模型对骆家沟水力冲挖淤泥进行水平电渗脱水处理。为确定骆家沟水力冲挖淤泥电导率相关参数,模型试验采用持续电渗的通电方式,电源电压为30 V,淤泥初始含水率为441%。
电渗脱水速率与电流的关系如图4所示,可见脱水速率和电流的关系符合假设①,可以用线性函数来拟合,比例常数C=0.188 6。

图4 电渗脱水速率与电流关系
根据式(8)和式(9),计算处理过程中含水率和电导率值,以含水率为横坐标,电导率为纵坐标绘制散点图(图5)。采用式(5)拟合数据点时,得到骆家沟水力冲挖淤泥的材料参数A=0.471 9,B=-1.227 5;采用式(6)拟合时,得到A=0.062 7,D=1.353 4,B=-0.411 1;采用式(7)拟合时,得到A=0.520 2,B=-1.172 0。根据式(11)(12)(13),计算得到了3种拟合方式下淤泥的电渗脱水量,见图6。
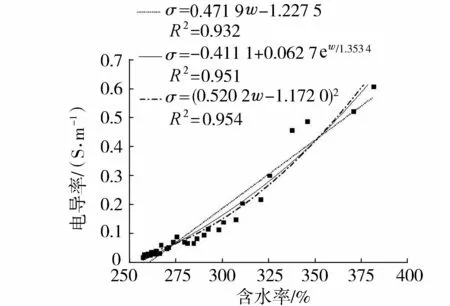
图5 电导率与含水率关系

图6 水平电渗脱水量计算结果
残差平方和可以用来评价模型计算值与实测值的拟合程度。式(11)(12)(13)的残差平方和分别为190.96 kg2、185.22 kg2和171.25 kg2,其中式(13)的残差平方和最小,拟合效果最优。但总体来讲,采用3种拟合方式计算出的电渗脱水量与模型试验实测值趋势和形态吻合均较好。这说明基于电导率的水平电渗脱水量计算方法能够较好地拟合水力冲挖淤泥电渗脱水过程。
3 总脱水量计算方法
假设基于真空联合水平电渗法的脱水量计算方法符合以下规律:①淤泥的总脱水量是电渗作用与真空促排作用分别作用的叠加;②脱水速率与电流存在线性关系;③淤泥的电导率与含水率具有指数关系;④处理过程中,土体各处含水率均匀减小,即均匀分布;⑤电渗作用下水分全部以液态排出并贮存于水气分离罐中,真空作用排出的水分全部以气态逸出外界。总脱水量计算公式为
(14)
式中:m为基于真空联合水平电渗法的总脱水量,kg。
为了验证本文计算方法的适用性和上文所测参数的可靠性,设置了小尺寸模型试验,应用上文所得参数,预测模型试验的脱水量。试验在18 V电源电压下进行,试样仍采用骆家沟水力冲挖淤泥,试验按照图1布置,水力冲挖淤泥初始含水率为448%,淤泥密度为1.022 g/cm3。
根据第2.3节中获得的水平电渗参数,分别计算3种拟合方式下水平电渗脱水量与实测脱水量(13.18 kg)的相对误差和残差平方和如表1所示。绘制水平电渗脱水量随时间变化的关系曲线(图7),并与实际收集到的液态水质量进行对比。
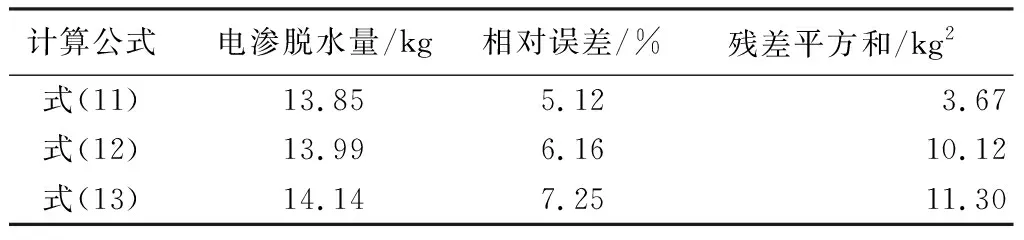
表1 水平电渗脱水量误差统计

图7 水平电渗脱水量计算结果与实测值对比
由图7可见,采用3种拟合方式计算出的水平电渗脱水量与模型试验实测值趋势和形态吻合较好。这说明基于电导率的水平电渗脱水量计算方法能够较好地拟合水力冲挖淤泥电渗脱水过程。结合表1数据可得,3种拟合方法中,式(11)的残差平方和最小,电渗脱水量相对误差最小,拟合效果最优。同时考虑到式(11)计算公式简单,电渗脱水量计算仅需要确定A、B两个参数,因此,采用线性关系拟合电导率与含水率关系对于计算骆家沟水力冲挖淤泥电渗脱水量具有一定的优越性。

根据式(8)计算试验结束时淤泥的理论含水率为93.30%。为了检验计算结果的可靠性,再一次对试验结束时淤泥的含水率进行测试,含水率取样点位置如图8所示,测试结果如表2所示。

图8 含水率测量点位置(单位:mm)

表2 含水率测试结果
由表2可得,淤泥上部较干燥,含水率平均值为86.15%,下部较湿润,含水率平均值为137.67%,整体含水率平均值为94.23%。由于脱水处理时淤泥内部的水分流动方向是由上部的阳极流向下部的阴极,因此脱水处理后的淤泥呈现上干下湿的现象。理论含水率是假设淤泥体含水率分布均匀时通过式(8)计算出的,对比含水率测试结果,其值93.30%处于干燥位置含水率值和湿润位置含水率值之间,且与试验测得的整体含水率94.23%接近。这进一步验证了本文提出的基于电导率的脱水量计算方法的适用性。
4 结 论
a.真空作用下,淤泥的脱水过程可分为主要排出液态水的快速脱水阶段和主要排出气态水的稳定促排阶段,液态水和气态水的质量比约为3∶5。
b.对于骆家沟水力冲挖淤泥,电渗脱水速率与电流呈线性关系,土体的电导率与含水率呈线性函数、指数函数或二次函数关系,其中基于线性函数关系拟合得到的电渗脱水量与模型试验实测值之间的残差平方和最小,相对误差最小。
c.根据本文提出的计算方法计算得到的总脱水量所对应的淤泥理论含水率与模型试验实测值仅相差1%,表明将真空作用和水平电渗作用下脱水量分别计算后再叠加用于估算水力冲挖淤泥脱水量是基本合理的。
