基于置信规则库的油浸式变压器故障诊断

2021-09-14易照云

北京工业大学学报 2021年9期

胡蓉，易照云，钱斌

(昆明理工大学信息工程与自动化学院，昆明 650500)

电力变压器可分为干式变压器和油浸式变压器. 油浸式变压器充满了既能作为传热流体、又能作为电绝缘材料的矿物绝缘油，又称变压器油. 当变压器老化，变压器的电应力和热应力随之增大，变压器油会腐烂，并释放几种气体溶解在油中. 这些气体包括氢气(H2)、甲烷(CH4)、乙烯(C2H4)、乙炔(C2H2)和乙烷(C2H6)五种主要气体，它们通常被用于变压器初期故障诊断[1]. 变压器是保证电力系统连续正常运行的核心，因此，为保证变压器正常运行，变压器故障的初期诊断变得十分重要.

近年来,油浸式变压器在线状态的初期故障诊断技术得到了快速的发展. 传统的油浸式变压器故障诊断技术包括Duval三角形法[2]、关键气体法[3]和比率法[4]等，这些传统方法简单易行，但缺乏对变压器故障数据和故障类型间复杂非线性关系的有效刻画和处理，诊断结果的准确性和可靠性有待提高. 因此，研究者也采用人工智能(artificial intelligence, AI)模型诊断油浸式变压器的早期故障. 这些模型包括人工神经网络(artificial neural network，ANN)[5]、支持向量机(support vector machines，SVM)[6]和粗糙集理论[7]等. 然而，现有的AI诊断模型也存在一些局限，例如：ANN模型容易过度拟合且可解释性差，SVM模型对参数和核函数敏感，粗糙集模型在很大程度上忽略了规则的信息特征[8-9].

针对AI模型的不足，近年研究者也提出了一些改进措施. Yang等[10]采用基于交叉和变异概率的自适应遗传算法对概率神经网络模型的参数进行优化，提高了模型的预测精度. Wang等[8]将关联规则引入粗糙集模型，增强了模型对海量数据的挖掘能力. Ma等[1]利用粒子群优化(particle swarm optimization，PSO)算法对向量机分类模型的参数进行优化，提高了模型的鲁棒性和对变压器故障的诊断精度. 由上述研究可知，对于神经网络和SVM这类非线性非凸模型，可利用智能优化算法确定模型参数，从而提升模型的性能.

置信规则库(belief rule base, BRB)是一种基于规则的专家系统，可对具有非线性、模糊关系的数据进行有效建模[11]. BRB系统通过在一系列传统的IF-THEN规则中加入置信度、前提属性和规则权重建立模型. 因此，BRB具有很强的刻画非线性因果关系的能力且具有非常直观的可解释性. 目前，它已经成功应用于医疗系统诊断[12]、水松纸透气度检测[13]、产品寿命评估[14]等领域.

虽然BRB系统在建模上已表现出较强的能力，但由于BRB模型是由多个复合函数组成的非线性非凸模型[13]，这导致一方面模型规模随规则数量、前提属性和规则权重等参数增加而明显增大，另一方面模型参数的优化难度较大. 显然，建立有效BRB模型的关键在于如何在控制模型规模前提下确定模型参数. 已有研究侧重模型结构的简化，而对简化后的模型基本直接采用MATLAB中的非线性优化求解器，即FMINCON函数来优化确定BRB模型参数[9，15]. FMINCON函数采用传统数学规划方法中的梯度下降法对优化问题进行求解. 然而，梯度下降法存在对初始值敏感、收敛慢、易陷入局部最优的不足. 这在一定程度上限制了BRB的应用效果.

人群搜索算法(seeker optimization algorithm, SOA)由Dai等[16]于2006年首次提出，是求解非线性连续优化问题的有效算法之一. SOA是模拟人类搜索活动智能行为的一种群搜索算法. 该算法可并行执行本地搜索和全局搜索，具有较强的搜索能力，此外，SOA也易于理解和实现. 这些特点使其被成功用于求解多种复杂连续优化问题[17-18].

鉴于BRB的建模优势和SOA的优化能力，本文提出了基于BRB的油浸式变压器故障诊断模型. 首先，利用变压器中不同溶解气体的故障数据和故障类型建立置信规则联系，并结合证据推理(evidential reasoning, ER)法将输入转化为输出的故障类型判定值，进而初步确定BRB模型的结构. 其次，借鉴文献[19]中的维度约减思想，通过约减故障气体类型和减少训练模型参数实现BRB模型结构的合理简化. 然后，设计一种具有自适应更新策略(adaptive update strategy, AUS)的SOA(AUS-SOA)对简化后的BRB模型参数进行优化，进而建立故障诊断模型AUS-SOA-BRB. 最后，采用文献[20-22]中的48组油浸式变压器溶解气体故障数据进行测试，验证了AUS-SOA-BRB模型的有效性.

1 基于BRB的诊断模型和诊断过程

1.1 基于BRB的诊断模型结构

BRB系统本质上是一种专家系统.假设一个BRB共由L条置信规则组成，则BRB模型的第k条规则表示的向量形式为

RK：IfxisAkThenD
With belief degreeβk

(1)

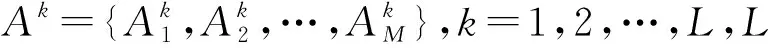
1.2 基于BRB的变压器诊断模型的ER方法

ER算法是利用证据推理对BRB中的置信规则进行组合，通过输入信息x得到故障诊断的估计值j，从而得到BRB系统的最终输出S(x).ER算法的推理步骤主要包含以下3个部分.

1) 不同输入信息的转化方法.

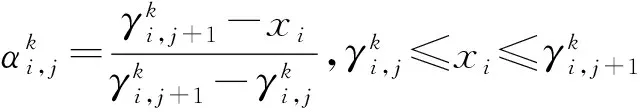
(2)

(3)

(4)

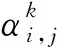
2) 置信规则库激活权重的计算.

输入信息x，对应的第k条规则的ωk的计算方法为

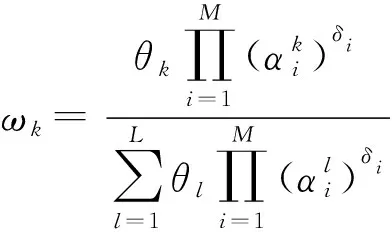
(5)

式中：ωk为激活权重，ωk∈[0,1];θk为第k条规则的规则权重，初始θk由专家给定；δi为第i个前提属性权重.

3) ER解析算法的推理计算.

ER解析算法的推理计算公式为

(6)

(7)

式中：βj,k为第k条规则下对应第j个评价结果参考值的置信度；j为相对评价结果Dj的置信度.

通过ER解析算法对BRB中所有规则进行组合，得到BRB的最终输出为

S(x)={(Dj,j),j=1,2,…,N}

(8)

1.3 诊断过程

首先，通过式(1)建立油浸式变压器故障气体输入数据x与输出故障评判数值j之间的映射关系.其次，由专家给定输入参考值进而通过式(2)～(4)将不同规则下输入的故障数据转化为对应输入参考值的置信度，为计算BRB激活权重做准备.然后，在已知规则权重θk和输入置信度下，由式(5)计算第k条规则的激活权重.最后，通过式(6)～(8)推理计算出对应故障等级参考值的评价结果Dj和置信度j，从而诊断出油浸式变压器故障类型.

在ER中，规则权重θk、置信度βj,k和前提属性权重δi对输出S(x)有显著影响.因此，本文提出了AUS-SOA算法对BRB模型参数进行优化，以使优化后的模型AUS-SOA-BRB可对变压器故障进行有效诊断.

2 故障诊断训练模型和算法

2.1 基于BRB的变压器故障诊断训练模型

变压器故障诊断模型的估计输出故障类型和实际输出的故障类型的差异关系，由实际故障类型置信度βi(m)与估计输出置信度i(m)的误差决定.对于给定的一组实际输入输出的检测值(xi(m),βi(m))，通过式(2)～(7)可求出估计输出i(m)，从而由多组数据可得平均误差ξ(V)为

(9)

式中：V=[θk,βj,k,δh]T为由BRB系统参数(即需优化的决策变量)构成的列向量；T为训练数据的数量；i为第i条规则；abs(·)为对输入的元素取绝对值.

为了减小实际系统得到的故障类型判定结果与SOA-BRB诊断模型得到的故障类型诊断结果的误差，变压器故障诊断训练模型对应优化问题的目标函数为

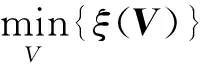
(10)

式中，模型的约束条件为

0≤θk≤1,k=1,2,…,L

(11)

0≤βj,k≤1,j=1,2,…,N,k=1,2,…,L

(12)

(13)

0≤δh≤1,h=1,2,…,M

(14)

2.2 故障气体类型的约减和训练模型的简化

BRB模型结构具有较强非线性且模型参数的数量随着问题规模的增加而明显变多，模型的复杂度增大.前提属性权重δh反映了5种故障气体对故障诊断的重要程度，可影响故障诊断的准确度，合理选择δh能够在降低模型复杂度的同时提高故障诊断的精确度.因此，如何合理降低模型复杂度是BRB建模的关键环节之一.对于本文的优化问题，约减故障气体类型和简化训练模型可有效控制对应优化问题的复杂程度[19].该约减和简化过程具体如下.

首先，根据1.1节和1.2节的置信度j估计方法(即式(1)～式(6))，用5种故障气体数据建立2.1节的BRB故障诊断训练模型(即式(10)～式(14))，并采用SOA对该训练模型参数进行适当优化，得到模型参数θk、βj,k、δh；然后，选择前提属性权重δh较优值中最大的3个值对应的3种故障气体数据作为变压器故障诊断数据，进而将已选中的3种故障气体前提属性权重δh设置为1，将决策变量或优化变量V=[θk,βj,k,δh]T简化为V=[θk,βj,k]T.通过SOA优化选择出的3种前提属性权重δh可以看作是必然前提属性，即令其权重为1，这样既能降低模型的复杂度，又能在一定程度上提高故障诊断的效率和精确度.BRB的激活权重由式(5)简化为

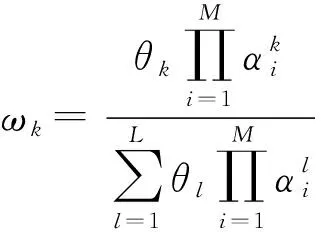
(15)

基于BRB的故障诊断系统参数优化过程见图1.

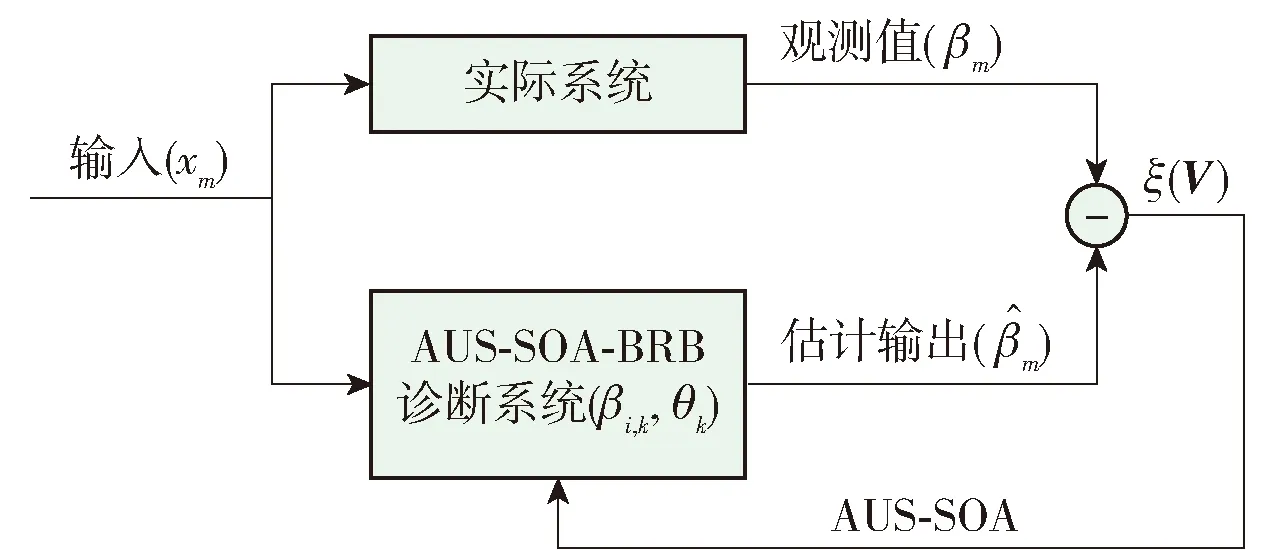
图1 基于BRB的故障诊断系统参数优化过程Fig.1 Parameter optimization process of fault diagnosis system based on BRB

2.3 AUS-SOA

2.3.1 SOA

SOA采用人类搜索行为的方法和不确定性的模糊逻辑对上述搜索规则进行建模，并确定步长.因此，实现SOA要完成如下3个阶段.

1) 第一阶段：搜索方向的确定.

SOA通过模拟人的社会学习和认知学习,获取社会经验和认知经验,并通过这些经验模拟人的3种行为(利己行为、利他行为和预动行为)来确定个体的搜索方向.第i个搜寻个体的搜索方向由以下3个方向确定.

利己方向

di,ego：di,ego(t)=pi,best-xi(t)

(16)

利他方向

di,alt：di,alt(t)=gi,best-xi(t)

(17)

预动方向

di,pro：di,pro(t)=xi(t1)-xi(t2)

(18)

式中：gi,best为第i个搜寻个体所在当代的种群历史最优解位置；pi,best为第i个搜寻个体搜索到当前为止的历史最优解位置；xi(t)为第i个搜寻个体当前位置，t为当前进化代数，t1,t2∈{t,t-1,t-2};xi(t1)和xi(t2)分别为{xi(t-2),xi(t-1),xi(t)}中最优的位置.

第i个搜寻个体的搜索方向采用式(16)～(18)所示的3个方向随机加权几何平均确定，公式为

di(t)=sign(ωdi,pro+φ1di,ego+φ2di,alt)

(19)

式中：sign(·)为输入矢量每一维的符号函数；ω为随进化代数从0.9线性递减到0.1的惯性权重；φ1和φ2为在[0,1]内服从正态分布的形式被随机选取的实数.

2) 第二阶段：搜索步长的确定.

第i个搜寻个体搜索步长的确定是建立在目标函数和步长之间不确定性的模糊推理行为.搜索步长的模糊变量采用高斯隶属函数，可表示为

uA(x)=exp[-(x-u)2/(2δ2)]

(20)

式中：uA为高斯隶属函数；x为输入变量；u、δ为高斯参数.当uA(x)超出[u-3δ,u+3δ]，uA(u+3δ)<0.011 1时，可取umin=0.011 1，umax=1.

种群位置的高斯隶属度可表示为

(21)

uij=rand(ui,1),j=1,2,…,D

(22)

式中：ui为目标函数值i的隶属度；uij为j维空间目标函数i的隶属度，uij∈[ui,1]；Ii为种群函数值按降序排列后xi(t)的序列编号；m为种群规模；D为搜索空间维数.

第i个搜寻个体搜索步长为

(23)

δij=ω·abs(xmin-xmax)

(24)

ω=(Tmax-t)/Tmax

(25)

式中：αij为j维搜索空间的步长；δij为高斯隶属函数参数，是δij的数值形式；xmin和xmax分别为同一子群中具有最小和最大函数值的位置；t和Tmax分别为当前迭代次数和最大迭代次数.

3)第三阶段：搜寻个体的位置更新.

当第i个搜寻个体搜索方向和搜索步长确定以后，其位置更新公式为

Δxij(x+1)=αij(t)dij(t)

(26)

xij(t+1)=xij(t)+Δxij(t+1)

(27)

式中：xij(t+1)为在t+1代时，第i个搜寻个体在第j维搜索方向的位置；dij(t)为第i个搜寻个体在第j维的搜索方向.

2.3.2 AUS

由SOA的第一阶段式(16)～(19)可知，传统的个体搜索方向由pi,best、gi,best以及最近3代范围内的历史最优解位置共同确定，这样加快了算法收敛于局部最优解的速度，同时增强了算法开采局部最优解的能力.然而，传统SOA在快速找到局部最优解的同时，使得解的搜索范围易陷入局部最优，进而削弱了SOA对整个解空间的开采能力.

为了提高SOA对整个解空间的开采能力，本文提出AUS-SOA，具体描述分为2种更新方法.

1) 第一种更新方法.

当

(28)

时，执行

(29)

2) 第二种更新方法.

当

(30)

时，执行

(31)

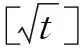
式(28)(30)是利用ξ(V)下降速率与迭代次数的关系设置迭代过程中的选择机制.前期迭代过程中ξ(V)下降速率较快，式(28)选择机制保证了对SOA局部搜索能力强的优势的保留.随着迭代次数的增加，ξ(V)下降速率较慢，并逐步收敛，式(30)选择机制生效，并将更新过程由式(29)转向式(31)，跳出SOA的快速收敛趋势，扩大优质解的搜索范围.因此，自适应的选择机制是自适应更新策略的核心.本文提出的自适应更新策略是在很大程度上保留原算法优势的同时，采用自适应的选择机制增强对整个解空间的开采能力.

2.4 约束处理方法

约束处理是一个重要的研究领域，其应用广泛，并取得不错的效果，如产品配置、任务规划与调度以及空间推理等[23].鉴于此，本文对BRB的故障诊断模型的约束条件进行适当的处理以提高BRB结构对参数调整的高效性.

由2.1节可知，变压器故障诊断模型的约束条件的处理方法转化为

(32)

(33)

(34)

2.5 AUS-SOA-BRB的构建

根据以上对油浸式变压器故障诊断优化训练模型和AUS-SOA优化算法的描述，基于置信规则库的油浸式变压器故障诊断模型的具体实现步骤(结合图2)如下.

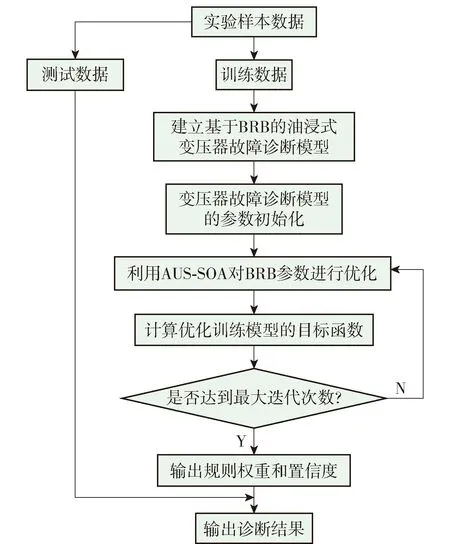
图2 基于BRB的油浸式变压器故障诊断流程图Fig.2 Fault diagnosis flowchart of oil-immersed transformer based on BRB

步骤1将故障气体数据转化为实验样本数据，并分组为训练数据和测试数据.

步骤2建立基于BRB的油浸式变压器故障诊断模型.

步骤3初始化油浸式变压器故障诊断模型的参数.

步骤3.1θk以在[0,1]内服从正态分布的形式被随机选取.

步骤3.2输入训练样本数据，通过式(2)～(4)将实验样本数据转化为对应的置信度βj,k.

步骤4利用AUS-SOA对BRB的初始化参数进行优化步骤：

步骤4.1利用式(28)～(31)确定每个搜寻个体的搜索方向.

步骤4.2利用式(21)～(26)确定搜寻个体的搜索步长.

步骤4.3利用式(27)，结合式(32)～(34)对每个搜寻个体的位置进行更新.

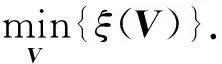
步骤6判断AUS-SOA的迭代次数是否达到最大迭代次数，若满足终止条件，则输出规则权重θk和置信度βj,k，反之返回步骤4.

步骤7输入测试样本数据，并输出诊断结果S(x).

3 变压器故障诊断实例分析及比较

3.1 实例描述

本文采集了文献[20-22]给出的48组小规模变压器故障气体数据样本约减后作为实验数据，以验证本文所提方法的有效性.为提高实验结果的准确性，本文采用循环实验的方法，扩大训练数据和测试数据的规模，具体实施步骤如下.

步骤1利用前15组数据作为测试集，剩下的作为训练集.

步骤2利用第16～30组数据作为测试集，剩下的作为训练集.

步骤3利用第31～45组数据作为测试集，剩下的作为训练集.

循环实验将实验数据扩大为144组，其中测试集扩大为45组，训练集为99组.这些故障数据包括了变压器5种工作状态，即正常状态(normal，N)、低能放电(low-energy discharge，LE-D)、中温和低温过热(medium and low temperature overheating，ML-T)、电弧放电(arc discharge，AD)和高温过热(high temperature overheating，HT).正常状态、低能放电、中低温过热、电弧放电和高能过热5种工作状态分别表示为{10000}、{01000}、{00100}、{00010}和{00001}.

为构建BRB故障诊断模型，设置5种故障气体的体积分数的参考值.5种故障气体的体积分数参考值的类型及量化值见表1.

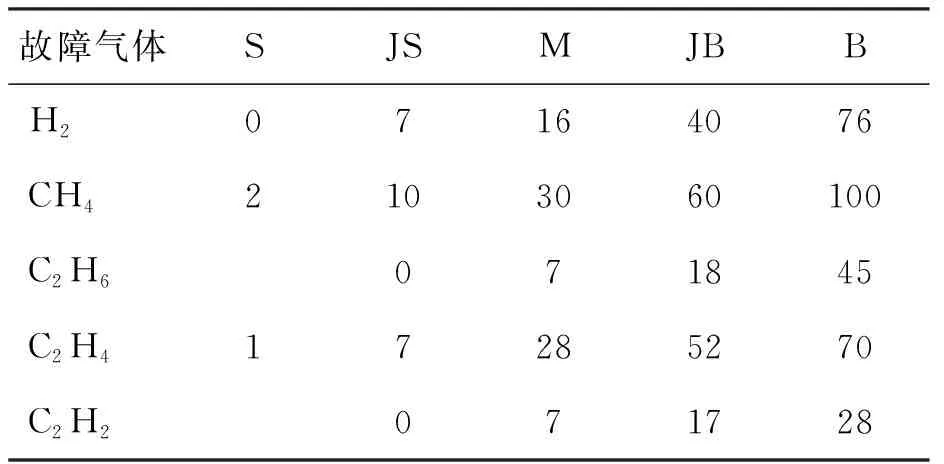
表1 5种故障气体体积分数的的参考值

参考值的类型共分为小(S)、较小(JS)、中等(M)、较大(JB)和大(B)五种，即D=(D1,D2，…，D5)=(S,JS,M,JB,B).

对H2、CH4、C2H4分别选取5个参考值，即小(S)、较小(JS)、中等(M)、较大(JB)和大(B).对C2H6和C2H2分别选取4个参考值，即较小(JS)、中等(M)、较大(JB)和大(B).

由表1得到置信规则数为5×5×4×5×4=2 000条.

3.2 故障气体类型的约减和训练模型的简化

利用3.1节本文采集的45组变压器故障气体数据作为训练数据.初始化θk、βj,k和δh，由专家以在[0,1]服从正态分布的形式随机选取并确定θk、βj,k和δh的值，然后通过SOA对BRB变压器故障诊断模型进行训练.SOA的初始参数设置为：ωmax=0.900,ωmin=0.100;umax=0.950,umin=0.011，种群数为60，进化代数(迭代次数)为500.为确保前提属性权重训练结果的有效性，取10次训练结果的平均值作为最终的训练结果，训练后的前提属性权重见表2.

表2 前提属性权重训练结果

根据表2所示的5种故障气体的权重训练结果，选取权重值最大的3种故障气体数据作为实验数据.故障气体数据类型约减后，将5种前提属性转化为3种前提属性，即{H2，CH4，C2H4}，同时设置其前提属性权重δh为1，此外置信规则库的规则数变为125.

3.3 基于BRB的故障诊断模型训练结果

本文利用3.1节所描述的循环实验方法进行变压器故障诊断实验.首先，由专家以在[0,1]服从正态分布的形式随机选取并确定初始θk和βj,k的值，然后代入训练数据，并利用SOA、AUS-SOA分别对BRB模型进行优化训练，其中SOA的参数设置及迭代次数与3.2节的相同.由于篇幅有限，本文只列出了第1次循环实验中，由AUS-SOA算法训练后的前40条置信规则所对应的规则权重和置信度作为参考(见表3)，并给出了训练集的故障诊断结果(见表4).由表4可知，基于BRB的变压器故障诊断模型在AUS-SOA的优化下，对训练集的故障诊断正确率约91%.

表3 训练后BRB中的规则权重和置信度

此外，本文给出SOA在自适应改进策略下的变压器故障诊断的平均误差适应度曲线，如图3所示，进一步验证了带AUS的SOA比传统的SOA更加有效.图3为算法迭代20次后适应度的平均值曲线图.由图可知，传统SOA收敛速度比较快，当迭代次数大于200以后，适应度基本趋于稳定值0.2，而AUS-SOA的适应度在迭代次数至200时明显小于0.1，至500时，小于0.04.在迭代次数为35时，传统SOA和AUS-SOA的适应度值相同，结合表5可知，传统SOA的运行时间比AUS-SOA少了4.85 s，短期内的搜索效率略高于AUS-SOA.当传统SOA和AUS-SOA的适应度值为0.2时，AUS-SOA的运行时间比传统SOA减少34.68 s以上，显然AUS-SOA在很大程度上保留了SOA局部搜索的高效性，同时迅速提高了SOA的全局搜索能力.

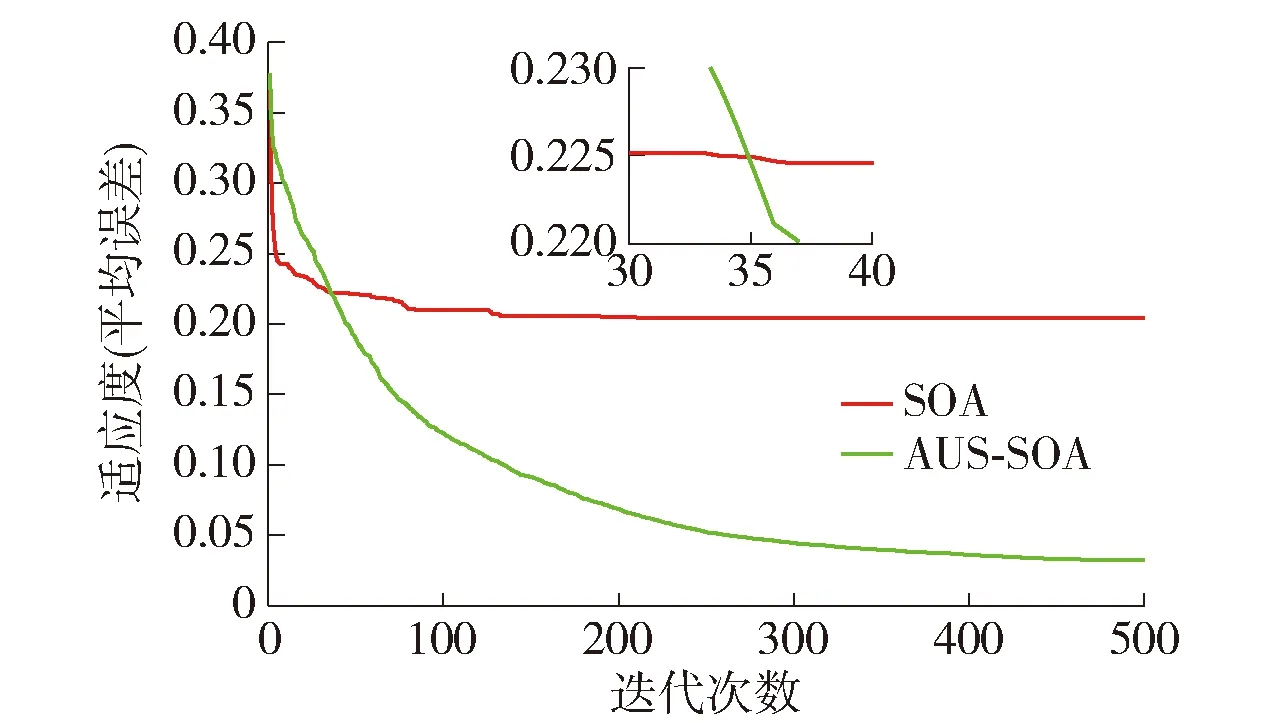
图3 SOA和AUS-SOA的对比Fig.3 Comparison of SOA and AUS-SOA

表5 SOA和AUS-SOA的运行时间对比

3.4 测试集的故障诊断结果分析

本文给出了约减后的测试集基于BRB的油浸式变压器故障诊断模型，在PSO、SOA和AUS-SOA下的故障诊断结果(取5次实验的平均值)；另外，本文还给出了约减后的测试集在支持向量机下的诊断结果以及约减前的测试集在AUS-SOA、IEC(International Electrotechnical Commission)三比值法和粗糙集[24]3种方法下的诊断结果(见表6).

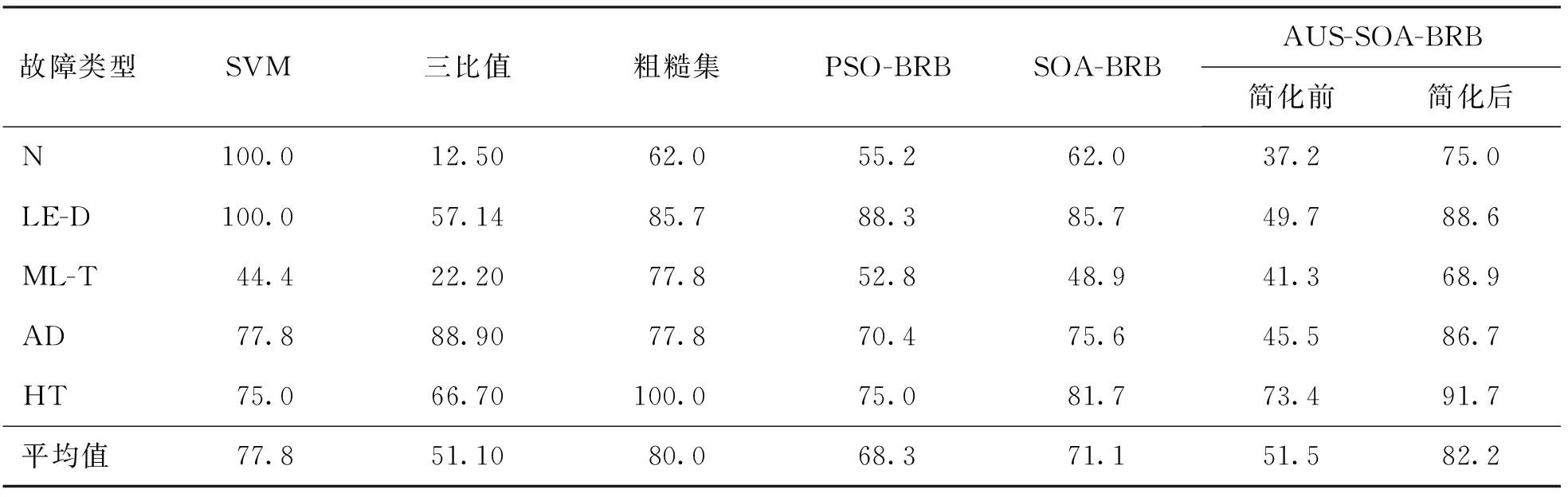
表6 测试集诊断结果的正确率

由测试数据集的诊断结果可知，SVM、IEC三比值法、PSO-BRB和SOA-BRB诊断结果的正确率皆低于80%，这是因为SVM具有较强的泛化能力，对大样本数据的分类效果不够好，而IEC三比值法是由典型事故统计分析得到的，对复杂样本数据的处理不够可靠.PSO-BRB和SOA-BRB对变压器故障诊断的正确率为70%左右，说明SOA-BRB对变压器故障诊断具有可行性且SOA比PSO更加有效，但SOA和PSO的性能有待进一步提高.粗糙集和简化后的AUS-SOA-BRB对变压器故障诊断的正确率都在80%以上，说明粗糙集及AUS-SOA-BRB对变压器故障诊断的有效性.模型简化后明显提高了AUS-SOA-BRB对变压器故障诊断的正确率.此外，本文提出的AUS明显提高了SOA-BRB模型对油浸式变压器故障诊断的准确度，并且AUS-SOA-BRB诊断结果的正确率最高.

由上述实验结果分析可知，简化后的BRB专家系统模型针对油浸式变压器故障诊断问题具有更强的适应性.此外，与传统的数学规划模型相比，智能优化算法对非线性非凸优化问题具有较强的处理能力.进一步地，根据SOA算法的搜索特性，选择更为合理的算法改进策略AUS可以有效提高算法的运算效果和搜索精度.