单组分液滴在快速降压环境下传热传质过程研究

2021-09-14杜小泽韦佳吟吴江波

西华大学学报（自然科学版） 2021年5期

杜小泽，韦佳吟，吴江波

（兰州理工大学能源与动力工程学院，甘肃兰州 730050）

液滴的相变过程涉及物性的变化和气液界面的移动，是复杂的多相传热传质问题。目前所见文献大多是对碳氢燃料液滴在高温环境下的蒸发，以及含有易挥发性成分的液滴在常压环境下的蒸发的研究。费舒波等[1]研究了单组分机油液滴在高温高压环境下的蒸发过程，分析了异辛烷和长链烷烃的蒸发异同及其影响因素对体积膨胀的影响，包括环境压力、环境温度、液滴初始半径等。部分学者针对燃料液滴从亚临界到超临界的蒸发和转变过程，以及转变所需时间和压力、环境温度、初始液滴直径等因素的变化进行研究[2]。对于低压环境下燃料液滴的蒸发过程也有学者推导出液滴直径随时间变化的理论模型，并通过实验分析了环境压力对液滴汽化和蒸发的双重影响[3]。此外，Chen等[4]认为在液氢液滴蒸发过程中，存在一个临界半径使得辐射热和传导热相等，且随着液滴半径的减小辐射热所占比例也逐渐减小，传导热所占比例增大。Rybdylova 等[5]构建了考虑再循环时液滴中组分质量扩散规律的新模型，使用FLUENT 软件绘制了乙醇和丙酮液滴的温度、表面质量分数的变化及液滴沿其径向的变化，将结果与之前开发的模型预测结果比对显示误差较小，故新模型可应用于更多实际场合。

液滴在降压环境下的蒸发过程即闪蒸过程，是指饱和液滴的环境压力突然降低，导致部分显热以汽化潜热的形式被吸收，使得液滴剧烈相变成为蒸气。对于航空航天方面，低温闪蒸喷雾能够有效解决极端散热问题。Zhou 等[6−7]研究了阻力对气流中运动的单组分制冷剂液滴的影响，观察了喷雾液滴在运动过程中直径、温度和速度的变化。此外，还开发了单个液滴蒸发的计算模型，研究了在气流中单个运动液滴的蒸发过程，液滴直径及运动速度随喷射距离的变化。后续研究又在CFD 模拟的基础上考虑液滴表面与环境之间的传热传质作用，建立了液滴蒸发耦合模型[8]。在工业脱盐、海水淡化方面，崔婧格等[9]研究了低压环境下多组分的海水液滴蒸发的变化及环境压力、温度对液滴中心温度的影响。刘琰等[10]讨论了不同浓度的盐水液滴在蒸发时的形态变化及温度变化。当盐水浓度较高时，液滴蒸发过程会存在析盐现象。有国内学者研究了有无析盐过程对液滴中心温度的影响，分析了不同条件对液滴温度的影响以及不同液滴浓度下盐水液滴的相变过程[11]。Liu 等[12]针对不同浓度乙醇和乙酸液滴建立了液滴蒸发过程的数学模型。该模型求解了一维热传导方程和组分扩散方程，得到了液滴内部的温度分布和浓度分布，引入活度系数来模拟液滴表面的蒸汽分压。除了悬挂液滴的研究，也有学者对壁面上固着液滴的蒸发过程进行研究，认为蒸发过程可分为非等温扩散蒸发阶段和准等温蒸发阶段，且除了扩散传递和分子导热以外，汽-气对流也起着很重要的作用，观察了蒸发过程中液滴水蒸气分压随时间的变化[13−14]。Lee 等[15]提出了一种含界面蒸发质量通量的优化模型来模拟液滴蒸发，并采用无条件梯度稳定格式对控制方程进行离散，研究了液滴与固体表面的接触角对液滴蒸发过程形态和尺寸变化的影响。

目前，学者们对于降压环境下单组分液滴的研究主要是基于球形蒸发理论进行数值模拟，即假定蒸发过程中液滴始终维持球形，但现有的蒸发模型无法体现蒸发过程中气液界面、温度场以及蒸汽组分等的分布和变化，因此基于体积流体的VOF方法显得格外重要。该方法可以对气液界面进行跟踪，动态显示蒸发过程中液滴形态的变化。李金达[16]考虑了气液界面相分数的变化，基于VOF 方法建立了新的液滴蒸发模型，研究了热电偶丝导热对单组分燃料液滴蒸发特性的影响及蒸发过程中气液组分的变化。Saufi 等[17]忽略了表面张力并向液滴内部引入向心力，添加了液滴蒸发过程中的内部场，建立了液滴蒸发的多维求解器，结果表明这种求解器的模拟结果在自然对流、强迫对流、微重力工况下与实验数据都非常吻合。Scapin等[18]也是基于体积流体VOF 方法，提出了蒸发过程两相界面解析模拟的数值方法，这种方法能够更为精确地模拟两相流的蒸发流动过程。

物性、传热传质等因素的影响使得液滴蒸发问题格外复杂，因此建立完善的单组分液滴蒸发模型是研究不同种类液滴蒸发的基础。本文基于VOF 方法建立了纯水液滴的蒸发模型，采用开源软件OpenFOAM 分析单个纯水液滴在快速降压环境下相变过程的形态变化和液滴内部速度场、蒸汽分布随时间的变化特征，研究了最终环境压力、初始液滴直径等因素对液滴蒸发速率及液滴中心温度的影响。

1 液滴蒸发的数学模型

1.1 控制方程

本文选择一种多相、支持跨相质量传递和热传递的求解器，基于VOF 方法捕捉气液界面。在求解控制方程的过程中，将气液看作一相，即只求解一组N-S 方程，但热物理参数及相模型的种类必须按照气液两相的不同选择相应的参数。

液相体积分数的运输方程如下：

此时在计算过程中密度等物理参数不再是常数，而是相分数的函数，界面上的值需要根据不断更新，相关公式如下：

式中：下标l 表示液相参数；g 表示气相参数。

存在重力及源项时，不可溶多相介质的动量方程如下：

式中：σ 是表面张力系数；κ 表示界面处的曲率，其值为

在多相流求解器中，定义prgh=p−ρg·h，则式(4)可写成

由于在VOF 方法中气液两相看作一种流体，所以能量守恒方程可写成如下形式：

式中：k、cp分别表示导热系数和定压比热容；L表示汽化潜热；方程右侧第二项表示汽化潜热及由两相之间比热的差异引起的热量变化。

气体组分方程如下：

1.2 蒸发模型

由于蒸发过程受环境压力变化的影响，模型需要考虑压力对界面蒸气质量分数的影响，因此选用KineticGasEvaporation 模型。该模型基于气体动力学理论，考虑了赫兹克努森公式，即假设液体和蒸气处于平衡状态，给出了基于动力学理论时气液界面的蒸发凝结通量。

式中：c为调节系数；M为相对分子质量；R为通用气体常数；Tact为饱和温度；p为蒸汽分压；psat为饱和压力。

其中饱和条件下压力与温度的关系通过Clapeyron-Clausius 方程表示为[20]

式中 νg、νl分别表示蒸汽、液体密度的倒数。

综上，式(10)可写成以下形式[21]：

2 模型建立

2.1 液滴模型

本文针对纯水液滴在快速降压环境下的蒸发过程建立数值模型，研究在蒸发过程中液滴的形态变化及液滴内部温度场的变化。首先做如下假设：1）液滴轴对称蒸发；2）将气体看作不可压缩理想气体；3）液滴蒸发过程处于准稳态；4）忽略液滴与环境间的热辐射；5）所有流体均为层流。

2.2 计算网格

计算模型采用三维笛卡尔坐标系，在求解二维算例时第三个方向的厚度设置以不影响求解为原则。本文建立二维结构化计算网格，取直径为40 mm 的圆形计算域，如图1 所示，直径为2 mm 的液滴悬挂在直径为0.1 mm 的热电偶节点上。为减少计算量，假设液滴球对称蒸发，将求解域简化为一半，设置左侧为对称面。为使蒸发界面及液滴内部场更清晰，在中心液滴区域内设置较密网格，并为相分数指定一个非均匀的初始液相场和温度场，如图2 所示，在液滴界面内设置相分数α 为1，液滴周围空气相分数为0，设置初始液滴温度为17 ℃（即290 k）。

图1 计算网格及尺寸

图2 初始液相场和温度场

2.3 离散方法和求解方法

离散格式的选择中，对时间项选择一阶隐式欧拉格式，梯度项使用高斯积分计算，但具体的体心到面心的离散使用中心差分（即线性插分）格式，主要用于计算面通量。针对动量方程和能量方程中的对流项选用二阶的高斯线性迎风格式以实现良好的精度。这种离散格式基于高斯积分和迎风格式但比线性插分在数值上得到的结果更好，但需要指定相应的速度和温度梯度。由于中心差分格式在纯对流的情况下相对不稳定，因此对于气液相体积分数运输方程选用vanLeer 格式，拉普拉斯项选用正交修正后的高斯线性插分格式。

控制方程的求解过程根据不同的方程编写相应的对称或非对称矩阵求解器。时间导数以及拉普拉斯项的离散为对称矩阵，对流项的引入会导致矩阵非对称，因此相体积分数场和温度场的方程使用非对称共轭求解器PBiCG 来求解。压力场选择用于对称矩阵的PCG 求解器，速度场选择对称高斯赛德尔光顺求解器 smoothSolver。速度–压力的耦合方程选用PISO 算法，其特点是在每个迭代步长内先求解压力方程以保证质量守恒，然后再附加速度修正来求解动量方程，最后对所有方程进行松弛，保证矩阵的对角占优。

3 实验系统及方法

3.1 实验系统

实验利用真空泵降低测试罐内的压力，研究液滴在快速降压环境下的蒸发特性。如图3 所示，将液滴悬挂在热电偶节点上进行测温。实验系统分为测试系统、真空系统、图像部分以及数据采集系统。其中测试系统由测试罐、热电偶、压力传感器以及球阀组成；真空系统由真空泵、真空罐、相应的连接管道和阀门组成；数据采集系统采用KEITHLEY 公司的2700 数据采集系统，以获得液滴的中心温度以及测试罐内压力的变化；图像部分由高速摄像机和红外热像仪组成，以捕获液滴形态变化及液滴表面温度。

图3 液滴降压环境下蒸发过程实验系统图

3.2 实验方法

实验开始前需检查设备状况，确保设备及测试罐气密性良好。具体实验步骤如下：打开阀门10，通过真空泵11 对真空罐9 进行抽气；打开阀门3 关闭阀门6，利用压力传感器实时获取真空罐中的压力数值；完成抽气后，打开阀门6 关闭阀门3，读取测试罐内的压力；实验开始时打开连接真空罐和测试罐的球阀8 使测试罐尽快降压，压力传感器和热电偶连接在2700 数据采集系统上，再通过计算机读取数据；摄像机4 和红外热像仪7 分别位于测试罐两侧以观察液滴的形态变化和表面温度。

4 结果与讨论

4.1 验证模拟结果

图4 对比了实验结果[11]和数值模型中液滴中心温度的变化，验证了数值模型的有效性。图4（a）模拟条件设置为最终环境压力为1500 Pa，初始环境温度为20 ℃，液滴温度为17 ℃，液滴初始直径为1.5 mm。可以看出模拟值与实验结果吻合较好。随着测试罐内压力的降低，液滴温度超过饱和温度，因此液滴表面大量吸收液滴内部的热量而快速蒸发，中心温度快速降低，在4 s 之后蒸发速度逐渐稳定，故液滴中心温度趋于平缓。图4（b）模拟条件设置为初始环境压力为840 Pa，环境温度为20 ℃，液滴温度为16 ℃，液滴初始直径为1 mm。由于酒精的挥发性较强，液滴的饱和温度和沸点温度都较低，因此在降压过程中液滴中心温度降低的速率更快，所能到达的最低温度也越低。

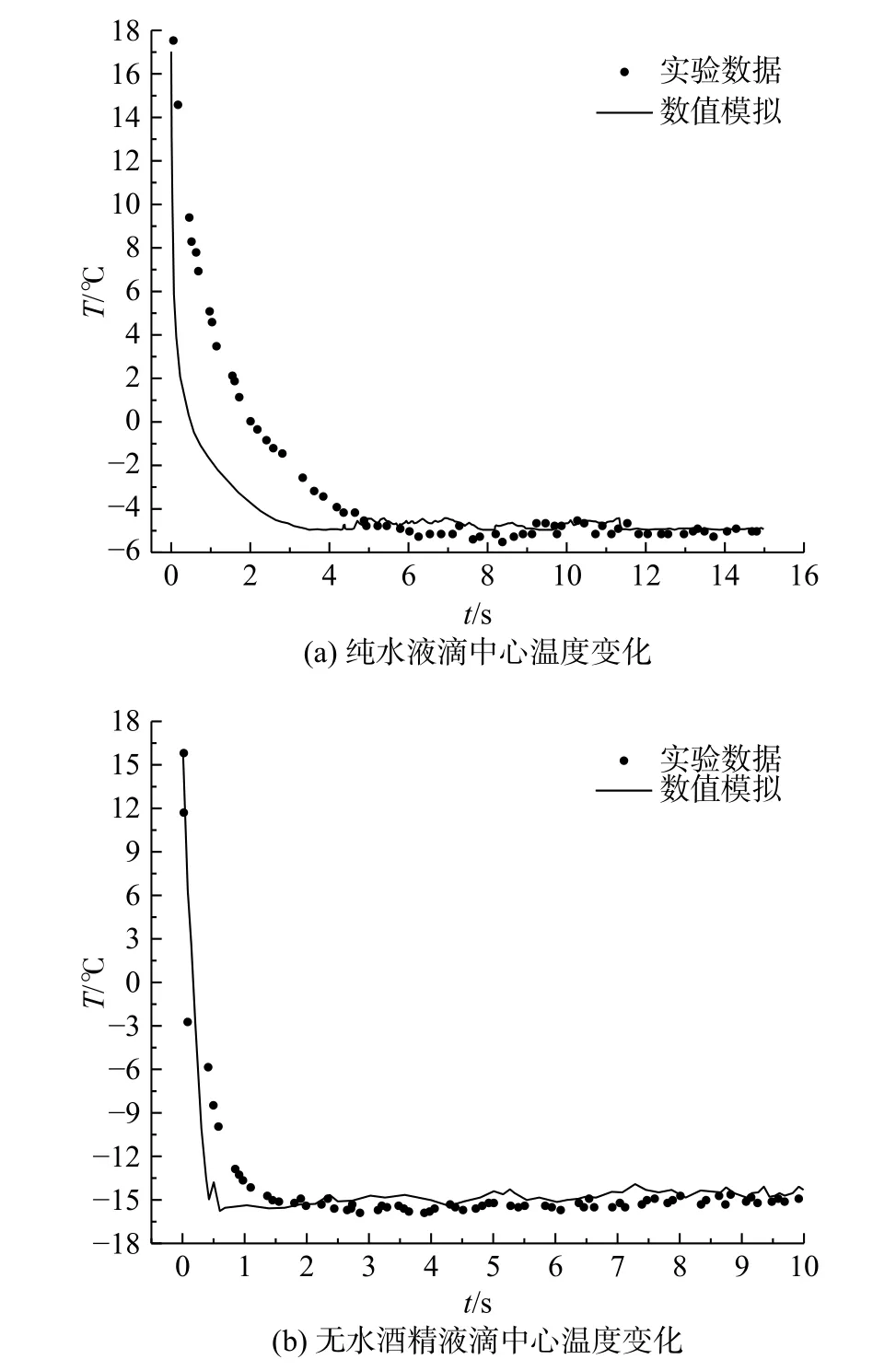
图4 模拟与实验结果对照图

在降压初始阶段，模拟结果与实验所得液滴中心温度下降速度存在误差，是因为在开启阀门后，由于管道等因素影响导致压力并不是立即降低，而是稍有延迟，所以实验结果中液滴中心温度的降低速度较为缓慢。

4.2 液滴蒸发特性

图5 显示了蒸发过程中液滴形态随时间的变化。蒸发初期，液滴中心悬挂在热电偶节点上，随着环境压力的降低，引起流场内速度变化，导致在蒸发过程中液滴并不能持续维持中心悬挂在热电偶节点上，且随着压力的变化表面形态也在不断变化，也没有维持球形形态。

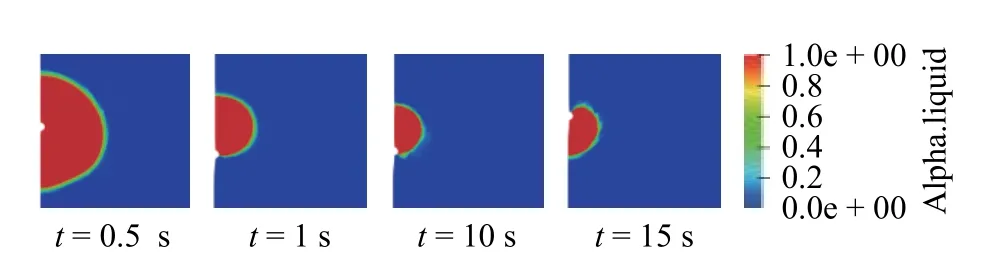
图5 液滴蒸发过程形态变化

图6 显示了蒸发过程中液滴内部及环境中的速度场随时间的变化。t=0.5 s 时可以看到，初始降压阶段，压力变化大，液滴蒸发速度较快，此时，液滴大量吸收内部热量而蒸发，液滴内部水分子及气液边界处的蒸汽分子的动能较大，向四周做无规则运动，因此液滴内部及边界处流体速度变化较为明显。随着蒸发过程的稳定，分子动能逐渐减小，环境中空气的流速和液滴内部流速也逐渐稳定。

图6 液滴蒸发过程速度场

图7 显示了液滴蒸发过程环境中的无量纲蒸汽浓度的分布。蒸发初期产生的蒸汽凝聚在液滴周围，环境中还是以空气为主，随着液滴的蒸发和环境中气流的运动，气化后的蒸汽混入周围的空气中，并随着空气由中心向四周扩散，到t=10 s 后蒸汽的分布逐渐稳定，且部分蒸汽随空气从出口流出。

图7 蒸发过程无量纲蒸气浓度分布

4.3 影响液滴中心温度的因素

最终环境压力对液滴中心温度的影响如图8所示。在其他条件相同时，数值模拟了最终压力分别降低至1200、1500、2 000 Pa 时液滴中心温度随时间的变化。通过曲线可以看出，由于环境压力降低，导致对应压力下液滴的饱和温度降低，因此液滴中心最低温度随着最终压力的降低而降低，且最终环境压力越低，在0～2 s 内液滴中心温度变化的速率越大，所达到的最低温度也越低。

图8 最终压力对液滴中心温度的影响

初始液滴温度对中心温度的影响如图9 所示。控制其他变量相同，分别设定液滴初始温度为17 ℃和27 ℃。随着液滴初始温度的升高，液滴中心达到最低温度后回升的速率越快。两种条件下液滴中心都是在4 s 左右达到最低点，但初始温度为17 ℃时，约在30 s 左右中心温度开始回升，而初始温度为27 ℃时，由于液滴内能较大，可供液滴表面蒸发的潜热较多，因此液滴蒸发速率较快，中心温度到12 s 左右开始回升。由曲线可以看出，在液滴蒸发至40 s 时，由于蒸发速率不同，热点偶节点附近蒸气组分浓度不同，导致液滴中心温度回升到的温度差高达8 ℃左右。

图9 液滴初始温度对中心温度的影响

4.4 影响液滴蒸发速率的因素

最终环境压力对蒸发速率的影响如图10 所示。在降压蒸发过程中，液滴并不一直维持球形，故无法用传统的无量纲直径表示液滴蒸发速率。这里采用无量纲相分数判断液滴是否完全蒸发，其中纵轴alpha.liquid 表示液滴中心的液相分数，当其值为0 时，表示液滴已蒸发完成。分别设定最终压力为1200、1500、2 000 Pa。由图可以得知，液滴初始时刻蒸发速率随着环境压力的降低而增大。当环境压力降低至2 000 Pa 时，液滴在0～2 s 内迅速蒸发，在2～10 s 内蒸发较为平稳。这是因为随着环境压力的稳定，环境中气流流速变化减小，因此相较初始阶段此时液滴蒸发速率减慢，且液滴完全蒸发所需时间明显较最终压力为1200 Pa 和1500 Pa 长，约为52 s 左右。这是由于最终环境压力较高时，液滴蒸发所对应的饱和温度相对较高，液滴表面蒸发时需要从液滴中心吸收更多的热能，因此相同环境温度下液滴蒸发速率更慢。

图10 最终环境压力对蒸发速率的影响

初始液滴直径对蒸发速率的影响如图11 所示。数值模拟了液滴初始直径分别为1、1.5、2 mm 时液滴的蒸发速率。由3 条曲线可以看出：初始直径分别为2、1.5、1 mm 时，液滴完全蒸发所需时间分别约为37、27、23 s，液滴完全蒸发需要的时间随着初始液滴直径的减小而减小；当液滴直径小于1.5 mm 时，初始液滴大小对蒸发速率的影响可忽略；当液滴直径大于1.5 mm 时，直径对蒸发速率的影响较大。

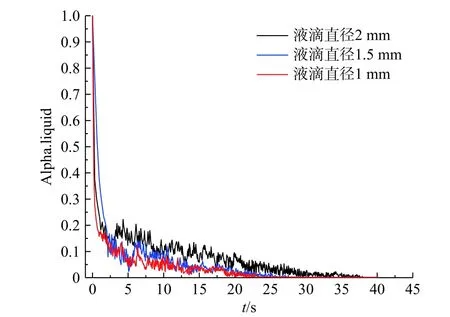
图11 初始液滴直径对蒸发速率的影响

初始液滴温度对蒸发速率的影响如图12 所示。控制其他条件不变，分别设定液滴初始温度为17 ℃和27 ℃。随着液滴初始温度的升高其完全蒸发所需时间明显减小。从图12 可以看出，初始温度为17 ℃时，液滴完全蒸发大约需要37 s，而初始温度升高10 ℃后，其完全蒸发仅需23 s。这是由于初始温度较高时液滴内部所储存的热量更多，所以蒸发时速度更快。