考虑油膜力影响的船舶轴系热态校中计算模型

2021-09-13金尚崇孟文杰温小飞陈宁宁

广东造船 2021年4期

金尚崇孟文杰温小飞陈宁宁

摘要：针对船舶轴系校中计算结果在热态工况与实际工况之间存在的相符性问题，进一步探讨在传统热态轴承变位计算基础上，考虑增加轴系轴承油膜力影响因素，建立基于油膜动力学的船舶推进轴系热态校中计算模型。通过实例校中计算和数值对比分析，结果表明：在热态工况，考虑油膜动力学影响的船舶轴系校中计算结果更能反映船舶轴系实际运行状态。

关键词：船舶轴系;轴系校中;热态;轴承负荷;油膜力

中图分类号：U664.21 文献标志码：A

Abstracts： In view of the consistency between the calculation results of ship shafting alignment in hot working conditions and the actual working conditions， this paper establishes the hot condition alignment calculation model of ship propulsion shafting based on the traditional hot condition bearing displacement calculation and considering the influence of the oil film force of shafting bearing. Through the alignment calculation and numerical comparison analysis， the results show that the ship shafting alignment calculation results considering the influence of oil film dynamics can better reflect the actual operation state of ship shafting in hot condition.

Key words： Ship shafting; Shafting alignment; Hot condition;Bearing load; Oil film force

1 前言

船舶軸系校中计算，主要用于设计阶段、安装状态、运行状态的评价。船舶轴系校中质量好坏受到诸多因素影响，包含静态因素和动态因素。近几年来，在静态因素影响研究方面，严由贵等[1]研究了耐压艇内液舱不对称布置对轴系校中特性的影响;李泽远等[2]提出一种考虑船体变形的轴系动态校中算法;而在动态影响因素研究方面，刘金林等[3]研究了螺旋桨水动力的影响;蔡保刚等[4]在假设的稳态工况下的轴系校中和轴承稳态负荷计算方法;张阳阳等[5]通过研究轴承变位对轴承油膜特性的影响，建立了校中状态对轴系振动传递特性的影响关系;王鼎等[6]探索了不同校中因素下的轴系纵横耦合振动特性;杨红军等[7～9]研究了轴系校中计算中尾管后轴承Hertz接触模型的非线性建模方法，模拟了各个轴承和轴颈接触形态，计算了艉管后轴承油膜支反力;黄杰雄等[10]研究了多种动态因素影响耦合关系，并开发了专门计算系统。其中，船舶轴系尾管后轴承润滑油膜特性，作为影响轴系校中动态因素之一[11]，在船舶轴系校中计算模型中考虑油膜力影响将对轴系校中准确度提升与系统运行安全保障方面，具有显著的工程意义。

2 轴系校中计算模型

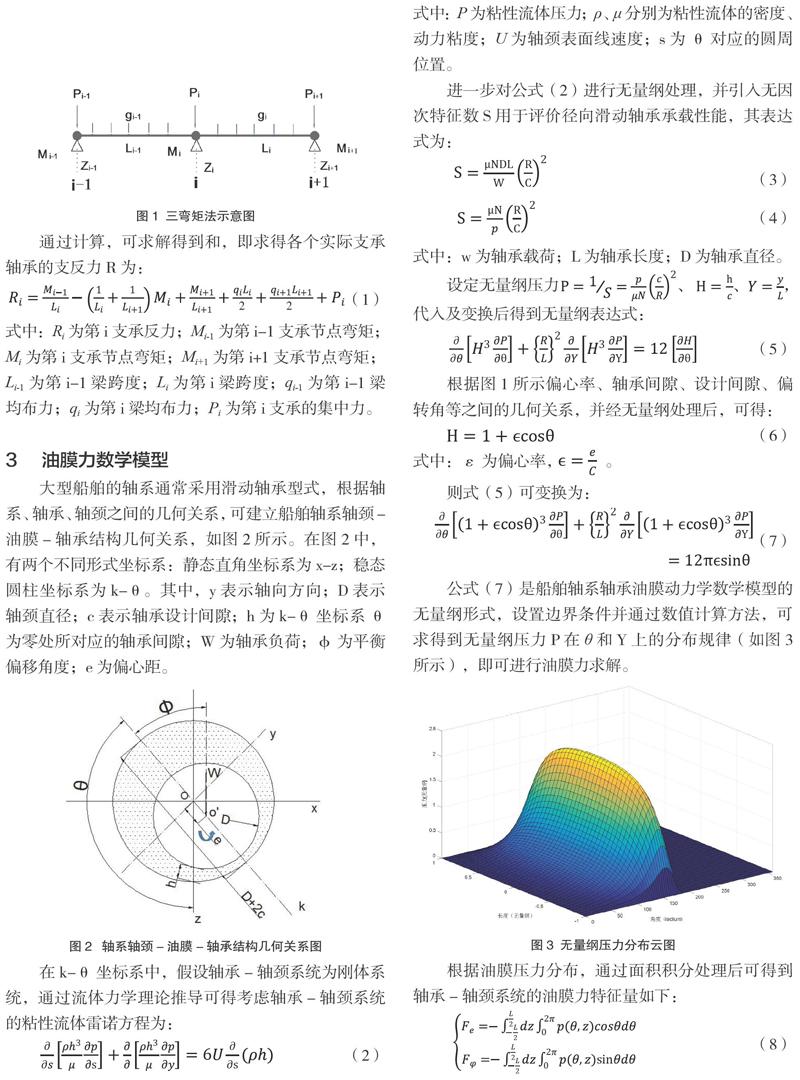
船舶轴系校中计算模型，一般可分为：传递矩阵模型;三弯矩模型;有限元模型等。其中，三弯矩模型以超不静定梁理论为基础，以铰链连接形式处理每个中间支座上方的梁结构形式，即在任一支座两侧梁截面具有弯矩大小相等、方向相反，与其对应的位移即为两侧截面相对转角等特征，如图1所示。图1中：P为集中力;g为均布力;L为单元长度;M为弯矩;Z为轴承变位值;i表示节点序号。

通过计算，可求解得到和，即求得各个实际支承轴承的支反力R为：

式中：为第i支承反力;为第i-1支承节点弯矩;为第i支承节点弯矩;为第i+1支承节点弯矩;为第i-1梁跨度;为第i梁跨度;为第i-1梁均布力;为第i梁均布力;为第i支承的集中力。

3 油膜力数学模型

大型船舶的轴系通常采用滑动轴承型式，根据轴系、轴承、轴颈之间的几何关系，可建立船舶轴系轴颈-油膜-轴承结构几何关系，如图2所示。在图2中，有两个不同形式坐标系：静态直角坐标系为;稳态圆柱坐标系为。其中，y表示轴向方向;D表示轴颈直径;c表示轴承设计间隙;h为k-坐标系为零处所对应的轴承间隙;W为轴承负荷;为平衡偏移角度;e为偏心距。

在坐标系中，假设轴承-轴颈系统为刚体系统，通过流体力学理论推导可得考虑轴承-轴颈系统的粘性流体雷诺方程为：

进一步对公式（2）进行无量纲处理，并引入无因次特征数S用于评价径向滑动轴承承载性能，其表达式为：

根据图1所示偏心率、轴承间隙、设计间隙、偏转角等之间的几何关系，并经无量纲处理后，可得：

则式（5）可变换为

公式（7）是船舶轴系轴承油膜动力学数学模型的无量纲形式，设置边界条件并通过数值计算方法，即可求得到无量纲压力P在和Y上的分布规律（如图3所示），即可进行油膜力求解。

4 耦合油膜力的轴系热态校中计算模型

假设以船舶轴系静止状态时的轴颈位置为基准（即其值为零），在船舶轴系稳定运行时（即油膜力与轴承负荷大小相等、方向相反），第i个轴系轴颈中心位置为，用矩阵表示为，则船舶轴系轴承负荷为：

5 实例分析

以某64000DWT散货船轴系为例，计算在考虑油膜力影响时其在热态工况下轴系校中情况。计算涉及船舶轴系几何尺寸及长细比等参数，如表1所示：

船舶轴系轴承负荷计算不仅需要轴颈、轴承、轴承间隙等几何尺寸，还需要输入轴承润滑油物性参数、工作环境参数等。滑油物性参数一般有粘度-温度特性曲线，提取20℃～100℃范围内的具体;滑油密度以15℃时密度为输入量;船舶轴系工作温度设置为。

计算数据整理后，可得到热态工况下的轴系轴承负荷变化曲线（图4）和轴系轴颈位置变化曲线（图5）。

从图4中可以看出，8个轴承所对应的轴承负荷均随着转速变化而变化，但是具体变化特征存在差异性： 1号轴承负荷略有下降;中间轴承负荷逐渐增大;主轴承负荷微小波动;

从图5中可以看出，8个轴系轴颈位置均随着转速升高而增大，具有相似的变化趋势;但在轴系轴颈位置大小及其变化速率等方面存在较大差异。这体现了热态工况下轴系轴承负荷重新分配的特点，且轴颈位置、轴承负荷、油膜力之间具有耦合关系。

进一步选取尾轴承负荷和中间轴承负荷比较，对两种不同计算模型的计算结果进行对比分析，详见图6。从图6中可以明显看出：在油膜力作用下，中间轴承和尾轴承负荷均发生了变化，而无油膜力影响时其值均保持不变。在轴系实际运行过程中，油膜力作用是必然存在的，因此考虑油膜力影响的计算模型能更准确的反映船舶轴系热态工况，在轴系稳定运行阶段轴承负荷会进行重新分配和平衡。

6 结论

考虑油膜力影响的船舶轴系热态校中计算模型，其计算结果表明：船舶轴系轴承负荷、轴系状态不是始终保持不变的，而是随着转速变化而改变，其结果更能反映船舶轴系实际运行状态。本计算模型可用于船舶轴系稳定运行状态分析。

参考文献

[1]严由贵，卜文俊，徐荣武.艇体变形对轴系校中的影响[J].船舶工程，2019，41（11）：41-44+88.

[2]李泽远，汪骥，刘玉君.考虑船体变形的轴系动态校中算法[J].船舶工程，2018，40（10）：59-63.

[3]刘金林，赖国军，尹红升，曾凡明，周瑞平，雷俊松.舰艇电力推进轴系多学科优化设计研究[J].中国造船，2019，60（02）：150-163.

[4]蔡保刚. 船舶推进轴系轴承稳态负荷计算方法与试验研究[D].浙江海洋大学学报，2019.

[5]张阳阳，所俊.校中状态对轴系横向振动传递特性影响研究[J].舰船科学技术，2020，42（11）：65-70.

[6]王鼎. 基于軸承动态润滑特性的船舶推进轴系振动特性研究[D].华中科技大学学报，2019.

[7]杨红军，李俊，刘镇剑.基于Hertz弹性接触的船舶推进轴系非线性校中计算[J].船舶力学，2019，23（02）：218-226.

[8]杨红军，卢菲，车驰东.基于尾管后轴承分段弹性接触的船舶推进轴系校中计算[J].上海交通大学学报，2018，52（06）：681-686.

[9]杨红军，王文中，李俊，曹信来.考虑艉管后轴承油膜支承力的轴系校中计算[J].中国造船，2018，59（01）：142-150.